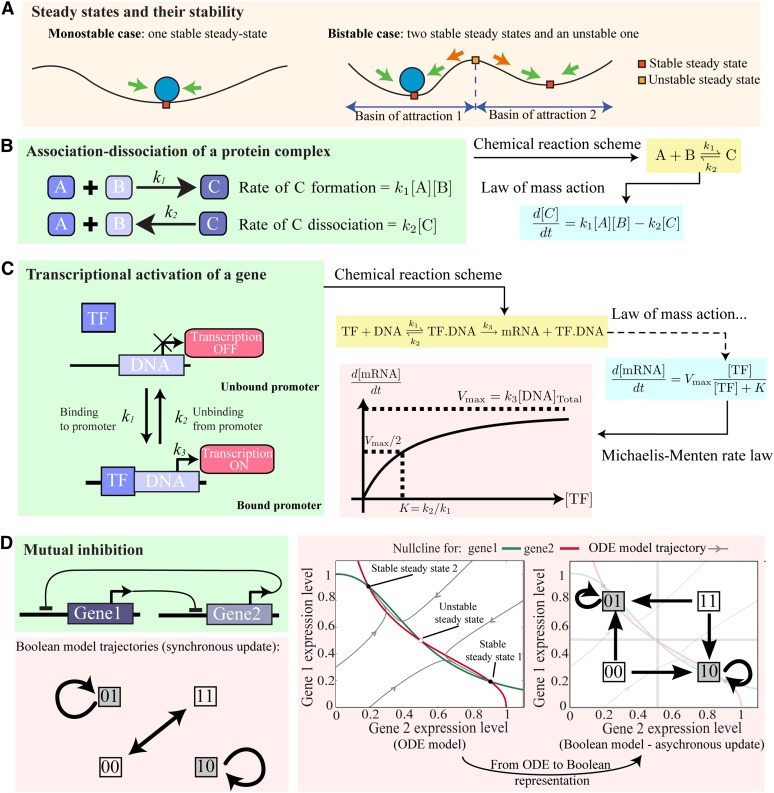
Figure 1.

Introduction to Dynamical Models of Small Networks.

(A) Cartoon illustrating key properties of a dynamical model.

(B) Mass action model for the association and dissociation of two proteins. These can be written in terms of a chemical reaction scheme. The law of mass action dictates how the rate of formation and dissociation depend on the concentration of the reactants. From this an ODE can be formulated.

(C) A Michaelis-Menten model of gene expression. The model can be formulated by applying the law of mass action to the chemical reaction scheme depicted. TF, transcription factor.

(D) The mutual inhibition feedback loop. Both Boolean- and ODE-based models (right panel) are bistable (for certain parameter values) and have analogous steady states. However, in the Boolean model, transitions between the states depend on which update method is used (cf. right panel and bottom panel).