Numerical solutions of the γ-index in two and three dimensions

Abstract

The γ-index is used routinely to establish correspondence between two dose distributions. The definition of the γ-index can be written with a single equation but solving this equation at millions of points is computationally expensive, especially in three dimensions. Our goal is to extend the vector-equation method in Bakai et al [1] to higher order for better accuracy and, as important, to determine the magnitude of accuracy in a higher order solution. We construct a numerical framework for calculating the γ-index in two and three dimensions and present an efficient method for calculating the γ-index with 0^th, 1^st, and 2^nd-order methods using tricubic spline interpolation. For an intensity modulated radiation therapy example with 1.78 × 10⁶ voxels the 0^th-order, 1^st-order, 1^st-order iterations and semi 2^nd-order methods calculate the 3-dimensional γ-index in 1.5, 4.7, 34.7, and 35.6 s with 36.7%, 1.1%, 0.2% and 0.8% accuracy, respectively. The accuracy of linear interpolation with this example is 1.0%. We present efficient numerical methods for calculating the 3-dimensional γ-index with tricubic spline interpolation. The 1^st-order method with iterations is the most accurate and fastest choice of the numerical methods if the dose distributions may have large second-order gradients. Furthermore, the difference between iterations can be used to determine the accuracy of the method.

1. Introduction

The γ-index criterion of Low 1998 [2] is often used in radiation therapy to evaluate the correspondence between two dose distributions, e.g. a measured dose distribution D₀(ρ⃗₀) and a planned dose distribution D(ρ⃗). This method is commonplace in external beam therapy [3] for commissioning and quality assurance.

The γ(ρ⃗₀) is the minimum point-to-surface distance (PSD) between points on a reference surface and an evaluation surface in an abstract vector space where the first 1, 2 or 3 coordinates represent space and an additional coordinate represents dose. Mathematically, this is given by

$$\gamma ({\overrightarrow{\rho }}_0)=\underset{\overrightarrow{\rho }}{min}\left(\sqrt{\frac{{\mid \overrightarrow{\rho }-{\overrightarrow{\rho }}_0\mid }^2}{\delta {d_0}^2}+\frac{{(D(\overrightarrow{\rho })-D_0({\overrightarrow{\rho }}_0))}^2}{\delta {D_0}^2}}\right),$$ (1)

where ρ⃗ is a spatial vector to a point. The vector notation with an arrow denotes vectors of the spatial coordinates. The selected distance and dose tolerances for the comparison are given by δd₀ and δD₀, respectively.

Correspondence between the two distributions is acceptable when the fraction of points with γ ≤ 1 equals or exceeds a selected pass rate within a region of interest. For example, AAPM Task Group 119 performed a multi-institutional comparison of data from intensity modulated radiation therapy (IMRT) commissioning with a distance/dose tolerance of 3 mm/3%, respectively, with a pass rate of 90% and the region of interest given by either a rectangle or the region with dose >10% of the maximum dose [3].

The 3-dimensional γ-index [4][5] is of special interest, but computationally complex, as treatment plans have margins around the clinical target volume in 3-dimensions and delivery uncertainties exist in 3-dimensions. A 2-dimensional γ-index for a 3-dimensional problem could give false-negative results in planes with steep longitudinal dose gradients that are, in fact, acceptable given the margins.

The minimum PSD in its simplest form is determined by interpolating dose distributions and searching over the interpolated grid for the minimum PSD for different ρ⃗. We call this method “Trial and Error (TAE).” Depuydt et al [6] describe the complexity of the problem and the sensitivity of γ to the pitch of the interpolation grid. Other methods improve on this technique, such as the vector-equation method of Bakai et al [1], the geometric interpretation of Ju et al [4], and the distance transform approach of Chen et al [7].

Bakai et al 2003 [1] use a vector equation to determine the minimum distance between a point and the tangent of the D(ρ⃗) dose surface at ρ⃗₀. Their result, the χ-index, is positive or negative depending on the sign of the dose difference. They calculate the χ-index in 58 × 10³ voxels within 0.2 s (excluding the time for polynomial interpolation of D(ρ⃗) on the ρ⃗₀ grid). Their 3-dimensional example shows the accuracy of the number of points with |χ| ≥ 1 relative to the number of points with γ ≥ 1 is 0.7% in 2 spatial dimensions and 0.3% in 3 spatial dimensions. Nevertheless, the γ-index rather than the χ-index has been the mainstay of dose distribution comparisons in Medical Physics and we explore more accurate numerical techniques in order to be compatible with the existing definition of γ.

Ju et al 2008 [4] subdivide the D(ρ⃗) dose distribution into simplexes and determine the minimum PSD between a point and a simplex by geometric methods. This technique implicitly applies linear interpolation between the D(ρ⃗) grid points and can be applied in 3 spatial dimensions. In 2 spatial coordinates, their method can be visualized by subdividing the dose surface into flat triangles, which are 2-simplexes, and finding the smallest distance between a point and the triangle. To reduce the computation time, they sort the simplexes in order of ascending spatial distance and calculate the minimum PSD to each simplex in turn and terminate the search when the PSD increases with distance. They calculate a 3-dimensional γ-index in 2 × 10⁶ voxels within 2 minutes.

Chen et al 2009 [7] use a distance transform approach, a technique that derives from digital image processing, to build a table of all possible γ-index values for the D(ρ⃗) dose distribution. γ(ρ⃗₀) is subsequently determined by performing a table lookup for each point in the D₀(ρ⃗₀) distribution. Only the D(ρ⃗) dose distribution is used for the construction of the table and, in this step, D(ρ⃗) is interpolated and “digitized”, i.e. the value for dose at each grid point can be one of only M discrete values. Constructing the table is the most demanding step, for example, the method requires 16 s to construct the table and 20 ms for the table look-up for a 2-dimensional calculation with 400×400 grid points [7]. While no results have been reported for a 3-dimensional computation, their method is feasible in 3-dimensions.

We routinely use a 3-dimensional γ-index calculation for comparing one distribution from treatment planning and the other from measurement or a stand alone dose calculation such as Monte Carlo. The method from Bakai [1] is fast and suitable for our needs except that there is no indication of the accuracy of the χ-index results. Our motivation for developing numerical methods is to extend the fast and elegant method of Bakai to higher order to have quantitative information on the accuracy.

In this work, γ(ρ⃗₀) in Eq. 1 is reformulated as a set of coupled differential equations (Eq. 5), the solution of which yields the γ index through Eq. 6. These equations can be solved to arbitrary order, so the method is general and does not rely on linear interpolation of the dose between voxels. Higher order methods can be applied to yield better accuracy and indicate the uncertainty in the calculations. Multiple numerical methods are developed, to 0^th, 1^st and 2^nd-order, in Sec. 2 and are compared in Sec. 4.6.

2. Methods

The numerical methods for solving the γ-index calculate: the derivatives of the D(ρ⃗) dose distribution at grid points by central finite difference; function values and gradients between grid points by interpolation; a coupled partial differential equation to n^th order in the Taylor series expansion giving ρ⃗ at minimum PSD; and, D(ρ⃗) at the solution point by either re-using the Taylor series expansion or interpolation.

2.1. The PSD problem as a coupled differential equation

The calculations for γ (ρ⃗₀) are simplified with a change in variables. For the voxel at ρ⃗₀, we define the unit-less spatial vector

$$\overrightarrow{r}\equiv (x,y,z)\equiv \frac{\overrightarrow{\rho }-{\overrightarrow{\rho }}_0}{\delta d_0},$$ (2)

and the unitless dose variable

$$f(\overrightarrow{r})\equiv \frac{(D(\overrightarrow{\rho })-D_0({\overrightarrow{\rho }}_0))}{\delta D_0}.$$ (3)

The calculations are further simplified by building vectors in the abstract vector space with 1, 2 or 3 spatial coordinates followed by the dose coordinate in bold font. For example, all points on the dose surface in this notation are described by u ≡ (r⃗, f(r⃗)).

Eq. 1 is recast as a differential equation and is solved with the use of numerical methods. The dose distribution D(ρ⃗) must be continuous, i.e. vary smoothly with position. Dose distributions with discontinuities may need TAE or other methods in the spatial region near the discontinuity but remaining region(s) can be calculated using the differential method.

The minima and maxima in the PSD are at the values of r⃗ such that the normal, n, coincides with u (Figure 1). The normal in 3-dimensions is

Figure 1.

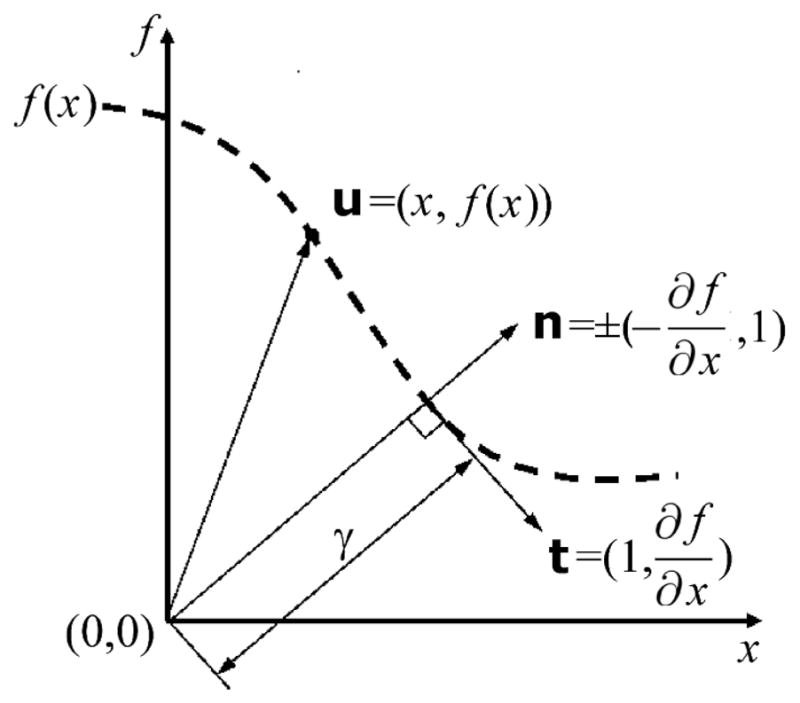
An abstract vector space with 1 unitless spatial coordinate as the horizontal axis, the unitless dose coordinate as the vertical axis and the origin at the location of the reference value for which we wish to find the minimum magnitude of u (Eq. 6). The tangent and normal vectors are t and n, respectively. These vectors are drawn for the value of x where the normal vector passes through the origin and at this position γ = |u|. In three spatial dimensions r⃗ ≡ (x, y, z).

$$\mathbf{n}=\pm (-\nabla f(\overrightarrow{r}),1),$$ (4)

which has the same slope as u at the solution point. By equating the slopes of these two vectors, the PSD problem can be expressed mathematically as finding the value for r⃗ that solves the coupled differential equation

$$\overrightarrow{r}=-f(\overrightarrow{r})\nabla f(\overrightarrow{r}).$$ (5)

Note that f and r are dimensionless, so this equation is not forbidden by analysis of the units. The γ-index follows from

$$\gamma ({\overrightarrow{\rho }}_0)=\mid \mathbf{u}\mid =\sqrt{{\overrightarrow{r}}^2+f{(\overrightarrow{r})}^2},$$ (6)

where u(r⃗, f(r⃗)) is determined from interpolation or Taylor-series expansion at the solution point. The differential equations (Eq. 5) are exact and the only assumption thus far is that f(r⃗) is a continuous function. The differential equations can be solved by numerical methods to yield r⃗ at the minimum PSD.

2.2. Finite difference method

Finite difference methods [8] are used to determine the derivatives of f(r⃗). Throughout this work, we use central finite differences given by

$$\frac{\partial f(\overrightarrow{r})}{\partial x}=\frac{1}{2h}(f(x+h)-f(x-h))+O(h^2\frac{\partial f^3}{\partial x^3}),\text{and}$$ (7)

$$\frac{{\partial }^{2}f(\overrightarrow{r})}{\partial x^2}=\frac{1}{h^2}(f(x+h)-2f(x)+f(x-h))+O(h^2\frac{\partial f^4}{\partial x^4}),$$ (8)

where h is the grid pitch divided by δd₀ and $O(h^2\frac{\partial f^3}{\partial x^3})$ represents the order of terms truncated in this method. Since h is typically ≲ 1, we must rely on higher-order gradients of f(r⃗) to be small to truncate this series. This approximation is most accurate, by Eqs. 2 and 3, when δd₀ is small and/or δD₀ is large. So, one should only apply the finite difference technique to voxels where the ripples in the D(ρ⃗) dose distribution are much smaller than δD₀ and/or the pitch of the ripples are much larger than δd₀.

2.3. Interpolation method

From previous sections, we have the dose distribution f(ρ⃗) and derivatives of the dose distribution at grid points. In this section, the interpolated dose values are denoted by F(r⃗) and interpolated derivatives by ∇F, $\frac{\partial F^2}{\partial x^2}$, etc. The interpolation method must be chosen carefully based on the dose distribution at hand. For example, linear interpolation is suitable if the distribution is smooth and slowly varying such that 2^nd-order derivatives can be ignored.

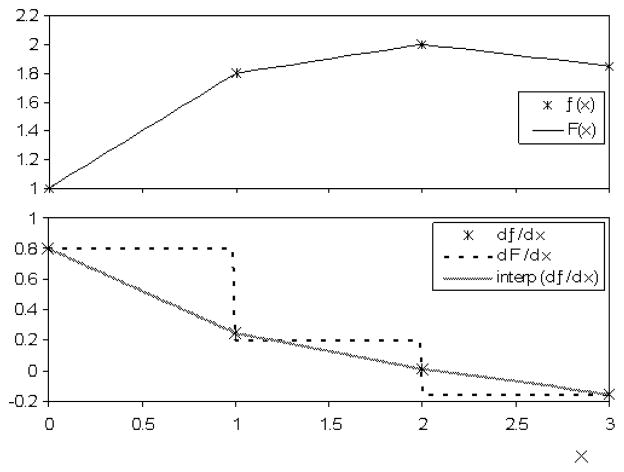
For linear interpolation, F(r⃗) = f(r⃗) at grid points, but the gradient of the interpolating function, ∇F, is not continuous nor is it equal to ∇f at the grid points (figure 2). A different method for determining gradients at intermediate grid locations is to apply linear interpolation to the ∇f values which results in a continuous function equal to ∇f at the grid points. For the latter method, however, the result is not equal to the gradient of the interpolating function F(r⃗). The consequences for either case, ∇F or interpolation of ∇f, are that iterative techniques will not be appropriate for linear interpolation (see section 2.4.2.iii). For non-iterative techniques, we use interpolation of ∇f because of its accuracy.

Figure 2.

Methods for determining derivatives of f(x) between grid points for linear interpolation. Top: An example of f(x) and the interpolation function F(x). Bottom: The derivative df/dx provided by central finite difference of f(x). which only exists at the grid points. Also shown are (a) dF/dx the derivative of the interpolation function F(x) and (b) the linear interpolation of df/dx. Method (b) is more accurate at the grid points with respect to the central finite difference.

Cubic spline interpolation fits a third-order polynomial to each point and has the advantages that ∇F = ∇f at grid points, ∇F is a continuous function, and it is a higher-order method and is therefore more accurate than linear interpolation. For a voxel that is a unit cube, extending from 0 to 1 in all dimensions (figure 3), the interpolating function has the form

Figure 3.

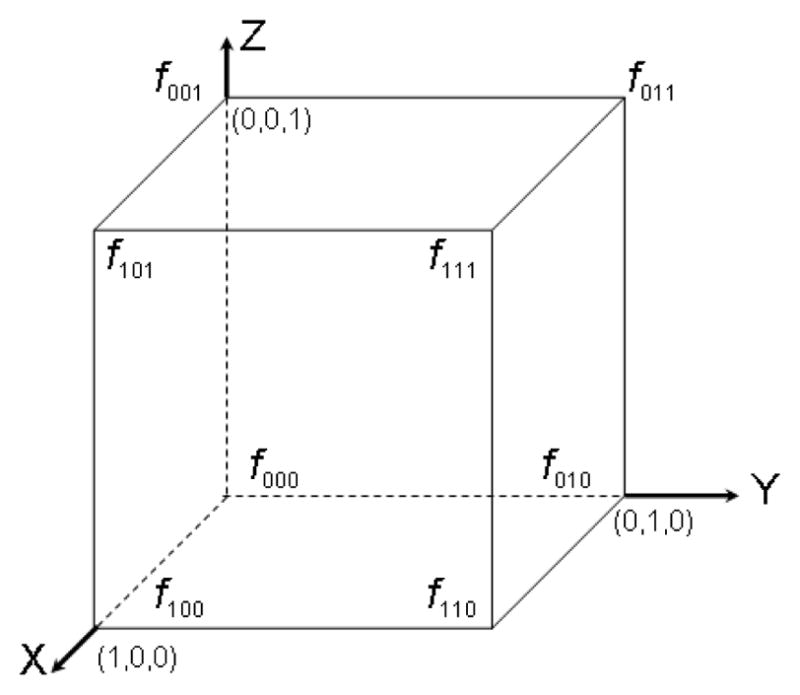
The function values, f_abc, at the corners of a unit cube that are used for interpolation at arbitrary (x, y, z) within the cube. There are 8 function values corresponding to the corners of the cube where, for example, f₀₀₁ represents the function value at (x, y, z) = (0, 0, 1).

$$F(x,y,z)=\sum _{i,j,k=0}^3{\alpha }_{\mathit{ijk}}{x}^i{y}^j{z}^k.$$ (9)

There are 64 polynomial coefficients and, therefore, 64 constraints are used to fit the polynomial. We use the tricubic spline interpolation method in Lekien and Marsden [9] given by

$$\overline{\alpha }=B^{-1}\overline{b}$$ (10)

where B⁻¹ is a 64 × 64 matrix of constants and ᾱ and b̄ are 64-element vectors given by

$$\overline{\alpha }=\left\{\begin{array}{l}{\alpha }_{000}\hfill \\ {\alpha }_{001}\hfill \\ {\alpha }_{002}\hfill \\ {\alpha }_{003}\hfill \\ {\alpha }_{010}\hfill \\ {\alpha }_{011}\hfill \\ {\alpha }_{012}\hfill \\ \dots \hfill \\ {\alpha }_{333}\hfill \end{array}\right\}\text{and}\overline{b}=\left\{\begin{array}{lll}{f}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}1-8\hfill \\ {\left(\frac{\partial f}{\partial x}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}9-16\hfill \\ {\left(\frac{\partial f}{\partial y}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}17-24\hfill \\ {\left(\frac{\partial f}{\partial z}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}25-32\hfill \\ {\left(\frac{{\partial }^{2}f}{\partial x\partial y}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}33-40\hfill \\ {\left(\frac{{\partial }^{2}f}{\partial x\partial z}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}41-48\hfill \\ {\left(\frac{{\partial }^{2}f}{\partial y\partial z}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}49-56\hfill \\ {\left(\frac{{\partial }^{3}f}{\partial x\partial y\partial z}\right)}_{\mathit{abc}}\hfill & ,\hfill & \text{elements}57-64\hfill \end{array}\right\}$$ (11)

Fortunately, many elements of the B⁻¹ matrix are zero and the computation time can be improved by writing the matrix equation as 64 separate equations, removing any terms with multiplication by zero, and factorizing the remaining terms. Furthermore. the ᾱ coefficients are calculated for all points only at the beginning of the problem and interpolation at various (x, y, z) uses the same coefficients by Eq. 9.

For 2-dimensional cubic interpolation, the same formalism is used except that any derivatives with respect to z are set to zero and any function value or derivative with c = l in the matrix equation are set to c = 0. This method allows re-use of the code in 2-dimensions. More information for both 2 and 3-dimensional cubic interpolation can be found in Ref [9].

Interpolated first-order derivatives are obtained by differentiating Eq. 9 and the ᾱ coefficients need not be re-calculated. For example,

$$\frac{\partial F}{\partial x}=\sum _{i=1}^3\sum _{j,k=0}^{3}i{\alpha }_{\mathit{ijk}}{x}^{i-1}{y}^j{z}^k.$$ (12)

While all first-order derivatives of F(x, y, z) are constrained at grid points by the tricubic interpolation method, not all of the second-order derivatives are constrained (see Eq. 11). The derivatives that are not constrained are not continuous nor equal to the second-order derivatives of f at the grid points. Interpolated second-order derivatives $\frac{{\partial }^{2}F}{\partial x^2},\frac{{\partial }^{2}F}{\partial x\partial y},\dots ,\frac{{\partial }^{2}F}{\partial z^2}$ are, therefore, obtained from linear interpolation of $\frac{{\partial }^{2}f}{\partial x^2},\frac{{\partial }^{2}f}{\partial x\partial y},\dots ,\frac{{\partial }^{2}f}{\partial z^2}$, respectively.

2.4. Taylor series

The minimum PSD problem expressed as a differential equation (Eq. 5) can be solved using r⃗ = 0 as the first guess of the solution point. The Taylor series of f(r⃗) and ∇f(r⃗) in the neighborhood of r⃗ = 0 are

$$f(\overrightarrow{r})\approx f(0)+(\overrightarrow{r}·\nabla )f(0)+\frac{1}{2}\overrightarrow{r}·[(\overrightarrow{r}·\nabla )\nabla f(0)]+O(\frac{{\partial }^{3}f(0)}{\partial r^3})$$ (13)

$$\nabla f(\overrightarrow{r})\approx \nabla f(0)+(\overrightarrow{r}·\nabla )\nabla f(0)+O(\frac{{\partial }^{3}f(0)}{\partial r^3})$$ (14)

Since |r⃗| ≲ 1 in the region of possible solutions with γ ≲ 1, we must again rely on the higher-order derivatives of f(r⃗) to be small to truncate this Taylor series. Those voxels where this approximation fails can be automatically detected by calculating the contribution of higher-order terms or by using iterative techniques and monitoring differences between successive iterations. For this subset of voxels, one can either use TAE, iteration and/or higher-order techniques to calculate γ.

2.4.1. Zeroth order solution

To zeroth order, f(r⃗) = f(0) and ∇f(r⃗) = 0. These approximations are inserted into Eq. 5 to yield x = y = z =0 as the point at minimum PSD. Using Eq. 6 and converting f(r⃗) back to dose, we have

$$\gamma ({\overrightarrow{\rho }}_0)=\left|\frac{D({\overrightarrow{\rho }}_0)-D_0({\overrightarrow{\rho }}_0)}{\delta D_0}\right|,$$ (15)

which is just the dose difference at ρ⃗ = ρ⃗₀.

2.4.2. First order solution

To first order, Eqs. 5, 13 and 14 become

$$\overrightarrow{r}=-[f(0)+\overrightarrow{r}·\nabla f(0)]\nabla f(0).$$ (16)

Since the factor in square brackets is just a scalar, the solution for r⃗ must lie along a line parallel to ∇ f(0) and passing through the origin. We call this the first-order search path. The use of a search path reduces the 3-dimensional PSD minimization problem to a 1-dimensional problem. We parameterize the displacement of a point along the search path by r⃗ = t∇f(0). After substituting this into Eq. 16 and canceling ∇f(0) from both sides of the equation, the solution for t is

$$t=-\frac{f(0)}{1+{[\nabla f(0)]}^2},$$ (17)

giving

$$\overrightarrow{r}=-\frac{f(0)\nabla f(0)}{1+{[\nabla f(0)]}^2}.$$ (18)

The spatial distance at minimum PSD is then simply |r⃗|, but we still need the dose difference function f(r⃗) at this position to calculate γ(ρ⃗₀) by Eq. 6. The dose difference, and hence γ-index, can be determined by:

1. Interpolation of f(r⃗) – Linear or cubic spline interpolation can be used to obtain f(r⃗) at the first-order solution for r⃗, which gives γ(ρ⃗₀) by Eq. 6.

2. Taylor expansion of f(r⃗) – To first order, f(r⃗) = f(0) + r⃗ · ∇ f(0) and the γ-index is

   $$\gamma ({\overrightarrow{\rho }}_0)=\frac{\mid f(0)\mid }{\sqrt{1+{\mid \nabla f(0)\mid }^2}}=\frac{\mid D({\overrightarrow{\rho }}_0)-D_0({\overrightarrow{\rho }}_0)\mid }{\sqrt{{(\delta D_0)}^2+{(\delta d_0)}^2{\left|\frac{\partial D(\overrightarrow{\rho })}{\partial \overrightarrow{\rho }}\right|}^2}}.$$ (19)

   This is the same result obtained by Bakai et al [1] and it can be calculated almost as fast as the 0th-order solution.

3. Iterations – Successive first-order approximations can be applied by interpolating f(r⃗) and ∇ f (r⃗) at the new solution point and solving equation 16 for an improved r⃗ solution. The r⃗ solution at the N^th iteration is given by

   $${\overrightarrow{r}}_N=-\frac{[f({\overrightarrow{r}}_{N-1})-{\overrightarrow{r}}_{N-1}·\nabla f({\overrightarrow{r}}_{N-1})]\nabla f({\overrightarrow{r}}_{N-1})}{1+{[\nabla f({\overrightarrow{r}}_{N-1})]}^2}.$$ (20)

This method can only be used if ∇f is a continuous function and equal to the gradient of the interpolating function for all r⃗ (see an example where this is not the case in figure 2). If it is not, then the iterations can fail to converge. For this reason, we only use cubic spline interpolation with the iteration method.

The dose distribution D(ρ⃗) within the δd₀ neighborhood of ρ⃗ is almost always a monotonic increasing or decreasing function and these iterations converge quickly. The situation whereby the iterations converge on a local minima of the PSD rather than the global minima can occur when D(ρ⃗) has discontinuities or has excessive noise. This scenario can be mitigated by selecting the smoothest dose distribution as D(ρ⃗) when deciding which distribution should be D(ρ⃗) and which should be D₀(ρ⃗₀) This choice is further discussed in section 4.7.

2.4.3. Second order solution

To second order, Eq. 5 becomes

$$\overrightarrow{r}=-\left[f(0)+\overrightarrow{r}·\nabla f(0)+\frac{1}{2}\overrightarrow{r}·[(\overrightarrow{r}·\nabla )\nabla f(0)]\right]\times [\nabla f(0)]+(\overrightarrow{r}·\nabla )\nabla f(0)+O(\frac{{\partial }^{3}f}{\partial r^3})]$$ (21)

Solving Eq. 21 for r⃗ is computationally expensive because it requires solving a set of coupled cubic equations. Similarly, the second-order search path

$$\overrightarrow{r}=t[\nabla f(0)+(\overrightarrow{r}·\nabla )\nabla f(0)]$$ (22)

can be solved for r⃗ (t), and while this is a linear problem that can be solved by matrix inversion, the result for a 3-dimensional problem has t³ terms that when substituted into equation 21 yields an intractable 7^th-order polynomial equation of a single variable (a 2-dimensional problem will be 5^th-order). There are multiple possible solutions to Eq. 21 because there are local and global minima and local maxima in the PSD from a point to a quadratic surface. Only the solution corresponding to the global minimum should be selected for the γ-index calculation.

We resort to a semi-second order method that is the solution to

$$\overrightarrow{r}=-\left[f(0)+\overrightarrow{r}·\nabla f(0)+\frac{1}{2}\overrightarrow{r}·[(\overrightarrow{r}·\nabla )\nabla f(0)]\right]{\overrightarrow{g}}_{\text{fo}}+O\left(\frac{{\partial }^{3}f}{\partial r^3},{\left[\frac{{\partial }^{2}f}{\partial r^2}\right]}^2\right),$$ (23)

where g⃗_fo ≡ ∇ f (0) + (r⃗_fo · ∇) ∇ f (0) and r⃗_fo is the first-order solution for r⃗. The term $\frac{1}{2}\overrightarrow{r}·[(\overrightarrow{r}·\nabla )\nabla f(0)]$ could also be simplified using r⃗ ≈ r⃗_fo while maintaining order ${\left[\frac{{\partial }^{2}f}{\partial r^2}\right]}^2$ but the solution for r⃗ is more accurate without making this approximation. Equation 23 can be solved with the substitution

$$\overrightarrow{r}=t{\overrightarrow{g}}_{\text{fo}},$$ (24)

and canceling g⃗_fo from both sides of the equation. The result is the quadratic equation

$$f(0)+t[1+({\overrightarrow{g}}_{\text{fo}}·\nabla )f(0)]+\frac{1}{2}{t}^2{\overrightarrow{g}}_{\text{fo}}·({\overrightarrow{g}}_{\text{fo}}·\nabla )\nabla f(0)=0$$ (25)

that is to be solved for t. Graphically, we are finding the intersection of a line with a parabola. When two solutions exist, one will be close to the 1^st-order solution point and the other will be at a different section of the parabola and we select the solution that reduces to the 1^st-order solution in the limit of small second-order derivatives. If no solution exists, then this corresponds to the graphical situation that the normal vector is not intersecting the parabola approximating f(r⃗) and we set t equal to the value at the mid-point of the parabola. Mathematically, this is given by

$$t=\{\begin{array}{l}(-b+\sqrt{b^2-4ac})/2a,b^2-4ac>0\hfill \\ -b/2a,\text{otherwise}\hfill \end{array}$$ (26)

where:

$$a=\frac{1}{2}{\overrightarrow{g}}_{\text{fo}}·({\overrightarrow{g}}_{\text{fo}}·\nabla )\nabla f(0),$$ (27)

$$b=1+({\overrightarrow{g}}_{\text{fo}}·\nabla )f(0),\text{and}$$ (28)

$$c=f(0).$$ (29)

The dose difference, and hence γ-index, can be determined by:

1. Interpolation of f(r⃗) – We use the higher-order cubic spline interpolation method to obtain f(r⃗) and hence obtain γ(ρ⃗₀).

2. Taylor expansion of f(r⃗) – Using equations 13, 24, and 27,

   $$f(\overrightarrow{r})\approx f(0)+t({\overrightarrow{g}}_{\text{fo}}·\nabla )f(0)+t^{2}a,$$ (30)
   and the γ-index follows from

   $$\gamma (\overrightarrow{r})=\sqrt{f{(\overrightarrow{r})}^2+{(t{\overrightarrow{g}}_{\text{fo}})}^2}$$ (31)

2.5. Computing platform

The software is developed in the Matlab R2007b technical computing environment without using compiled code (for optimum portability). The software is run on a Dell Precision Workstation T7400-64 bit with dual Quad Core Intel Xeon 2.66 GHz processors although calculation times are based on the use of a single core. All quoted computation times below are for this implementation.

2.6. Test Cases

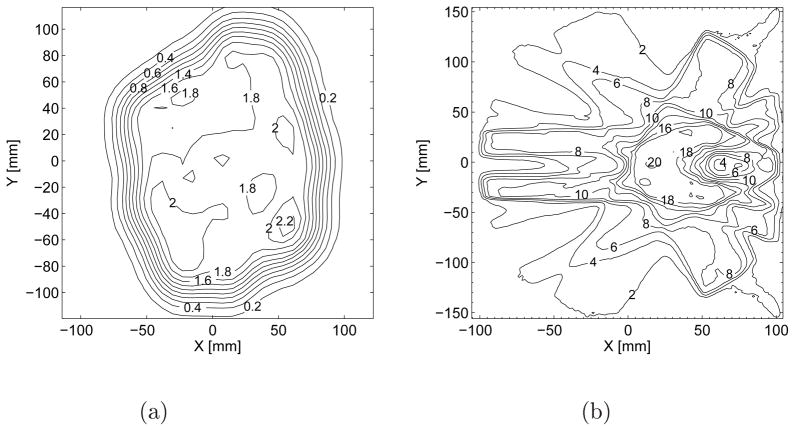
Results are generated for two test cases. The first (Fig. 4a) is a proton pencil beam scanning (PBS) treatment of osteosarcoma of the pelvis. The D(ρ⃗) dose distribution is a 3-dimensional dose grid from the Astroid treatment planning system [10] with 562 × 10³ voxels and 3×3×3 mm³ grid pitch. The D₀(ρ⃗₀) dose distribution comes from measurements at three depths with an I’mRT MatriXX detector^‡, a 2-dimensional array of 1024 ionization chambers with pitch 7.62 × 7.62 mm². The second test case (Fig. 4b) is an IMRT treatment of a spine tumor located around the spinal cord in a cylindrical phantom. The D(ρ⃗) dose distribution comes from the CMS treatment planning system^§ and the D₀(ρ⃗₀) dose distribution comes from an in-house developed Monte Carlo simulation [11]. Both IMRT dose distributions are specified on a 3-dimensional grid with 1.78 × 10⁶ voxels and 2 × 2 × 2.5 mm³ grid pitch.

Figure 4.

(a) Measured proton PBS dose distribution at 162 mm depth of polystyrene for the treatment of osteosarcoma of the pelvis and (b) Simulated photon IMRT dose distributions at the plane containing the isocenter for the treatment of a spine tumor located around the spinal cord. The simulated photon distribution is corrected for an 18% normalization factor and then shifted in X by 0.1 mm for the purposes of this work to force the γ-index software to perform interpolation. The units of the contours in (a) and (b) are [GyRBE] and [Gy], respectively.

3. Results

The preceding section describes a variety of methods for calculating γ(ρ⃗₀), a matrix of γ values specified on the same grid as the D₀(ρ⃗₀) dose distribution. Tab. 1 enumerates the methods with labels A through I.

Table 1.

Enumeration of γ-index calculation methods from Sections 1 and 2.

Label	Method Type	Interp. method for Taylor series	Calculation of f(r⃗) at PSD	Reference
A	TAE	-	Tricubic	Low 1998 [2]
B	TAE	-	Linear	Low 1998 [2]
C	0th order	-	Linear	Section 2.4.1
D	1st order	Tricubic	Tricubic	Section 2.4.2.i
E	1st order	Linear	Taylor series	Bakai 2003 [1]
F	1st order	Tricubic	Taylor series	Bakai 2003 [1]
G	1st order	Tricubic and Iterations		Section 2.4.2.iii
H	2nd order	Tricubic	Tricubic	Section 2.4.3.i
I	2nd order	Tricubic	Taylor series	Section 2.4.3.ii

We define P_γ≤1 as the fraction of γ values less than or equal to 1 within a region of interest, the quantitative pass/fail criteria for comparing two dose distributions. Usually P_γ≤1 >90% is required to pass.

Calculation times for TAE methods, Methods A and B, are based on a brute-force approach whereby P_γ≤1 is determined using an interpolated grid of pitch δd₀. P_γ≤1 is re-calculated on a grid with half the pitch for points with γ > 1 and repeated until P_γ≤1 converges within 0.1%. These calculation times are not optimized and the purpose is to give the value of the γ-index for these methods. The calculation times could be improved through techniques such as those described in Wendling et al 2007 [5], but the calculation time for any search-type method is sensitive to the interpolation method, agreement between the two dose distributions, and the pitch of the grid used in the search.

The calculation time for each numerical method includes interpolation and the calculation of the ᾱ coefficients, which is generally the largest contribution to the total calculation time. All numerical methods except Method G (1^st-order Tricubic Spline and Iterations) calculate the matrix of γ-index values on the entire ρ⃗₀ grid, regardless of the region of interest. Method G performs an initial 1^st-order calculation on the entire ρ⃗₀ grid and then 1^st-order iterations on points only within the region of interest that have not converged within 0.2% relative to the most recently iterated γ(ρ⃗₀). Iterations stop when more than 99% of points converge. The computation time of methods C through I could be improved by computing only within the region of interest. At our facility, however, we wish to qualitatively examine all regions of the γ-index map in addition to the value of P_γ≤1 as part of the quality assurance program, so the γ-index software has been developed for that purpose.

Throughout this section, we use ρ⃗ = (X, Y, Z), with upper-case X, Y, and Z and units of [mm] to denote physical coordinates. Unit-less spatial coordinates defined by Eq. 2 are in lower-case letters.

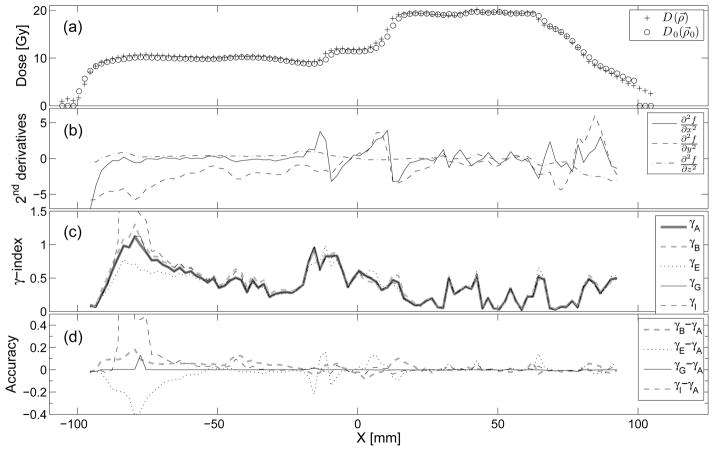
For the first test case, the 3-dimensional and 2-dimensional γ-index comparisons are given in Tabs. 2 and 3, respectively. For the second test case, the 3-dimensional γ-index comparison is given in Tab. 4. In the second test case, a line of grid points parallel to the X direction at Y = −31.8 mm and Z = 10 mm has particularly large second-order derivatives and results at these points are given in Fig. 5.

Table 4.

Results for the 3-dimensional γ-index for the IMRT test case in Fig. 4b. The comparison uses δd₀ = 3 mm, δD₀ = 3%, and region of interest denned by 30% of the maximum dose. IMRT uses collimators to shape the dose distribution which tests the limits of the numerical techniques. In this case, even in the presence of collimators, both the 1^st-order Method F and 2^nd-order Method I give P_γ≤1 with ~ 1% accuracy.

	Pγ≤1 [%]	Accuracy [%]	Calculation time [s]
A	90.80	-	22000
B	89.88	1.0	2300
C	37.97	58	1.5
D	81.65	10.1	36.7
E	91.80	1.1	4.7
F	91.75	1.1	28.0
G	90.71	0.1	34.7
H	88.71	2.3	51.9
I	90.04	0.8	35.6

Figure 5.

(a) IMRT dose distributions along the X direction at Y = −31.8 mm and Z = 10 mm. (b) Second derivatives of the dose difference function defined by Eq. 3 with respect to the unit-less spatial coordinates, (c) γ (ρ⃗₀) by methods defined in tab. 1. (d) Accuracy of the γ-index methods with respect to γ_A · γ_B shows the magnitude of the error in individual voxels (~ ± 0.1) caused by linear interpolation alone. γ_E and γ_I are more accurate than γ_B except in regions where the 2^nd derivatives and γ are large. γ_G is the most accurate of the four methods compared to γ_A.

4. Discussion

4.1. First-order method with f(r⃗) from the Taylor expansion

Equation 19 was first constructed by Bakai et al [1] and they proposed a new comparison index that has both positive and negative values, given by

$$\chi ({\overrightarrow{\rho }}_0)\equiv \frac{D({\overrightarrow{\rho }}_0)-D_0({\overrightarrow{\rho }}_0)}{\sqrt{{(\delta D_0)}^2+{(\delta d_0)}^2{\left|\frac{\partial D(0)}{\partial \overrightarrow{\rho }}\right|}^2}}.$$ (32)

The χ-index has similar behavior to the γ-index; in regions where D(ρ⃗₀) is flat, χ is equal to the dose difference and in regions where the dose distribution is not flat, |χ| is reduced because the gradient of the dose distribution is in the denominator.

For the IMRT and proton PBS examples in Sec.3, we find that |χ| ≃ γ except where second derivatives and γ are large. Regions that have small second derivatives or have small γ (and hence small r) allow us to accurately truncate the Taylor series after the 1^st-order terms in Eqs. 13 and 14. The results for “γ_E − γ,_A” in Fig. 5d show that |χ| is generally accurate within ±0.2 in individual voxels, although the accuracy can be between ±0.2 to 0.4 in the aforementioned regions. The accuracy of summing the number of voxels with γ ≤ 1 is much better than the accuracy of individual voxels because the uncertainties in this method are centered around zero. We, therefore, arrive at a similar result to Bakai in our examples, that the method gives P_γ≤1 with ~ 1% accuracy.

4.2. Signed γ-index

The χ evaluation factor, which can be positive and negative depending on the sign of D (ρ⃗₀) − D₀(ρ⃗₀), is useful because it indicates the locations where the dose distribution D(ρ⃗₀) is smaller or larger than D₀(ρ⃗₀). This makes it very simple to diagnose discrepancies due to spatial shifts and/or output from a display of the χ-index matrix. One can always construct a signed γ-index with the same usefulness from any of the methods in Sec. 2 by multiplying γ(ρ⃗₀) by the sign of D(ρ⃗₀) − D₀(ρ⃗₀).

4.3. γ-index of field combinations

Both IMRT and proton PBS use field combinations such that the cumulative dose is largely uniform in the target region while the individual fields can be non-uniform. The individual fields can have steeper dose gradients on average than the sum of the fields which reduces the γ-index in individual voxels because the gradient of the dose is in the denominator in Eq. 19. It is, therefore, generally more conservative to use the sum of the field combinations in a γ-index comparison than the individual fields.

4.4. Two-dimensional dose distributions

The γ-index methods have been developed in this work for 3-dimensions. The 2-dimensional γ-index is appropriate, however, whenever the dose distribution is predominantly independent of the longitudinal coordinate. In these 2-dimensional beams, the differential equation in Eq. 5 gives the trivial solution z =0 whenever $\frac{\partial f}{\partial z}=0$ and one can, therefore, apply either a 2 or 3-dimensional γ-index method and achieve mathematically equal results.

4.5. Local dose and distance tolerances

While the distance and dose tolerances in Eqs. 2 and 3 are constant, one may use numerical methods with a non-isotropic distance tolerance and spatially varying dose tolerance. The methods in section 2.1 are unchanged with this modification but it must be kept in mind that eq. 5 is derived for a single voxel at a fixed ρ₀ grid point. Only the D(ρ⃗) dose distribution is varying in the derivative of f(r⃗), with D₀(ρ⃗₀) and δD₀(ρ⃗₀) held constant at the local value. For example, for a spatially varying dose tolerance, the central finite difference in eq. 7 becomes

$$\frac{\partial f(\overrightarrow{r})}{\partial x}=\delta d_0\left[\frac{D({\rho }_1+\mathrm{\Delta }{\rho }_1)-D({\rho }_1-\mathrm{\Delta }{\rho }_1)}{2\mathrm{\Delta }{\rho }_1}\right]\frac{1}{\delta D_0(\overrightarrow{\rho }0)}.$$ (33)

4.6. Comparison of numerical methods

The 1^st-order iterative method with tricubic spline (Method G) is fast and accurate in all of the examples and the iterations can be used to check for convergence. The calculation time for the 3-dimensional γ-index is 34.7 s for 1.78×10⁶ voxels for the IMRT case and the accuracy of P_γ≤1 is better than 0.2% in our examples.

Significant time-savings can be made if the second derivatives of f(r⃗) are known to be small. Method E (originally derived in Ref. [1]) is faster than Method G by about a factor of 10 and the accuracy of P_γ≤1 with this method is ~1% in our examples.

The methods that use Taylor series to obtain f(r⃗) at the solution point (Methods E, F and I) are faster than those of the same order that use interpolation (Methods D and H). The advantage of the latter is that f(r⃗) corresponds to a real point on the D(ρ⃗) dose surface and can be considered to always underestimate the true γ-index with magnitude depending on how well the numerical methods find the solution to Eq. 5. The uncertainty in the former method on γ(ρ⃗₀) is positive or negative in individual voxels (depending on how well the Taylor series approximates the tricubic or linear interpolation) and will mostly average to zero when summing voxels to calculate P_γ≤1. Tab. 4 shows these effects: Method D underestimates P_γ≤1 by 10.1% compared to Method A (the “gold standard”); Method H, which is a 2^nd-order method, finds a better solution point, but still underestimates P_γ≤1 by 2.3%; and, Methods E, F and I, which use the Taylor series to obtain f(r⃗), are all accurate within 1.1% with Method I, the 2^nd-order method, being the most accurate.

By combining the 1^st and 2^nd-order methods, one can automatically determine the accuracy of γ(ρ⃗₀) voxel-by-voxel and perform iterations or TAE methods in selected voxels. The advantage of this approach over an iteration-only approach will depend on the dose distributions and the software implementation. In our implementation, the possible saving in the calculation time is at most a factor of 1.6 for the proton PBS example and no saving at all for the IMRT example compared to Method G.

4.7. Choice of evaluation and reference dose distributions

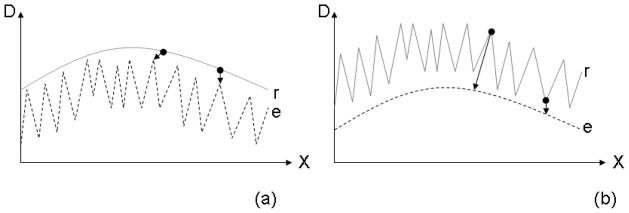
The γ-index compares two dose distributions which are called the evaluation and reference dose distributions. The evaluation distribution, D(ρ⃗), is searched for the smallest PSD to each point in the reference distribution, D₀(ρ⃗₀). As pointed out in Low 2010 [12] the gamma index result is not the same if the evaluation and reference distributions are interchanged. This is a result of the definition of γ in Eq. 1 where the minimization is performed over only one dose distribution coordinate and the user must decide over which coordinates to perform the search. Furthermore, another asymmetry occurs in the presence of noise artifacts. Noise introduced to the evaluation distributions (Fig. 6a) is very different compared to noise introduced to the reference distribution (Fig. 6b). Noise in the evaluation distribution artificially improves the γ-index while noise in the reference distribution merely “smeares” the matrix of γ values (i.e. some grid points will have smaller γ but they are compensated by points with larger γ). A small amount of noise in the latter distribution will, therefore, not cause a systematic error in P_γ≤1. Larger noise levels can affect the equilibrium between grid points that transition from γ > 1 to γ < 1 and vice versa depending on the number of initial grid points in each case, so a level of noise that is acceptable in the reference distribution depends on the flatness of the histogram of γ values near γ = 1. Noise artifacts are also discussed in Low 2010 [12].

Figure 6.

An extreme example of the asymmetry in the gamma index calculation. (a) The evaluated dose distribution “e” has almost 100% noise and (b) the reference dose distribution “r” has almost 100% noise. The smallest PSD between the two curves, assuming the δd₀ and δD₀ gamma index parameters are unity, are indicated by the length of the arrows at two different points on the curves.

We use the dose distribution from treatment planning (or the smoother of the two distributions) as the evaluation distribution, D(ρ⃗) for the following reasons:

1. it does not have noise so this choice generally will not give false positive results;

2. it is continuous (except in regions directly behind collimators), a requirement for the numerical techniques;

3. it is calculated in 3-dimensions so the search for minimum PSD can be performed in 3-dimensions even when the reference dose is measured in only 1 or 2-dimensions. Performing measurements on a 3-dimensional grid to obtain a measured evaluation distribution would be cumbersome.

4. it is typically smooth and specified on a grid with pitch ≳ 2 mm which is approximately equal to the distance tolerance in the γ index. In this case, it is unlikely to have local minima in the search for minimum PSD (see Sec. 4.8).

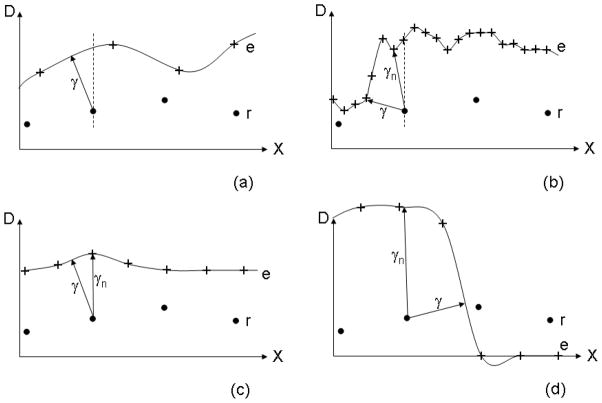
4.8. Local minima

The formation of local minima in the search for minimum PSD can distort the calculation of the γ-index. Fig. 7 gives schematics of a nominal case and three cases where the numerical methods can fail to find the global minimum. These limitations. however, are not unique to the numerical methods. TAE methods that stop the search as soon as the PSD increases with spatial distance (for example Ref. [5]) can also be distorted by local minima.

Figure 7.

(a) A nominal example of the reference dose grid (circles), evaluated dose grid (crosses), and cubic interpolation of the evaluated dose (solid line). In this case, numerical methods will determine γ correctly, represented by the length of the arrow, (b) An example where the numerical methods could be distorted by a local minimum (γ_n) instead of the true γ. (c) A maximum in the evaluated dose that exactly coincides with a reference dose grid position will fail to give the true γ at that grid point, (d) Discontinuities can lead to a failure due to negative dose from the cubic interpolation and local minima.

Generally, the case in Fig. 7c is statistically improbable and has no effect clinically and the cases outlined in Figs. 7b and d can be avoided if the evaluation distribution is smooth and specified on a grid of pitch approximately the same size as the distance tolerance, δd₀. In our experience, the dose distribution from treatment planning systems often has these properties. This scenario, where δd₀ is similar to the grid pitch, does not normally have local minima in the search for minimum PSD because the grid resolution is not small enough to create a local minimum (Fig. 7a). We stress, however, that numerical techniques might locate local minima in a few points where the second order or higher gradients are very large with the number of points affected comparable to other γ-index techniques that have truncated search algorithms.

5. Conclusions

We present an efficient method for calculating the 3-dimensional γ-index with tricubic spline interpolation. A numerical framework was created to solve for the minimum PSD to arbitrary order and we presented 0^th, 1^st, and semi 2^nd-order solutions. Examples of dose distributions from IMRT and proton PBS were used to test the numerical methods which assume that the evaluated dose distribution is continuous. The IMRT case shows the performance of these calculations in an extreme example where the dose distribution is shaped by multi-leaf collimators.

P_γ≤1 determined using linear interpolation and tricubic spline interpolation are different by ~1%. P_γ≤1 using 1^st-order numerical methods are also accurate within ~1% and are the best choice if the dose distribution is known to have small second-order derivatives. The semi 2^nd-order method is also accurate within ~1% and the difference between the 1^st and 2^nd-order methods can be used to check for convergence. Voxels that do not converge can be selected automatically and the calculation refined using iteration or TAE techniques.

P_γ≤1 in the 1^st-order iteration method is accurate within 0.2% and, in the IMRT example, the 3-dimensional γ-index calculation in 1.78 × 10⁶ voxels including tricubic spline interpolation is performed in 34.7 s. The convergence of the calculations can be checked automatically between iterations and, in our experience, this method is the best choice of the numerical methods if the dose distributions may have large second-order derivatives.

Table 2.

Results for the 3-dimensional γ-index for the PBS test case in Fig. 4a. The comparison uses δd₀ = 3 mm, δD₀ = 3%, and region of interest denned by 20% of the maximum dose. The depths d₁, d₂, and d₃ are 54 mm, 108 mm, and 162 mm of polystyrene, respectively. At each depth, 1024 measured points in a plane are compared to 562 × 10³ voxels from treatment planning. Method A is used as the “gold standard” for determining the accuracy of the other methods. The accuracy of Method B shows that linear interpolation introduces ~ 1% error. Method E is the fastest method with ~ 1% accuracy. Method I is slower than than Method E by a factor of 10, but it can be used to check the magnitude of 2^nd-order terms. Method G is only slightly slower than the 2^nd-order methods and has accuracy better than 0.2%.

	Pγ≤1 [%]	Depth d1 Accuracy [%]	Calc. time [s]	Pγ≤1 [%]	Depth d2 Accuracy [%]	Calc. time [s]	Pγ≤1 [%]	Depth d3 Accuracy [%]	Calc. time [s]
A	94.38	-	88.2	99.46	-	2.3	96.46	-	8.1
B	93.25	1.2	1.3	99.46	0.0	1.2	95.63	0.9	5.3
C	52.72	44	0.0016	68.93	31	0.0015	62.82	35	0.0017
D	93.45	1.0	0.14	98.39	1.1	0.14	96.26	0.2	0.14
E	93.25	1.2	0.018	99.29	0.2	0.019	96.46	0.0	0.018
F	92.88	1.6	0.13	99.11	0.4	0.14	98.03	1.6	0.13
G	94.38	0.0	0.28	99.28	0.2	0.29	96.46	0.0	0.28
H	94.01	0.4	0.17	99.28	0.2	0.17	96.46	0.0	0.17
I	93.26	1.2	0.16	99.46	0.0	0.17	96.46	0.0	0.16

Table 3.

Results for the same conditions as Tab. 2 except that the comparison uses a 2-dimensional γ-index. Depth d₃ is chosen for the comparison. These data show that the algorithms developed in 3-dimensions can be applied in 2-dimensions.

	Pγ≤1 [%]	Accuracy [%]	Calculation time [s]
A	95.86	-	0.18
B	95.46	0.4	0.11
C	63.31	34	0.0014
D	95.71	0.15	0.043
E	96.25	0.4	0.0039
F	96.30	0.5	0.033
G	95.91	0.05	0.048
H	95.91	0.05	0.049
I	95.91	0.05	0.057