Abstract
Purpose: The purpose of this work was to investigate the relationship between dynamically accumulated dose (dynamic dose) and 4D accumulated dose (4D dose) for irradiation of moving tumors, and to quantify the dose uncertainty induced by tumor motion.
Methods: The authors established that regardless of treatment modality and delivery properties, the dynamic dose will converge to the 4D dose, instead of the 3D static dose, after multiple deliveries. The bounds of dynamic dose, or the maximum estimation error using 4D or static dose, were established for the 4D and static doses, respectively. Numerical simulations were performed (1) to prove the principle that for each phase, after multiple deliveries, the average number of deliveries for any given time converges to the total number of fractions (K) over the number of phases (N); (2) to investigate the dose difference between the 4D and dynamic doses as a function of the number of deliveries for deliveries of a “pulsed beam”; and (3) to investigate the dose difference between 4D dose and dynamic doses as a function of delivery time for deliveries of a “continuous beam.” A Poisson model was developed to estimate the mean dose error as a function of number of deliveries or delivered time for both pulsed beam and continuous beam.
Results: The numerical simulations confirmed that the number of deliveries for each phase converges to K/N, assuming a random starting phase. Simulations for the pulsed beam and continuous beam also suggested that the dose error is a strong function of the number of deliveries and/or total deliver time and could be a function of the breathing cycle, depending on the mode of delivery. The Poisson model agrees well with the simulation.
Conclusions: Dynamically accumulated dose will converge to the 4D accumulated dose after multiple deliveries, regardless of treatment modality. Bounds of the dynamic dose could be determined using quantities derived from 4D doses, and the mean dose difference between the dynamic dose and 4D dose as a function of number of deliveries and/or total deliver time was also established.
Keywords: 4D CT, 4D planning, interplay effect
INTRODUCTION
The interplay between the incident beam and tumor motion could potentially introduce dosimetric error that cannot be compensated for by increasing target margin,1, 2, 3, 4, 5 for IMRT, VMAT and scanning beam proton, or heavy-ion radiotherapy. In an ideal situation, to account for the interplay effect, the dose should be calculated with the real-time beam fluence rate and patient volume image and accumulated over time, termed the dynamically accumulated dose (dynamic dose).6 However, since patient breathing pattern, patient anatomy, and the beam properties could all vary during the patient treatment, it is not possible to obtain the dynamic dose at the time of treatment planning, and the planned dose that does not account for the interplay effect could deviate from the dynamic dose. Quantitative studies and measurements have shown a 2%–3% systematic difference between the delivered dose and the 3D dose generated on a static CT (3D static dose, or static dose),3, 7, 8 up to more than 5% difference for VMAT,3 and over 10% for scanning beam proton9 radiotherapy, even with fractionated delivery. A previous study by Bortfeld et al.10 concluded that for IMRT with tumor motion, the expected dose value is a weighted average of the dose distribution without motion. However, this work assumed that the spatial dose distribution does not change with organ movements, which may not be a good assumption for IMRT in inhomogeneous tissue,11 and does not hold for proton therapy. In addition, they also assumed that the distribution of a particular voxel has a probability density function of , which is only a function of location. This assumption could lead to the possibility of systematic error, as shown by Evans et al.12 Furthermore, since in practice there is no practical way to determine for an individual patient, the “weighted average of the dose distribution without motion” is often further approximated by the dose distribution without motion or the 3D static dose.13 With the availability of 4D respiration-correlated computer tomography (CT) and deformable registration, 4D accumulated dose (4D dose) distribution calculation can be performed with the tumor motion being correlated with time () or phase (). Studies have shown that the 4D dose can differ significantly from the 3D static dose, calculated on any single-phase or average CT, for both photon14, 15 and scanning beam proton16, 17 radiotherapy. It has also been shown that 4D planning and optimization for IMRT could indeed improve tumor coverage and/or reduce the dose to normal tissue, compared with single-phase planning and optimization.14, 18, 19 However, the relationship between the 4D dose and the dynamic dose was not fully investigated, and to date there were no established technique to quantify the patient specific motion induced dose uncertainty at the time of treatment planning.
The purpose of this work was to determine the relationship between the dynamic dose and the 4D dose, and develop a technique to predict the maximum and mean dose error induced by tumor motion for individual patients without repeated dose calculation. Throughout this work, we assume there was no residual motion within a 4DCT phase.
METHODS
Dynamic dose and 4D dose
Let Ep(t) denote the planned fluence rate of an incident (photon or proton) beam at a given instant t and let denote the static 3D patient volume image. The static dose to the patient is a (complex) function of E and V and can be written as
| (1) |
where is the total fluence of the beam and Td is the time required to deliver the total fluence.
If the same planned Ep(t) is delivered to a moving tumor, and if we can somehow acquire the fluence and patient volume data at any given time (), the dynamically accumulate dose to the patient can then be written as
| (2) |
where E(t) = Ep(t − Δt) represents the timing difference between the actual delivery and the plan. In ideal case E(t) = Ep(t − t0) where t0 represents instant when the deliver starts. Note that dynamic dose to patient can be calculated if and only if we know the fluence rate, the patient volume, as well as the registration vectors, at any given t, which may not be possible. The 4D accumulated dose, on the other hand, was calculated based on the motion information collected at the time of the simulation, and could be written as
| (3) |
where n is a phase of breathing cycle, is the patient volume at phase n, and N is the total number of phases. As indicated by the equation, the planned fluence was applied to each of the N phases, and the 4D dose was the averaged sum of doses to individual phases.
Suppose the treatment plan was repeatedly delivered for K times, by means of such as repainting, fractionated delivery, etc., the dynamic dose over these deliveries, assuming perfect deliveries where fluence rate at any given time t after the treatment started are identical for all delivers (Ek(t + t0(k)) = Ep(t)), could then be written as
| (4) |
For any given time instant t, the phase the patient is in (n(t)) can be determined by , or , where Tb is the patient breathing cycle and r ∈ N is an arbitrary integer. If each delivery were binned according to different phases, assuming that all phases have the same time length, with no residual motion within a phase, and that the patient's breathing is a perfect periodic function, then the total time the patient is in for each phase n during deliver k can be written as
| (5) |
and Eq. 4 can be rewritten as
| (6) |
For each and any fixed t ∈ [0, Td] and n ∈ {1…N}, assuming t0(k) are independent variables uniformly distributed over [0,Tb), then the probability . Therefore when K → ∞ for each t ∈ [0, Td] there would be K / N instances of t falls in phase n, or
| (7) |
Thus we showed that under ideal conditions, namely all deliveries were identical to the plan except the starting time, which were uniformly distributed over N phases, all phases had the same time length, with no residual motion within a phase, and that the patient's breathing being a perfect periodic function, after multiple deliveries, the dynamic dose converges to the 4D dose and not the 3D static dose. As mentioned in Sec. 1, discussion of the difference between the 4D dose [Eq. 3] and the 3D static dose [Eq. 1] can be found in several papers.14, 15, 16, 17, 18
If the repeated deliveries were not identical, instead of delivering the planned Ep(t) at time t + t0(k), it was actually delivered at time, for example, t + t0(k) + tk, i.e., Ek(t + t0(k) + tk) = Ep(t) where tk ∼ N(0,σ) is a Gaussian distributed random variable, now
| (8) |
and it is still easy to show that Eq. 7 holds. In addition to modeling the delivery timing of the beam fluence, Eq. 8 also partially modeled the irregular breathing pattern of the patient (starting phase n at time t + tk instead of t), with the assumption that the breathing magnitude did not change, and indicated that even with an irregular breathing pattern, the relationship in Eq. 7 still holds.
Quantification of interplay effect
The interplay effect can be quantified as the dose difference between the dynamic dose and the 4D or 3D static dose. In other words, 4D dose is an unbiased estimator of the dynamic dose as shown in Sec. 2A, and interplay effect is the estimation error using the 4D or 3D static dose to estimate the dynamic dose, without knowledge of the patient during treatment. For a single delivery, the maximum dose with, or the upper bound of, the dynamic dose for any given voxel can be calculated as
| (9) |
To calculate Dmax in step and shoot IMRT, for each voxel, the dose on all N phases for each segment was calculated, and Dmax was the summation of the maximum dose among the phases for each segment. To calculate Dmax in spot scanning proton RT, for each voxel, the dose on all N phases for each spot was calculated, and Dmax was the summation of the maximum dose among the phases for each spot. To enable dose summation, deformable registration was implied. The dose difference between Dmax and the 4D dose D′, which also is the upper bound of positive dose error (overshoot) using 4D dose instead of dynamic dose, after any possible single delivery, is
| (10) |
Likewise, Dmin and ΔDmin can also be established. It can be observed that ΔDmax is different from comparing the accumulated dose calculated on single phases with D′, since the maximum (or minimum) dose could be made up by dose delivered to different phases. Also note that ΔDmax is not a function of t0, and can be calculated during the 4D dose calculation.
Because Dmax and Dmin are simply the upper and lower bounds of the dose for a given fluence during a dynamic delivery, the maximum dose error using the 3D static dose to approximate the dynamic dose could also be calculated, similar to Eq. 10:
| (11) |
The relationship between ΔD and the number of deliveries will be investigated using simulation.
Simulations
We performed simple numerical simulations without patient dose calculation to show the convergence of the number of deliveries each phase received for a random time spot during delivery, and to show the decreasing trend of dose difference between the 4D and dynamic doses with increasing treatment time. The relationship between dose error, breathing cycle, and the delivery time will also be investigated. Comprehensive dosimetric studies have been performed and reported for both scanning beam proton9, 20, 21 and photon3, 7 radiotherapy and will not be repeated in this study, but the results from these studies will be summarized and discussed in Sec. 4.
Number of deliveries for each phase
The first set of simulations was designed to show that for any given time t during the delivery, after K deliveries, there would be K/N deliveries of Ep(t) at phase n. For this simulation, Tb = 6 s, Td = 300 s, and K = 500 deliveries were used. For the total number of phases, N = 3 was used without losing generality for a better demonstration. The simulations performed were as follows:
Perfect repeated deliveries with fixed t0 over all deliveries. All deliveries were identical, and with the same starting phase, a t ∈ [0, Td] was randomly selected and fixed over all deliveries, where Ep(t) represents a certain fluence planned to be delivered; for each delivery Ep(t) was delivered to a phase (n) at time t + t0 (Ek(t + t0) = Ep(t)), and the number of deliveries for each phase was tallied.
Perfect repeated deliveries with random t0. All deliveries were identical, and the starting phase for each delivery was an independent uniformly distributed random variable t0(k) ∼ U[0, Tb). A t ∈ [0, Td] was randomly selected and fixed over all deliveries; for each delivery Ep(t) was delivered to a phase (n) at time t + t0, and the number of deliveries for each phase was tallied.
Nonperfect repeated deliveries with random t0. Each delivery was randomly deviate from the perfect delivery, i.e., Ek(t + t0(k) + tk) = Ep(t), where tk ∼ N(0, σ), σ was arbitrarily chosen to be 3 s, and t0(k) ∼ U[0, Tb). A t ∈ [0, Td] was randomly selected and fixed over all deliveries; for each delivery Ep(t) was delivered to a phase (n) at time t + t0(k) + tk, and the number of deliveries of Ep(t) for each phase was tallied.
Pulsed beam simulations
The second set of simulations was designed to investigate a “pulsed beam,” where a given dose was delivered by pulses of repeating beams. Suppose a fluence map was designed to deliver a certain fluence F0, by adjusting the fluence rate E; this fluence could be delivered using K pulses, where
| (12) |
| (13) |
tk is the time when the kth pulse occurs, assuming each pulse was delivered instantaneously (Td → 0). An example of the scenario is a spot in the scanning proton beam, giving the same total MU with a different number of repaints.13, 22
We use the 4D dose to estimate the dynamic dose:
| (14) |
With Eq. 10, the maximum estimation error is
| (15) |
Next we investigated the mean estimation error using the 4D dose to estimate the dynamic dose as a function of number of pulses. For this set of simulation, Tb = 6 s, N = 10, t0 ∼ U[0, Tb), and K = 1–300 deliveries were used. The simulations performed were as follows: For each delivery, the fluence E = F0/K was delivered at time tk to a phase n. We assumed the delivery was a Poisson process, and the interdelivery time Δtk = tk−tk−1 was modeled as an exponential distribution with mean of 1/λ. We simulated the interval between deliveries using different 1/λ between 0 and 0.3 s, with increments of 0.01 s, where for 1/λ = 0 the deliveries were repeated K times at t0. These parameters resulted in a mean total delivery time of 0–90 s. The number of pulses that was delivered to each phase n (v(n)) was tallied, and the deviation from the 4D value v′(n) = K/N [Eq. 14] was calculated as . For simplicity, here we assume that all phase deviations from the 4D value would lead to the maximum dose error. For example, if all K pulses were delivered to a single phase, the dose error would be ΔDmax, regardless of which phase the pulses actually delivered to, and the deviation from the 4D value in this case is
| (16) |
The dose difference between the 4D dose and the dynamic dose (ΔD) then can be written as a ratio to ΔDmax as
| (17) |
The simulation was repeated 5000 times, and the mean dose difference between the 4D dose and the dynamic dose as a function of K was evaluated.
From the discussion in Sec. 2B, we can safely model the number of deliveries to each phase n as a Poisson process with mean ν = K/N. Note that the mean absolute deviation (MAD) is defined as
| (18) |
and comparing Eq. 17 with Eq. 18, Eq. 17 can be rewritten as
| (19) |
where MADpoisson(v) is the MAD of a Poisson process with mean v and can be calculated with23
| (20) |
The simulation results were compared with the calculation with the Poisson model in Eq. 19.
We also investigated a special case of the pulsed beam, where instead of modeling the interdelivery time Δtk as an exponential distribution, a fixed interval of Δt = 0.1 s was used with all other parameters remaining the same. In this case, each phase get the same number of deliveries every breathing cycle (Tb, or Tb /Δt deliveries), i.e., the 4D dose perfectly predict the dynamic dose, regardless of the starting phase (ΔD = 0). Therefore the number of deliveries to each phase still has a mean of K/N but is no longer a Poisson distribution. However, we can still model the number of deliveries within a breathing cycle as Poisson. Since the duration of each phase is Tb / N, and during that time consecutive pulses were delivered to the same phase, these pulses could be combined and viewed as one effective pulse, with magnitude of . The expected total effective number of combined pulses each phase received after K deliveries therefore can be written as
| (21) |
or effectively, each phase got exactly one combined pulse every breathing cycle (Tb). The expected effective number of combined pulses received for each phase within the last breathing cycle is the deviation from a full breathing cycle:
| (22) |
which can be modeled as a Poisson process for each phase. Using the effective number of combined pulse in Eqs. 21, 22, the Poisson estimation of the dose error can then be written as
| (23) |
Results of Eq. 23 were compared with the simulated mean dose difference between the 4D dose and the dynamic dose.
Continuous beam simulations
The third set of simulations was designed to investigate a “continuous beam,” where a continuous fluence was delivered over a certain amount of time (Td). Again, suppose a fluence map was designed to deliver a certain fluence F0, by adjusting the fluence rate E, which remains constant throughout the delivery; this fluence could be delivered in an amount of time Td, where
| (24) |
| (25) |
Examples of the scenario are a 3D conformal field, or a segment in step-and-shoot IMRT, giving the same MU with a different dose rate (MU/min).24
We use the 4D dose to estimate the dynamic dose:
| (26) |
With Eq. 10, the maximum estimation error is
| (27) |
Next we investigated the dosimetric consequence of phase error. For this set of simulation, Tb = 6 s, Td = 0–60 s, N = 10, K1 = 1, K2 = 4, and K3 = 30 deliveries were used. The simulations performed were as follows: the starting phase for each delivery was an independent uniformly distributed random variable t0(k) ∼ U[0, Tb). For each Td, after K1 (K2, K3) deliveries, the total time in each phase n (T(n)) was tallied, and the deviation from the 4D value T′(n) = KTd/N [Eq. 26] was calculated. The dose difference between the 4D dose and the dynamic dose was calculated as a ratio to ΔDmax:
| (28) |
For simplicity, here we assume that all phase deviations from the 4D value would lead to the maximum dose error. The simulation was repeated 5000 times, and the mean dose difference between the 4D and dynamic doses as a function of K and Td was evaluated.
Here, similar to the special case for the pulsed beam, the effective number of deliveries for each phase could be calculated as
| (29) |
The Poisson estimations of Eqs. 23, 29 were compared with the simulated mean dose difference between the 4D dose and the dynamic dose of Eq. 28.
IMRT delivery time with irregular breathing cycle
To demonstrate the effectiveness of the method established above in a more clinical relevant setting, the delivery time for small segments in IMRT, where 10–15 MU segments in IMRT were observed to lead to large daily variations of the order of 15%–35% by Seco et al.25 was investigated. A simple solution to this problem is to increase the time of delivery of the small segments, or in other words, decrease the dose rate.24 However, since the patient breathing pattern could be irregular and unknown at the time of planning, there was no quantitative study on how the patient breathing change could affect the dose error. For this simulation we use Eq. 28 and the Poisson model [Eqs. 23, 29] to estimate the dose error as a function of length of breathing cycle (Tb = 1–15 s), time of delivery (Td = 1, 6, 10, 30 s), which is effectively changing the dose rate (MU/min) for a given segment with fixed MU, and number of fractions (K = 1, 4, 30).
RESULTS
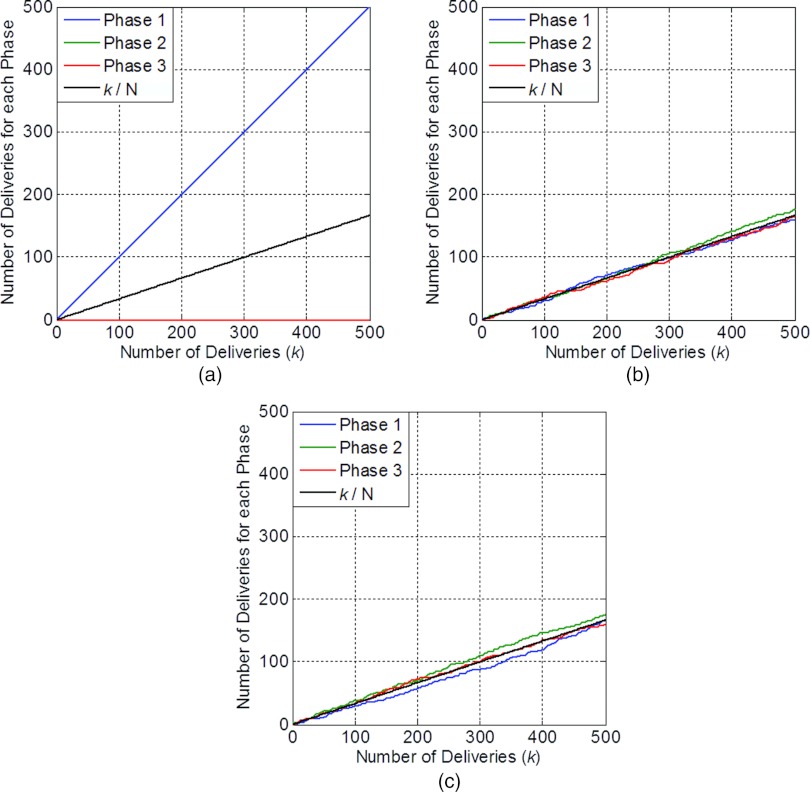
Figure 1 shows the results of one simulation of multiple deliveries for a fixed time t. Figure 1a shows the result for perfect repeated deliveries with fixed t0. In this scenario, for the fixed t we select, E(t) was always delivered to phase 1. Figure 1b shows the result for perfect repeated deliveries with random t0. In this scenario, the number of deliveries to each phase converges to K/N (the black line). Figure 1c shows the result for nonperfect repeated deliveries with random t0. In this scenario, the number of deliveries to each phase also converges to K/N.
Figure 1.
Number of deliveries of E(t) for each phase, as a function of number of deliveries. (a) Perfect repeated deliveries with fixed t0. (b) Perfect repeated deliveries with random t0. (c) Nonperfect repeated deliveries with random t0.
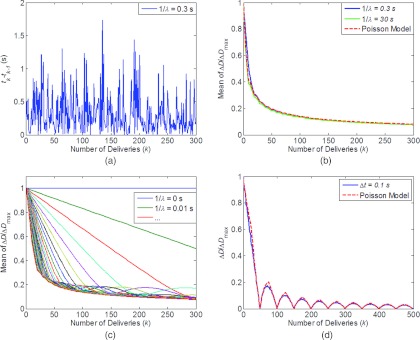
Figure 2 shows the results of the simulations for the pulsed beam. Figures 2a, 2b show the results for 1/λ = 0.3 s. Figure 2a shows the time interval between two consecutive deliveries, which follows the exponential distribution with mean of 0.3 s. Figure 2b shows the mean of ΔD/ΔDmax as a function of the number of deliveries with 1/λ = 0.3 s, 30 s, and calculation of Eq. 19 with ν = K/N. Figure 2c shows the mean of ΔD/ΔDmax as a function of K for different 1/λ. For 1/λ = 0, or if the dose were delivered instantaneously, the repeated delivery does not help to reduce the difference between the 4D dose and the dynamic dose, as the dose was always delivered to only one phase. However, if the interval between two pulses were increased, the estimation error with the 4D dose would decrease as the number of deliveries increased and would quickly converge to the curve shown in Fig. 2b, where the Poisson model predicts the dose error almost perfectly. Note the mean total delivery time is K/λ and increased from 3 s with 1/λ = 0.01 s to 90 s with 1/λ = 0.3 s, and 9000 s with 1/λ = 30 s. Figure 2d shows the special case where instead of following an exponential distribution, Δt was fixed at 0.1 s. In this case, in addition to the general trend of decreasing error with increasing number of deliveries, the 4D dose perfectly predicts the dynamic dose (ΔD = 0) when K = r*Tb/Δt (total delivery time of r*Tb), where r is an integer. The Poisson model overestimates the dose error in this case as the numbers of deliveries for different phases are correlated.
Figure 2.
Mean dose error (ΔD) as a function of number of deliveries (k), for pulsed beam. (a) Time intervals between two deliveries (tk−tk−1), modeled as an exponential distribution with 1/λ = 0.3 s. (b) Mean of (ΔD/ΔDmax) for 1/λ = 0.3 (30) s with different number of deliveries. (c) Mean of (ΔD/ΔDmax) for 1/λ = 0–0.3 s with different number of deliveries. (d) (ΔD/ΔDmax) for Δt = 0.1 s, as a function of number of deliveries. (ΔD/ΔDmax) as calculated with Poisson model in Eqs. 19, 23 were also shown in (b) and (d) with dash lines.
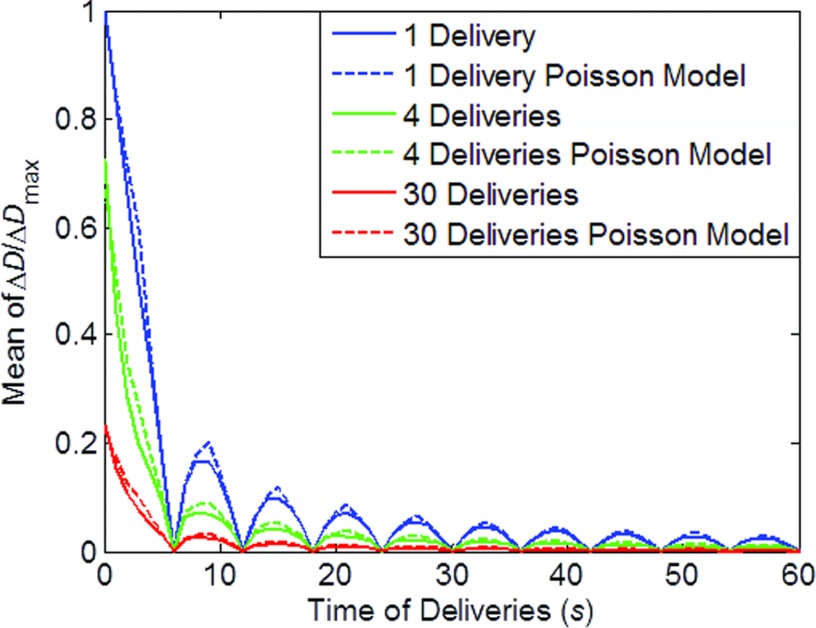
Figure 3 shows the results of the simulations for a continuous beam. As shown in the figure, ΔD decreases with increasing time of delivery. The one delivery curve (0–30 s) is identical to the curve shown in Fig. 2d, suggesting that continuous beam could be viewed as a special case of pulsed beam. With more deliveries, the ΔD was further decreased.
Figure 3.
Mean dose error (ΔD) as a function of time of delivery, for continuous beam. Simulations with 1, 4, 30 deliveries (fractions) along with calculations with Poisson models were shown with dash lines.
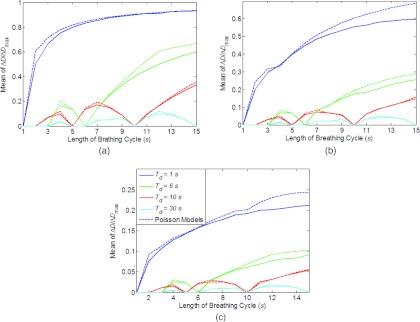
Figure 4 shows the dose error as a function of length of breathing cycle. It can be observed that the dose error increase with Tb when Tb > Td, and could be significantly reduced with longer Td. For a segment with 10 MU, Td = 1 s with 600 MU/min and Td = 10 s with 60 MU/min. With the patient specific ΔDmax, and other information including a generic range of Tb, K, and the maximum allowed dose error, the result in Fig. 4 suggests that it is feasible to calculate the necessary time of delivery for each segment with the Poisson model.
Figure 4.
Mean dose error (ΔD) as a function of length of breathing cycle (Tb), time of delivery (Td), and number of fractions: (a) 1 fraction, (b) 4 fractions, and (c) 30 fractions. Poisson models for each scenario are also shown in dash lines. Legend in (c) valid for (a)–(c).
DISCUSSION
Although dynamic dose would be the representation of delivered dose to patient under ideal conditions, it is not available in most cases. On the other hand, with 4DCT and the mature of deformable registration, the 4D dose calculation has become feasible at planning stage. The purpose of our study was to investigate the relationship between the 4D dose and the dynamic dose, and we have shown that 4D dose is the mean of the dynamic dose, regardless of treatment modality, while the dynamic dose is bounded by Dmax and Dmin, which are derived from the 4D dose. Previous dosimetric studies performed for photon IMRT showed a small (2%–3%) systematic difference between the dynamic dose and the 3D dose,3, 7, 8 up to more than 5% for VMAT,3 and more than 10% for scanning beam proton,9 even with fractionation. These differences are consistent with the systematic difference between the 4D and 3D doses. Although 4D dose represents the mean of the dynamic dose, the delivery condition can and will deviate from the planning condition and thus result in the dynamic dose deviates from the 4D dose. To quantify the dose difference between 4D dose and the dynamic dose, we also established in this work the upper and lower bounds of the dynamic dose by investigating the “worst case scenario” in the 4D dose. Different from previous works, the determination of the bounds does not require repeated dose calculation, and therefore enables patient specific quantification of the motion induced dose uncertainty, which was not feasible with previous techniques. With the establishment of Dmax and Dmin, we also able to investigate the relationship between the number of deliveries and/or delivery time with the dose error, for both pulsed and continuous beams. For pulsed beam, without calculating the patient dose, the result shown in Fig. 2b and Fig. 3 are consistent with results for scanning proton repainting studies (Figs. 4 and 5 in Seco et al.13) and IMRT studies (Fig. 4 in Seco et al.25), respectively. These results confirm the validity and generality of our study. For both pulsed and continuous beams, the estimation error using the 4D dose, or the interplay effect, decreased quickly with increased treatment time and/or number of deliveries. For continuous beam and pulsed beam with a constant interval between pulses, the error is also a function of the breathing period.
The effective number of deliveries (v) for each phase was modeled as Poisson processes, and as a result the estimation error or interplay effect can be written as an analytical function of v [Eq. 19] and easily calculated. The advantage of using the Poisson model is the ability to predict the dose error without repeated calculation of dose to patient with multiple deliveries. For continuous beam, although it is easy to analytically calculate ΔD of Eq. 28 for K = 1 (not shown in this work), it is more natural to use a Poisson process to estimate ΔD with multiple deliveries, with which continuous beam can be viewed as a special case of pulsed beam. As shown in Figs. 23, Poisson process nicely model the random pulsed beam, and the fractionation of the continuous beam. It also agrees reasonable well with the continuous beam after considering the number of effective deliveries within a breathing cycle. For step and shoot IMRT, we showed in Fig. 4 that it is feasible to calculate the necessary deliver time for each segment to achieve a maximum allowed dose error. If this method, along with the 4D dose calculation and the bounds, were integrated in the treatment planning system, the motion induced dose uncertainty can then easily be quantified and minimized at the time of treatment planning for any patient with 4DCT studies. While the current work focused on the physics aspect of our method, the clinical and implementation aspect of the method will be discussed in a follow-up paper.
Although the magnitude of motion is not explicitly included in our formulation, it is obvious that with no patient motion, the dynamic (and 4D) dose will collapse to the 3D static dose. However, with a larger magnitude of tumor motion, the dose difference between different phases would increase, which may lead to increased difference between dynamic (and 4D) and 3D static doses.4, 12 Gating,26 for example, is one way to reduce the effective magnitude of tumor motion. With the establishment of the maximum difference between dynamic dose and 4D dose in Eq. 10, it is possible not only to optimize the 4D dose to ensure coverage and normal tissue sparing but also to minimize the ΔDmax and thus reduce the patient dose uncertainty due to the interplay effect. Although the difference between the 4D and 3D doses was fairly small (2%-3%) and regardless of the tumor motion for most IMRT and VMAT treatments (and 3D static dose has often been used to approximate the 4D dose and the dynamic dose),7, 8, 10 4D optimization with minimizing ΔDmax for IMRT could still potentially further reduce the dose to normal tissue and improve target coverage.18, 19 4D optimization and dose calculation should be the preferred technique for scanning beam proton because of the larger error with 3D static dose calculation.4, 9, 13, 20, 21 However, the optimization process is highly modality dependent and therefore is not discussed in this paper.
We assume there were no residual motions within each phase of the 4DCT and that the dose calculation of the 4D dose was accurate within each phase. These assumptions are patient dependant and heavily depend on the image quality of the 4DCT. Therefore it is important to improve the image quality and reduce artifacts in 4DCT (Refs. 27 and 28) to improve the 4D dose calculation accuracy. Although we have included breathing pattern change in our results, we assume the planning 4DCT being a good representation of the patient anatomy and breathing amplitude throughout the treatment, which may not be true and repeated volumetric images may still be necessary to detect anatomy changes. Biological effect of the dose average of 4D dose, which was done in fractionated treatment, has not been considered, and may require further investigation.
CONCLUSION
Dynamically accumulated dose will converge to the 4D accumulated dose after multiple deliveries, regardless of treatment modality and delivery properties. Bounds of the dynamic dose were established with 4D dose calculation, and a Poisson model was developed to quantify the motion induced dose uncertainties as a function of time.
ACKNOWLEDGMENTS
The authors thank the Department of Scientific Publications at MD Anderson Cancer Center for editorial review of this paper. MD Anderson Cancer Center is supported by the National Institutes of Health (NIH) through Grant No. CA16672.
References
- Bert C., Grozinger S. O., and Rietzel E., “Quantification of interplay effects of scanned particle beams and moving targets,” Phys. Med. Biol. 53, 2253–2265 (2008). 10.1088/0031-9155/53/9/003 [DOI] [PubMed] [Google Scholar]
- Bortfeld T., Jiang S. B., and Rietzel E., “Effects of motion on the total dose distribution,” Semin. Radiat. Oncol. 14, 41–51 (2004). 10.1053/j.semradonc.2003.10.011 [DOI] [PubMed] [Google Scholar]
- Court L. E., Seco J., Lu X. Q., Ebe K., Mayo C., Ionascu D., Winey B., Giakoumakis N., Aristophanous M., Berbeco R., Rottman J., Bogdanov M., Schofield D., and Lingos T., “Use of a realistic breathing lung phantom to evaluate dose delivery errors,” Med. Phys. 37, 5850–5857 (2010). 10.1118/1.3496356 [DOI] [PubMed] [Google Scholar]
- Lambert J., Suchowerska N., McKenzie D. R., and Jackson M., “Intrafractional motion during proton beam scanning,” Phys. Med. Biol. 50, 4853–4862 (2005). 10.1088/0031-9155/50/20/008 [DOI] [PubMed] [Google Scholar]
- Yu C. X., Jaffray D. A., and Wong J. W., “The effects of intra-fraction organ motion on the delivery of dynamic intensity modulation,” Phys. Med. Biol. 43, 91–104 (1998). 10.1088/0031-9155/43/1/006 [DOI] [PubMed] [Google Scholar]
- Litzenberg D. W., Hadley S. W., Tyagi N., Balter J. M., Ten Haken R. K., and Chetty I. J., “Synchronized dynamic dose reconstruction,” Med. Phys. 34, 91–102 (2007). 10.1118/1.2388157 [DOI] [PubMed] [Google Scholar]
- Jiang S. B., Pope C., Al Jarrah K. M., Kung J. H., Bortfeld T., and Chen G. T., “An experimental investigation on intra-fractional organ motion effects in lung IMRT treatments,” Phys. Med. Biol. 48, 1773–1784 (2003). 10.1088/0031-9155/48/12/307 [DOI] [PubMed] [Google Scholar]
- Rao M., Wu J., Cao D., Wong T., Mehta V., Shepard D., and Ye J., “Dosimetric impact of breathing motion in lung stereotactic body radiotherapy treatment using image-modulated radiotherapy and volumetric modulated arc therapy,” Int. J. Radiat. Oncol., Biol., Phys. 83, e251–e256 (2012). Epub Feb. 24, 2012. 10.1016/j.ijrobp.2011.12.001 [DOI] [PubMed] [Google Scholar]
- Kraus K. M., Heath E., and Oelfke U., “Dosimetric consequences of tumour motion due to respiration for a scanned proton beam,” Phys. Med. Biol. 56, 6563–6581 (2011). 10.1088/0031-9155/56/20/003 [DOI] [PubMed] [Google Scholar]
- Bortfeld T., Jokivarsi K., Goitein M., Kung J., and Jiang S. B., “Effects of intra-fraction motion on IMRT dose delivery: Statistical analysis and simulation,” Phys. Med. Biol. 47, 2203–2220 (2002). 10.1088/0031-9155/47/13/302 [DOI] [PubMed] [Google Scholar]
- Papanikolaou N., Battista J. J., Boyer A. L., Kappas C., Klein E., Mackie T. R., Sharpe M., and Dyk J. V., AAPM Report No. 85: Tissue Inhomogeneity Corrections for Megavoltage Photon Beams (AAPM, College Park, MD, 2004).
- Evans P. M., Coolens C., and Nioutsikou E., “Effects of averaging over motion and the resulting systematic errors in radiation therapy,” Phys. Med. Biol. 51, N1–N7 (2006). 10.1088/0031-9155/51/1/N01 [DOI] [PubMed] [Google Scholar]
- Seco J., Robertson D., Trofimov A., and Paganetti H., “Breathing interplay effects during proton beam scanning: Simulation and statistical analysis,” Phys. Med. Biol. 54, N283–N294 (2009). 10.1088/0031-9155/54/14/N01 [DOI] [PubMed] [Google Scholar]
- Keall P. J., Joshi S., Vedam S. S., Siebers J. V., Kini V. R., and Mohan R., “Four-dimensional radiotherapy planning for DMLC-based respiratory motion tracking,” Med. Phys. 32, 942–951 (2005). 10.1118/1.1879152 [DOI] [PubMed] [Google Scholar]
- Starkschall G., Britton K., McAleer M. F., Jeter M. D., Kaus M. R., Bzdusek K., Mohan R., and Cox J. D., “Potential dosimetric benefits of four-dimensional radiation treatment planning,” Int. J. Radiat. Oncol., Biol., Phys. 73, 1560–1565 (2009). 10.1016/j.ijrobp.2008.12.024 [DOI] [PubMed] [Google Scholar]
- Paganetti H., Jiang H., and Trofimov A., “4D Monte Carlo simulation of proton beam scanning: Modelling of variations in time and space to study the interplay between scanning pattern and time-dependent patient geometry,” Phys. Med. Biol. 50, 983–990 (2005). 10.1088/0031-9155/50/5/020 [DOI] [PubMed] [Google Scholar]
- Bert C. and Rietzel E., “4D treatment planning for scanned ion beams,” Radiat. Oncol. 2, 24 (2007). 10.1186/1748-717X-2-24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X., Wang X., Li Y., and Zhang X., “A 4D IMRT planning method using deformable image registration to improve normal tissue sparing with contemporary delivery techniques,” Radiat. Oncol. 6, 83 (2011). 10.1186/1748-717X-6-83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nohadani O., Seco J., and Bortfeld T., “Motion management with phase-adapted 4D-optimization,” Phys. Med. Biol. 55, 5189–5202 (2010). 10.1088/0031-9155/55/17/019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knopf A. C., Hong T. S., and Lomax A., “Scanned proton radiotherapy for mobile targets-the effectiveness of re-scanning in the context of different treatment planning approaches and for different motion characteristics,” Phys. Med. Biol. 56, 7257–7271 (2011). 10.1088/0031-9155/56/22/016 [DOI] [PubMed] [Google Scholar]
- Li Y., Zhang X., Li X., Pan X., and Mohan R., “Evaluating 4D interplay effects for proton scanning beams in lung cancers,” Med. Phys. 36, 2579 (2009). 10.1118/1.3182465 [DOI] [Google Scholar]
- Zenklusen S. M., Pedroni E., and Meer D., “A study on repainting strategies for treating moderately moving targets with proton pencil beam scanning at the new Gantry 2 at PSI,” Phys. Med. Biol. 55, 5103–5121 (2010). 10.1088/0031-9155/55/17/014 [DOI] [PubMed] [Google Scholar]
- Crow E. L., “The Mean Deviation of the Poisson Distribution,” Biometrika 45, 556–562 (1958). 10.1093/biomet/45.3-4.556 [DOI] [Google Scholar]
- Court L., Wagar M., Bogdanov M., Ionascu D., Schofield D., Allen A., Berbeco R., and Lingos T., “Use of reduced dose rate when treating moving tumors using dynamic IMRT,” J. Appl. Clin. Med. Phys. 12, 3276 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seco J., Sharp G. C., Turcotte J., Gierga D., Bortfeld T., and Paganetti H., “Effects of organ motion on IMRT treatments with segments of few monitor units,” Med. Phys. 34, 923–934 (2007). 10.1118/1.2436972 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bert C., Gemmel A., Saito N., and Rietzel E., “Gated irradiation with scanned particle beams,” Int. J. Radiat. Oncol., Biol., Phys. 73, 1270–1275 (2009). 10.1016/j.ijrobp.2008.11.014 [DOI] [PubMed] [Google Scholar]
- Starkschall G., Desai N., Balter P., Prado K., Luo D., Cody D., and Pan T., “Quantitative assessment of four-dimensional computed tomography image acquisition quality,” J. Appl. Clin. Med. Phys. 8, 2362 (2007). 10.1120/jacmp.v8i3.2362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noel C. E. and Parikh P. J., “Effect of mid-scan breathing changes on quality of 4DCT using a commercial phase-based sorting algorithm,” Med. Phys. 38, 2430–2438 (2011). 10.1118/1.3574872 [DOI] [PubMed] [Google Scholar]