Table 2. Comparison of training error vs. actual error of a rule in model selection for different values.

	noise = 0		noise = 0.1		noise = 0.3		noise = 0.4
	selected	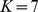	selected		selected		selected
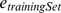
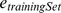
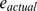
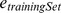
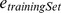
1	0.12	0.41	0.17	0.28	0.36	0.51	0.26	0.29
3	0.05	0.26	0.03	0.22	0.34	0.62	0.29	0.29
5	0.16	0.28	0.03	0.25	0.23	0.33	0.25	0.28
7	0.04	0.24	0.03	0.22	0.23	0.33	0.32	0.37
9	0.12	0.27	0.07	0.25	0.25	0.29	0.24	0.33

This table indicates the error of a rule as obtained from the training data and the corresponding actual state transition error for different noise levels and different values of , where is the total mixtures in a Bernoulli mixture model. If lower training error also corresponds to lower actual rule error then training error can be taken as a good measure to assess the error of a rule and hence it can be used as a criterion for selecting . However, low training error corresponding to high rule error indicates over fitting. The results are shown for the 10 nodes network, for node 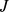with indegree 9. The value of 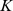for which the training error is minimum is chosen as the final value of this parameter. The lowest error is highlighted for each column. The strategy works quite well for low noise levels and reasonably well for higher noise levels. The plot for noise levels 0 and 0.4 is also illustrated in Figure 4.