Estimating diagnostic accuracy of raters without a gold standard by exploiting a group of experts

Abstract

In diagnostic medicine, estimating the diagnostic accuracy of a group of raters or medical tests relative to the gold standard is often the primary goal. When a gold standard is absent, latent class models where the unknown gold standard test is treated as a latent variable are often used. However, these models have been criticized in the literature from both a conceptual and a robustness perspective. As an alternative, we propose an approach where we exploit an imperfect reference standard with unknown diagnostic accuracy and conduct sensitivity analysis by varying this accuracy over scientifically reasonable ranges. In this article, a latent class model with crossed random effects is proposed for estimating the diagnostic accuracy of regional obstetrics and gynaecological (OB/GYN) physicians in diagnosing endometriosis. To avoid the pitfalls of models without a gold standard, we exploit the diagnostic results of a group of OB/GYN physicians with an international reputation for the diagnosis of endometriosis. We construct an ordinal reference standard based on the discordance among these international experts and propose a mechanism for conducting sensitivity analysis relative to the unknown diagnostic accuracy among them. A Monte-Carlo EM algorithm is proposed for parameter estimation and a BIC-type model selection procedure is presented. Through simulations and data analysis we show that this new approach provides a useful alternative to traditional latent class modeling approaches used in this setting.

1 Introduction

The motivation for this statistical research comes from the Physician Reliability Study (PRS) (Schliep et al., 2012) that investigated the diagnosis of endometriosis for various types of physicians by using different combinations of clinical information. Endometriosis is a gynecological medical condition in which cells from the lining of the uterus appear and flourish outside the uterine cavity, most commonly on the ovaries. The diagnosis of endometriosis can be complicated and there is no consensus in the field on what constitutes the gold standard (e.g., Brosens and Brosens, 2000). Of interest in the PRS is estimating the diagnostic accuracy of a group of regional obstetrics and gynecological (OB/GYN) physicians (R-OB/GYNs) in terms of their endometriosis diagnosis. The R-OB/GYNs were presented with digital images of the uterus and adnexal structure of participants that were taken during laparoscopies and were asked to make a diagnosis of endometriosis. Since these R-OB/GYNs see patients daily and are affiliated with the same medical center, an assessment of their diagnostic accuracy can help the medical center in designing specific training programs to improve their diagnosis.

Diagnostic accuracy of raters or medical tests are of considerable interest in many public health and biomedical fields (Zou, McClish, and Obuchowski, 2002; Pepe, 2003; Hui and Walter, 1980). The estimation of diagnostic accuracy is straightforward when the true disease status is known. In many cases such as for endometriosis, however, a gold standard is not available. Methods have been proposed to estimate diagnostic accuracy without a gold standard using latent class models for which the true disease status is considered to be a latent variable (Hui and Walter, 1980; Hui and Zhou, 1998). Qu, Tan, and Kutner (1996) proposed a random-effects latent class model that introduces conditional dependence between tests with normally distributed random effects. Albert et al. (2001) proposed a latent class model with a finite mixture structure to account for dependence between tests. More recently, it has been shown that latent class models for estimating diagnostic accuracy may be problematic in many practical situations (Albert and Dodd, 2004; Pepe and Janes, 2006). Specifically, Albert and Dodd (2004) showed that with a small number of binary tests, estimates of diagnostic accuracy are biased under a misspecified dependence structure; yet in many situations it is nearly impossible to distinguish between models with different dependence structures from observed data.

Between the two extremes of no gold standard on anyone and a gold standard on all individuals, there are situations where a gold standard does not exist but some imperfect information is available. When there is no gold standard, the best available reference tests can be employed to help the estimation of diagnostic accuracy of new tests. Those best available reference tests may themselves be subject to small error, and therefore are called imperfect reference standard. In the motivating PRS example, there are diagnostic results on the same subjects from a group of international expert (IE) OB/GYN physicians. These IEs all had directed specialized training in laparoscopic surgery, accrued extensive clinical and research experience in diagnosing and treating endometriosis, and have international reputations in the field. A scatterplot of the correlation between the IE and R-OB/GYN ratings is included in Web Appendix A of the web-based supplementary materials. In this paper, we propose new methodology to estimate the R-OB/GYNs’ diagnostic accuracy by exploiting the IEs’ diagnostic results in the PRS.

Valenstein (1990), Begg (1987), and Qu and Hadgu (1998) have discussed the bias in estimating diagnostic accuracy using an imperfect reference standard. Using both analytical and simulation techniques, Albert (2009) showed that, with the aid of an imperfect reference standard with high sensitivity and specificity, inferences on diagnostic accuracy are robust to misspecification of the conditional dependence between tests. However, this approach assumes that the diagnostic accuracy of the imperfect reference standard is known or can be estimated from other data sources. In some cases, no gold standard exists and it is impossible to obtain estimates of the diagnostic accuracy of the imperfect reference standard relative to the gold standard from other studies. In this situation, we show how multiple expert raters or more definitive tests can be used along with a sensitivity analysis to estimate the diagnostic accuracy of other raters or tests.

Our proposed approach for estimating the average diagnostic accuracy among R-OB/GYNs makes use of the latent class model as in the aforementioned literature for models without a gold standard. Since each physician examines each subject in the PRS, we develop an approach where R-OB/GYNs are random and crossed with subjects. To exploit the IEs’ diagnostic results, we construct an ordinal composite imperfect reference standard from the individual diagnostic results of the IEs. We first assume that we know the diagnostic accuracy of the imperfect reference standard and proceed with estimating the diagnostic accuracy of the R-OB/GYNs. In this step, the value of the diagnostic accuracy of the imperfect reference standard is chosen such that the corresponding posterior probability of the latent disease status given the observed ordinal reference standard is reasonable. We then vary this choice widely within a scientifically sensible range of the posterior probabilities in order to assess the robustness of the estimated diagnostic accuracy of the R-OB/GYNs. To handle the computational challenge arising from the crossed random effects, we develop a Monte-Carlo EM algorithm for parameter estimation. We investigate the robustness of the proposed latent class model with respect to the misspecification of the dependence structure between tests. We show that, without the imperfect reference standard (i.e., IE reviewers), estimates of diagnostic parameters are biased under a misspecified dependence structure. Moreover, the model selection criterion (Ibrahim, Zhu, and Tang, 2008) has difficulty distinguishing the various competing models. However, with the aid of the imperfect ordinal standard, (i) estimates of diagnostic accuracy are nearly unbiased, even when the dependence structure between the R-OB/GYN tests is misspecified or when the assumed diagnostic accuracy of the imperfect reference standard deviates from the truth in a reasonable way and (ii), we are able to distinguish between competing models for the dependence between R-OB/GYNs.

In section 2, we propose a latent class modeling approach for estimating the diagnostic accuracy of the R-OB/GYNs that exploits the IEs by constructing an ordinal reference standard. In Section 3, we investigate the bias from misspecifying the random effects structure with and without the use of the imperfect reference standard. In Section 4, we apply the proposed model to data from the PRS in the diagnosis of endometriosis. A discussion follows in Section 5.

2 Methods

2.1 Random-effects latent class model without a gold or imperfect reference standard

Let Y_ij denote the binary diagnostic result of endometriosis (Y_ij = 1(0) for having (not having) endometriosis) for the ith subject from the jth R-OB/GYN, i = 1, 2, · · ·, I and j = 1, 2, · · ·, J. In the PRS, we consider 79 subjects who had complete diagnoses from 8 R-OB/GYNs and 4 IEs; thus, I = 79 and J = 8. We denote D_i as the true disease status of the ith subject. Due to the lack of a gold or imperfect reference standard for endometriosis, we model D_i as a binary latent variable. In the PRS, the eight R-OB/GYNs are chosen from a group of regional physicians, and interest is on estimating the average sensitivity and specificity across the population of these physicians, rather than the eight physician-specific sensitivities and specificities themselves. Therefore, we consider the following model with two crossed random effects:

$$P(Y_{ij}=1\mid D_i=d_i,b_i,c_j)=\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right),{\sigma }_{d_i},{\tau }_{d_i}>0,$$ (1)

where b_i is the subject-specific random effect with probability density distribution (p.d.f.) g₁(x), c_j is the rater-specific random effect with p.d.f. g₂(x), and the three unobserved latent variables D_i, b_i, and c_j are assumed to be independent of each other. Let π_di = P(D_i = d_i) and note π₁ is the prevalence of endometriosis in the population.

Contrast to the latent class models with a Gaussian random effect model in Qu, Tan and Kutner (1996) and Albert (2001), where the rater sensitivity and specificity were treated as fixed effects, (1) can be used to estimate the average sensitivity and specificity across the population of regional physicians as follows: $S_e=\mathrm{\Phi }({\beta }_1/\sqrt{1+{\sigma }_1^2+{\tau }_1^2})$ and $S_p=\mathrm{\Phi }(-{\beta }_0/\sqrt{1+{\sigma }_0^2+{\tau }_0^2})$ under the normality assumption of b_i and c_j. These expressions are obtained by integrating out both subject- and rater-level random effects. For notational brevity, we will simply call them sensitivity and specificity in the remainder of the paper. In addition to the normality assumption on the random effects, we consider the case where g₁(x) and g₂(x) are two-group mixture normal distribution with p.d.f.:

$$g_m(x)={\lambda }_m\phi (x;{\mu }_{1m,}{\nu }_{1m}^2)+(1-{\lambda }_m)\phi (x;{\mu }_{2m},{\nu }_{2m}^2),m=1,2,$$ (2)

where λ_m is the probability in the first group, 0 ≤ λ_m ≤ 1, and φ(x; μ, ν²) is the p.d.f. of a normal distribution with mean μ and variance ν² (Albert et al., 2001). For model identification, we assume λ_mμ_1m + (1 − λ_m)μ_2m = 0, ${\lambda }_m^2{\nu }_{1m}^2+{(1-{\lambda }_m)}^2{\nu }_{2m}^2+2{\lambda }_m^2{\mu }_{1m}=1$ and μ_1m < μ_2m. Similar to the Gaussian random effects model with crossed random effects, the model-based estimates of sensitivity and specificity can be obtained by marginalizing over the two-group mixture models.

The likelihood of (1) is complicated by the two crossed random effects b_i and c_j. Let Y_i = (Y_i1, Y_i2, · · ·, Y_iJ )′ be the J dichotomous rating results on the ith subject. Also, let $Y=(Y_1^{\prime },Y_2^{\prime },\cdots ,Y_I^{\prime })$, D = (D₁, D₂, · · ·, D_I) and θ be the vector of unknown parameters β_di, σ_di, τ_di, π_di and the unknown parameters in g_i(x). Then, the likelihood of the proposed model (1) is given by

$$L(\theta \mid y)=\int \cdots \int \sum _{d_1=0}^1\cdots \sum _{d_I=0}^1[\prod _{i=1}^I\prod _{j=1}^J{\left\{\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right)\right\}}^{y_{ij}}\times {\left\{1-\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right)\right\}}^{1-y_{ij}}]\prod _{i=1}^I{\pi }_{d_i}{g}_1(b_i){\text{d}b}_i\prod _{j=1}^J{g}_2(c_j){\text{d}c}_j.$$ (3)

The likelihood (3) involves high-dimensional integration and summation, which is difficult to evaluate by numerical approximation. As a consequence, a Monte-Carlo EM algorithm is presented in Web Appendix B of the web-based supplementary materials to obtain the maximum-likelihood estimation of (3).

2.2 Random-effects latent class model with an ordinal imperfect reference standard

In addition to the eight R-OB/GYNs, four IEs provided diagnoses of endometriosis for each subject in the PRS. These IEs are well-known OB/GYN physicians in the field and are expected to have better diagnostic accuracy than other physicians. Although a gold standard does not exist for endometriosis, the diagnostic results from these IEs can be used to construct an imperfect reference standard to improve the estimation of average diagnostic accuracy of the R-OB/GYNs. Specifically, an ordinal imperfect reference standard can be constructed based on the multiple IE binary ratings. Generally, suppose there are L binary IE ratings ${\stackrel{\sim }{T}}_i^{(l)}$ for the ith subject, l = 1, · · ·, L. We propose to use the sum of those binary ratings as the imperfect reference standard $T_i={\sum }_{l=1}^L{\stackrel{\sim }{T}}_i^{(l)}$, where T_i takes values 0, 1, · · ·, L. In the PRS, L is equal to 4. Letting T = (T₁, T₂, · · ·, T_I), the likelihood of the observed rating results Y and imperfect reference standard T is

$$L(\theta \mid y,t)=\sum _{d_1=0}^1\cdots \sum _{d_I=0}^1\left\{P(Y=y\mid T=t,D=d)\prod _{i=1}^I{S}_{t_i\mid d_i}^T\prod _{i=1}^I{\pi }_{d_i}\right\},$$ (4)

where $S_{t_i\mid d_i}^T=P(T_i=t_i\mid D_i=d_i)$ characterizes the diagnostic accuracy of the imperfect reference standard relative to the true disease status. In this section, we will assume $S_{t_i\mid d_i}^T$ is known. However, for endometriosis there is no established gold standard available for estimating these quantities. When no gold standard exists, we propose a methodological approach for conducting a sensitivity analysis in section 2.3.

To incorporate the information of the imperfect reference standard, we consider the model

$$P(Y_{ij}=1\mid T_i=t_i,D_i=d_i,b_i,c_j)=\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right),{\sigma }_{d_i},{\tau }_{d_i}>0,$$ (5)

where we make the assumption that the observed ratings do not depend on the imperfect reference standard if the true disease status is available. This is a natural assumption which is usually true in practice. The assumption can be relaxed by allowing β to depend on T_i (i.e., replacing β_di with β_diTi in (5)) or by introducing dependence between the Y_ij’s and T_i’s through a shared random effect (see Web Appendix F). The corresponding likelihood is given by

$$L(\theta )=\int \cdots \int \sum _{d_1=0}^1\cdots \sum _{d_I=0}^1[\prod _{i=1}^I\prod _{j=1}^J{\left\{\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right)\right\}}^{y_{ij}}\times {\left\{1-\mathrm{\Phi }\left({\beta }_{d_i}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right)\right\}}^{1-y_{ij}}]\prod _{i=1}^I{S}_{t_i\mid d_i}^T{\pi }_{d_i}{g}_1(b_i){\text{d}b}_i\prod _{j=1}^J{g}_2(c_j){\text{d}c}_j.$$ (6)

A Monte-Carlo EM algorithm is used to obtain maximum likelihood estimates of β_di, σ_di and τ_di, d_i = 0 or 1, by maximizing (6).

There are special cases of the proposed methodology. When $S_{L\mid 1}^T=S_{0\mid 0}^T=1$, it reduces to the case in which the true disease status is observed. For diagnosing endometriosis in the PRS, it corresponds to the scenario where all four IEs report positive results if the subject has endometriosis and they all report negative results if the subject does not (i.e., IEs have perfect classifications). When $S_{t_i\mid 1}^T=S_{t_i\mid 0}^T=1/(L+1)$ for t_i = 0, 1, · · ·, L, the imperfect reference standard (IEs) adds no additional information, and the approach reduces to a latent class model without a gold standard for the R-OB/GYNs alone.

2.3 Sensitivity study of the ordinal imperfect reference standard

As stated in Section 2.2, we construct the imperfect reference standard T by using the diagnostic results from the four IEs in the PRS. In this application, we do not know the diagnostic accuracy of the IEs and, consequently, do not know the diagnostic accuracy of the constructed imperfect reference standard. Hence, we discuss how we conduct sensitivity analysis for diagnostic accuracy estimation of the R-OB/GYNs by varying the diagnostic accuracy of the imperfect reference standard over a wide range of reasonable values. In particular, we assume the following polychotomous logit model,

$$S_{t_i\mid d_i}^T=\frac{exp({\gamma }_0+{\gamma }_1{t}_i+{\gamma }_2{t}_i^2)}{1+{\displaystyle \sum _{h=0}^3}exp({\gamma }_0+{\gamma }_{1}h+{\gamma }_2{h}^2)},t_i=0,1,\cdots ,3,$$ (7)

and a symmetrically defined $S_{t_i\mid 0}^T:S_{t_i\mid 0}^T=S_{4-t_i\mid 1}^T$. Note here that $S_{4\mid 1}^T=1-{\displaystyle \sum _{t=0}^3}{S}_{t\mid 1}^T$. Denoting $S_{d_i\mid t_i}^D=P(D_i=d_i\mid T_i=t_i)$ , then by Bayes rule,

$$S_{d_i\mid t_i}^D=\frac{S_{t_i\mid d_i}^T{\pi }_{d_i}}{{\displaystyle \sum _{d=0,1}}{S}_{t_i\mid d_i}^T{\pi }_d},$$ (8)

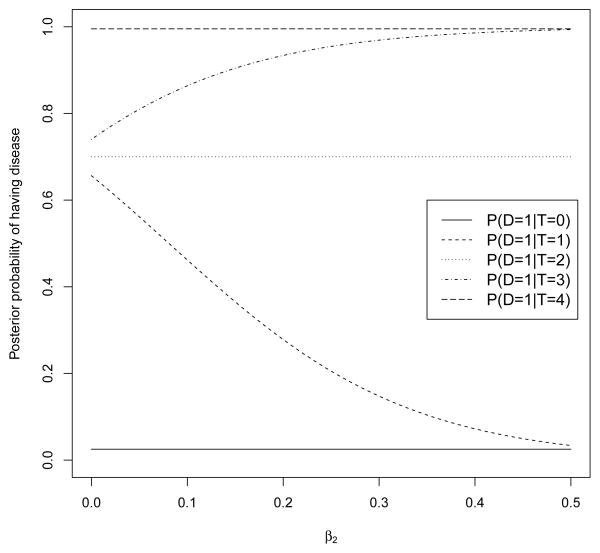
which characterizes the posterior probability of disease given the observed imperfect reference standard. We focus on the sum of the IE ratings, rather than their individual values, since this provides a simple and intuitive approach for sensitivity analysis that does not require the specification of the dependence structure between the multiple IE ratings. With regard to choosing parameter of (7), we suggest that parameters be chosen so that $S_{1\mid 4}^D$ and $S_{0\mid 0}^D$ are both close to zero (i.e., the probability that a woman is truly negative (positive) for endometriosis but all IEs independently diagnose her as positive (negative) is reasonably assumed to be zero). Figure 1 shows posterior probability of having disease for different values of γ₂ in (8) where γ₀ = −4.5, γ₁ = 0.1 and π₁ = 0.70. The impact of the change of γ₂ on the estimation of the diagnostic accuracy of the regional physicians is examined in both the simulation and application sections.

Figure 1.

Posterior probability of having disease for different values of γ₂ in equations (8) and (7). γ₀ and γ₁ are assumed known with γ₀ = −4.5, γ₁ = 0.1.

In the simulation and discussion sections as well as the web-based supplementary materials, we show that the proposed approach for exploiting the IEs and conducting sensitivity analysis is robust to (i) the assumed dependence structure among the R-OB/GYN ratings and (ii) the exchangeability assumption implicit in using the sum of the IE ratings as an imperfect reference standard.

3 Simulation Studies

The simulation datasets were generated from the latent class models with random effects that follow mixture normal distribution (“true model”) and were fit to models with either normal or mixture normal random effects (“working model”). All simulations were conducted with 500 replications, each with 100 subjects (I = 100). The average sensitivity and specificity and the disease prevalence over 500 replications and their standard deviations are shown with five (J = 5) or ten (J = 10) raters in Table 1.

Table 1.

Simulation results for sensitivity and specificity under the scenarios (A) with no gold or imperfect reference standard, (B) with a correctly specified imperfect reference standard (γ₀ = −4.5, γ₁ = 0.1, γ₂ = 0.2 in equations (7) and (8), and (C) with an incorrectly specified imperfect reference standard (γ₀ = −4.5, γ₁ = 0.1, γ₂ = 0.1 equations (7) and (8). The random effects of the true models follow mixture normal (MixN) distribution. The averages of estimates (standard errors) and the percentage of selecting true model by IC_H(0),Q are presented. The true sensitivity, specificity and disease prevalence are S_e = 0.88, S_p = 0.87, and π₁ = 0.7, respectively.

Number of tests	Working random effects distribution	Ŝe(se)	Ŝp(se)	π̂1(se)	Rate of selecting true model
(A)
5	Normal	0.81(0.053)	0.81(0.039)	0.78(0.054)	55%
	MixN	0.88(0.055)	0.86(0.059)	0.70(0.057)
10	Normal	0.82(0.046)	0.83(0.047)	0.77(0.052)	52%
	MixN	0.88(0.053)	0.87(0.061)	0.70(0.063)
(B)
5	Normal	0.87(0.055)	0.87(0.045)	0.70(0.056)	95%
	MixN	0.88(0.060)	0.86(0.062)	0.69(0.053)
10	Normal	0.88(0.051)	0.87(0.048)	0.70(0.048)	96%
	MixN	0.88(0.063)	0.88(0.062)	0.70(0.059)
(C)
5	Normal	0.89(0.064)	0.87(0.055)	0.70(0.047)	89%
	MixN	0.88(0.058)	0.86(0.063)	0.70(0.038)
10	Normal	0.88(0.041)	0.87(0.049)	0.70(0.054)	91%
	MixN	0.88(0.060)	0.87(0.068)	0.70(0.055)

Table 1(A) presents the results when there is no gold or imperfect reference standard. The results show that, with no help of a gold or imperfect reference standard, there is sizable bias in estimation when the random effects (both between subjects and between raters) in the true model follow mixture normal distributions and in the working model follow normal distributions. The averages of estimated mean sensitivity and specificity are both 0.81 for 5 raters, and 0.82 and 0.83 for 10 raters, respectively, compared to the true sensitivity of 0.88 and true specificity of 0.87. Moreover, we are unable to distinguish between the true and the misspecified models by using model selection criterion IC_H(0),Q (Ibrahim, Zhu, and Tang, 2008); the percentages that IC_H(0),Q selected the true random effects structure are just sightly above 50% (55% for 5 raters; 52% for 10 raters). These results are consistent with Albert and Dodd (2004) who showed that for fixed rater-specific diagnostic accuracy, estimation is sensitive to misspecification of the random effects distribution, yet it is difficult to distinguish between random effects distributions using the observed data.

In the case when an ordinal imperfect reference standard is used and the diagnostic accuracy of the imperfect reference standard is known, we assume that the imperfect reference standard T_i is ordinal taking values 0, 1, · · ·, 4, and that the true disease status D_i remained binary taking 0 (no disease) or 1 (disease). The imperfect reference standard was generated under (7) with γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.2. The corresponding posterior disease probabilities $S_{1\mid t_i}^D$ given t_i = 0, 1, 2, 3, 4, when π₁ = 0.70, were 0.02, 0.28, 0.70, 0.93, and 1.00, respectively. Table 1(B) shows that, with the aid of the imperfect reference standard that has known diagnostic accuracy, the proposed latent class model is robust in estimating sensitivity, specificity, and disease prevalence when the random effect distributions are mis-specified. More specifically, when the true model random effects distributions are mixture normal distributions and the working model assumes normal random effects distributions, the estimates are nearly unbiased with the average estimated sensitivities at 0.87 for 5 raters and 0.88 for 10 raters, and the average estimated specificities both at 0.87. In addition, we are able to distinguish between the true and misspecified models by using model selection criterion IC_H(0),Q; the percentages that IC_H(0),Q selected the true random effects structure are about 90% or above in both the 5- and 10-rater cases. With the imperfect reference standard, there is also no observed efficient loss under misspecified random effect distributions relative to the correct distributions.

The results in Table 1(B) show how incorporating an imperfect reference standard improves the robustness of the estimation, assuming that we know the diagnostic accuracy of it. However, in most practice situations, we do not know the diagnostic accuracy of the imperfect reference standard. In the PRS, we construct the imperfect reference standard from four IEs, but have no information about the diagnostic accuracy of this imperfect reference standard. Thus, it is of interest to investigate the robustness of the proposed latent class model to reasonable misspecification of the diagnostic accuracy of the imperfect reference standard. For this reason, we repeated the simulation study in Table 1(B), but with a misspecified diagnostic accuracy (γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.1 in (7)) for the imperfect reference standard. The resulting posterior disease probabilities given t_i = 0, 1, 2, 3, 4 were 0.02, 0.46, 0.70, 0.86, and 1.00, respectively. Table 1(C) shows that even with the misspecified diagnostic accuracy of the imperfect reference standard, the estimates of sensitivity and specificity are still nearly unbiased. Further, we are still able to distinguish between the true and misspecified models by using model selection criterion IC_H(0),Q: the percentages IC_H(0),Q selected the true random effects structure are around 90%.

Although the robustness of the proposed latent class model in estimating diagnostic accuracy is shown in Table 1 with the imperfect reference standard, we also investigate the sensitivity of the proposed model to different values of the diagnostic accuracy of the imperfect reference standard. Specifically, we estimate sensitivity, specificity, and prevalence for various values of the diagnostic accuracy of the imperfect reference standard by varying γ₂ in the parameterization given in (7). The simulations were also conducted with 500 replications for 100 individuals (I = 100). Table 2 shows results of the average estimated sensitivity and specificity in the population with five (J = 5) or ten (J = 10) raters under the scenarios that the true imperfect reference standard was generated from (7) with γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.2 and the misspecified imperfect reference standards with γ₀ = −4.5, γ₁ = 0.1, but γ₂ = −0.1, 0, 0.1, 0.15, 0.25, and 0.3 were used. Severe departure was not considered here, because it is not likely for investigators to use imperfect reference standards that have unreasonable poor quality. The simulation datasets were generated from the latent class models with random effects that follow mixture normal distribution and were fit to the models with normal random effects, but with the aid of the imperfect reference standard with an incorrectly specified diagnostic accuracy. As shown in Table 2, the robustness of the latent class model remains in all scenarios when the diagnostic accuracy of the imperfect reference standard is misspecified. Thus, the simulations demonstrate that exploiting the ordinal imperfect reference standard (e.g., a group of expert raters) and performing a sensitivity analysis provides a more robust solution than latent class models without a gold or imperfect reference standard for estimating diagnostic accuracy. Further, it is simpler to distinguish between competing models for the dependence between the experimental raters (e.g. ROB/GYNs) when we exploit the ordinal imperfect reference standard.

Table 2.

Simulation results for sensitivity and specificity with incorrectly specified imperfect reference standards. The random effects of the true models and working models always follow mixture normal distribution and normal distribution, respectively. The diagnostic accuracy of the imperfect reference was generated from (7) using different values of γ₂’s with _D and the diagnostic γ₀ = −4.5, γ₁ = 0.1. The corresponding posterior disease status $S_{1\mid t_i}^D$ accuracy parameter estimates are presented. The true imperfect reference standard was generated from equations (8) and (7) with γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.2. The true sensitivity, specificity and disease prevalence were set to be S_e = 0.90, S_p = 0.90, and π₁ = 0.7, respectively.

Number of tests	γ2	Posterior density ω1					Ŝe(se)	Ŝp(se)	π̂1(se)
		$S_{1\mid 0}^D$	$S_{1\mid 1}^D$	$S_{1\mid 2}^D$	$S_{1\mid 3}^D$	$S_{1\mid 4}^D$
5	0	0.02	0.65	0.70	0.74	1.00	0.90(0.065)	0.90(0.067)	0.69(0.050)
	0.1	0.02	0.46	0.70	0.86	1.00	0.90(0.071)	0.90(0.066)	0.71(0.048)
	0.15	0.02	0.36	0.70	0.90	1.00	0.91(0.061)	0.92(0.069)	0.70(0.047)
	0.25	0.02	0.20	0.70	0.95	1.00	0.90(0.060)	0.90(0.058)	0.69(0.057)
	0.3	0.02	0.15	0.70	0.97	1.00	0.91(0.071)	0.91(0.064)	0.70(0.049)
10	0	0.02	0.65	0.70	0.74	1.00	0.89(0.061)	0.90(0.045)	0.70(0.050)
	0.1	0.02	0.46	0.70	0.86	1.00	0.90(0.051)	0.90(0.054)	0.71(0.041)
	0.15	0.02	0.36	0.70	0.90	1.00	0.90(0.059)	0.89(0.051)	0.70(0.037)
	0.25	0.02	0.20	0.70	0.95	1.00	0.89(0.056)	0.91(0.048)	0.70(0.057)
	0.3	0.02	0.15	0.70	0.97	1.00	0.90(0.056)	0.90(0.063)	0.71(0.052)

One alternative of using the IE ratings is to incorporate both R-OB/GYNs and IEs into the latent class approach and fit a conventional model without a gold standard. We show the inherent problem of this alternative approach by considering the following model that was modified from Equation (1):

$$P(Y_{ij}=1\mid D_i=d_i,b_i,c_j)=\mathrm{\Phi }\left({\beta }_{d_i}+{\alpha }_{d_i}{E}_j+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j\right),{\sigma }_{d_i},{\tau }_{d_i}>0.$$ (9)

Equation (9) is (1) with the addition of E_j as an indicator variable for IEs where both types of ratings are included in the latent class model. To investigate the performance of (9) in estimating the sensitivity and specificity of the R-OB/GYNs, we set α₁ = −α₀ = 0.5 so that the IEs have higher sensitivity and specificity than the R-OB/GYNs. The simulation study in Table 1(A) was repeated under (9). Table S.1 in Web Appendix C of the web-based supplementary materials shows the results from the simulation study. In summary, the estimates of sensitivity and specificity of the R-OB/GYNs are biased when the dependence structure is misspecified. Further, the results shows that it is difficult to distinguish between the different models with this approach. In conclusion, the lack of robustness and difficulty in choosing between models makes the latent class approach on both R-OB/GYNs and IEs less attractive for incorporating the imperfect reference standard (IEs) than the proposed approach with a sensitivity analysis.

4 Application: the Physician Reliability Study in the Diagnosis of Endometriosis

The proposed methodology is applied to data from the PRS in the diagnosis of endometriosis. In this study, eight R-OB/GYNs diagnosed 79 subjects for endometriosis based on digital images from laparoscopies. Our interest is to obtain average sensitivity and specificity of the R-OB/GYNs in the diagnosis of endometriosis.

We estimated the diagnostic accuracy of R-OB/GYNs using the proposed latent class model with crossed random effects, under two random effects distributions for the between-subject and between-rater variation: normal distribution and mixture normal distribution. Table 3 shows the overall estimates of prevalence, sensitivity, and specificity for the diagnosis of endometriosis, as well as the IC_H(0),Q values of the fitted models. Bootstrap standard errors based 500 replications are also presented under each model. When no imperfect reference standard information is incorporated (Table 3(A)), estimates of diagnostic accuracy are close across models with the different random effects structures. For example, the sensitivity is 0.96 under the normal random effects distribution and is 0.93 under the mixture normal random effects distribution. The IC_H(0),Q values are also close for the two random effects specifications, suggesting that it is difficult to distinguish between the two models.

Table 3.

The estimates (standard errorss) of sensitivity, specificity, and disease prevalence, and IC_H(0),Q values of the models for the example of endometriosis diagnosis: (A) no gold or imperfect reference standard, (B) with an imperfect reference standard with the diagnostic accuracy specified by (7) with γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.2 (the resulting posterior disease probabilities given T_i = 0, 1, 2, 3, 4 were 0.02, 0.46, 0.70, 0.86, and 1.00, respectively). The random effects of the fitted models follow either normal or mixture normal distribution.

	Distribution of Random Effects	Estimated Sensitivity	Estimated Specificity	Estimated Prevalence	ICH(0),Q value
(A)
	Normal	0.96(0.079)	0.77(0.072)	0.69(0.024)	932.945
	MixN	0.93(0.084)	0.76(0.074)	0.69(0.025)	933.788
(B)
	Normal	0.93(0.074)	0.77(0.067)	0.70(0.027)	917.923
	MixN	0.93(0.086)	0.76(0.071)	0.69(0.031)	893.024

Due to the lack of a gold standard diagnosing endometriosis in the PRS, the ratings from the four IEs are used to construct an imperfect reference standard as stated in Section 2.2. This imperfect reference standard is ordinal, with T_i = 0 representing all four IEs’ diagnosing no disease for the ith subject and T_i = 4 representing all four IEs diagnosing the ith subject having endometriosis. Since the diagnostic accuracy of the imperfect reference standard is unknown, we first assumed that the diagnostic accuracy of the IEs was governed by setting γ₀ = −4.5, γ₁ = 0.1, and γ₂ = 0.2 in (7). The resulting posterior disease probabilities given t_i = 0, 1, 2, 3, 4 are 0.02, 0.46, 0.70, 0.86, and 1.00, respectively. The estimation results are reported in Table 3(B). Consistent with the simulation studies, the estimates of sensitivity and specificity from the models with normal and mixture normal random effects structures are very close. The model selection criterion IC_H(0),Q can distinguish the models and identifies the mixture normal model as the better model.

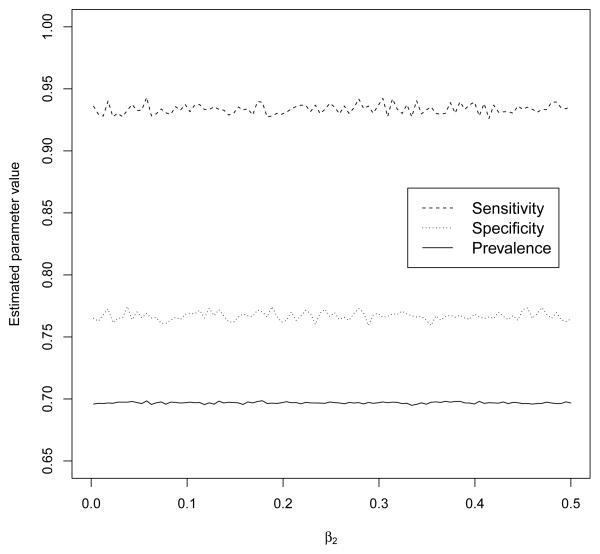
We further examined the robustness of the estimates of the proposed latent class model with respect to the different diagnostic accuracy of the imperfect reference standard information using (7). Figure 2 shows estimates of sensitivity and specificity, along with disease prevalence, for the latent class model that has normal random effects and incorporates the different imperfect reference standard information. The diagnostic accuracy of the imperfect reference standard was generated from (7) with γ₀ = −4.5, γ₁ = 0.1 and γ₂ changing from 0 to 0.5 by 0.01. Varying values of γ₂ corresponds to the probabilities $S_{1\mid t_i}^D$ as shown in Figure 1. The overall estimates of sensitivity and specificity for the R-OB/GYN physicians are nearly identical across γ₂. Thus, estimation of the average sensitivity and specificity forthe R-OB/GYNs are insensitive over a wide range of scientifically reasonable values of the diagnostic accuracy of the imperfect reference standard (derived from the IEs’ diagnoses).

Figure 2.

The results for the sensitivity study of the estimates of sensitivity, specificity, and disease prevalence to the change of the diagnostic accuracy of the imperfect reference standard in the PRS study of endometriosis diagnosis. A series of imperfect reference standards with different diagnostic accuracy was generated from (7) with γ₀ = −4.5, γ₁ = 0.1, and γ₂ change from 0 to 0.5 by 0.01.

5 Discussion

Estimating diagnostic accuracy without a gold standard is a challenging problem that has received substantial recent attention. Most of these methods involve latent class models where the true disease state is considered latent. However, these approaches have received criticism from a conceptual (Pepe and Janes, 2007) and robustness (Albert and Dodd, 2004) prospective.

In practical situations, we are still left with the problem of whether it is possible to estimate diagnostic accuracy when there is no gold standard. This was the motivation in the PRS where an important goal was estimating the sensitivity and specificity of diagnosing endometriosis from viewing intra-uterus digital pictures taken during laparoscopic surgeries for the R-OB/GYNs at a Utah site. Fortunately, we have additional information on a set of four IEs which we can exploit to estimate diagnostic accuracy of endometriosis among typical obstetrics and gynecology physicians. The methodology assumes that we know the diagnostic accuracy of the IEs, and we perform sensitivity analysis by varying this diagnostic accuracy in scientifically sensible ways. For this application, we are confident that when all raters agree there is only a negligible probability of misclassification. Hence, we primarily focus on varying the diagnostic accuracy for situations where the IEs differ. Through simulations and data analysis we show that the diagnostic accuracy estimation is remarkably robust to reasonable misspecification of assumed diagnostic accuracy of the IEs as well as to the distributional assumptions on the random effects for modeling the dependence among ROB/GYNs.

The robustness for estimating the diagnostic accuracy of the R-OB/GYNs to the assumed accuracy for the IEs is in part due to the low frequency of discordance in IEs’ ratings, and the reasonable assumption that there is no misclassification when all IEs agree. We expect that estimation will be more sensitive to variation in the diagnostic accuracy of the imperfect standard when there is less consensus among the IEs. Our approach will still be useful in this case since we can report ranges of diagnostic accuracy estimates of R-OB/GYNs corresponding to ranges in the assumed diagnostic accuracy of the IEs.

This work has important implications for diagnostic accuracy studies, suggesting that exploiting expert raters or multiple high quality tests may provide a good approach for estimating diagnostic accuracy of other raters or tests. Especially, we showed that these types of experts raters or high quality tests can greatly improve the robustness of the estimation with respect to the misspecification of random effect distributions in the latent class models. Thus, this approach provides a robust alternative to traditional latent class models for estimating diagnostic accuracy without a gold standard.

The use of IE data is one of the key aspects in the application of the proposed methodology. First, the fact that the inference are not sensitive to parameters of the polychotomous logit model is in part due to $S_{1\mid 4}^D\approx 1$ and $S_{0\mid 0}^D\approx 1$ for all parameters considered. This is sensible since it would seem very unlikely that one would have a positive (negative) gold standard when all the IEs were negative (positive). One would need a large enough group of IEs to have this confidence, with this number being application dependent. However, for a general rule, we recommend a minimum of four expert ratings. Second, we conducted simulation studies to investigate the performance of the proposed method when IEs only examine a subset of the patients. Estimates of the sensitivity and specificity of the R-OB/GYNs are nearly unbiased under a misspecified dependence structure when the IEs examine 80% and 50% of the patients. When the proportion of examined patients decreased to 20%, the estimates have substantially more bias. Third, we conducted simulation studies to investigate the performance of the proposed method when the patients are not examined by all IEs. The simulations indicate that the estimates of the sensitivity and specificity of the R-OB/GYNs are robust to dependence misspecification. Therefore, we suggest that, when the patients are not examined by all IEs, the proposed method can still function very well with the appropriate imputation for the missingness. Please see Web Appendix D in the web-based supplementary materials for simulation results.

The use of the proposed polychotomous logit model for the imperfect reference standard provides nearly unbiased estimation of the diagnostic accuracy and disease prevalence, regardless of whether or not the IEs are exchangeable (exhangeablilty of the four IEs means, for any combination of e₁, e₂, e₃, and e₄, $P({\stackrel{\sim }{T}}_i^{(1)}=e_1,{\stackrel{\sim }{T}}_i^{(2)}=e_2,{\stackrel{\sim }{T}}_i^{(3)}=e_3,{\stackrel{\sim }{T}}_i^{(4)}=e_4\mid D_i=d_i)=P(T_i={\sum }_{l=1}^4{e}_l\mid D_i=d_i)$, where d_i = 0 or 1). Also, in (5), we assume independence between the random effect b_i and the imperfect reference standard T_i. In the circumstance where these assumptions are violated, the proposed methodology is still able to provide robust estimates for the diagnostic accuracy of R-OB/GYNs and disease prevalence (please refer to Web Appendices E and F in the web-based supplementary materials for more detailed discussions of these two points).

The focus of this work was on estimating diagnostic accuracy measures such as sensitivity, specificity, and prevalence. Other work in the area of diagnostic testing have criticized these measures in favor of positive and negative predictive value (Moons et al., 1997). These alternative measures can easily be estimated from estimated sensitivity, specificity, and prevalence discussed in this paper. The analysis of the PRS data with the new methodology show that the average R-OB/GYN’s sensitivity is high (≈0.93) with the average specificity being rather low (≈0.77). This is important new information since it suggests that R-OB/GYNs are overly diagnosing endometriosis in regular clinical practice.