Stress distribution on a three-unit implant-supported zirconia framework. A 3D finite element analysis and fatigue test

SUMMARY

Purpose

The purpose of this study was to investigate, by finite element analysis (FEA) and fatigue analysis, the influence of different loading conditions on the stress distribution in a 3-unit implant-supported Y-TZP fixed partial denture (FPD).

Material and methods

A three-dimensional FEM model was developed. The materials used in this study were assumed to be linearly elastic, homogeneous and isotropic. 100 N and 300 N loads over a 0,5 mm² areas with different angles (0°, 15° and 35°) and locations were applied on the prosthesis and the distribution of equivalent von Mises stress was investigated. A fatigue analysis was carried out too.

Results

Maximum stresses were found at the connector region of the framework when the intermediate element is loaded (100 N load pattern: 32,9 MPa, 33 MPa and 51,8 MPa; 300 N load pattern: 98,6 MPa, 102,8 MPa and 155,7 MPa, respectively with 0°, 15° and 35° of inclination). Results confirmed the vulnerability of both connector areas even if just one pillar was loaded with an increase in stress when angle of load inclination is larger. The cyclic fatigue evaluation indicates a strong propensity for fatigue behavior, presenting a considerable range of loading conditions. No fracture fatigue occurred with a 100 N force. A 300 N force applied to the pontic produces no fatigue problems because the load is equally shared by whole system. A 300 N force applied to one of the two pillars, or to both implants generates fatigue problems.

Conclusion

F.E.M. analysis of a 3-unit implant-supported Y-TZPFPD, give accurate information about loading conditions for clinical success over time. Fatigue analysis results show structural reliability of the Y-TZP as framework material for 3-unit posterior FPDs.

Introduction

Success of implant rehabilitation depends on factors concerning biological, biomechanical as well as clinical practice. Failure may result from loss of osseointegration or component failure subsequent to restoration and may be related to unfavorable loading or to high stress concentrations (1,2).

Implant superstructures material and design affect load transfer and physiological turn over of bone cells. In recent years, there has been increasing interest in the replacement of missing teeth using fixed partial dentures (FPDs) with oxide-ceramic frameworks (3,4).

All-ceramic restorations are used as an alternative to metal-ceramic restorations (PFM) and are becoming more popular because of material improvements and advances in fabrication technologies. Thanks to CAD/CAM technology, high-strength ceramic materials can be milled with accuracy, standardized manufacturing processes and reduced production costs (5,6).

The most recent core material for all-ceramic FPDs is yttrium-oxide partially-stabilized (Y-TZP) zirconia. This oxide ceramic was introduced for biomedical use in orthopedics for total hip replacement and was highly successful because of the material’s excellent mechanical properties and biocompatibility (7).

Y-TZP demonstrates better mechanical performance, superior strength and high fracture resistance compared with other all-ceramic cores. Oxide ceramic exhibits many desirable properties, including high biocompatibility with reduced bacterial surface adhesion, low thermal conductivity, abrasion resistance, color stability and aesthetics (8).

Major drawbacks of all-ceramic restorations, not supported by Y-TZP coping, are brittleness, relatively low flexural and tensile strengths, which limit their use as framework of posterior fixed partial dentures (FPDs) (9–13). Y-TZP has a flexural strength of over 1000 MPa (14–16), a fracture toughness up to 10 MPa/m^0.5 and a modulus of elasticity value of 210 GPa (17–19) which makes it possible to offer an all-ceramic bridge even in the posterior region, where high demands of strength are required. Most of failures, in vitro and in vivo, occurred due to fracture of the connector area, which is a locus minoris resistentiae (11, 20–23).

However the failure of a restoration may be the result either of framework fracture or chipping of veneering material. Both events might cause functional and aesthetic problems for the patient leading to the need to remove the prosthetic device. YTZP is especially suited from situation with high demands of strength, but a biomechanical design of the framework is mandatory. During chewing function, bending forces lead to tension at the gingival side of the connector area, thus promoting cracks and subsequent fracture. Studies using finite-element analysis demonstrated that during occlusal loading the highest stress within FPDs was located at the gingival side of the connector area (24, 25). Oh et al. (26, 27) demonstrated in a finite element analysis and in an in vitro study that connector fracture was initiated at the gingival embrasure and that a larger radius of curvature at the gingival embrasure reduces the concentration tensile stresses, thus affecting the fracture resistance of the FPD.

The purpose of this study was to investigate, by means of finite element analysis, the effect of various force modules, simulating the functional occlusal contact, on stress distribution through a 3-unit implant-supported Y-TZP FPD.

Materials and methods

Three dimensional FEA model reproducing a 3-unit FPD, was constructed in order to evaluate stress levels in the single components of the system under several loading conditions. The geometry of the restoration simulated one of the most common prosthetic option in the daily practice, an implant-supported bridge between two fixtures placed in the first premolar and in the first molar regions.

The model was created in 3D using the solid modelling software (Solidworks office 2007, Solid-works Corporation).

The framework was developed according to manifacturer’s instruction and guidelines on Y-TZP coping (values according to in-house testing, Nobel-Procera, NobelBiocare AB, Goteborg, Sweden). The design of the framework respect the anatomical form of the final restoration allowing an occlusal veneering thickness of minimum 1 mm - maximum 2 mm. The framework design had round edges and anatomically customized with a minimum thickness of 0.6 mm. The connector dimension of a multiple unit framework depends on the distance between the supporting pillars. The minimum connector area for a three-unit bridge supported by two implants placed in the posterior area, up to 20 mm away from each other, is 9.4 mm² (height x width = 4.0 × 2.5). The design of the core involving aproximal contact areas assures an appropriate support of marginal ridge allowing a veneering strength of 0.7 – 1.5 mm.

The geometry for the implant and abutment designs was obtained from 2D drawings of components provided by the implant manufacturer (BT-Lock srl, Vicenza, Italy).

Two titanium fixtures 4.50 × 13-mm were selected for this study. The abutments used had a diameter of 4.70, a total length of 5.90 mm, a total axial taper of 6 degrees and a 1 mm depth radial slight chamfer shoulder. This marginal design demonstrated to be the configuration that transmits less stress concentration (28).

The 3D model abutment screw, fixed the abutment to the fixture with a 25 Ncm torque.

The framework was developed according to manifacturer’s instruction and guidelines on Y-TZP coping (values according to in-house testing, NobelProcera, NobelBiocare AB, Goteborg, Sweden). The design of the framework respect the anatomical form of the final restoration allowing an occlusal veneering thickness of minimum 1 mm - maximum 2 mm. The framework design had round edges and anatomically customized with a minimum thickness of 0.6 mm. The connector dimension of a multiple unit framework depends on the distance between the supporting pillars. The minimum connector area for a three-unit bridge supported by two implants placed in the posterior area, up to 20 mm away from each other, is 9.4 mm² (height x width = 4.0 × 2.5). The design of the core involving aproximal contact areas assures an appropriate support of marginal ridge allowing a veneering strength of 0.7 – 1.5 mm.

The restoration was luted to the abutments with a 0,025 mm thickness dual cured resin cement (RelyX ARC, 3M ESPE AG, Seefeld, Germany).

The physiologic conditions could have been approximated by simulating the mandibular body, but the aim of the study was to evaluate only the biomechanical reliability of the prosthetic device. Thus bone volume was not considered and a smaller model was proposed.

The model was imported for finite element analysis in the FEM calculation software ANSYS 7 (ANSYS Inc., Canonsburg, Pennsylvania, USA).

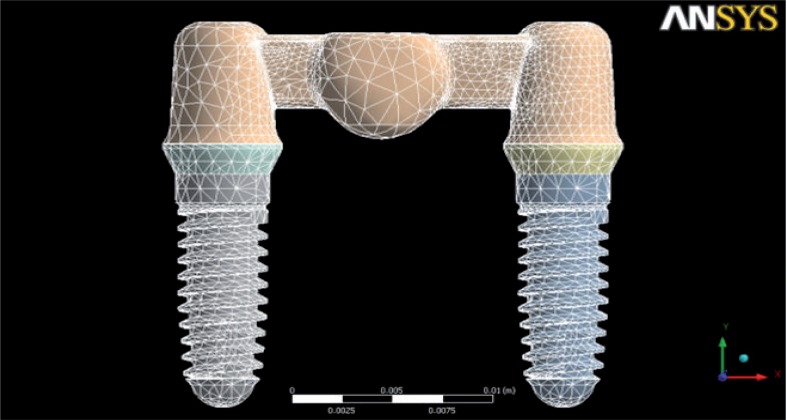
The mesh was developed by SOLID187 elements, three-dimensional elements formed by 10 knots and very suitable for developing mesh on irregular bodies. It was achieved by a stress convergence analysis (through successive refinements with a σ_max change to more than 10%) and it was divided in 224.620 elements connected at 375.629 points known as nodes (Fig. 1). The displacement of each of the nodes had to be calculated to determine the stress throughout the structure.

Figure 1.

Three-dimensional finite element Y-TZP FPD model mesh.

A finer mesh was generated at the material interface to ensure accuracy of force transfer. All materials used were assumed to be linearly elastic, homogeneous and isotropic. The mechanical properties were data supplied by the manufacturers and are showed in Table 1.

Table 1.

Mechanical Properties of Prosthetic Materials in Finite Element Analysis Evaluations.

Material	E [MPa]	G [MPa]	v	Fatigue [MPa] R=−1	Manifacturer
Y-TZP	210000	80769	0,33	550 n° of Cycles 1.00e+6	NobelProcera, NobelBiocare AB
Cement	5100	2008	0,27		RelyX ARC, 3M espe AG

The model simulated an ideal osseointegration, so the fixtures were rigidly anchored along their entire interfaces. A fixed constraint on the external thread was applied, while non-threaded portion was bound only in the xz directions to allow tangential movement as well as happens in a clinical situation. A static-structural analysis was performed to study the linear elastic materials behaviour. Three loads from different directions (0°, 15° and 35°) were selected. Axial and oblique loads of 100 N and 300 N were applied equally to the nodal points on the buccal side over a 0,5 mm² area on the stamp cusps.

Four different loading conditions were applied: loading of all teeth to simulate maximum centric occlusion contacts, loading of the single element of the framework to simulate single posterior contact. Stress distribution within the elements was expressed in terms of von Mises equivalent stress and was compared with the yield strength values (29, 30). Von Mises stress values were used to compare the stress distribution in ductile materials, whereas normal principle stress values were evaluated in determining the resulting stress types. Calculated numeric data were transformed into color graphics to better visualize the mechanical phenomena in the models. Determined that maximum von Mises equivalent stress, seen as failure criterion, calculated on all elements, was lower than the yield strength value of the material, a further analysis was carried out. In particular the maximum value was used as reference value for the following fatigue analysis.

Results

Analysis performed showed that the material behavior is linearly elastic until the fracture. Von Mises stress equivalent was used as yield strength criteria in the following pages.

The analysis of the von Mises stress values revealed that maximum stress concentration were located at the loading areas. High stresses always occurred throughout the marginal region of the prosthesis. Lower stresses were associated with the occlusal regions of the prosthesis, where the loading originated. Therefore stresses increased from the occlusal level toward the gengival area. The highest stress values were located at connectors and cervical regions of abutments. Occlusal and gingival embrasures of connectors were the areas of more intensive stress concentrations with the higher stress observed at cervical embrasure of the connector, between pontic and abutment.

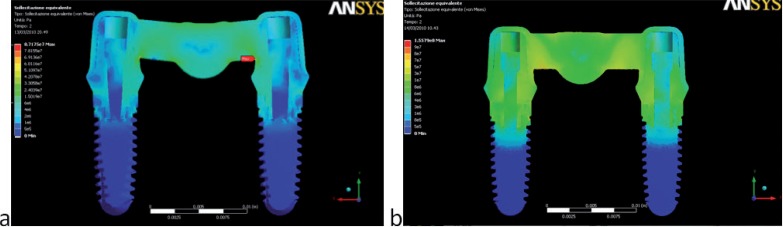
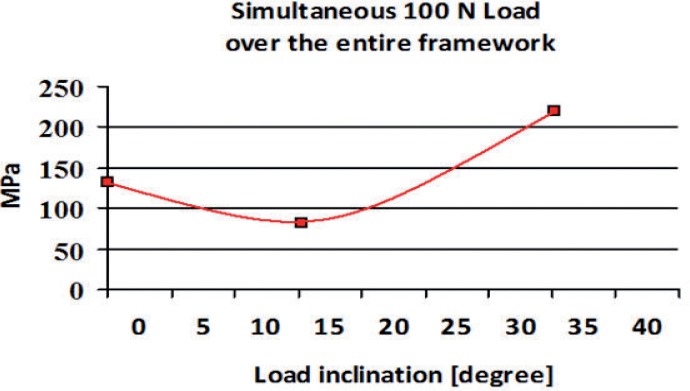
Two different behaviors were observed in the stress distribution when the load was applied to the pontic element or to the pillars. The maximum stress was located at the connector regions of the bridge because it bended when the pontic element was loaded (Fig. 2). In the other two cases the maximum stress was found on the abutment of the pillar loaded (Figs. 3,4). Tensions rose with increasing inclination of the load (Figs. 5, 6).

Figure 2.

von Mises stress values (Pa) and distributions found when the pontic load was applied: (a) 100 N – 0°; (b) 300 N – 35°.

Figure 3.

von Mises stress (Pa) values and distributions found when the abutment load was applied (posterior loading): (a) 300 N – 0°; (b) 300 N – 35°. High stress rises in both connector regions also when the load is applied on one pillar abutment.

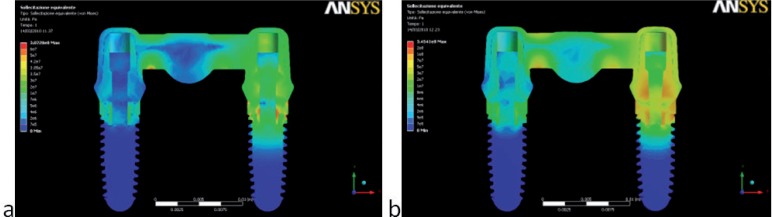
Figure 4.

von Mises stress values (Pa) and distributions found in the physiological load: (a) 100 N – 0°; (b) 100 N – 15°. Connector regions show maximum stresses.

Figure 5.

Distribution of von Mises Stress (MPa) under 300 N load on single element of the framework.

Figure 6.

Distribution of von Mises Stress (MPa) under simultaneous 100 N load over the entire framework.

Y-TZP physical data were obtained from literature (31–34). Y-TZP shows very high static and cyclic fatigue strenght due to its polycrystalline structure. Following values were obtained from tests carried out on Y-TZP samples (35–37):

• σ_R 1000 MPa (fracture tension)

• σ_a^∞ 550 MPa considering a number of cycles of 2 × 10^a6

where σ_a^∞ is the fatigue strength limit and (R= −1) is the ratio cycles (2 × 10⁶)

From these data exact value σ_a^∞,−1 can be found using the following formula:

$${\sigma }_{a^{\infty },-1}^{*}=\frac{{\sigma }_{a^{\infty }}\left(R=-1\right)}{K_f{K}_d{K}_l{K}_v}=\frac{550}{1\cdot 1\cdot 1.15\cdot 1}=478,3MPa$$

where K’s are factors which influence Y-TZP fatigue life (K_f shape, K_d size, K_l surface finishing, K_v stress type).

Since chewing function is constituted by alternating loading cycles and different loadind patterns, whose values vary from minimum stress (σ_min =0), to maximum stress (σ_max), σ_a^∞ (R= −1) obtained from experimental data, must be converterd into σ_a^∞ (R= 0) and the previous formula into:

$${\sigma }_{a^{\infty },0}^{*}=\frac{{\sigma }_R\cdot {\sigma }_{a^{\infty },-1}^{*}}{{\sigma }_R+{\sigma }_{a^{\infty },-1}^{*}}=\frac{1000\cdot 478,3}{1000+478,3}=323,5MPa$$

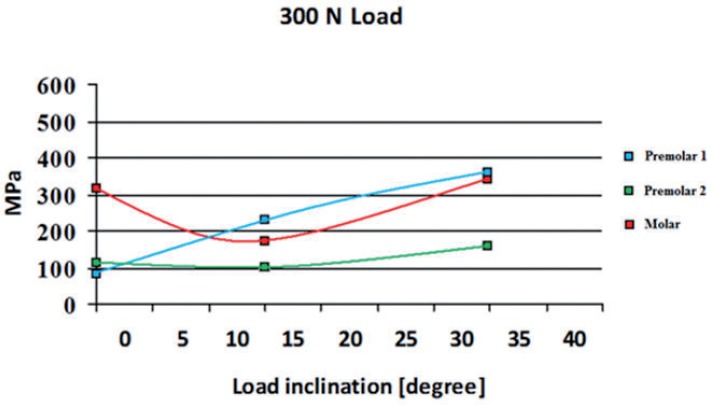
Maximum tension values obtained from numerical analysis with different intensities (100N and 300N) and angles (0°, 15° and 35°) can be used for Y-TZP fatigue analysis. As Table 2 showed, no fracture fatigue occurred with a 100 N force, because σ_α < σ_α^∞,0. Thus, no framework fracture occurred after an infinite cycle number. Applying a 300 N force to the pontic no fatigue problems occurred because the load is equally supported by whole system. A 300 N force applied to one of the two pillars, or to both implants generates fatigue fracture (Tab. 2).

Table 2.

Maximum stress and fatigue strength values obtained in the simulations. Red values indicate prosthesis maximum stress (σ_max) and fatigue strength limit (σ_a^∞,0) determined by chewing function alternating cyclic loading.

	Angle	Max Tension (F=100N)	Max Tension (F=300N)	σa,max	σa∞,0
PREMOLAR1	0	27,3	81,8	40,9	166,8
	15	70,8	212,5	106,25	166,8
	35	121,1	363,2	181,6	166,8
PREMOLAR2	0	32,9	98,6	49,3	323,5
	15	33	102,8	51,4	323,5
	35	51,8	155,7	77,85	323,5
MOLAR	0	102,4	307,3	153,65	166,8
	15	44,2	174,7	87,35	166,8
	35	115,1	345,4	172,7	166,8

Discussion

The FEM has been shown to be a useful tool when investigating complex systems that are difficult to standardize during in vitro and in vivo investigations (38).

In this study, the finite element stress analysis technique was used to compare stress distribution on the Y-TZP frameworks of 3-unit implant-supported fixed partial dentures in the lower jaw. Different types of loading were applied to the framework. The validity of finite element stress analysis results depends on the precision with which the geometry, material properties, interface condition, support and loading are in accordance with physical reality.

The materials were all assumed to be homogenous, isotropic and to possess linear elasticity. Thus, the inherent limitations in this study should be considered.

When applying FEA to prosthesis, it is important to take in consideration not only axial loads but horizontal (moment-causing loads) and combined forces (oblique occlusal force) too. This stress pattern is very close to physiological occlusal loading and will result in localized stress at cervical area and at the implant neck. The nodal points of load application were on the buccal side of the framework with an occlusal force of 100 N and 300 N.

The stress values are lower than the material strength of the applied materials.

The results showed that maximum stress value trend was the same for the two loading conditions applied (100 N and 300 N), because constraints and geometry were the same for the two analyses. The structure response was the same, while maximum stress values varied. Tension values increased when the angles of oblique load became larger (35°), probably due to a flexural component that accentuated the stress peak on the implant.

An exception could be found when the load was applied to the pontic of the bridge.

The simultaneous 300 N loads applied on the molar (under the two stamp cusps) was the most critical situation obtained in the simulations. High stress always occurred throughout the marginal area of the prosthesis. Stress increased from the occlusal level toward the marginal area. Slight chamfer could be the best geometry to minimize the stress. Smooth and round framework design is indicated to increase the resistance to fracture. Thus, a prosthesis, because continuously subjected to alternating loads due to chewing, has a greater long term performance with more extensive connections. Prostheses supported by 1 or 2 implants replacing missing posterior teeth are subjected to an increased risk of bending overload (39). The type of loading may influence the stress patterns developed. Research has shown that the connector is the weakest region of an FPD (40–47) even if most of this researches applied load just at the center of the pontic (40, 41, 48). In the physiological pattern load is distributed to the entire surface of the restoration involving all the main parts: pillars and pontic (49). The weakness of connector area and its fracture strength to the fatigue stress depends on connector length, width and height. The functional and aesthetic customized design of the framework oblige to different sizes of the two connectors, with premolar’s one shorter. Higher stress values resulted in the longer connector molar region. Therefore it is mandatory to increase width and height in proportion with the increasing length. In the current study, load was applied over the entire framework surface in correspondence of the two pillars and the pontic element. Results confirmed the vulnerability of both connector areas even if just one pillar was loaded. The high elastic modulus of YTZP, used in the present study, ensures a uniform distribution of biomechanical stress within the framework, providing more efficient load transfer and long term predictability of the restoration. The primary cyclic fatigue evaluation indicates a strong propensity for fatigue behavior, presenting a considerable range of loading conditions, where cyclic fatigue can be detected.

Conclusion

Within the limitation of FEM three dimensional analysis, the following conclusions may be drawn: maximum von Mises stress values were concentrated around the gengival area of the Y-TZP frameworks, in the connector regions and in the cervical regions of abutment; the connector regions presented the highest tensile stress values with risk of fracture; there is a significant change on the stress distribution and on the tensile stress values when the loading condition is changed. Tension values increased when the angles of oblique load became larger (35°). Fatigue tests give accurate information about reliability of YTZPas framework material in 3-unit posterior region FPD. Further tests must be performed to simulate the real clinic condition and to ensure that the FEM results are transferable to clinical situations.