Highly Efficient Light-Trapping Structure Design Inspired By Natural Evolution

Abstract

Recent advances in nanophotonic light trapping open up the new gateway to enhance the absorption of solar energy beyond the so called Yablonovitch Limit. It addresses the urgent needs in developing low cost thin-film solar photovoltaic technologies. However, current design strategy mainly relies on the parametric approach that is subject to the predefined topological design concepts based on physical intuition. Incapable of dealing with the topological variation severely constrains the design of optimal light trapping structure. Inspired by natural evolution process, here we report a design framework driven by topology optimization based on genetic algorithms to achieve a highly efficient light trapping structure. It has been demonstrated that the optimal light trapping structures obtained in this study exhibit more than 3-fold increase over the Yablonovitch Limit with the broadband absorption efficiency of 48.1%, beyond the reach of intuitive designs.

Solar radiation provides an abundant supply of free energy in nature. Efficient utilization of solar energy could address the most urgent problem facing the industrialized world for its reliance on fossil fuels to generate electricity. Light trapping was therefore developed to extend the path-length for light interacting with the active layer, so high-efficiency thin film solar cell can be created using much less active materials with the benefit of cost reduction. However, as the active layer becomes notably thinner than the wavelength of the light, the statistic ray-optics approximation used to derive the Yablonovitch Limit¹ no longer holds²,³,⁴. Instead, the evanescent wave can contribute to substantially enhance the absorption of the solar energy, resulting in the improved performance beyond such a classical limit⁵,⁶. As an example, Yu et al. reported a maximum absorption enhancement factor of 12×4n² at a single wavelength by designing a nanostructured dielectric grating that couples the incident light to a 5 nm thick slot waveguide modes using weak absorbing active medium⁵. Similarly, a wide range of periodic light trapping structures have been reported, such as triangular or pyramid grating⁷,⁸, nanoparticles⁹, nanowires⁴, nanoholes¹⁰, nanocones¹¹, photonic crystals¹²,¹³, and plasmonic nanostructures¹⁴,¹⁵,¹⁶,¹⁷. Pursuing the optimal light trapping techniques requires a careful consideration of the competing physical processes, including light refraction, deflection, and absorption. However, these works are conducted in an ad-hoc fashion that relies on physical intuition to predefine the topology of the light-trapping structure and thus, not capable of handling the topological variation in reaching the optimal design. Therefore, it calls for a general, yet systematic methodology that is capable of seeking the optimal topology in delivering highly efficient light trapping designs beyond intuition.

While facing challenges in designing effective topology for functionalities, through billions of years of evolution, nature often presents its unique but surprisingly elegant solutions that far excel the modern engineering designs¹⁸,¹⁹. For instance, the nature-created topology in moths compound eyes, which consists of a hexagonal arrays of nipples, act as an anti-reflection coating (ARC) with gradual refractive index profile²⁰,²¹,²²; diatoms have the unique hierarchical periodic structures in the frustule to diffract incoming light for efficient energy harvesting²³, long before the concept of photonic crystals (PhCs) was ever conceived. Inspired by the natural evolution process, we report a new methodology for designing nanophotonic light trapping structures by adopting the topology optimization approach for problem formulation and the genetic algorithm as the search algorithm. Topology optimization was originally developed for solving mechanical structure design problems²⁴,²⁵,²⁶. The underlying idea of conventional topology optimization is to recast a structural design problem as a material distribution optimization problem such that an optimized geometric configuration fulfills a prescribed set of performance targets. Within the last decade, this approach has been successfully extended to various photonic design problems²⁷, such as 2D photonic crystal band-gap maximization²⁸,²⁹,³⁰, low-loss photonic waveguide design³¹, design of photonic structure for light confinement³² and invisibility cloak optimization³³. Innovative and optimal structures are obtained for these problems by using topology optimization methods. Nevertheless for the complex light-trapping problem in thin-film cells, limited work has been conducted utilizing topology optimization to achieve efficient designs.

Results

Methodology and test model of thin film solar cell

Topology optimization methods can be generally categorized into two classes based on whether gradient information is used in searching the optimal solution, i.e. gradient-based topology optimization (GTO) methods³⁴,³⁵,³⁶ and nongradient-based topology optimization (NGTO) methods³⁷,³⁸,³⁹. The complexity of solution space in light-trapping structure design problems impairs the guidance provided by local gradients for global optimum, i.e., solutions from GTO are often trapped at local optimum of inferior performance. Under this circumstance, NGTO is more competent in searching for high performance designs by using the global search techniques. Genetic algorithm (GA) based NGTO is used in this work to optimize the geometry (topology) of the optical scattering layer to achieve highly efficient light-trapping structures. Mimicking the natural evolution with the underlying idea of survival-of-the-fittest, GA is a stochastic global search approach⁴⁰,⁴¹ that involves iterative operations of selection, recombination (crossover) and mutation on a population of designs. Owing to their competency for highly nonlinear problems and convenience for parallel computing, GAs have been widely applied in photonics design²⁸,³²,⁴²,⁴³. For design evaluations, the Rigorous Coupled Wave Analysis (RCWA) method⁴⁴,⁴⁵, which is efficient in evaluating diffraction efficiencies of optical gratings and multilayer stacks¹³, is adopted in this work to numerically calculate the absorption in the active layer. In RCWA, Fourier expansions of both the field and the permittivity lead to an algebraic eigenvalue system for each layer, one of which is the light scattering layer⁴⁴. The electromagnetic fields in each layer are determined by solving the eigenvalue problems. The boundary conditions are then applied in sequence at the interfaces to yield the reflected, transmitted and diffracted field amplitudes⁴⁵. Therefore, the absorption of each design can be calculated by the law of energy conservation.

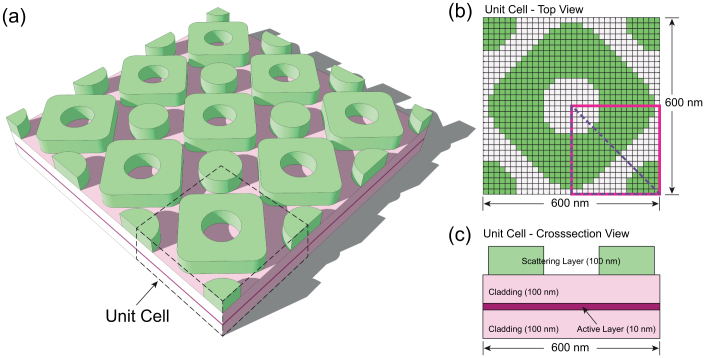
As shown in Figure 1(a), the test structure of thin-film organic solar cells consists of a 10 nm thick P3HT:PCBM active layer that is sandwiched between two 100 nm thick cladding layers made of high index gallium phosphide (GaP), and a nano-structured light scattering layer on top⁵,⁶. The scattering layer couples the incident sunlight to the corresponding slot waveguide modes by matching the differences in wave vectors. The optical field will then be confined within the active layer by the virtue of the slot waveguide effect⁴⁶. In this process, the scattering layer plays a critical role in balancing the competing process of light reflection at the front interface due to the impedance mismatch and the light diffraction for effective coupling to the slot waveguide modes. For such a coupled physical process, it is difficult to find the optimal light scattering layer design through prior structural fixation based on intuition⁵,⁴⁷. To formulate this design problem as a dielectric material distribution optimization problem, the design space, i.e. one unit cell of the scattering layer, is discretized by a 32-by-32 finite element mesh shown in Figure 1(b). Design variables are material assignments in each discretized element, taking binary values of either 0 or 1 representing air or dielectric material, respectively. The unit cell size is selected to be 600 nm. The selection of the dielectric material is either a typical polymer with n = 1.7 or GaP with n = 3.57. The complex refractive index of the P3HT:PCBM active layer is set to be 1.9+0.156i in the optimization⁴⁸.

Figure 1. Light-trapping structure of the test case for optimization.

(a) The test structure consists of a 10 nm thick P3HT:PCBM active layer that is sandwiched between two 100 nm thick cladding layers made of high index material, and a nano-structured light scattering layer on top. The scattering layer has periodicity 600 nm. The material of the scattering layer is either air or a dielectric, which is GaP or polymer with refractive index 1.7, as two different test cases. (b) The unit cell of the real space scattering pattern discretized with 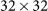meshes. Green corresponds to high-index dielectric material and white regions are air. (c) The cross-section view of the unit cell of the light trapping structure.

With the cell architecture shown in Fig. 1(c), the light scattering layer is optimized using GA based NGTO. Since the invention of GA method in 1975⁴⁰, a wild array of variants of the original GA have been developed. In this work the standard GA⁴¹ is used, which is a mature approach with proved satisfactory performance in solving relevant nanophotonic problems²⁸,²⁹,³². As shown in Eq. (1), the optimization objective is to maximize light absorption coefficient in the active layer:

where A is the absorption coefficient, R is the zeroth-order reflection, T is the zeroth-order transmission, D is deflection that consists higher order reflection and transmission and ε is the permittivity distribution to be optimized. No constraint on material consumption is applied owing to the fabrication flexibility.

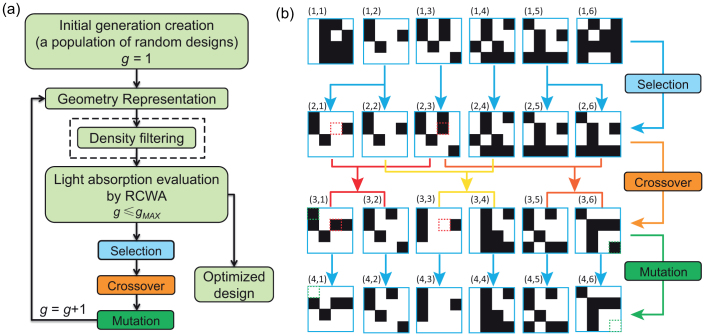
The optimization framework is shown in Fig. 2(a), while Fig. 2(b) schematically illustrates the operation principle of selection, crossover, and mutation in GA. For the purpose of demonstration, a population of 6 individual topological designs is assumed with each of these designs represented by the 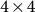elements (each element is known as a gene in GA). In this process, an initial generation containing a population of random designs is first created (as the numbered designs (1,1~6) in Fig. 2(b)) and their fitness values are determined by absorption coefficient evaluated using the RCWA method. After obtaining the absorption performance of each design in the population, promising individuals with higher fitness values are selected with better chance for reproduction. As shown in Fig. 2(b), designs (1,2), (1,3), (1,4), (1,5) are selected to form the mating pool, i.e. designs (2,1~6), following the idea of survival-of-the fittest, while designs (1,2) and (1,5) are selected twice respectively due to their superior performance. The selected designs then undergo recombination also known as crossover, involving a structured, yet randomized exchange of parental traits. In Fig. 2(b), three mating pairs are randomly picked from the mating pool, i.e. designs (2,1) and (2,3), designs (2,2) and (2,4), and designs (2,3) and (2,6), each of the pairs produces two offsprings, i.e. designs (3,1) and (3,2), designs (3,3) and (3,4) and designs (3,5) and (3,6), respectively. During crossover, genes of a mating pair at the same loci switch with each other stochastically, such as the highlighted gene loci in designs (2,1) and (2,3). After the crossover, genes in each design may mutate to their opposite phase at a very small probability for potential local refinements which is hard to achieve through crossover. As an illustration in Fig. 2(b), designs (4,1) and (4,6) are obtained from designs (3,1) and (3,6), respectively with mutations at the highlighted gene loci, while the rest designs remain the same. Absorption coefficient values of the new-born generation (designs (4,1~6) in Fig. 2(b)) are then re-evaluated. This optimization loop iterates until the final convergence when all designs within the population tend to be similar and their absorption performance are significantly improved. This stochastic search process mimicking the biological evolution is robust to the nonlinearity of this problem. For an optimization problem with a complex solution space, regularization techniques, such as filtering techniques (Fig. 2 (a)), are required to ensure the solution existence⁴⁹.

Figure 2. Genetic algorithm based topology optimization for light-trapping structure design.

(a) The flowchart of Genetic Algorithm (GA) based topology optimization. 2D scattering pattern is represented with bit-array and rigorous coupled wave analysis (RCWA) is adopted to evaluate the absorption coefficient for each design. Designs are then optimized based on the corresponding absorption coefficients using GA that consists of selection, crossover, and mutation. The density filtering technique is utilized to treat numerical instabilities. (b) Schematic illustration of a typical operation of selection, crossover, and mutation of GA within one evolving iteration. An initial generation of 6 individual designs (1,1~6) with 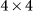elements is first created. Each element is known as a gene in GA. Designs (1,2), (1,3), (1,4), (1,5) with superior performance are selected to form the mating pool, i.e. designs (2,1~6). While designs (1,2) and (1,5) have been selected twice respectively due to their outstanding performance and keeping population constant. Then three mating pairs are randomly picked from the mating pool and each pair generates two offsprings, i.e. ((2,1), (2,3)) ((3,1), (3,2)), ((2,2), (2,4)) (3,3), (3,4)), ((2,3), (2,6)) ((3,5), (3,6)), respectively. During the crossover, genes of a mating pair at the same loci switch with each other stochastically, such as the highlighted gene loci in designs (2,1) and (2,3), and result in the highlighted gene loci in designs (3,1) and (3,2). After the crossover, genes in each design may mutate to their opposite phase at a certain probability. Designs (4,1) and (4,6) are obtained from designs (3,1) and (3,6) respectively with mutations at the highlighted gene loci, while the rest designs remain the same.

The 1^st test case for optimization at single wavelength

In the first optimization case, to simplify design problem associate with multiple governing factors, which often result in a complex solution space with numerous local optima, the low refractive index polymer material (n = 1.7) was used to construct the scattering layer. Under the effective medium approximation, the effective refractive index of the scattering layer is determined by averaging the dielectric and air regions⁵⁰, ranging from 1 to 1.7, which is much smaller than that of the cladding layer (3.75). Therefore, the reflection at the top surface due to the impedance mismatch becomes insensitive to the variation of the scattering layer while leaving the diffraction and the subsequent mode coupling being the dominating factors in the optimization process. This step allows us to validate the design methodology using the less complicated physical process.

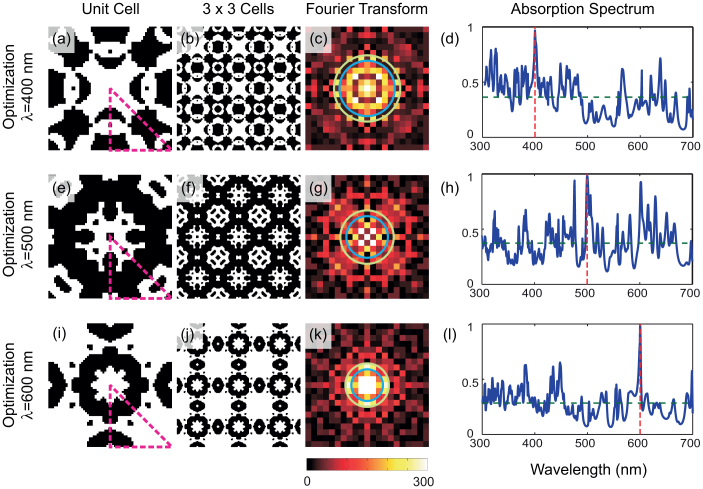
The D₂ symmetry is imposed upon the unit cell of scattering layer for reducing the computational cost of topology optimization. Optimization starts from the initial generation composed of random designs as shown in Fig. 3(a), (b). The scattering patterns that maximize the absorptions of 400 nm, 500 nm and 600 nm for normal incidence are shown in Fig. 3(d) and (e), (g) and (h), (j) and (k), respectively. Starting from a random structure, the optimization converges to periodic and symmetric structures, which illustrates the strength of topology optimization as a powerful structural optimization tool. The optimized scattering structures converge to evident periodical patterns as one would expect for coupling of incident plane wave to the discrete photonic modes. Similar structures can be found in many of the light trapping structure design in the literature⁴. The results are also illustrated by Fourier transformations of the scattering patterns, shown in Fig. 3(c), (f), (i) and (l), with the circles representing the first two fundamental TM modes supported in the slot waveguide for each wavelength. These in-plane wave vectors are determined as the result of scattering layer under normal incidence. In Fig. 3(f), (i) and (l), the overlap between the modes and coupling channels provided by the scattering layer manifests the effective mode couplings. In comparison, the initial random pattern shown in Fig. 3(c) does not provide any strong effective coupling channels. Absorption coefficient of the initial patterns and optimized patterns for incident wavelength 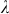= 400 nm, 500 nm and 600 nm are summarized in Table 1. It should be noted that the optimized absorption for 500 nm incidence is low compared with the other wavelengths due to the deconstructive interference in this multi-layered structure. Interestingly, starting from a random pattern, the natural inspired topology optimization process leads to the well-defined scattering structures featuring distinguished scattering orders that match the discrete slot waveguide modes. Furthermore, it is worthwhile to note that the optimized results exhibit appreciable topological variations, suggesting the potential to use this method for searching the optimal light trapping structure beyond a pre-defined topology.

Figure 3. Results of the first optimization case, where the refractive index of the scattering dielectric material n = 1.7.

Unit cell and 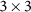cells of the scattering pattern for three different wavelengths of incident light are shown with black and white denoting dielectric material and air, respectively. The Fourier transformation of the scattering patterns are calculated and two fundamental TM modes of the slot waveguide (1^st TM mode: yellow and 2^nd TM mode: blue) are plotted in Fourier space, indicating the mode coupling between incident light and guided modes in slot waveguide. (a) (b) (c) A typical scattering pattern in 1^st generation of optimization. (d) (e) (f) Results of optimized scattering pattern for incident wavelength 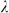= 400 nm. (g) (h) (i) Results of optimized scattering pattern for incident wavelength 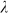= 400 nm. (j) (k) (l) Results of optimized scattering pattern for incident wavelength 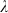= 400 nm.

Table 1. Absorption coefficient of 1^st generation and optimized patterns for incident wavelength 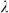= 400 nm, 500 nm and 600 nm.

Targeted Wavelength (nm)	400	500	600
Average absorption coefficient of 1st generation	0.012	0.011	0.016
Absorption coefficient of the optimized pattern	0.829	0.026	0.499

The 2^nd test case for optimization at single wavelength

In the next case, the dielectric material in scattering layer is replaced with high index dielectric (GaP), which is identical to the material used for the cladding layer. While the overall absorbing performance can be improved, the use of high-index dielectric material in the scattering layer leads to a more complicated optimization problem with multiple governing factors in effect. In this case, the scattering layer with proper spatial filling ratio of the dielectric material determines the reflection of the incident light due to the impedance mismatch and the simultaneous diffraction to the targeted slot waveguide modes. Due to the fact that the geometry (topology) change on the scattering layer has a significant influence on both diffraction and reflection, those two competing processes need to be addressed simultaneously during the design process. Competition between these two factors brings forth a large number of local optima, which unfortunately increases the complexity of solution space along with the large design dimensionality, all together resulting into the ill-posedness of the problem⁴⁹, i.e. non-existence of solution. Moreover, as rooted in its stochastic characteristic, GA based NGTO is vulnerable to “structural noise”⁵¹ in that checkerboard patterns and redundant small scale features appear during optimization iterations and in the final results. They exhibit limited contribution to absorption enhancement while dramatically increase the difficulty in the device fabrication.

To overcome the aforementioned numerical instabilities, we introduced the filtering technique³⁴ into the GA based NGTO method. Inspired from the image processing field, filtering techniques have been wildly adopted in gradient based topology optimization³⁴,⁵². During the density filtering process, the original field of design variables is smoothened by modifying the value of design variable in each element according to its neighborhood values. The smoothened field is then converted into a binary-valued field by comparing with a threshold value⁵³. While preserving the general geometric property, instable features are effectively removed after filtering. In the optimization process with density filtering as shown in Fig. 2(a), original element densities are referred to as design variables, and actual designs are presented in the form of filtered element densities that carry physical meanings.

Observing the diagonal symmetry of optimized patterns shown in Fig. 3 under the polarization condition, the D₄ symmetry was imposed to constraint the unit cell for faster optimization convergence. In this case, the design space is reduced to the area denoted by the dash-lined triangles in Fig. 4(a), (e) and (i). The optimized scattering patterns of the unit cell as well as the expanded domain consisting 3×3 unit cells for incident wavelength of 400 nm, 500 nm and 600 nm are shown in Figures 4(a) and (f), (b) and (i), (e) and (j), respectively. Optimized patterns obtained are of complicated topology. To further illustrate the optimization results, Fourier transformation of each optimized pattern and two fundamental TM modes are shown in Fig. 4(c), (g) and (k), respectively. Mismatch of the scattering channels and slot waveguide modes is observed from the Fourier transformation, which reveals mode coupling condition is not fully satisfied. This manifests the fact that optimization in this case is a tradeoff between diffraction and reflection, leading to the complicated topology beyond the reach of parametric design. Absorption spectra for the scattering layer optimized at wavelength of 400 nm, 500 nm and 600 nm are shown in Fig. 4(d), (h) and (l), respectively. Distinctive absorption peaks at each target wavelength illustrate the effectiveness of the optimization. The absorption and enhancement factor of the optimized structure for each wavelength are shown in Table 2. The absorptions of all optimized designs are above 0.96, with the highest value reaching 0.99 without using the back reflector. These results reveal that both reflection and transmission are eliminated and the whole diffraction energy is absorbed by the active layer through optimization. The enhancement factor, defined as the ratio between the total absorption and the single-path absorption for each wavelength, is shown in Table 2. Single-path absorption 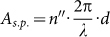, where 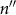is the imaginary part of the refractive index of the active layer and 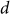is the thickness of the active layer⁵. In this case, the enhancement factor of the optimized patterns achieved for each wavelength exceeds the Yablonovitch Limit, which is 7.22 without back reflector.

Figure 4. Results of the second optimization case, where the refractive index of the dielectric material in the scattering layer n = 1.7.

Unit cell and 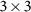cell of the scattering pattern for three different wavelengths of incident light are shown with black and white denoting dielectric material and air, respectively. The Fourier transformation of the scattering patterns are calculated and two fundamental TM modes of the slot waveguide (1^st TM mode: yellow and 2^nd TM mode: blue) are plotted in Fourier space, indicating the mode coupling between incident light and guided modes in slot waveguide. The absorption spectrum from 300 nm to 700 nm of the optimized scattering pattern is presented. The red and blue dash lines indicate the targeted wavelength and average absorption coefficient, respectively. (a) (b) (c) (d) Results of optimized scattering pattern for incident wavelength 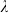= 400 nm. (e) (f) (g) (h) Results of optimized scattering pattern for incident wavelength 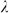= 500 nm. (i) (j) (k) (l) Results of optimized scattering pattern for incident wavelength 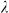= 600 nm.

Table 2. Absorption coefficient and enhancement factor of optimized patterns for 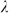= 400 nm, 500 nm and 600 nm.

Wavelength (nm)	400	500	600
Absorption coefficient	0.964	0.985	0.991
Enhancement factor	39.61	50.67	60.78

Broadband optimization for solar spectrum

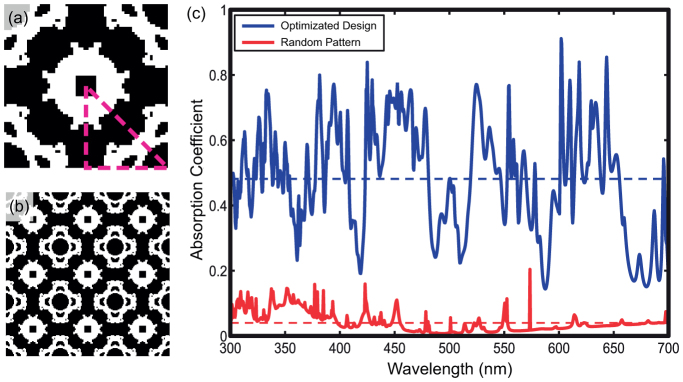
Finally, an optimization of light trapping structure over the broad visible spectrum from 300 nm to 700 nm has been performed. Designing proper scattering patterns for broadband performance becomes even more complicated than for a single wavelength. As slot waveguide supports discrete resonances, the spectral absorption depends on contributions from the aggregated resonances. It is expected that the overall spectral absorption can be enhanced with the improvement of absorption of multiple wavelengths. Therefore, 31 wavelengths evenly distributed in the spectrum are considered in this broadband optimization. The optimized pattern and the spectral absorption from 300 nm to 700 nm are shown in Fig. 5(a), (b) and (c). The average absorption over the whole spectrum reaches 0.481, with enhancement factor 24.4, which is above three times the Yablonovitch Limit at normal incidence. For comparison, the spectral absorption of the random scattering layer using the same material is depicted in Fig. 5(c). In contrast to both the strong coupling to slot waveguide modes and reduction of reflection from optimized scattering patterns, the random scattering pattern provides a continuum of wave vectors and results into much lower absorption 0.04 and enhancement factor 2.03, which is inferior to the Yablonovitch Limit. This demonstrates that without elaborate designs of the scattering layer, slot-waveguide based cells cannot exhibit superior spectral performance.

Figure 5. Results of optimal light trapping structure over the broad visible spectrum from 300 nm to 700 nm.

31 wavelengths evenly distributed in the spectrum are selected in this broadband optimization. (a) Unit cell of the optimized scattering pattern. (b) 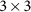cell of the optimized scattering pattern. (c) Absorption spectrum of the optimized scattering pattern (blue solid line) and a typical random scattering pattern (red solid line). Blue and red dash line represents average absorption coefficient of the optimized scattering pattern and the random pattern, respectively.

Discussion

In conclusion, we have extended the topology optimization method to designing light-trapping structure for thin-film cells. Slot-waveguide based thin-film cell is selected as a test case optimized using the GA based NGTO, which is shown to be robust in achieving high-performance designs for problems with complex and highly nonlinear solution spaces. The power of topology optimization method as a structural optimization tool has been demonstrated through the optimized structures of disparate topology for different optimization cases, such as the relatively simple nanowire structure⁴ in Figure 3 or more sophisticated patterns in Figure 4. Substantial enhancement in light absorption has been achieved for different cases, which is beyond the reach of physical intuition or designers' experience and can only be obtained with the aid of the systematic design approach. Broadband optimization with simultaneous consideration of all governing factors over the solar spectrum brings forth a light-trapping structure with enhancement factor over three times the Yablonovitch limit. In the future work, solar spectrum weighted absorption can be assigned as objective function of the optimization. Moreover, it has been reported that structural randomness on different length scales can also contribute to the broadband absorption enhancement⁵⁴,⁵⁵, yet they still need a systematic design approach. In this case, GTO can be implemented for achieving more innovative light-trapping structures with further performance improvement by accommodating more design freedom and extending design space to three dimensions.

Methods

Genetic Algorithm (GA)

For the standard GA in this work, the tournament scheme that has been proved to be more favorable than others is used to perform the selection⁵⁶ and the uniform crossover scheme appropriate for 2D topology optimization problems is adopted²⁸. Values of the control parameters in this standard GA are determined according to the 3-step methodology⁵⁷ to ensure a competent GA optimization. In this work the population size NP, i.e. the number of designs within one generation, is selected to be 2×N (N is the number of design variables, i.e. discretized elements). The total number of evolving generation NG is set as 1.4×NP and the elitism scheme is adopted that the best design within in the present generation is preserved to the next generation. The parameter s for tournament selection scheme, denoting the number of candidate designs in tournament selection, is chosen to be 2. The values of crossover probability Pc and mutation probability Pm are thus chosen to be 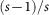and 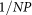, respectively. In the second optimization case where the high-index dielectric material is used for the scattering layer, the density filtering technique³⁴,⁵³ is adopted. As Equation (2), the filtered density field 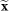carrying physical meanings is calculated as a convolution product of a filter function and the original density field x. The intermediate values produced by the filtering are then avoided by projecting the values above threshold value 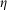to 1 and below 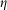to 0. In this work, the filtering length scale r and the projection threshold are set as 2 and 0.5, respectively.

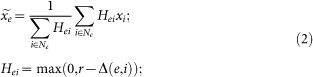Rigorous Coupled Wave Analysis (RCWA)

The absorption is calculated by using RCWA method, which is one of the most commonly used techniques to solve the scattering problem of periodic dielectric structures in Fourier space. For the multilayered dielectric stacks, Fourier expansions of both the field and the permittivity lead to an algebraic eigenvalue system for each layer. The number of Fourier components considered in the optimization process is 13 by 13. The convergence test was performed on the selection of the diffraction order to ensure the numerical accuracy. As the scattering layer is discretized by a 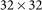grid mesh, the Fourier components of the permittivity can be calculated by

The electromagnetic fields in each layer are determined by solving the eigenvalue problems. The scattering matrix algorithm (S matrix) is then applied on boundary conditions, leading to an S matrix for the configuration under investigation. Poynting theorem is implemented to yield reflection, transmission, and deflection and law of energy conservation implies

where I is the incidence, A is the absorption, R is the zeroth-order reflection, T is the zeroth-order transmission, and D is deflection, which includes higher order reflection and transmission.

Author Contributions

C.S. and W.C. initiated and supervised the project. C.W. performed the RCWA simulation and physical analysis and Y.S.C conducted the optimization. All authors discussed the results and contributed to the manuscript.