Abstract
Excitation–contraction coupling describes the processes relating to electrical excitation through force generation and contraction in the heart. It occurs at multiple levels from the whole heart, to single myocytes and down to the sarcomere. A central process that links electrical excitation to contraction is calcium mobilization. Computational models that are well grounded in experimental data have been an effective tool to understand the complex dynamics of the processes involved in excitation–contraction coupling.
Presented here is a summary of some computational models that have added to the understanding of the cellular and subcellular mechanisms that control ventricular myocyte calcium dynamics. Models of cardiac ventricular myocytes that have given insight into termination of calcium release and interval–force relations are discussed in this manuscript. Computational modeling of calcium sparks, the elementary events in cardiac excitation–contraction coupling, has given insight into mechanism governing their dynamics and termination as well as their role in excitation–contraction coupling and is described herein.
Keywords: Heart, Excitation–contraction coupling, Calcium, Computational model, Calcium spark, Interval–force relation, Calcium wave, Arrhythmia, Drug discovery
1. Introduction
The main function of the heart is to pump blood throughout the body. Blood carries oxygen, hormones, and nutrients to the cells of the body and carries away wastes and carbon dioxide. In this function of the heart, the individual muscle cells called cardiac myocytes contract in a coordinated fashion to achieve this purpose. The contraction of individual myocytes is coordinated by a propagation wave of electrical depolarization of the myocyte cell membranes (sarcolemma). Disruption of this coordinated contraction can impair the heart’s ability to pump blood. To pump blood the heart is divided into four chambers: the right and left atria and the right and left ventricles. The ventricles are the two chambers of the heart that pump blood to the rest of the body.
Computational models of the heart have been used successfully to provide insight into cardiac function. These models describe various aspects of the heart from the subcellular level, to individual cells, to the whole heart. This chapter focuses on the computational modeling of cardiac excitation–contraction coupling in ventricular myocytes. Excitation–contraction coupling are the processes starting with electrical excitation of the sarcolemmal membrane, through calcium mobilization, to contraction. Electrical excitation of the heart starts with a trigger depolarization that results in the opening of voltage-gated ion channels, one of which is the L-type calcium channel which is crucial for excitation–contraction coupling. There are many other proteins that contribute to shaping the action potential including the sodium channel, several types of potassium channels, the sodium–calcium exchanger, and the sarcolemmal calcium ATPase. The coordinated opening and closing of these channels combined with the activation of the pumps and exchangers results in the action potential.
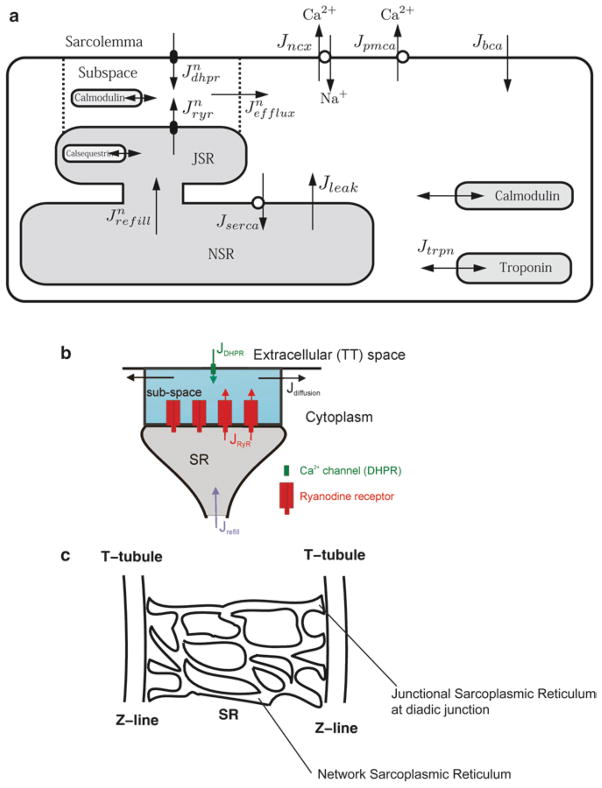
The opening of the L-type calcium channel in response to membrane depolarization allows the passage of calcium ions into the myocyte, mainly into a restricted subspace called the diad (Fig. 1). The diad is formed by the close proximity of the sarcoplasmic reticulum, which is the internal store for calcium, and the t-tubule, which is an extension of the sarcolemma deep into the myocyte. In the diad, these two structures are only 12–15 nm apart. This results in close apposition of the L-type calcium channels that lie in the t-tubule and the ryanodine receptors that lie in the sarcoplasmic reticulum membrane. The ryanodine receptors are ion channels that open in the presence of elevated calcium and release calcium from the junctional sarcoplasmic reticulum. Hence, when calcium enters through L-type channel, it elevates dyadic calcium and triggers the opening of the ryanodine receptors in a process called calcium-induced calcium release. This results in the calcium transient which is a 10–20-fold amplification of the initiating calcium trigger. The elevated calcium binds to calcium-binding proteins in the myocyte such as troponin which is a contractile protein and calmodulin which is a signaling protein. The result of calcium binding to troponin is the initiation of myofilament contraction. Over 90% of the calcium during a transient is bound by calcium-binding proteins which effectively buffers the calcium signal. Calcium is resequestered into the network sarcoplasmic reticulum by the SERCA (sarcoplasmic and endoplasmic reticulum calcium ATPase) and extruded from the myocyte across the sarcolemma by the sodium–calcium exchanger and sarcolemmal calcium ATPase. Calcium in the network sarcoplasmic reticulum diffuses to refill the junctional sarcoplasmic reticulum.
Fig. 1.
Schematic diagram of excitation–contraction coupling in the ventricular myocyte. (a) Excitation–contraction coupling model of the guinea pig ventricular myocyte. (b) Model of the calcium release unit in the diad, (c) sarcoplasmic reticulum arrangement in the sarcomere.
This cycle of calcium triggering, release and uptake, takes place in the approximately 20,000 diad spaces (also called calcium release sites) that are distributed throughout the myocyte (Fig. 1) due to the regular organization of the myocyte into sarcomeres. The sarcomeres are delineated by the z-lines which are visible bands in the myocyte resulting from the localization of the dyadic structures. The process of excitation–contraction hence is a spatially distributed process and calcium release is a local event. During an action potential the membrane depolarization almost instantaneously spreads throughout the sarcolemmal and t-tubular system resulting in well-coordinated calcium release throughout the myocyte. However, under certain conditions such as in resting myocyte (the absence of electrical excitation) or during pathological conditions, there can be non-coordinated release from the different release units. In the resting myocyte, these events occur stochastically and are called calcium sparks which are considered to be the elementary events of excitation–contraction coupling. Under pathological conditions the spontaneous sparks might release enough calcium to diffuse and trigger adjacent sites resulting in a wave of calcium release and a wave of elevated calcium. The calcium wave can result in membrane depolarization and triggering of an aberrant action potential through activation of the sodium–calcium exchange. This is considered to be one mechanism for the generation of cardiac arrhythmia.
In the following sections, methods for developing computational models of excitation–contraction coupling are discussed. These sections demonstrate how insights into mechanisms of cardiac excitation–contraction coupling in ventricular myocytes are formed from the models. They also demonstrate how the models can be used to study cardiac arrhythmia.
2. Materials
Computational modeling of excitation–contraction coupling can be performed using a variety of methods. The model must be solved using either a computational modeling tool or by writing computer code to solve the model using a computer language such as FORTRAN, C, MATLAB, CUDA, etc. Models of excitation–contraction coupling of single myocytes can easily be solved on a desktop computer. Larger models consisting of networks of myocytes might require multiple processors as found in multicore CPUs (Central Processing Units), clusters of CPUs, and more recently in GPGPUs (General Purpose Graphics Processing Units).
3. Methods
3.1. Cardiac Ventricular Myocytes
The cardiac ventricular myocyte contains all the necessary components for cardiac excitation–contraction coupling. This includes ionic homeostasis by pumps and exchangers, sarcolemmal ion channels, calcium release channels in the sarcoplasmic reticulum, and calcium-binding proteins (Fig. 1). The sarcolemma is the outer membrane of the cardiac myocyte that consists mainly of phospholipids, cholesterol, and proteins. Being a lipid bilayer, the membrane does not allow the passage of charged particles such as ions. Ions are transported across the charge-separating lipid bilayer by ionic pumps and exchangers creating an electrochemical gradient across the membrane. The electrochemical gradient is described mathematically by the Nernst potential
| (1) |
where A is the ionic species, R is the ideal gas constant (8.314 J/mol/K), T is the absolute temperature, z is the charge of the ion A, F is Faraday’s constant (96,485 coulombs/mol electrons), and [A]out and [A]in are the concentrations of ion A outside and inside the myocyte, respectively. The result of the different ion distributions is a membrane potential whose value can be calculated by the Goldman–Hodgkin–Katz current equation (Eq. 8).
Ions traverse the membrane in three ways, all mediated by protein complexes (1): ionic pumps consume ATP to move ions up the electrochemical gradient (2). Ion exchangers use the electrochemical gradient of type of ion to transport another ion across the membrane against its electrochemical gradient (3). Ions, such as sodium, potassium, and calcium, traverse the membrane down their electrochemical gradient through ion channels which are proteins that span the sarcolemmal membrane that contain well-regulated, ion-conducting pores. These three mechanisms allow the passage of ions through the membrane in a controlled fashion in response to changes in membrane potential and ligand binding.
3.2. Ion Channels
3.2.1. Deterministic Model
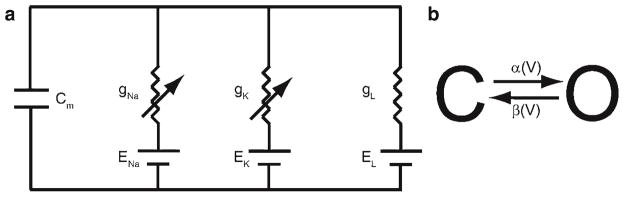
The first modern mathematical description of ion channels was developed by Hodgkin and Huxley to describe the mechanism of action potential propagation in the squid giant axon (1). In their description, the membrane with ion channels was mathematically equivalent to a capacitor and a resistor in parallel (Fig. 2a). By Kirchoff’s Law the sum of currents flowing into a node must be zero. Hence,
Fig. 2.
(a) Circuit diagram of membrane. (b) Simple gating model.
| (2) |
where Icapacitive and Iionic are the currents resulting from the changes to charged ion concentrations on both sides of the membrane (capacitor) and the ionic currents through ion channels, respectively. The channel current can be derived as
| (3) |
| (4) |
where Q is the charge across the membrane, Cm is the membrane capacitance, V is the membrane potential, and Icap is the membrane capacitive current. The ion channels allow the passage of current in the form of ions in different amounts depending upon conditions and are hence described as variable resistors. Hence, for each current
| (5) |
| (6) |
| (7) |
where GA is the conductance (1/RA) for ion A and EA is the reversal or Nernst potential for ion A. It is called the reversal potential because as the membrane potential V crosses V the sign or direction of the current reverses. The ion channels were described as having variable conductance (the reciprocal of resistance) that depends upon what we now call voltage-dependent gates. This is described by representing the total conductance by the maximal conductance gA multiplied by the fraction of open channels o. In the Hodgkin–Huxley model, the three currents used are sodium (Na), potassium (K), and a passive leak. In the equation above, a linear current–voltage relation is used and is a good approximation of experimental data. However, in some cases this is inadequate and the Goldman–Hodgkin–Katz equation is used instead
| (8) |
where PA is the permeability of the channel in m/s, zA is the charge on ion A, and [A]i and [A]o are the intracellular and extracellular concentrations of ion A, respectively. Hodgkin–Huxley descriptions of ion channels are widely used to model ion channel in the heart and are described further.
In the case of the Hodgkin–Huxley model, each channel gate is described by a two-state model (Fig. 2b): a closed state (C) that does not permit the conductance of ionic current and an open state (O) that does with the variables c and o, respectively, to describe the fraction of channels in each state (c + o = 1). From the state diagram, using the same concept as the Law of Mass Action from chemistry a set of differential equations can be derived
| (9) |
| (10) |
or in an alternate form
| (11) |
with o + c = 1, o∞ (V) = α(V)/(α(V) + β(V)), and τ∞(V) = 1/(α(V) + β(V)). This system of ordinary differential equations would be solved by a standard numerical method the Euler method, Runge–Kutta method, or any other such method. Equation for α(V) and β(V) may use the formalism described by Hodgkin and Huxley (1). They applied Boltzmann’s principle which relates the proportion of molecules inside the membrane (Pi) to those outside the membrane (Po) by
| (12) |
where w is the work required to move the molecule from the inside to the outside, z is the charge of the molecule, K is Boltzmann’s constant, and T is absolute temperature. This in essence described the gating charge that was unknown at the time, but has since been described in the scientific literature. The gating charge corresponds to the movement of charged parts of the ion channel that give the channel its dependence on membrane potential. Using the fact that Pi + Po = 1
| (13) |
If z is negative and V sufficiently large
| (14) |
where C is a constant. These types of expressions are used to describe α(V) and β(V).
This formalism has allowed the development of models of the cardiac ventricular myocyte (for review see (2)). Prior to this the first step was the development of the DiFrancesco–Noble model of the Purkinje fiber in 1985 (3). The first computational model of the cardiac ventricular myocyte was developed by Beeler and Reuter (4) built upon the family of model resulting from the DiFrancesco–Noble model. This model added a slow inward potassium current and intracellular calcium concentration changes to these previous efforts. Luo and Rudy provided the first published biophysically detailed and experimentally verified model of the ventricular myocyte (5) based upon guinea pig physiology. They improved upon this in 1994 in their Phase II model (6). This enabled a new family of models, each of which has made a positive contribution to the field (7–10). These models enabled the study of many properties of the ventricular myocyte including the dependence of action potential properties on pacing frequency and how this can contribute to arrhythmia, effect of mutations, and mechanisms of drug action.
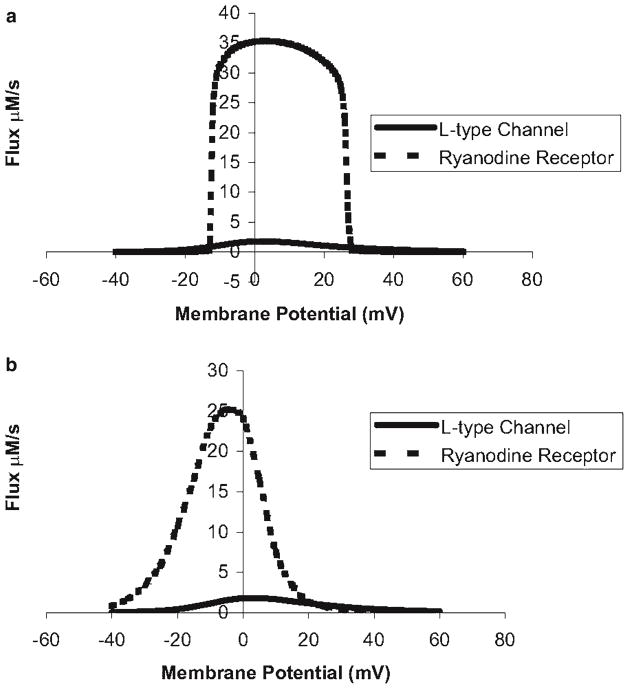
Many of these early models based upon deterministic representations of ion channels group the 20,000 release units into one common pool. As a result, once the ryanodine receptors in this common pool are activated by trigger calcium, the strong positive feedback of calcium-induced calcium release ensures that the pooled release units fully activate. Hence, the models that include a realistic calcium-induced calcium release mechanism display an all-or-none calcium response (Fig. 3). However, in reality, cardiac ventricular myocytes display a graded response to trigger calcium (11, 12). This means that as the amount trigger calcium increases, the amount of release from the internal stores via the ryanodine receptors increases. Some of the computational models do simulate graded release, but require an artificial mechanism, such as tying calcium release to calcium influx to produce a graded response (6). Thus, in spite of the many successes of these models, they fail to capture graded release with a physiological mechanism.
Fig. 3.
(a) The deterministic common pool model of the guinea pig ventricular myocyte does not properly produce graded calcium release. (b) A local control model based on independent stochastic calcium release units that produce calcium sparks successfully produces graded release.
In order to capture graded release, Stern (13) demonstrated with simplified models that graded release could be achieved if the calcium release units were represented by stochastic models. This was later demonstrated in a more physiological model by Rice and coworkers (14). In these models, the stochastic opening of the L-type calcium channels results in the opening of different numbers of channels to produce different level of calcium current. When there is a sufficient rise in dyadic subspace calcium due to local L-type calcium channel opening, the ryanodine receptors in the subspace would open. Hence, the stochastic recruitment of different number of release units results in graded release (Fig. 3). This concept is described by the term local control.
3.2.2. Stochastic Model
Ion channel gating can be described by stochastic models as mentioned above. This reflects the reality that, in microelectrode experiments where they can isolate and observe the current passing through a single ion channel, current measurements show a stochastic opening and closing of channel. These experiments characterize the single channel current, the open probability, and the open and close dwell times (the amount of time a channel remains in the open or close state).
In order to model a channel stochastically, consider the ion channel shown in Fig. 2b. Instead of each state representing the fraction of channels in the open state, the model corresponds to the two possible states of an ion channel. If the rate constants are multiplied by a characteristic time Δt, rates with units of s−1 become unitless transition probabilities (Fig. 4). The choice of Δt is typically small so that a transition occurs only 10% of the time to minimize erroneous transitions. In this model, the next state of the channel depends upon the current state and none of the prior states. This is called the Markov property. As the state the channel assumes is a random process that has the Markov property, it is Markov Chain. The method to simulate the stochastic gating of ion channels is called a Markov Chain Monte Carlo simulation.
Fig. 4.
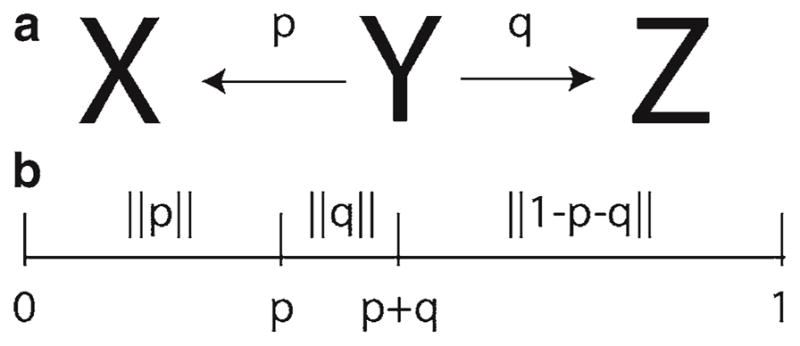
(a) State diagram with possible transitions from state Y to state X or Z. (b) The transition probabilities are mapped to the interval [0,1] for comparison to a uniform [0,1] random number.
In a Markov Chain Monte Carlo simulation, the stochastic transition from the current state to another is determined by comparing the transition probability to a random number on the interval [0,1] (Fig. 4). In the case of ion channel simulations this random number is typically uniformly distributed. If there are more than one possible transition, the transition probabilities are arranged along the interval [0,1] so that they cover a portion of the interval equal to the transition probability. The remaining portion of the interval is the probability of remaining in the same state. The location where the uniform random number falls on the interval determines the next state. This comparison is performed for each of the channels and the number of open channels is computed. This number determines the open probability and is used in calculation of the ionic current
| (15) |
where N is the number of channels and Si is 1 if the ith channel is in the open state and 0 otherwise.
3.3. Calcium Dynamics
Calcium dynamics play a central role in cardiac excitation–contraction coupling as described above. Computational models of calcium dynamics in cardiac cells have added to the understanding of cardiac excitation–contraction coupling. Example modeling approaches for the different components involved in calcium dynamics are presented in the following sections.
3.3.1. L-Type Calcium Channel
The L-type calcium channel opens during depolarization and helps to shape the action potential. It brings calcium ions into the myocyte, mostly into the dyadic subspace where it can trigger release from the ryanodine receptors. The L-type calcium channel opens in response to membrane depolarization and then undergoes a process called inactivation which is a voltage- and calcium-dependent process. Under inactivation, the channel cannot be excited to the open state for a period of time. Early models of the L-type channel were based upon Hodgkin–Huxley-type descriptions with three gates, a voltage-dependent activation gate d, a calcium-dependent inactivation gate fCa, and a time-dependent inactivation gate f. It uses a Goldman–Hodgkin–Katz formalism for channel permeability (Eq. 8). For example, in the Luo–Rudy model (6)
| (16) |
where γCa i and γCa o are the activity coefficients for calcium in the intracellular and extracellular compartments and other variables are as described previously. The d and f gates are described with Hodgkin–Huxley gating and the fCa gate is an instantaneous function of calcium that ranges between 0 and 1
| (17) |
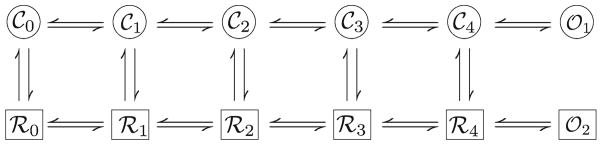
An alternate way of modeling the channel is the use of Markov state models in which the ion channel is assumed to have a number of states with transitions possible between the states. Jafri and coworkers (15) developed such a model of the L-type calcium channel in their model for the guinea pig ventricular myocyte (Fig. 5). The goal of this model was to more accurately capture calcium-dependent inactivation of the channel based upon a mode switching model proposed by Imredy and Yue (16). In mode switching the transitions in a mode are faster (and hence more frequent) than the transitions between modes. The top row of states corresponds to normal mode when the calcium concentration is low. The bottom row, which is reached by calcium-dependent transition, is mode calcium which is reached during periods of elevated calcium concentration.
Fig. 5.
L-type calcium channel model.
The L-type channel consists of four subunits. Each subunit is assumed to be capable of two conformations, permissive and nonpermissive. The horizontal (Fig. 5) voltage-dependent states describe the transition of each subunit of the channel from the no subunits in the permissive state to one permissive subunit to two permissive subunits, to three, and finally four permissive subunits (from left to right). Once all four subunits are in the permissive state, there is a voltage-independent transition to the open state. In mode calcium this transition to the open state is rare, resulting in effectively no channel opening while in this mode. Time-dependent inactivation is captured by a Hodgkin–Huxley gate similar to that used by Luo and Rudy that can be reached from any state in the model. An alternative approach would be to have another level of 12 time-inactivated states, each of which could be reached by corresponding state in the current model.
This type of model results in many possible parameters. Fortunately, the structure of the model allows a logical reduction of number of parameters. For example, the parameter α(V) describes the transition rate for one subunit to transition from permissive to nonpermissive. The parameter β(V) describes the opposite transition. For the transition from Co where all four subunits are in the nonpermissive state to C1 where three subunits are in the nonpermissive state, the rate parameter α(V) is multiplied by a factor of 4 to reflect this. For the reverse transition, the parameter α(V) is multiplied by a factor of 1 as there is only one subunit in the permissive state.
Because this model includes closed circuits, it must satisfy the thermodynamic constraint known as microscopic reversibility. This rule requires that the product of the four rate constants in one direction around the circuit is equal to the product of the four rate constants in the opposite direction around the circuit. This arises from the fact that the equilibrium constant for a reaction ΔGrxn =−RTln(Keq) or Keq = e−ΔGrxn/RT where ΔGrxn is the free energy change of reaction and Keq is the equilibrium constant. Movement around the loop to back to the starting point should entail no change in energy by the Law of Conservation of Energy. Therefore,
| (18) |
In deterministic simulation, differential equations are derived for each state using the Law of Mass Action as described above (Eqs. 9 and 10). In this case each state corresponds to the fraction of channels in that state. Differential equations are only needed for 11 of the states as the 12th state is the sum of the other states subtracted from one. This model can also be used for stochastic simulation, as well, with each state describing the state of an individual channel.
3.3.2. Ryanodine Receptors
Ryanodine receptors are calcium-activated calcium channels that are located in the sarcoplasmic reticulum membrane and are responsible for producing calcium-induced calcium release observed in cardiac myocytes. The cardiac isoform is RyR2 and it is located mostly in the junctional sarcoplasmic reticulum that is found in the diad. In addition to this strong activation by calcium the channels are also regulated by sarcoplasmic reticulum lumenal calcium. Experiments have shown that the ryanodine receptor open probability increases as the lumenal calcium increases (17). The ryanodine receptors also have been observed to display a property called adaptation (18), in which in response to a step increase in calcium, the ryanodine receptor open probability will after a step increase decline slightly to a new steady state. This is similar to a weak and slow inactivation process. Finally, ryanodine receptors are located in clusters in the diad (19). Experiments have suggested that the gating of ryanodine receptors is coupled, i.e., channels open and close in synchrony (20).
Computational models have been developed to describe these aspects of the ryanodine receptors. For example, Keizer and Levine (21) and Keizer and Smith (22) developed a four- and six-state model, respectively, to describe cardiac ryanodine receptor activation and adaptation (Fig. 6a, b). This also accurately captures channel open and close dwell times as well as recovery from adaptation. The system of differential equations can be derived from the state diagram. The Keizer–Levine model was incorporated into the Jafri–Rice–Winslow guinea pig ventricular myocyte model and suggested a possible role for adaptation in interval–force relations (15, 23).
Fig. 6.
Schematic diagrams of ryanodine receptor models. (a) Keizer Levine, (b) Smith-Keizer, (c) Sobie et al., (d) the open rate shifts as the sarcoplasmic reticulum depletes in the Sobie et al. model.
A more recent model of the ryanodine receptor was developed by Sobie and coworkers to describe stochastic gating of the ryanodine receptors and how that gives rise to calcium sparks. This model consists of a closed and open state and captures calcium activation by dyadic subspace calcium, coupled gating, and open probability regulation by sarcoplasmic reticulum lumenal calcium (Fig. 6c, d). In the model, the closing rate was independent of [Ca2+)SS
| (19) |
while the opening rate was a fourth-order function of [Ca2+]SS:
| (20) |
Lumenal Ca2+ influences RyR gating through changes in Km in the above equation. Sensitivity to [Ca2+]SS is a linear, decreasing function of [Ca2+]lumen so that RyR opening is favored when [Ca2+]lumen is high, as suggested by the literature (17).
| (21) |
Coupled gating of RyRs is introduced by multiplying the opening and closing rate constants by cooperativity factors (CFopen for opening and CFclosed for closing) that depend, respectively, on the relative numbers of open and closed channels in the cluster
| (22) |
| (23) |
where Nopen is the number of open RyRs and Nclosed is the number closed RyRs. CFopen and CFclose of are both cooperative in their behavior since the value of either depends on the fraction of open channels. The scaling factor kcoop (equal to unity in control conditions) was introduced so that modification of a single parameter could simulate the effects of reduced coupling between RyRs. A thermodynamically based formulation for coupling in an array of channels has been developed that could be used as an alternative (24).
The calcium release flux from the ryanodine receptors is simply the maximal release flux vRyR multiplied by the fraction of open channels PRyR and the calcium concentration gradient between the junctional sarcoplasmic reticulum [Ca]JSR and dyadic subspace [Ca]SS
| (24) |
3.3.3. SERCA
The sarcoplasmic and endoplasmic reticulum calcium ATPase is a protein complex that pumps calcium into the sarcoplasmic (endoplasmic) reticulum against a concentration gradient using the energy contained in ATP. The cardiac myocytes isoform is SERCA2b and it is localized to the network. In a steadily beating myocyte, the calcium released by the ryanodine receptors is re-sequestered into the sarcoplasmic reticulum by this pump. The pump flux is typically characterized by
| (25) |
where vSERCA is the maximal pump flux, KSERCA is the calcium binding constant to the pump, and [Ca]myo is the myoplasmic calcium concentration. Other formulations for SERCA have been proposed. For example, a more complex, thermodynamically constrained model has been proposed by Tran and coworkers (25).
3.3.4. Calcium Extrusion
Calcium is extruded from the cardiac myocyte mainly by the sodium–calcium exchanger which uses the sodium concentration gradient to transport three sodium ions into the myocyte in exchange for one calcium ion. This results in an inward current due to the net positive charge entering the myocyte. This raises the possibility that large exchanger currents can help to depolarize the myocyte. A typical formulation for the exchanger used in cardiac myocytes is (3, 6)
| (26) |
where kNaCa is the maximal exchanger current, [Na]myo and [Na]o are the myoplasmic and extracellular sodium concentrations, [Ca]o is the extracellular calcium concentration, Km,Ca and Km,Na are the half saturation constants for calcium and sodium, ksat is the saturation factor at very negative potentials, and η is a factor to control the voltage dependence.
The sarcolemmal calcium ATPase plays a minor role in extruding calcium from the myocyte. A typical formulation is
| (27) |
where Ī p(Ca)is the maximal sarcolemmal calcium ATPase current and Km,p(Ca) is the binding constant for calcium to the ATPase.
3.3.5. Buffering
Calcium is highly buffered in living cells through the binding to calcium-binding proteins and negatively charged species in the cell. The likely reason is that calcium ions are involved in regulating and signaling many diverse processes in the cell. In the myocyte, about 90% of the calcium is bound to such buffers. In the cardiac myocyte, the most significant buffers are calmodulin which is a signaling protein and troponin which is a contractile protein. Other significant buffers can be the negative charges associated with cellular membranes (26). Modeling of binding to calcium buffers represents the binding as a biochemical reaction with forward (kf) and backward (kb) rate constants. The amount of calcium bound to each buffer can be calculated by deriving the rate equations governed by mass action.
In some cases, calcium binding to calcium binding sites is considered to be fast compared to other relevant cellular processes. In this case, the rapid equilibrium approximation developed by Wagner and Keizer (27) can be used. In this case, the fluxes on the right-hand side of the myoplasmic calcium concentration differential equation is multiplied by βmyo, the dynamic buffering fraction for the bulk myoplasm given by
| (28) |
| (29) |
Here, is the total myoplasmic buffer concentration, is the half saturation constant for a particular myoplasmic buffer, and Ji are the calcium fluxes.
3.4. Excitation–Contraction Coupling
The basic components or excitation–contraction coupling and their model formulations are described above. In order to study excitation–contraction coupling they have to be combined to form a model for calcium dynamics in the myocyte. This is accomplished by constructing differential equations to describe the dynamics of membrane potential and myoplasmic calcium. For example,
| (30) |
where Jleak is the passive leak out of the sarcoplasmic reticulum, Jxfer is the flux between the dyadic spaces and the myoplasm, Jtrpn is the buffering due to troponin, ICa,b is the background calcium current, and the other fluxes and current are as defined above. The parameter Vmyo is the myoplasmic volume and the parameter Acap is the capacitive membrane surface area. In this example, the passive leak and background calcium current are included as they balance the SERCA pump and sodium–calcium exchange currents at rest. This is a common issue with simplified representations for the pumps and exchangers—in order to capture the dynamic behavior, it is possible that the resting activity is too high. A remedy to this is the use of the Tran et al. formulation for SERCA (25).
3.4.1. Calcium Transients
Calcium transients play a central role in excitation–contraction coupling. It provides calcium that is necessary for contraction as well as other possible signaling roles. The calcium transient also influences the action potential through processes such as sodium–calcium exchange and calcium-dependent inactivation of the L-type current.
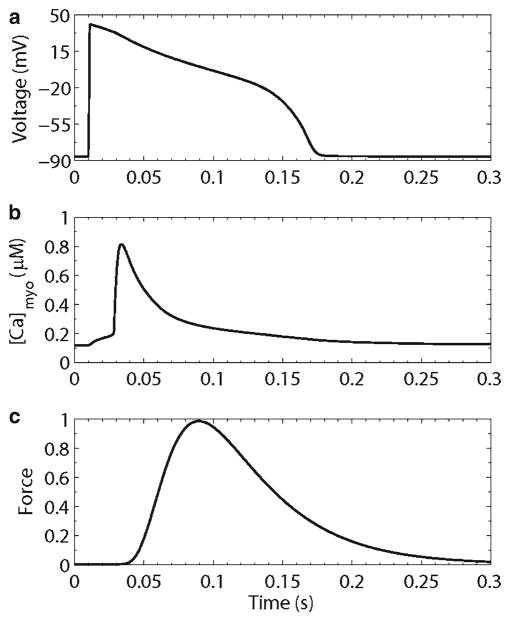
Figure 7 shows an example behavior of the Jafri–Rice–Winslow guinea pig ventricular myocyte model. The model produces reasonable action potentials and calcium transients, and predicts changes in dyadic subspace and sarcoplasmic reticulum calcium concentrations. The model also predicted a mechanism for termination of calcium release. This was an open question because due to the strong positive feedback of calcium-induced calcium release, it was not well understood how release would terminate. The model suggested that reduction of sarcoplasmic reticulum calcium resulted in a sufficient decrease in ryanodine receptor release flux to make calcium-induced calcium release no longer sustainable (15). This reduction of release flux does not require complete emptying of the sarcoplasmic reticulum.
Fig. 7.
Simulated excitation–contraction coupling in the guinea pig ventricular myocyte. (a) Action potential, (b) myoplasmic calcium transient, (c) isometric force transient.
3.4.2. Interval–Force Relations
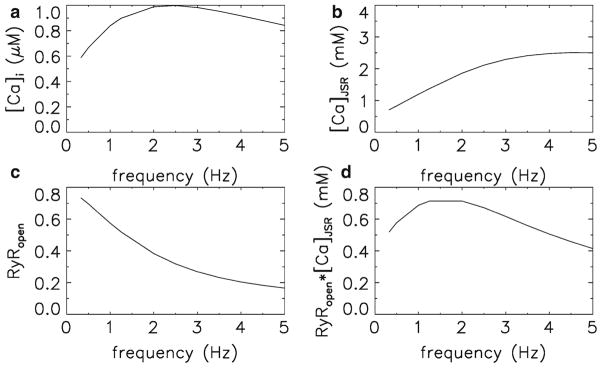
Interval–force relations are an important property of cardiac myocytes and tissue because they describe how the force generated by the heart varies with changes in the pacing frequency. The ability to capture these dynamics is a success of the Jafri–Rice–Winslow models and descendants that was not achieved with previous models. The model not only simulates these behaviors, but it also suggests the mechanisms behind them as well. One such relation is the force–frequency curve, which in guinea pig has a dome shape that peaks at ~2.0 Hz as does cat and human (28, 29). To generate Fig. 8 the model was paced at various frequencies from 0.33 to 5.0 Hz for 30 s each to allow the model to come to a steady train of calcium transients. The peak values of the calcium transients are plotted in Fig. 8a, and they produce a dome-shaped curve. Since force generation is monotonically related to calcium concentration, this reflects the dome-shaped force curve. The mechanism behind this shape is the interplay between the increase of the sarcoplasmic reticulum calcium concentration with increasing pacing rate (Fig. 8b) and the accumulation of the ryanodine receptor in the adapted state as the pacing frequency increases which results in a lower peak open probability (Fig. 8c). Since the ryanodine receptor release flux near its peak is effectively the product between the peak open probability and the junctional SR calcium concentration (Eq. 24), this reflects the mechanism giving rise to the dome shape (Fig. 8d).
Fig. 8.
Interval–force relations. (a) Peak myoplasmic calcium, (b) peak sarcoplasmic reticulum calcium concentration, (c) peak ryanodine receptor open probability, (d) peak ryanodine receptor release flux.
3.4.3. Calcium Sparks
Calcium sparks are considered to be the elementary calcium release events that underlie excitation–contraction coupling. Sobie and coworkers developed a model of calcium sparks to describe their mechanism. This model included the stochastic model of the calcium release channel described above (Eqs. 19–29) that included large numbers of ryanodine receptors, calcium activation of ryanodine receptors, lumenal regulation of ryanodine receptor open probability, and couple gating of ryanodine receptors. The model demonstrated that spark activation was due to calcium-induced calcium release after the stochastic opening of a release channel. Furthermore, changes in sarcoplasmic reticulum lumenal calcium alter the probability of seeing sparks (and spontaneous spark rate as well).
The model also suggested a mechanism for spark termination. This is an extension of the search for the mechanism behind the termination of calcium release during a calcium transient as the calcium transients are composed of numerous calcium sparks. Previously three mechanisms had been proposed for the termination. The first suggested that the sarcoplasmic reticulum emptied so that there was no longer calcium available for release. This is implausible as it is possible with the addition of ryanodine to get sparks to last more than a second which is considerably longer than the 20–30 ms duration of the typical spark (30). Furthermore, after a triggered calcium transient, it is still possible to release calcium with caffeine, which increases ryanodine receptor open probability. This suggests that there is still releasable calcium after a calcium transient.
The second hypothesis suggests that calcium release terminates due to inactivation of the ryanodine receptor (31). However, inactivation has not been observed experimentally under physiologically relevant time and concentration scales. For example, adaptation occurs with a time constant of approximately 150 ms (32). A spark terminates in 20–30 ms, which is too fast for adaptation to be the primary causative factor.
A third mechanism is that the clusters of ryanodine receptors close stochastically through a process called stochastic attrition (13). This is possible for a small number of ryanodine receptors (<6), but is not possible for larger clusters (13, 33). In heart, between 30 and 300 ryanodine receptors have been observed in the dyadic cleft (19).
The spark model also called “the sticky cluster” model presents a novel mechanism for spark termination. Upon cluster activation, almost all the ryanodine receptors open (Fig. 9). The ensuing release flux quickly depletes the junctional sarcoplasmic reticulum. This reduces the ryanodine receptor opening rate (Fig. 6d). As a result, when the individual channels stochastically close, they do not reopen. When enough channels accumulate in the closed state, cooperativity increases the closing of the other channels until release terminates.
Fig. 9.
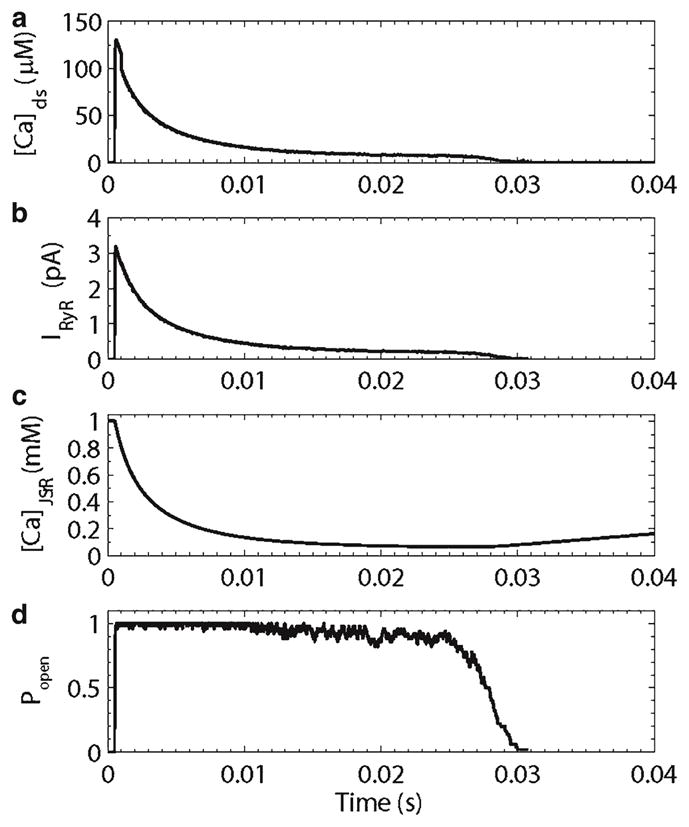
Simulated calcium spark. (a) Diadic subspace calcium concentration, (b) ryanodine receptor release current, (c) junctional sarcoplasmic reticulum calcium concentration, (d) ryanodine receptor open probability.
3.4.4. Graded Release
Graded release is the property that as the trigger calcium increases, the amount of calcium release from the sarcoplasmic reticulum via the ryanodine receptors also increases. This was first observed by Fabiato (12) in skinned cardiac muscle fibers (the sarcolemmal was mechanically removed). This enables the control of the calcium concentration seen by the ryanodine receptors in the diads. This was also reported in individual myocytes in terms of trigger influx through the L-type calcium channel and the resulting ryanodine receptor calcium flux (11).
Deterministic computational models that include the ryanodine receptors in a “common pool” and that have included the strong positive feedback of calcium-induced calcium release have had difficulty modeling graded release and instead shows an all-or-none response (13) (Fig. 3a). This is because once the ryanodine receptors are activated, their calcium release will completely activate all of the ryanodine receptors. Niggli and Lederer suggested that local control, i.e., the stochastic recruitment of individual release units is determined by the total amount of trigger L-type calcium current. The total amount of L-type current depends upon the number of L-type calcium channels activated. This idea was first demonstrated by Stern in a simple model of calcium release, and verified by Rice–Jafri–Winslow in a biophysically detailed model. This was demonstrated to hold with stochastic recruitment of calcium sparks and hence provided the most realistic description of graded calcium release to date (2)(Fig. 3b).
3.5. Cardiac Tissue
Models of cardiac ventricular myocytes can be combined into multicellular networks of cardiac myocytes to simulate sections of cardiac tissues. These types of studies have been extended all the way up to the whole heart (34). There are two basic approaches to do this using the bi-domain model or a mono-domain model. In the bi-domain model, both the intracellular and extracellular spaces are modeled as conducting the spread (or diffusion) of voltage. In the mono-domain model, the extracellular space is assumed to be infinitely conductive, so only the spread of voltage in the intracellular space. This is the approach used by Hodgkin and Huxley in modeling the squid giant axon which was the first model of action potential propagation (1). By Kirchoff’s Law the diffusive current Idiffusive is given by
| (31) |
| (32) |
In the case of a network of cardiac myocytes one might consider the diffusive current to be governed by the connections between cardiac myocytes. In this approach the cardiac myocytes are electrically connected by a coupling current (Igap) that represents the gap junctions that electrically couple the cells in vivo since these are the rate-determining components for the spread of voltage in heart tissue.
| (33) |
where Vi and Vj are two adjacent cells and ggap is the coupling conductance. Typically the coupling conductance is chosen to provide realistic action potential wave propagation velocities.
Over the years knowledge of the diversity of myocytes in the heart as well as the complexity of the microanatomy of the heart has grown substantially. The heart consists of muscle fibers and sheets of muscle fibers that form layers of the heart wall. Models have been developed to include these microanatomical features in addition to electrical and mechanical dynamics of the heart. For example, many outstanding reviews have been written about work in this area (35–38).
3.6. Arrhythmias
Cardiac arrhythmia occurs when the normal depolarization and repolarization pattern of the heart is disrupted. Arrhythmia can have a number of causes including conduction-based arrhythmias, defects in cell excitability, and defects in calcium dynamics. The latter are discussed briefly here.
One of the mechanisms of calcium arrhythmias are the generation of early after depolarizations and delayed after depolarizations. Early after depolarization is an addition depolarization or re-excitation of the membrane potential late in the action potential. A delayed after depolarization is a re-excitation of the membrane and resulting action potential after the conclusion of the action potential. These events are outside the normal heart rhythm. As a result a misplaced action potential can generate a spreading wave of depolarization outside the normal coordinated depolarization wave seen during normal function. This can then disrupt the coordinated depolarization as when two action potential waves collide they annihilate each other. The result is abnormal contraction and a possible disruption of the pumping of blood.
Deterministic computational models of excitation–contraction coupling have been used to study the mechanism and consequences of such events (10, 39). It has been suggested that abnormal calcium release events lead to an aberrant calcium transient. This calcium transient activated sodium–calcium exchange which depolarizes the sarcolemmal membrane. If this depolarization is sufficient, it can excite the sodium and/or L-type calcium channels resulting in an action potential.
One of the possible mechanisms though to be behind these aberrant calcium release events are calcium waves. Calcium waves have been in ventricular myocytes under the pathological condition known as calcium overload. In calcium overload, the myocyte calcium content is elevated. This typically manifests itself by elevated resting myoplasmic and sarcoplasmic reticular calcium concentrations. This can be produced by rapid pacing of the myocyte, especially under conditions of high extracellular calcium. It can also occur during heart failure.
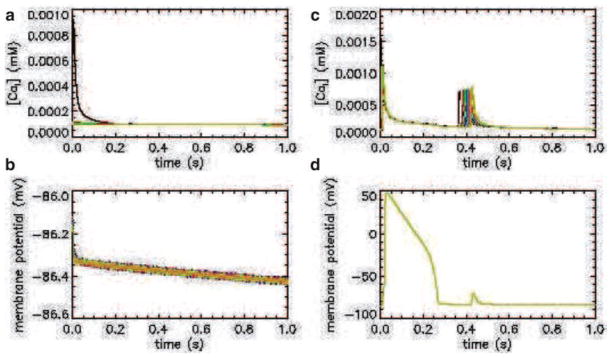
Using the Jafri–Rice–Winslow model of the guinea pig ventricular myocyte, a one-dimension string of myocytes was created. When a calcium release event is simulated in one of the cells, under normal conditions, the calcium concentration (Fig. 10a) and membrane potential (Fig. 10b) remain at a normal level. However, if the myocytes display pathological conditions such as increased sarcoplasmic reticulum calcium concentration and ryanodine receptor hypersensitivity to calcium, a calcium wave occurs (Fig. 10c). If the sodium–calcium exchanger activity is augmented, a propagating wave of depolarization occurs followed by a delayed after depolarization (Fig. 10d). These three conditions are common characteristics of a cardiac myocyte during the conditions known as heart failure. Hence, the model suggests a potential role for the combination of these factors that might give rise to an arrhythmogenic calcium wave.
Fig. 10.
Simulated calcium and membrane potential transients (top and bottom rows, respectively) for a one-dimensional spatial model of a normal and pathological guinea pig ventricular myocyte (left and right columns, respectively).
3.6.1. Mutation
There are many diseases that have been associated with mutations. Mutations are often single-nucleotide mutations (SNPs) in the DNA that result in altered protein sequence, structure, and function. Some of these mutations can lead to cardiac arrhythmias (40, 41). In many cases the changes to channel function caused by mutation have been characterized. Computational models can be used to explore how these mutations contribute to the pathological phenotype by using models of mutated channels in the excitation–contraction coupling models (42–45). These studies can suggest ways in which to compensate for the effect of the mutation to give a more normal phenotype. One possible way might be to target a drug to alter the behavior of the pathological channel. Another might be to use drugs to cause compensatory changes in the behavior of other channels.
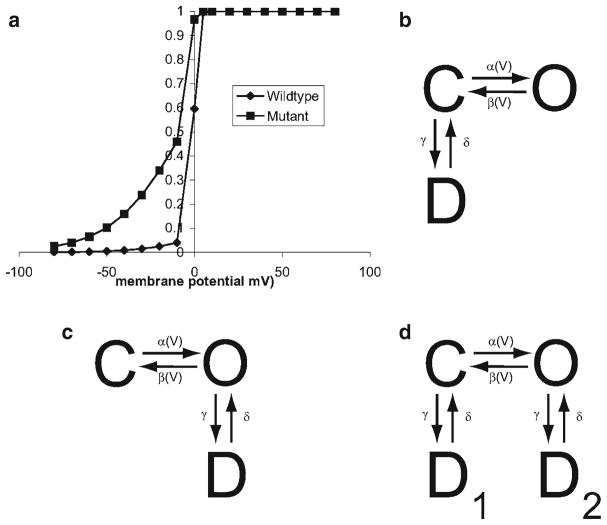
For example, a hypothetical cardiac ion channel that carries inward (depolarizing) current is shown in Fig. 11a. The mutant channel has an increased steady-state open probability over the wild type. This might result in increased activity that might cause increased excitability and/or prolonged action potentials. One way to predict the role is to incorporate both the wild-type and mutant channels in a computational model of cardiac excitation–contraction coupling and observe the changes to the action potential and calcium dynamics. This myocyte model can be incorporated in a network simulation of cardiac tissue to study the arrhythmic potential of this mutant under various simulated conditions.
Fig. 11.
(a) Wild-type and mutant steady-state activation curves for a hypothetical channel. (b) Nonuse-dependent block by drug. (c) Use-dependent block by drug. (d) Use-independent block by drug.
To accomplish the first goal is to develop a model of the channel. This channel can be described by a two-state model as shown in Fig. 2b. The resulting equations governing α(V) and β(V) for the wild type are
| (34) |
| (35) |
which follow the formalism described by Hodgkin and Huxley (1) that would be constrained by experimental data. The mutant channels have a similar description with modified opening rate
| (36) |
| (37) |
3.7. Drug Action
The action of drugs on ion channels can be modeled if the experimental effect of the drug has been characterized. Using this data, a new set of states can be added to a channel model to indicate the drug bound states. These drug bound states should be constrained by kinetic and dose–response experimental studies. These studies also may indicate whether the drug is use or nonuse dependent. Nonuse dependent means that it binds the closed state of the channel (Fig. 11b). Use dependence means that the drug binds the open channel (Fig. 11c). The drug binding to the channel can also be independent of use such that it binds both closed and open states of the channel (Fig. 11d). These approaches have been used to study how drug action might be used to treat cardiac arrhythmia (46). For example, a drug that blocks the channel shown in Fig. 11a might reduce the channel current and return suppress potential cardiac arrhythmia. The potential efficacy of different types of drugs that block the ion channel shown in Fig. 11 can be tested using these types of computational models of drug binding.
4. Notes
Presented here are examples that demonstrate the concepts of using computational models to understand excitation–contraction coupling under normal and pathological conditions. These insights as well as targeted models can aid in the development of novel therapeutics (drugs and devices) that can aid patients with cardiac abnormalities. It is by no means a comprehensive review of the large body of models that have contributed in these areas.
References
- 1.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Williams GS, Smith GD, Sobie EA, Jafri MS. Models of cardiac excitation–contraction coupling in ventricular myocytes. Math Biosci. 2010;226:1–15. doi: 10.1016/j.mbs.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.DiFrancesco D, Noble D. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos Trans R Soc Lond B Biol Sci. 1985;307:353–398. doi: 10.1098/rstb.1985.0001. [DOI] [PubMed] [Google Scholar]
- 4.Beeler GW, Reuter H. Reconstruction of the action potential of ventricular myocarial fibres. J Physiol. 1977;268:177–210. doi: 10.1113/jphysiol.1977.sp011853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Luo CH, Rudy Y. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ Res. 1991;68:1501–1526. doi: 10.1161/01.res.68.6.1501. [DOI] [PubMed] [Google Scholar]
- 6.Luo CH, Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res. 1994;74:1071–1096. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- 7.Livshitz LM, Rudy Y. Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of CAMKII and repolarizing currents. Am J Physiol Heart Circ Physiol. 2007;292:H2854–H2866. doi: 10.1152/ajpheart.01347.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Faber GM, Silva J, Livshitz L, Rudy Y. Kinetic properties of the cardiac L-type Ca2+ channel and its role in myocyte electrophysiology: a theoretical investigation. Biophys J. 2007;92:1522–1543. doi: 10.1529/biophysj.106.088807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Decker KF, Heijman J, Silva JR, Hund TJ, Rudy Y. Properties and ionic mechanisms of action potential adaptation, restitution, and accommodation in canine epicardium. Am J Physiol Heart Circ Physiol. 2009;296:H1017–H1026. doi: 10.1152/ajpheart.01216.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeng J, Rudy Y. Early afterdepolarizations in cardiac myocytes: mechanism and rate dependence. Biophys J. 1995;68:949–964. doi: 10.1016/S0006-3495(95)80271-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Barcenas-Ruiz L, Wier WG. Voltage dependence of intracellular [Ca2+]i transients in guinea pig ventricular myocytes. Circ Res. 1987;61:148–154. doi: 10.1161/01.res.61.1.148. [DOI] [PubMed] [Google Scholar]
- 12.Fabiato A. Time and calcium dependence of activation and inactivation of calcium-induced release of calcium from the sarcoplasmic reticulum of a skinned canine cardiac Purkinje cell. J Gen Physiol. 1985;85:247–289. doi: 10.1085/jgp.85.2.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stern MD. Theory of excitation–contraction coupling in cardiac muscle. Biophys J. 1992;63:497–517. doi: 10.1016/S0006-3495(92)81615-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rice JJ, Jafri MS, Winslow RL. Modeling gain and gradedness of Ca2+ release in the functional unit of the cardiac diadic space. Biophys J. 1999;77:1871–1884. doi: 10.1016/s0006-3495(99)77030-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jafri MS, Rice JJ, Winslow RL. Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys J. 1998;74:1149–1168. doi: 10.1016/S0006-3495(98)77832-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imredy JP, Yue DT. Mechanism of Ca(2+)-sensitive inactivation of L-type Ca2+ channels. Neuron. 1994;12:1301–1318. doi: 10.1016/0896-6273(94)90446-4. [DOI] [PubMed] [Google Scholar]
- 17.Gyorke I, Gyorke S. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+ involves luminal Ca2+ sensing sites. Biophys J. 1998;75:2801–2810. doi: 10.1016/S0006-3495(98)77723-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gyorke S, Fill M. Ryanodine receptor adaptation: control mechanism of Ca(2+)-induced Ca2+ release in heart. Science. 1993;260:807–809. doi: 10.1126/science.8387229. [DOI] [PubMed] [Google Scholar]
- 19.Franzini-Armstrong C, Protasi F, Ramesh V. Shape, size, and distribution of Ca(2+) release units and couplons in skeletal and cardiac muscles. Biophys J. 1999;77:1528–1539. doi: 10.1016/S0006-3495(99)77000-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Marx SO, Gaburjakova J, Gaburjakova M, Henrikson C, Ondrias K, Marks AR. Coupled gating between cardiac calcium release channels (ryanodine receptors) Circ Res. 2001;88:1151–1158. doi: 10.1161/hh1101.091268. [DOI] [PubMed] [Google Scholar]
- 21.Keizer J, Levine L. Ryanodine receptor adaptation and Ca2+(−)induced Ca2+ release-dependent Ca2+ oscillations. Biophys J. 1996;71:3477–3487. doi: 10.1016/S0006-3495(96)79543-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Keizer J, Smith GD. Spark-to-wave transition: saltatory transmission of calcium waves in cardiac myocytes. Biophys Chem. 1998;72:87–100. doi: 10.1016/s0301-4622(98)00125-2. [DOI] [PubMed] [Google Scholar]
- 23.Rice JJ, Jafri MS, Winslow RL. Modeling short-term interval-force relations in cardiac muscle. Am J Physiol Heart Circ Physiol. 2000;278:H913–H931. doi: 10.1152/ajpheart.2000.278.3.H913. [DOI] [PubMed] [Google Scholar]
- 24.Groff JR, Smith GD. Ryanodine receptor allosteric coupling and the dynamics of calcium sparks. Biophys J. 2008;95:135–154. doi: 10.1529/biophysj.107.119982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tran K, Smith NP, Loiselle DS, Crampin EJ. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca(2+) (SERCA) pump. Biophys J. 2009;96:2029–2042. doi: 10.1016/j.bpj.2008.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Smith GD, Keizer JE, Stern MD, Lederer WJ, Cheng H. A simple numerical model of calcium spark formation and detection in cardiac myocytes. Biophys J. 1998;75:15–32. doi: 10.1016/S0006-3495(98)77491-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wagner J, Keizer J. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys J. 1994;67:447–456. doi: 10.1016/S0006-3495(94)80500-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Buckley NM, Penefsky ZJ, Litwak RS. Comparative force–frequency relationships in human and other mammalian ventricular myocardium. Pflugers Arch. 1972;332:259–270. doi: 10.1007/BF00588574. [DOI] [PubMed] [Google Scholar]
- 29.Hasenfuss G, Reinecke H, Studer R, Meyer M, Pieske B, Holtz J, Holubarsch C, Posival H, Just H, Drexler H. Relation between myocardial function and expression of sarcoplasmic reticulum Ca(2+)-ATPase in failing and nonfailing human myocardium. Circ Res. 1994;75:434–442. doi: 10.1161/01.res.75.3.434. [DOI] [PubMed] [Google Scholar]
- 30.Cheng H, Lederer WJ, Cannell MB. Calcium sparks: elementary events underlying excitation–contraction coupling in heart muscle. Science. 1993;262:740–744. doi: 10.1126/science.8235594. [DOI] [PubMed] [Google Scholar]
- 31.Stern MD, Song LS, Cheng H, Sham JS, Yang HT, Boheler KR, Rios E. Local control models of cardiac excitation-contraction coupling. A possible role for allosteric interactions between ryanodine receptors. J Gen Physiol. 1999;113:469–489. doi: 10.1085/jgp.113.3.469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Valdivia HH, Kaplan JH, Ellis-Davies GC, Lederer WJ. Rapid adaptation of cardiac ryanodine receptors: modulation by Mg2+ and phosphorylation. Science. 1995;267:1997–2000. doi: 10.1126/science.7701323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sobie EA, Dilly KW, dos Santos Cruz J, Lederer WJ, Jafri MS. Termination of cardiac Ca(2+) sparks: an investigative mathematical model of calcium-induced calcium release. Biophys J. 2002;83:59–78. doi: 10.1016/s0006-3495(02)75149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Winslow RL, Scollan DF, Holmes A, Yung CK, Zhang J, Jafri MS. Electrophysiological modeling of cardiac ventricular function: from cell to organ. Annu Rev Biomed Eng. 2000;2:119–155. doi: 10.1146/annurev.bioeng.2.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Trayanova NA. Whole-heart modeling: applications to cardiac electrophysiology and electromechanics. Circ Res. 2011;108:113–128. doi: 10.1161/CIRCRESAHA.110.223610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Silva JR, Rudy Y. Multi-scale electro-physiology modeling: from atom to organ. J Gen Physiol. 2010;135:575–581. doi: 10.1085/jgp.200910358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hunter PJ, Pullan AJ, Smaill BH. Modeling total heart function. Annu Rev Biomed Eng. 2003;5:147–177. doi: 10.1146/annurev.bioeng.5.040202.121537. [DOI] [PubMed] [Google Scholar]
- 38.McCulloch AD, Paternostro G. Cardiac systems biology. Ann N Y Acad Sci. 2005;1047:283–295. doi: 10.1196/annals.1341.025. [DOI] [PubMed] [Google Scholar]
- 39.Luo CH, Rudy Y. A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ Res. 1994;74:1097–1113. doi: 10.1161/01.res.74.6.1097. [DOI] [PubMed] [Google Scholar]
- 40.Priori SG. The fifteen years of discoveries that shaped molecular electrophysiology: time for appraisal. Circ Res. 2010;107:451–456. doi: 10.1161/CIRCRESAHA.110.226811. [DOI] [PubMed] [Google Scholar]
- 41.Roberts JD, Gollob MH. The genetic and clinical features of cardiac channelopathies. Future Cardiol. 2010;6:491–506. doi: 10.2217/fca.10.27. [DOI] [PubMed] [Google Scholar]
- 42.Clancy CE, Rudy Y. Na(+) channel mutation that causes both Brugada and long-QT syndrome phenotypes: a simulation study of mechanism. Circulation. 2002;105:1208–1213. doi: 10.1161/hc1002.105183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nuyens D, Stengl M, Dugarmaa S, Rossenbacker T, Compernolle V, Rudy Y, Smits JF, Flameng W, Clancy CE, Moons L, Vos MA, Dewerchin M, Benndorf K, Collen D, Carmeliet E, Carmeliet P. Abrupt rate accelerations or premature beats cause life-threatening arrhythmias in mice with long-QT3 syndrome. Nat Med. 2001;7:1021–1027. doi: 10.1038/nm0901-1021. [DOI] [PubMed] [Google Scholar]
- 44.Clancy CE, Rudy Y. Cellular consequences of HERG mutations in the long QT syndrome: precursors to sudden cardiac death. Cardiovasc Res. 2001;50:301–313. doi: 10.1016/s0008-6363(00)00293-5. [DOI] [PubMed] [Google Scholar]
- 45.Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400:566–569. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- 46.Clancy CE, Zhu ZI, Rudy Y. Pharmacogenetics and anti-arrhythmic drug therapy: a theoretical investigation. Am J Physiol Heart Circ Physiol. 2007;292:H66–H75. doi: 10.1152/ajpheart.00312.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Niggli E, Lederer WJ. Voltage-independent calcium release in heart muscle. Science. 1990;250:565–568. doi: 10.1126/science.2173135. [DOI] [PubMed] [Google Scholar]