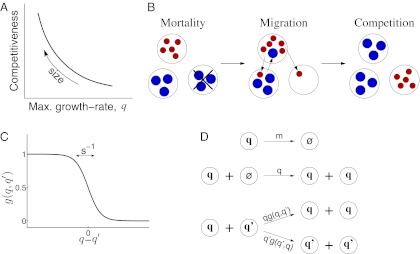
Fig. 1.
Stochastic colonization-competition model. (A) Body size is associated with a tradeoff between maximal growth rate, q, and competitiveness abilities such as direct interference. (B) Schematic illustration of the dynamic processes. Mortality (or path destruction and creation): occupied patches are emptied at a rate m. Migration: each species spreads migrants from its home patch to random patches at a rate proportional to its maximal growth rate q. Competition: if the destination patch is empty, the migrant invades; if the patch is already occupied by a 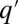 -species, the q-migrant takes over with a probability
-species, the q-migrant takes over with a probability 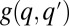 and is being eliminated otherwise. (C) The invasion probability
and is being eliminated otherwise. (C) The invasion probability 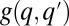 has a sigmoidal shape with a width ∼
has a sigmoidal shape with a width ∼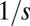 , which corresponds to stochasticity. Species with higher q have a smaller chance of taking over occupied patches. (D) Competition is much faster than migration, which implies that each patch is either empty (
, which corresponds to stochasticity. Species with higher q have a smaller chance of taking over occupied patches. (D) Competition is much faster than migration, which implies that each patch is either empty ( ) or occupied by a single species, entitled by its maximal growth rate (q). The resulting dynamics are that of a well-mixed population of patches subject to the illustrated rate equations for all q and
) or occupied by a single species, entitled by its maximal growth rate (q). The resulting dynamics are that of a well-mixed population of patches subject to the illustrated rate equations for all q and 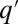 : exchange (up), colonization of empty patches (middle), and invasion into occupied patches (down). The corresponding mean-field equation is Eq. 2.
: exchange (up), colonization of empty patches (middle), and invasion into occupied patches (down). The corresponding mean-field equation is Eq. 2.