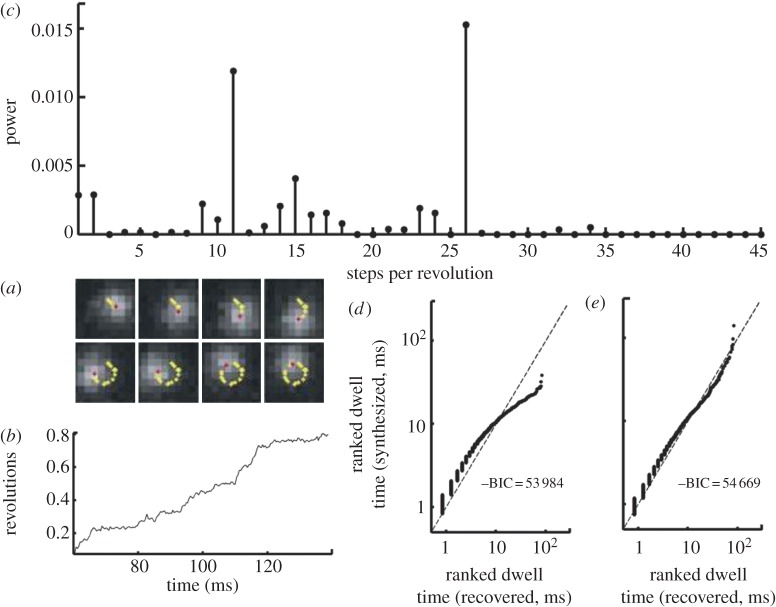
Figure 2.

Extracting discrete states and dwell time distributions of the bacterial flagellar motor. (a) Sequence of EMCCD frames of a bead attached to a bacterial flagellar hook, the estimated centre of the bead over time shown in the yellow, time–position trace. (b) Time–angle signal estimated from the time–position trace in (a). (c) Square magnitude of ECF components averaged over step-smoothed time–position traces, showing the dominant 26-fold periodicity and strong evidence for 11-fold periodicity. This periodicity is related to the number of motor proteins. Horizontal axis is frequency in steps per revolution (d) Estimated dwell times against samples from an exponential model which assumes Poisson motor stepping, and (e) the same estimated dwell times against samples from a power-law model—(d) and (e) show quantile–quantile plots: a perfect model will have all points lying on the dotted diagonal line, and the closer the points to that line, the better the model for the dwell times. The power-law model is visually a much better fit, but additionally the Bayesian information criterion (BIC) that quantifies the quality of the fit is larger for the power-law model, confirming the visual conclusion that the motor stepping is non-Poisson. (Online version in colour.)