Figure 1.
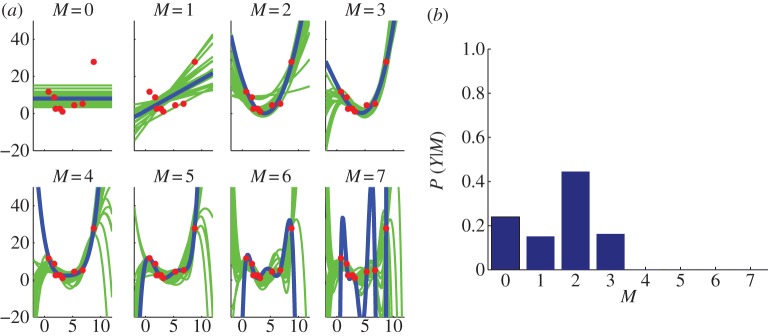
Marginal likelihoods, Occam’s razor and overfitting: consider modelling a function y=f(x)+ϵ describing the relationship between some input variable x, and some output or response variable y. (a) The red dots in the plots on the left-hand side are a dataset of eight (x,y) pairs of points. There are many possible f that could model this given data. Let us consider polynomials of different order, ranging from constant (M=0), linear (M=1), quadratic (M=2), etc., to seventh order (M=7). The blue curves depict maximum-likelihood polynomials fit to the data under Gaussian noise assumptions (i.e. least-squares fits). Clearly, the M=7 polynomial can fit the data perfectly, but it seems to be overfitting wildly, predicting that the function will shoot off up or down between neighbouring observed data points. By contrast, the constant polynomial may be underfitting, in the sense that it might not pick up some of the structure in the data. The green curves indicate 20 random samples from the Bayesian posterior of polynomials of different order given this data. A Gaussian prior was used for the coefficients, and an inverse gamma prior on the noise variance (these conjugate choices mean that the posterior can be analytically integrated). The samples show that there is considerable posterior uncertainty given the data, and also that the maximum-likelihood estimate can be very different from the typical sample from the posterior. (b) The normalized model evidence or marginal likelihood for this model is plotted as a function of the model order, P(Y |M), where the dataset Y are the eight observed output y values. Note that given the data, model orders ranging from M=0 to M=3 have considerably higher marginal likelihood than other model orders, which seems plausible given the data. Higher-order models, M>3, have relatively much smaller marginal likelihood, which is not visible on this scale. The decrease in marginal likelihood as a function of model order is a reflection of the automatic Occam razor that results from Bayesian marginalization.