Figure 5.

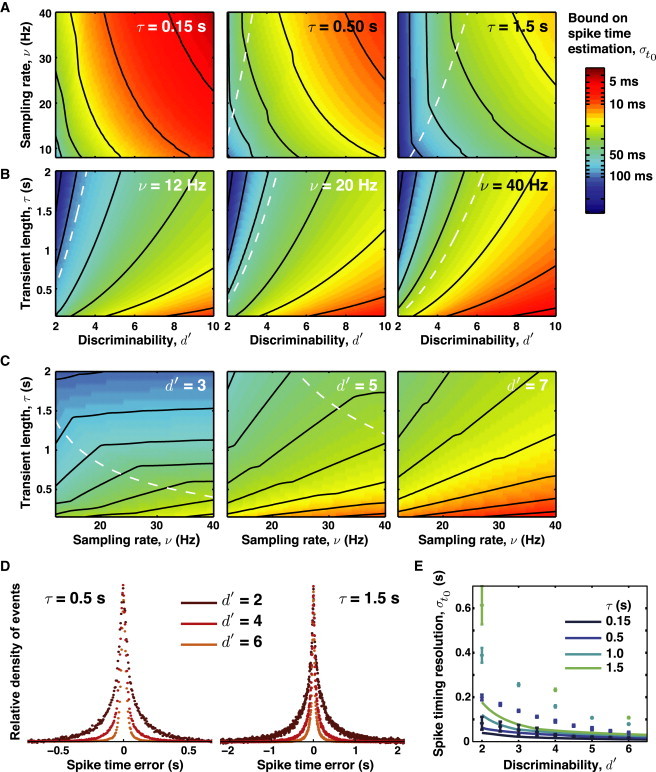
Chapman-Robbins lower bounds on the estimation of spike times. The ability to accurately estimate a spike’s time is governed by the discriminability, d′, the sampling rate, ν, and the duration of the signal transient, τ. For fixed d′, spike timing precision improves with shorter optical transients and higher sampling rates. The Chapman-Robbins lower bound can be either lower or higher than the sampling rate and exhibits strong dependence on discriminability d′ and transient duration. (A) Comparison of three optical indicators with different decay kinetics. A fast optical indicator (τ ∼ 0.15 s) such as Oregon Green BAPTA-1 (OGB-1) can localize spikes to ∼30 ms, even in regimes with modest SNR regimes (d′ ∼ 3). Slower indicators with time constants resembling those of GCaMP3 (∼0.5 s) exhibit poorer spike timing characteristics. In regimes with modest SNR, even slower indicators with kinetics resembling those of d3cpv or TN-XXL (1.5 s) allow spike localization with ∼100 ms resolution. (B) Comparison of estimation bounds at three different sampling rates. Increasing the sampling rate modestly improves spike timing resolution. (C) Increasing discriminability also significantly improves spike timing resolution. (A–C, white dashed line) Boundary of the regime of temporal super-resolution. (D) Simulations of spike timing resolution. Using a brute-force maximum likelihood method for determining the spike time, we obtained histograms of the spike time error for two indicators with distinct temporal dynamics. Note the different time scales on the two panels. For visual clarity, histograms are shown normalized to a common peak value. (E) Plots of simulated spike timing resolution and the theoretically calculated Chapman-Robbins lower bound. The simulations generally do not attain the Chapman-Robbins lower bound, especially for situations with low SNR and slow temporal dynamics. Simulations in panels D and E were done using ν = 20 Hz.