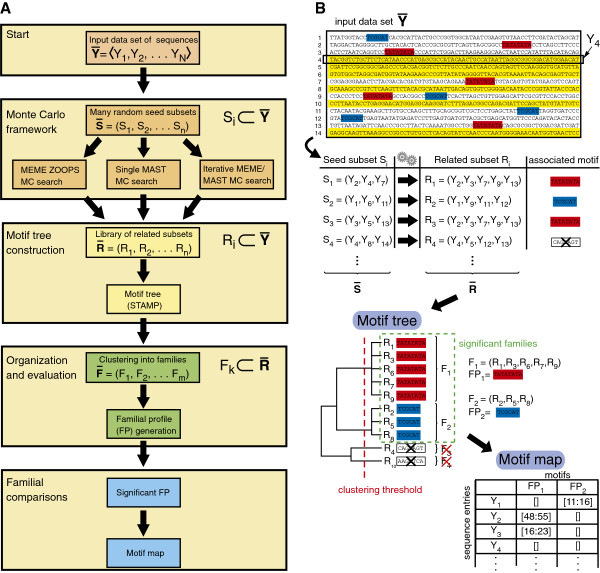
Figure 2.

Flowchart of the MotifCatcher algorithm. (A) The MotifCatcher pipeline may be conceptually divided into 4 processing stages, starting with an input data set of sequences $\overline{Y}$: (1) A set of random subsets of $\overline{Y},\overline{S}=\left(S_1,S_2,\dots S_n\right)$, where each $S_i\subset \overline{Y}$, are converted into a set of related subsets $\overline{R}=\left(R_1,R_2,\dots R_n\right)$, using one of the three related subset determination protocols. (2) $R_i\subset \overline{R}$ (with statistically significant associated motifs) are organized into a branching diagram according to the similarity of their motifs using the STAMP platform. (3) R_i with highly similar associated motifs are clustered together into families F_i according to a user-determined clustering threshold. (4) A representative motif of each family, the familiar profile (FP), is computed, as well as a motif map of the subsequences from all sequence entries from $\overline{Y}$ used to construct different FPs. (B) Application of the MotifCatcher algorithm to a toy data set of 14 sequence entries, all 68 nt in length. Two significant motifs (TATATATA, highlighted in red, and CTGCAT, highlighted in blue) are recovered from a MotifCatcher search of 10 seeds. In this example, 6 of the 14 sequence entries do not contain a significant motif (highlighted in yellow). 8 of the 10 seeds converge to a meaningful motif (three examples illustrated in random subsets S₁, S₂, and S₃), and 2 of the 10 seeds do not (exemplified in random subset S₄). Seed subsets containing motif-rich sequence entries converge to related subsets with meaningful motifs, seed subsets lacking motif-rich sequence entries do not converge to related subsets with meaningful motifs (and so are discarded). Conversion of a seed subset S_i to a related subset R_i is achieved by one of three different protocols, here represented by gears, and arrows pointing from each enumerated seed subset to its resultant related subset. The 10 related subsets are organized into a motif tree, thereupon the 2 related subsets lacking meaningful motifs are discarded, and familial profiles are determined for the 2 meaningful families. A motif map structure maps familial profiles back to the input data set $\overline{Y}$.