Fig. 1.

Successive shapes formed by plant organs undergoing gravitropism and a geometrical description of these shapes. (A) Time-lapse photographs of the gravitropic response of a wheat coleoptile placed horizontally (Movie S1). (B) Time-lapse photographs of the gravitropic response of an Arabidopsis inflorescence placed horizontally (Movie S2). White bars, 1 cm. (C) Geometric description of organ shape. The median line of an organ of total length L is in a plane defined by coordinates x, y. The arc length s is defined along the median line, with s = 0 referring to the base and s = L referring to the apex. In an elongating organ, only the part inside the growth zone of length L_gz from the apex is able to curve (with 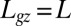at early stages and 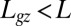later on), whereas the whole length is able to curve in organs undergoing secondary growth (i.e., 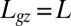). 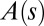is the local orientation of the organ with respect to the vertical and 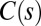the local curvature. The two curves shown have the same apical angle 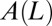but different shapes, so to specify the shape we need the form of 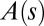or 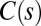along the entire median. Due to the symmetry of the system around the vertical axis, the angle A is a zenith angle—that is, it is zero when the organ is vertical and upright. Thus, an orthotropic organ has a gravitropic set point angle of 0. For simplicity, clockwise angles are considered as positive.