Fig 3.

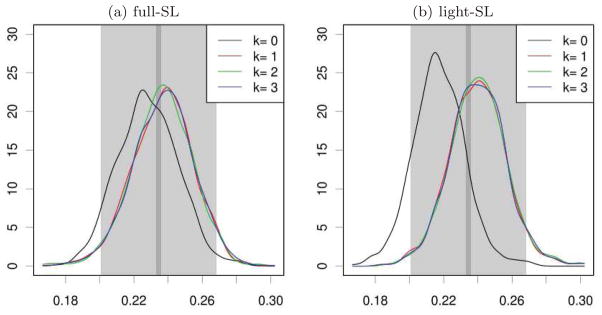
Empirical distribution of { ${\mathrm{\Psi }}_{n,b}^k:b\le B^{\prime }$} based on n = 200 independent observed data structures for k = 0 (initial estimator) and k iterations of the updating procedure (k = 1, 2, 3), as obtained from B′ = 10³ independent replications of the simulation study (using a Gaussian kernel density estimator). (a). The super-learning procedure involves all algorithms described in Section 6.5. (b). The super-learning procedure only involves algorithms based on generalized linear models. In both graphics, gray rectangles represent 95%-accuracy intervals $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}]$ and $[{\psi }_B(P^{(s)})\pm {\xi }_{0.975}\sqrt{v_B(P^s)/B}]$ for the true parameter Ψ (P^s) based on 200 observed data structures (light gray) and B = 10⁵ observed data structures (dark p gray). The length of $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}]$ is the optimal length of a 95%-confidence interval based on an efficient (regular) estimator of Ψ (P^s) relying on n observations (assuming that the asymptotic regime is reached).