Abstract
This paper presents marginal structural models (MSMs) with inverse propensity weighting (IPW) for assessing mediation. Generally, individuals are not randomly assigned to levels of the mediator. Therefore, confounders of the mediator and outcome may exist that limit causal inferences, a goal of mediation analysis. Either regression adjustment or IPW can be used to take confounding into account, but IPW has several advantages. Regression adjustment of even one confounder of the mediator and outcome that has been influenced by treatment results in biased estimates of the direct effect (i.e., the effect of treatment on the outcome that does not go through the mediator). One advantage of IPW is that it can properly adjust for this type of confounding, assuming there are no unmeasured confounders. Further, we illustrate that IPW estimation provides unbiased estimates of all effects when there is a baseline moderator variable that interacts with the treatment, when there is a baseline moderator variable that interacts with the mediator, and when the treatment interacts with the mediator. IPW estimation also provides unbiased estimates of all effects in the presence of non-randomized treatments. In addition, for testing mediation we propose a test of the null hypothesis of no mediation. Finally, we illustrate this approach with an empirical data set in which the mediator is continuous, as is often the case in psychological research.
Conceptually, mediation occurs as part of a hypothesized causal chain of events: the independent variable (e.g., job search intervention) has an effect on a mediator (e.g., job-search self-efficacy), which then affects the dependent variable (e.g., depressive symptoms). For example, knowledge of health consequences, attitudes, social norms, availability, and refusal skills have been hypothesized to mediate the effect of prevention interventions on adolescent smoking (MacKinnon, Taborga, & Morgan-Lopez, 2002). Sometimes individuals are randomly assigned to the treatment intervention and other times, they are not. Regardless, individuals are typically not randomized to levels of the mediator.
A simple mediation model is one in which an intervention, denoted T for treatment, causes a change in the mediator, denoted M, which in turn causes a change in the dependent variable, denoted Y. Because T is hypothesized to cause a change in M, we assume throughout this manuscript that T occurs before M. Similarly, because M is hypothesized to cause a change in Y, we assume throughout that M occurs before Y. Mediation analysis is, by definition, a question about causal pathways and causal inference (MacKinnon, 2008). If individuals are randomly assigned to levels of T, then a causal inference regarding the effect of T on M is straightforward to assess because proper randomization reduces the likelihood that there are confounders that influence both T and M. Intuitively, confounders of the effect of T on M are variables that directly affect both the hypothesized cause, in this case T, and the outcome, in this case M, potentially biasing the estimate of a causal effect. Regardless of randomization to T, individuals cannot typically be randomized to levels of M because M is an outcome of T. Thus, causal inference regarding the effect of M on Y is not straightforward to assess because there may be other variables in addition to T (i.e., confounders) that influence both M, the hypothesized cause in this case, and Y, the outcome in this case.
Throughout this manuscript, we use the term confounder to refer to extraneous variables that are common causes of the hypothesized causal variable and the outcome. If these variables are not taken into account, either through randomization or by statistical means, then they may result in a spurious relationship between the hypothesized cause and the outcome. That is, the researcher may erroneously conclude that there is a causal relationship between the hypothesized causal variable and the outcome. Note that if a variable is related only to an outcome and not the hypothesized cause, it will not bias the estimated causal effect but it may introduce noise into the estimate. We do not consider these variables to be confounders. Throughout the manuscript, we will assume that these confounders are measured and can, by some means, be adjusted for (as will be described in greater detail below). If this is not the case, then other assumptions may be needed in order to estimate causal effects or causal inference may not be possible. Throughout the manuscript, we will refer to a confounder of M and Y that has itself been influenced by T as a post-treatment confounder and denote it X1. We will refer to a confounder that occurs prior to T (and therefore, could not itself have been influenced by T) as a pre-treatment confounder and denote it X0.
We begin with a review of direct and indirect effects that have been defined using the potential outcomes framework in the statistical and epidemiology literature and the assumptions needed for identifying these effects. As VanderWeele and Vansteelandt (2009) pointed out, it is not possible to identify a causal estimand of the indirect effect itself in the presence of both a treatment-mediator interaction and a post-treatment confounder. Our proposed approach will be based on the potential outcomes framework (Holland, 1986; Rubin, 1974, 2005) and marginal structural models (MSMs; Robins, Hernan, & Brumback, 2000). It should be noted that we are not the first to propose using MSMs in the context of mediation (see VanderWeele, 2009) nor are we the first to propose the potential outcomes framework more generally for assessing mediation (see, e.g., Albert, 2007; Emsley, Dunn, & White, 2010; Imai, Keele, & Tingley, 2010; Jo, 2008; Pearl, 2001; Robins & Greenland, 1992; Rubin, 2004; Sobel, 2008). However, MSMs have been used much less in the social sciences than they have been in epidemiology. Thus, below we will review the potential outcomes framework and MSMs.
With this background, we will proceed to argue that although the indirect effect can not be identified in the presence of both an interaction and post-treatment confounders, the individual effects involved in the mediation process are scientifically interesting, important, and are identified. We will define the causal effect of T on M and refer to this as Effect 1 and we will define the causal effect of M on Y, given treatment history (i.e., T) and refer to this as Effect 2 throughout. We will refer to the effect of T on Y, conditional on M as the direct effect. Next, in the presence of an interaction between T and M; a post-treatment confounder; a baseline (i.e., pre-treatment) moderator, denoted Z; and non-randomized T, we will describe an approach for assessing mediation using MSMs and inverse propensity weighting (IPW; Robins, Rotnitzky, & Zhao, 1995) to estimate Effects 1, 2, and the direct effect. We will then test the null hypothesis that either or both of Effects 1 and 2 are zero and examine the power of this test using a simulation study. Finally, we will illustrate through an empirical example how the proposed approach can be implemented. The proposed approach is not that different from the approach currently taken by social/behavioral scientists, although it does have several advantages and disadvantages which will be presented after the approach has been described.
The Potential Outcomes Framework
Non-mediation context
Since the potential outcomes framework has only recently been introduced in the social science methodology literature, we will briefly review the potential outcomes framework for the simplest case: for estimating the causal effect of a binary T on Y. In the next section, we will introduce a mediating variable.
In the potential outcomes framework (Rubin, 1974, 2005), also known as the counterfactual framework (Morgan & Winship, 2007) or Rubin’s causal model (Holland, 1986), each individual has a potential outcome for each possible treatment condition. In the simplest case, one treatment group and one control group, there are two potential outcomes for each participant: the outcome that would be obtained under the treatment condition and the outcome that would be obtained under the control condition. Let Ti denote the treatment received by participant i, i = 1, …, N. Those with Ti = 1 are said to be treated, and those with Ti = 0 are said to be untreated. Let Yi(0) be the outcome if Ti = 0, and Yi(1) be the outcome if Ti = 1. The individual causal effect is defined as the difference between these two potential outcomes for participant i, Yi(1) – Yi(0). Because each participant can be observed in only one of these conditions, in every case one of the potential outcomes is missing (e.g., Yi(1) is missing when Ti = 0). Therefore, the individual causal effect can not be computed directly. However, various strategies have been proposed to estimate the average causal effect (ACE), the causal effect averaged over participants in the study defined as E(Yi(1) – Yi(0)). More detailed introductions to the potential outcomes framework outside of the context of mediation are provided by Little and Rubin (2000); Schafer and Kang (2008); West, Biesanz, and Pitts (2000); and Winship and Morgan (1999).
Mediation context
When a mediator is involved, the process of applying the potential outcomes framework becomes more complicated. There are now potential outcomes for both the mediator and the dependent variable, Y, because the mediator itself is an outcome of the treatment. Hence, there are missing values for both the mediator and the dependent variable because the mediator is re-expressed as a set of potential outcomes Mi(1), Mi(0) corresponding to Ti = 1, Ti = 0. The dependent variable then becomes a function of both the treatment received and the mediator (i.e., Yi(1, M(1)), Yi(0, M(0)). Thus, for individuals in the control condition, the potential outcomes for the mediator, Mi(1), and the dependent variable, Yi(1, M(1)), under treatment are missing. Likewise, for individuals who receive the treatment, the potential outcomes for the mediator, Mi(0), and the dependent variable, Yi(0, M(0)), are missing.
The above notation for the potential outcomes framework assumes that there is no interference among individuals because the potential outcomes are written as a function of Ti and not Tj, where i and j denote two different individuals. That is, one individual’s outcome does not depend on another individual’s treatment assignment. Thus, a nested or multilevel data structure may violate this assumption. Methods have recently appeared in the statistics literature for violations of this assumption (see, e.g., Hong & Raudenbush, 2005, 2006; Hudgens & Halloran, 2008; Sobel, 2006; VanderWeele, 2008, 2010) but we make this no-interference assumption throughout this article.
The notation as defined above also assumes treatment-variation irrelevance (VanderWeele & Vansteelandt, 2009). It means that the potential outcomes, Mi(t), for individual i when exposed to treatment Ti = t will be the same no matter what mechanism is used to assign treatment t to individual i. Similarly, the potential outcomes, Yi(t, m), for individual i when exposed to treatment Ti = t and mediator level Mi = m will be the same no matter what mechanism is used to assign t and m to individual i.
Finally, it is assumed that the observed mediator value for individual i, Mi, is Mi(t), when Ti = t. Likewise, it is assumed the observed outcome for individual i, Yi, is Yi(t, m) when Ti = t and Mi = m. This assumption is usually referred to as consistency and is described in greater detail in, for example, VanderWeele and Vansteelandt (2009). For the remainder of this article, we will drop the i subscript for simplicity.
Definitions of Mediation
Traditional social science approach
The literature on statistical mediation analysis (MacKinnon, 2008) often denotes the effect of T on M as a, the effect of M on Y holding constant (i.e., conditional on) T as b, and the effect of T on Y holding constant M as c′. This latter effect is referred to as the direct effect. It is the effect of T on Y that does not go through M. In the social science literature, the indirect or mediated effect of T on Y is often defined as ab, the product of a and b, and the total effect of T on Y is defined as ab + c′. Thus, the indirect effect could also be defined as the total effect minus the direct effect. Note that these definitions are entangled with particular model assumptions such as linearity and additivity (i.e., no interactions) that are often not clearly stated. Mediation analysis is then performed by fitting two regression models separately or simultaneously using structural equation modeling (SEM) software. We will refer to this approach whether fitting the regression models separately or simultaneously as the traditional social science approach.
Potential outcomes framework
Using the potential outcomes framework, direct and indirect effects can be defined without particular model assumptions. However, within the potential outcomes framework, there are different definitions of direct and indirect effects. For example, some researchers (e.g., Jo, 2008; Sobel, 2008; Albert, 2007) have defined mediation within the potential outcomes framework using principal stratification (Frangakis & Rubin, 2002; Frangakis, 2004) and instrumental variables (Angrist, Imbens, & Rubin, 1996). Jo (2008) has shown that under fairly stringent assumptions (e.g., no interactions between T and M, no direct effect of T on Y, and no iatrogenic effects of T on M), principal strata effects coincide with the traditional social science indirect effect. We will not pursue the principal strata definition but interested readers may consult Rubin (2004), Gallop et al. (2009), Jo (2008), Elliott, Raghunathan, and Li (2010), VanderWeele (2008), and Ghosh, Elliott, and Taylor (2010) for details on using principal stratification to assess mediation.
Other attempts to define mediation within the potential outcomes framework have resulted in definitions termed pure effects (Holland, 1988; Robins & Greenland, 1992) and controlled effects (Robins & Greenland, 1992). Pure effects were later referred to as natural effects by Pearl (2001); this term has often been used by others (e.g., Imai, Keele, & Tingley, 2010; VanderWeele, 2009) and we will use it as well. VanderWeele (2009) gives definitions of these effects and the conditions under which they are generally identified. Here, we provide a summary of this work for those readers not familiar with it. Table 1 presents each of the types of effects in expectation notation. We begin by discussing direct effects (i.e., the effect of T on Y that does not go through M).
Table 1.
Summary of Definitions of Direct and Indirect Effects
| Effect | Mathematical | Conceptual |
|---|---|---|
| Direct Effects | ||
| Controlled | E[Y(t, m) − Y(t′, m)] | Causal effect on Y of changing from T = t to T = t′ when M = m. |
| Natural | E[Y(t, M(t′)) − Y(t′, M(t′))] | Causal effect on Y of changing from T = t to T = t′ when M is set to what it would have been under T = t′ |
| E[Y(t, M(t)) − Y(t′, M(t))] | Causal effect on Y of changing from T = t to T = t′ when M is set to what it would have been under T = t |
|
| Indirect Effects | ||
| Natural | E[Y(t′, M(t)) − Y(t′, M(t′))] | Causal effect on Y of the difference in the level of the mediator that would be obtained under T = t versus the level of the mediator that would be obtained under T = t′ for T = t′ |
| E[Y(t, M(t)) − Y(t, M(t′))] | Causal effect on Y of the difference in the level of the mediator that would be obtained under T = t versus the level of the mediator that would be obtained under T = t′ for T = t. |
Controlled direct effect
The controlled direct effect sets M to some specific value, m, for the entire population and expresses the causal effect on Y of changing from the treatment to control group for M = m. As shown in Table 1, controlled direct effects are defined as E[Y(t, m) – Y(t′, m)] where Y(t, m) is the potential outcome when T = t and M = m. For the moment, consider the case where T and M are both binary and take on values of 1 or 0. Then the controlled direct effect of t = 1 versus t′ = 0 would be E[Y(1, m) – Y(0, m)] where m = 1 and E[Y(1, m′) – Y(0, m′)] where m′ = 0. Thus, there are two controlled direct effects: one for each level of m. There are as many controlled direct effects as there are levels of M. It is important to note that we have imposed no particular model and, therefore, no model assumptions on this definition. The direct effect as defined in the traditional social science literature, c′, imposes a “no-interactionis” assumption such that c′ does not differ across levels of M. That is, E[Y(1, m) – Y(0, m)] = E[Y(1, m′) – Y(0, m′)] for all m and m′. For a linear model, this equality holds if there is not an effect of a T × M product term. When we use the phrase no-interaction, we will mean the broader definition that all controlled direct effects are equal.
Natural direct effect
Next, consider the natural direct effect. As shown in Table 1, the natural direct effect is E[Y(t, M(t′)) – Y(t′, M(t′))]. Now, M is not set to some specific value, m, for the entire population; rather, it takes on whatever value it would have had under T = t′. In contrast to the controlled direct effect, the natural direct effect allows for natural variability in M among individuals. Hence, it is important to note the difference in notation. Lowercase m refers to a specific value of M but M(1) and M(0) refer to potential values (under treatment and control, respectively) and these values may differ across individuals. If T is binary, then there are two of these natural direct effects, E[Y(1, M(0)) – Y(0, M(0))] and E[Y(1, M(1)) – Y(0, M(1))]. The former addresses the causal effect of T on Y setting the level of the mediator to the value it would have had in the control condition. The latter addresses the causal effect of T on Y setting the level of the mediator to the value it would have had in the treatment condition. Again, these values for the mediator are not necessarily the same across individuals: for one individual, M(1) may equal m and for another M(1) may equal m′.
Natural indirect effect
Next, consider the natural indirect effect, defined as E[Y(t, M(t)) – Y(t, M(t′))], which is the causal effect of the difference in the level of the mediator that would be obtained under treatment versus the level of the mediator that would be obtained under the control for T = t. Note that if T is binary, again there are two of these, one for T = t and one for T = t′. Natural direct and indirect effects are appealing because the total effect, defined as E[Y(t, M(t)) – Y(t′, M(t′))], can be decomposed into the natural direct and indirect effects (see, e.g., Imai, Keele, & Yamamoto, 2010; Pearl, 2010a, 2010b; VanderWeele, 2009) just as the traditional social science total effect, denoted c, can be decomposed into ab + c′. In contrast, for controlled effects, the total effect cannot necessarily be decomposed in this manner. There is not a controlled indirect effect that is comparable to the natural indirect effect without further assumptions.
Assumptions Needed to Identify Effects
Recall that the causal effects are defined for individuals but we do not observe all the potential outcomes for an individual. Therefore, the estimands defined above cannot be estimated from the observed data without identifying assumptions. VanderWeele (2009); Imai, Keele, and Tingley (2010); and Imai, Keele, and Yamamoto (2010) give assumptions generally needed to identify the natural effects defined above. By identify, we mean that the effects can be consistently estimated from the observed data. These assumptions are summarized in Table 2. Assumption A is that there are no unmeasured confounders of T and Y. That is, T ⊥ Y(t, m)|X0. Assumption B is that there are no unmeasured confounders of M and Y. That is, M ⊥ Y(t, m)|T, X0, X1. Assumption C is that there are no unmeasured confounders of T and M. That is, T ⊥ M(t)|X0. Finally, one of two assumptions needs to be made. We will discuss the first one (D1) here and the second one (D2) below. Assumption D1 is that there are no confounders of M and Y that may have been influenced by T (i.e., post-treatment confounders; see, e.g., Avin, Shipster, & Pearl, 2005; Imai, Keele, & Tingley, 2010; Imai, Keele, & Yamamoto, 2010; VanderWeele, 2009). That is, M(t) ⊥ Y(t′, m)|X0. This assumption is unrealistic in many applied contexts. For example, this assumption is violated when there are multiple mediators, because these other mediators are variables that are related to both the dependent variable and the original mediator of interest and have been influenced by the treatment. In fact, post-treatment confounders are mediators themselves, although the researcher may not be substantively interested in them (see, e.g., Greenland & Morgenstern, 2001; MacKinnon, Krull, & Lockwood, 2000); this is why we refer to them as confounders rather than mediators. The recent methods proposed by Imai, Keele, and Tingley (2010) do not allow for post-treatment confounders whether measured or not. Together, these four assumptions (A-D1) identify the natural direct and indirect effects. Other alternative identifying assumptions are also possible (Hafeman & VanderWeele, 2010) but generally Assumptions A-D1 are used.
Table 2.
Summary of Assumptions for Identifying Direct and Indirect Effects
| Assumption | Mathematical | Conceptual |
|---|---|---|
| A. | T ⊥ Y(t, m)|X0 | No unmeasured confounders of T and Y. |
| B. | M ⊥ Y(t, m)|T, X0, X1 | No unmeasured confounders of M and Y. |
| C. | T ⊥ M(t)|X0 | No unmeasured confounders of T and M. |
| D1. | M(t) ⊥ Y(t′, m)|X0 | No measured or unmeasured confounders of M and Y that have been influenced by T. |
| D2. |
E[Y(1, m) − Y(0, m)] = E[Y(1, m′) − Y(0, m′)] for all m and m′ |
No interaction between T and M. |
Assumptions A-D1 are needed to identify natural effects but only Assumptions A and B are needed for identifying controlled direct effects. However, identifying the controlled direct effect does not identify the indirect effect, in which social scientists are most interested, unless we assume (D2) that there are no interactions between T and M (i.e., the controlled direct effects are equal across all levels of the mediator). If there is no interaction, then the controlled direct effect equals the natural direct effect. Then, using the decomposition of natural effects, the indirect effect can be obtained by subtracting the controlled direct effect from the total effect (VanderWeele, 2009). However, many substantive questions involve interactions, often referred to as moderated mediation and mediated moderation (see, e.g., Edwards & Lambert, 2007; MacKinnon, 2008; Muller, Judd, & Yzerbyt, 2005; Preacher, Rucker, & Hayes, 2007). Even if researchers have not asked substantive questions about interactions, they nevertheless may exist. Therefore, researchers may not want to make Assumption D2.
To estimate the indirect effect via the estimation of controlled direct effects, identifying Assumptions A, B, and D2 from Table 2 are needed. If individuals are randomly assigned to T then Assumption A is satisfied. Assumption A is also satisfied even if individuals are not randomly assigned to T as long as all potential confounders of T and Y have been measured and properly adjusted for. Random assignment is often considered the gold standard because Assumption A is a strong assumption that cannot be verified in any given study. Assumption B is satisfied if individuals are randomly assigned to levels of M. However, this is usually not possible, although Assumption B is also satisfied if all potential confounders of M and Y are measured and properly adjusted for. Again, this is a strong assumption that cannot be verified in any given study. Assumption D2 is satisfied if the controlled direct effect does not vary across levels of M. In this case, the decomposition, total effect = direct effect + indirect effect, holds. Without Assumption D2, there is not a single direct effect to subtract from the total effect because the direct effect depends on the level of M.
To obtain an estimate of the indirect effect via the estimation of natural effects, identifying Assumptions A-D1 from Table 2 are needed. The conditions under which Assumptions A, B, and D1 would hold were discussed previously. Assumption C is satisfied if individuals are randomly assigned to levels of T. Assumption C is also satisfied, in the absence of randomization, if all potential confounders of T and M are measured and properly adjusted for. Again, randomization is considered the gold standard because, like Assumptions A and B, Assumption C is a strong assumption that cannot be verified in practice. We note that the traditional social science approach also makes Assumptions A–C, although they are usually not clearly stated. Also, it is important to note that careful consideration should be given to selecting the covariates that may be potential confounders and in particular, it is necessary to adjust for more than basic demographic variables, such as gender and race (Steiner, Cook, Shadish, & Clark, 2010). On the other hand, covariates that are strongly related to the hypothesized cause and weakly associated with the outcome can amplify bias of the causal effect estimate (Pearl, 2011).
In summary, researchers need to be aware that there are different definitions of mediation effects and that different assumptions are required for identifying these effects. Assumptions A–C are needed for natural effects and Assumptions A and B are needed for controlled effects. In addition, one of the following two assumptions is needed: either there are no unmeasured or measured confounders of M and Y that have been influenced by T (D1) for natural effects, or there is not an interaction between T and M (D2) for controlled effects. Given that many scientific questions involve hypotheses about interactions and/or there are likely to be post-treatment confounders, the task of identifying, and therefore estimating, indirect effects seems daunting.
Our proposed method and how it fits in
In our proposed method, we do not assume either D1 or D2. We do make Assumptions A–C, which are plausible if the researcher has measured all potential confounders of T, M, and Y or has successfully randomized individuals to T and measured all potential confounders of M and Y. Because we do not assume either D1 or D2, we cannot obtain an estimate of the indirect effect itself. However, we can obtain estimates of each of the component effects (i.e., Effects 1 and 2) involved in the indirect effect. Even though the indirect effect itself is not identified, we can still test the null hypothesis of no mediation. Estimates of these effects and the test may suffice for some research purposes. For example, MacKinnon, Taborga, and Morgan-Lopez (2002) and MacKinnon (2008) describe the importance of examining Effects 1 and 2. They argue that if T does not causally affect M, then this suggests that the treatment should be modified so that it does causally affect M. MacKinnon, Taborga, and Morgan-Lopez (2002) and MacKinnon (2008) refer to this as action theory. They also argue that if M does not causally affect Y then no matter how well T causes a change in M, M will not cause a corresponding change in Y. In this case, they argue that the intervention should be modified to influence a different mediator, one that is more likely to be causally related to Y. MacKinnon, Taborga, and Morgan-Lopez (2002) and MacKinnon (2008) refer to this as conceptual theory. Thus, the researcher does not need an estimate of the indirect effect itself in order to test action and conceptual theories. In fact, from an indirect effect estimate that is not statistically significant, a researcher cannot determine whether there was a problem with the action theory or the conceptual theory.
With Assumptions A and B, we can identify the controlled direct effect. We will use MSMs to define the causal effects of interest in terms of the potential outcomes framework. We will then use IPW estimation to estimate the causal effects. Finally, we will describe how to test the null hypothesis that either or both of Effects 1 and 2 are zero. First, we review MSMs and IPW estimation.
Marginal Structural Models
MSMs, in the non-mediation context, have been used to define causal effects primarily in epidemiology (e.g., Bodnar, Davidian, Siega-Riz, & Tsiatis, 2004; Cole, Hernan, Anastos, Jamieson, & Robins, 2007; Ko, Hogan, & Mayer, 2003; Mortimer, Heugebauer, van der Laan, & Tager, 2005) although there are a few applications in drug prevention research (Bray, Almirall, Zimmerman, Lynam, & Murphy, 2006; L. Li, Evans, & Hser, 2010), sociology (Barber, Murphy, & Verbitsky, 2004; Wimer, Sampson, & Laub, 2008), and psychology (VanderWeele, Hawkley, Thisted, & Cacioppo, 2011). An MSM can be specified for continuous, binary, or survival outcomes. MSMs have been used primarily to define the causal effect of treatment sequences. Here we specify MSMs for mediation by treating the intervention-mediator sequence as a treatment sequence.
MSMs differ from, for example, linear regression models because they are models for potential outcomes. In contrast, a linear regression model is a model for the observed outcomes. An advantage of MSMs is that they may be used to define the causal effects of interest. To illustrate, we will use MSMs to define several causal effects that may be of interest to researchers assessing mediation. Specifically, consider defining the effect of a binary T on a continuous M (denoted a in the traditional social science approach) and the effect of a continuous M on a continuous Y for each level of T (denoted b in the traditional social science approach). To define these effects, two MSMs are needed
| (1) |
and
| (2) |
Using the model given in Equation 1,
| (3) |
defines the effect of a binary T on a continuous M. Using the model given in Equation 2,
| (4) |
defines the causal effect of M on a continuous Y for t = 1 and
| (5) |
defines the causal effect of M on a continuous Y for t = 0. A reference should be chosen for m′. The causal effect of a one-unit increase in M from the reference m′ on Y for t = 1 is (β2 + β4) and the causal effect of a one-unit increase in M from the reference m′ on Y for t = 0 is β2.
If the researcher wishes to assess mediated moderation or moderated mediation, conditional causal effects may be similarly defined. For example, consider the interaction between a moderator variable (e.g., gender), denoted Z, and T, and consider defining the causal effect of T on a continuous M conditional on Z and the causal effect of M on a continuous Y at each level of T. To define these effects, two MSMs are needed
| (6) |
and
| (7) |
Using the model given in Equation 6,
| (8) |
defines the causal effect of T on M conditional on Z. Using the model given in Equation 7,
| (9) |
defines the causal effect of M on Y for t = 1 and
| (10) |
defines the causal effect of M on Y for t = 0. Other causal estimands may be similarly defined.
Thus, MSMs allow the researcher to clarify the causal question of interest and define the causal effects in terms of potential outcomes. Note that MSMs are not necessarily linear regression models. We used linear regression models to show that, other than modeling potential outcomes, specifying MSMs is not that different from the traditional social science approach that many readers are familiar with. The advantage is that the causal effects of interest are more clearly defined using MSMs. Recall, the causal effects are defined for an individual as a contrast between two potential outcomes. The reason these models are called marginal is because they model the marginal distribution of the potential outcomes (Robins et al., 2000). Thus, they do not model the correlation between the counterfactuals. This correlation is not observed for any individual.
Estimation
Causal effects defined by MSMs are typically estimated using IPW, although other estimators are available (see, e.g., van der Wal, Prins, Lumbreras, & Geskus, 2009). IPW uses propensity scores; therefore, we will describe propensity scores and then the creation of the weights. Finally, we will discuss issues that arise when implementing IPW.
Propensity scores
Let X0 denote a vector of measured pre-treatment variables or potential confounders that may influence the probabilities of T = 1 and T = 0 in any setting other than a completely randomized experiment. Rosenbaum and Rubin (1983) defined the propensity score, denoted π, as the probability that an individual receives the treatment given these measured confounders, π = P(T = 1|X0). Propensity scores balance confounders in the following sense: in any subset of the population in which the propensity scores are constant, treated and untreated participants have identical distributions for X0. The balancing property of the propensity score has led to many propensity-based techniques for estimating causal effects, including matching (Rosenbaum & Rubin, 1985), subclassification (Rosenbaum & Rubin, 1984) and IPW (Robins et al., 1995). We will focus on estimating the causal effects using IPW. As in any method involving propensity scores, use of IPW assumes that all confounders are measured and included in the model for estimating π. Estimates of π are denoted π̂. They are obtained, for example, as the predicted probabilities from a logistic or probit regression of T on X0, but more flexible alternatives, including generalized boosted regression (McCaffrey, Ridgeway, & Morral, 2004), or classification trees (Luellen, Shadish, & Clark, 2005) have also been used.
Ideally, the distribution of the propensity scores in the treated and control conditions should overlap. With less overlap, estimates of the causal effect will have a larger variance. When there is no overlap, it means that there are essentially no individuals in the two conditions that are comparable on the potential confounders and causal inferences may not be warranted. Next, we describe how weights are created for a non-randomized binary T and then we describe how weights are created for a continuous M.
Creating the weights for a non-randomized binary treatment
The IPW estimator is similar to the Horvitz-Thompson survey sampling weighted estimator (Horvitz & Thompson, 1952), in which the weights are the inverse probability of being sampled.Robins et al. (2000) extended the idea to non-randomized time-varying treatments. Here, participants in the treatment group are given a weight of 1/P[T = 1|X0] and participants in the control group are given a weight of 1/(1 − P[T = 1|X0]). In other words, the weights correspond to the inverse of the probability of receiving the level of the treatment that the individual actually received conditional on the past potential confounders included in the propensity model. Just as survey weights adjust the sample to represent a population, inverse propensity weights adjust the sample to represent a randomized trial. IPW requires that the probabilities in the denominator of the weights are greater than zero. In other words, that each individual has some chance of receiving each treatment condition.
If there is a baseline moderator, Z, weights are usually stabilized, which helps to reduce the variability of the weights. For those in the treatment group, the model for the numerator of the weights is P[T = 1|Z] and the model for the denominator of the weights is P[T = 1|Z, X0]. Thus, the weights are P[T = 1|Z]/P[T = 1|Z, X0]. For those in the control group, the numerator and denominator of the weights are 1 − P[T = 1|Z] and 1 − P[T = 1|Z, X0], respectively. When using stabilized weights, the mean of the weights should be approximately one. For further details about creating weights and the numerator and denominator models for the weights, see Cole and Hernan (2008).
Creating the weights for a mediator
Even if assignment to levels of T is randomized, we still need to use weights to adjust for possible confounding of M and Y. We will consider the construction of weights for the following situations: binary M and no Z, continuous M and no Z, binary M and moderator Z, and continuous M and moderator Z. In all situations, the weights for M include T in both the numerator and denominator models for the weights. This is analogous to the time-varying treatment setting in which treatment history is included in both the numerator and denominator models (Robins et al., 2000). If there is no moderator Z and M is binary, then the weights for those with m = 1 are P[M = 1|T]/P[M = 1|T, X0, X1]. For those with m = 0, the weights are (1 − P[M = 1|T])/(1 − P[M = 1|T, X0, X1]). If M is continuous, as is often the case in psychological research, then the propensity score can be defined as the probability density function (p.d.f.) of the conditional distribution of the mediator given the measured confounders (Robins et al., 2000). For continuous M, the denominator model is given by a linear regression of M on X0, X1, and T and the numerator model is given by a linear regression of M on T. A denominator probability is then obtained by inserting the fitted values, m̂, in the normal p.d.f. (denoted ϕ()),
| (11) |
where σ̂ is the residual standard error from the linear regression of M on X0, X1, and T. The numerator probability is given by the p.d.f. of the conditional distribution of M on T, ϕ(M|T). The weights are then given by a ratio of the probabilities from the p.d.f.s (i.e., ϕ(M|T)/ϕ(M|T, X0, X1) as described in Robins et al. (2000).
If a moderator is of scientific interest, it would be included in both the numerator and denominator propensity models. If M is binary, then the weights for those with m = 1 are P[M = 1|T, Z]/P[M = 1|T, Z, X0, X1] and the weights for those with m = 0 are (1 − P[M = 1|T, Z])/(1 − P[M = 1|T, Z, X0, X1]). If M is continuous, then the weights are given by a ratio of the probabilities from the p.d.f.s, ϕ(M|T, Z)/ϕ(M|T, Z, X0, X1).
Implementation
Assuming no-interference, treatment-variation irrelevance, consistency, and Assumptions A–C, then the MSM for the causal effect of T on M can be written in terms of the observed data,
| (12) |
Likewise, the MSM for the causal effect on Y can be written in terms of the observed data,
| (13) |
When fitting these models to the observed data, the weights are incorporated into the models in the same manner as survey weights by using, for example, the survey package for R (Lumley, 2010). Weighting adjusts for confounding; therefore, the model needs to include only the treatment indicator variable, the mediator variable, the moderator variable (if there is one), and any interactions. If individuals are randomized to T, then the weights for M (described above) are included in the model given in Equation 13. Weights would not be needed for the model given in Equation 12 because of randomization. However, if individuals are not randomly assigned to levels of T, then weights must be included to adjust for possible confounders of T and M and/or T and Y. In this case, the weights for T (described above) are used in the model given in Equation 12. The weights used for estimating the model in Equation 13 are the product of the weights for T and M just as product weights are used in the time-varying treatment context (see Robins et al., 2000).
Testing the Mediation Effects
We will test the null hypothesis that Effect 1 or Effect 2 is zero or both are zero. To test this null hypothesis, we will test whether the product of these two effects is zero; in the traditional social science approach, the product of these two effects has been used as a definition of the indirect effect and the product of the estimates of these two effects has been used as an estimate of the indirect effect. However, here we are simply using the product as a tool for testing the null hypothesis and not as a definition of mediation. If either one of the effects or both are zero then the product will be zero. Thus, if we reject the null hypothesis, then we can conclude that both of the effects are statistically different from zero. The details of this test are given in the Appendix.
Conceptually, this null hypothesis test is similar to the Sobel (1982) test, with which readers are probably familiar. There are two important differences, though. First, the Sobel test uses the asymptotic standard error based on the normal theory covariance matrix of the estimates. Instead, we obtain an estimate of the standard error based on a covariance matrix of estimates obtained via a non-parametric bootstrap procedure. Second, because we estimate propensity scores for use in computing the weights and there is some uncertainty in this estimation, the bootstrap procedure resamples the original data prior to estimating the propensity scores. To summarize the bootstrap procedure, we resample from the original data 1000 times. For each bootstrap sample, we fit the propensity models to estimate the propensity scores, compute the weights, and estimate the causal effect using IPW. The estimate of the covariance matrix, Σ, is the variance and covariance of the estimates across the 1000 bootstrap replications. We then use this as an estimate of Σ (see Appendix). Thus, the usual Sobel test would not account for uncertainty in estimating the propensity scores. In the next section (Simulation Study: Method), we specify the null hypotheses for each interaction condition that we consider in the simulation study because the tested effects differ depending on whether there are interactions.
Summary and Rationale of the Simulation Study
We will define and estimate Effects 1 and 2, and the direct effect. To define these effects, we will use MSMs that correspond to the two regression equations currently used for assessing mediation in the traditional social science approach, but we will use IPW, rather than ordinary least squares (OLS), to estimate these effects. Our approach, unlike that of Imai, Keele, and Yamamoto (2010) and Imai, Keele, and Tingley (2010), does not require the assumption that there are no post-treatment confounders of M and Y that have been influenced by T. Our approach also allows the scientist to test action theory and conceptual theory as described by MacKinnon (2008) and MacKinnon, Taborga, and Morgan-Lopez (2002). Even though we do not identify the indirect effect itself, we do provide a test based on the two component effects (i.e., Effects 1 & 2) of mediation. In addition, if there are no interactions, then our approach allows estimation of the indirect effect by estimating the controlled direct effect and subtracting it from the total effect of T on Y. The assumption regarding no interactions can be tested.
Next, using a simulation study, we will compare bias in the estimates obtained from IPW, an OLS regression adjustment for confounding, and an OLS unadjusted regression estimate. We include the unadjusted estimate for two reasons: first, it provides a baseline; second, this is, unfortunately, the model that applied researchers often use when assessing mediation. We also assess the power of the test for mediation.
The purpose of the simulation study is twofold. The primary purpose is to assess the power of the test. The secondary purpose is to illustrate the analytical result that conditioning on even one post-treatment confounder results in bias of the direct effect. Yet, not including the post-treatment confounder in the regression results in bias of Effect 2. However, IPW provides unbiased estimates of both Effect 2 and the direct effect. This result was proven analytically byRobins et al. (2000) and is well-known in the epidemiology literature but is much less well-known in the social and behavioral sciences.
Simulation Study: Method
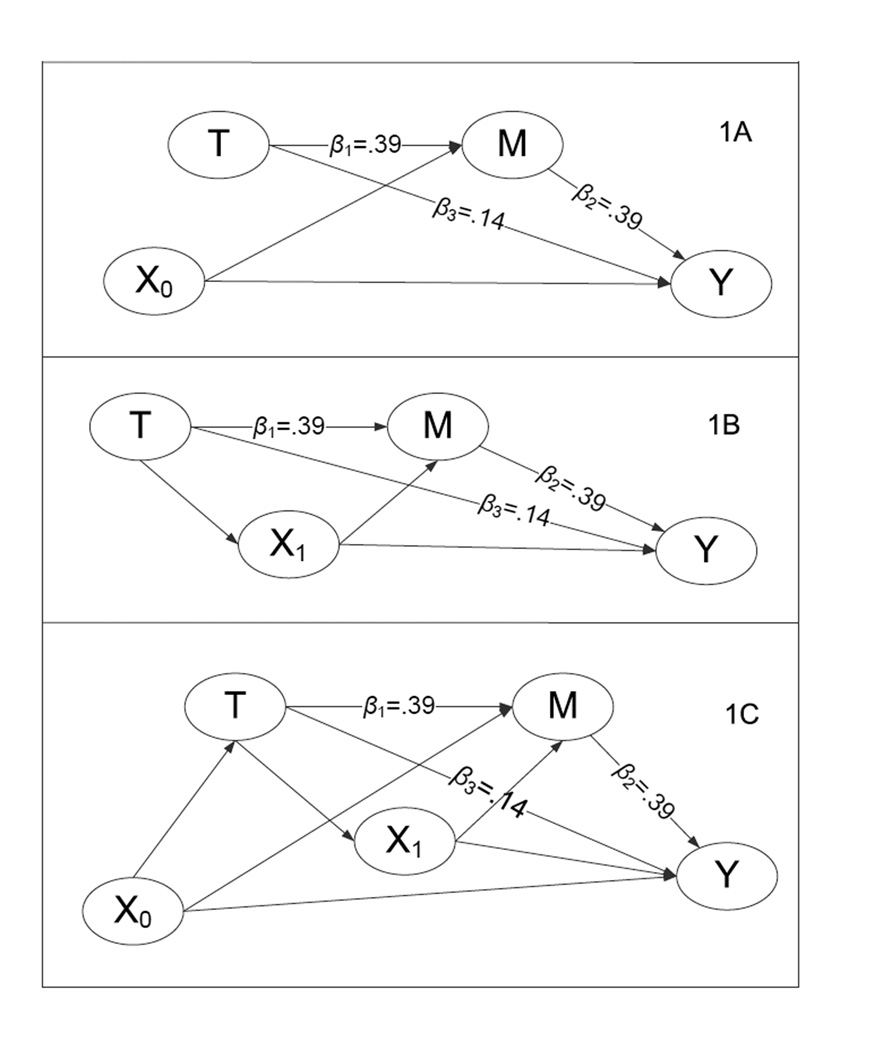
The Monte Carlo simulation study will focus on three different confounding scenarios illustrated in Figure 1: a baseline (i.e., time-invariant) confounder, X0, of M and Y (Panel 1A); a confounder, X1, of M and Y that has been influenced by the treatment (i.e., a post-treatment confounder; Panel 1B); and both a post-treatment confounder, X1, of M and Y and a baseline confounder, X0, of T, M, and Y (i.e., T is not randomized in this condition; Panel 1C). These three confounding scenarios are crossed with four interaction conditions: no interactions (see Figure 1); an interaction between a baseline moderator, Z, and T (see Figure 2); an interaction between Z and M (see Figure 3); and an interaction between T and M (see Figure 4), resulting in 12 conditions. The sample size is 500 in all conditions, and the mediator is a continuous variable. In this section, we will first describe the data generation in detail, then we will define the causal effects of interest for each condition using MSMs. Finally, we will present the models fitted to the data using each estimation method.
Figure 1.
Data-generating confounding structures for simulation study with no moderator. Unless otherwise marked, all paths are .2.
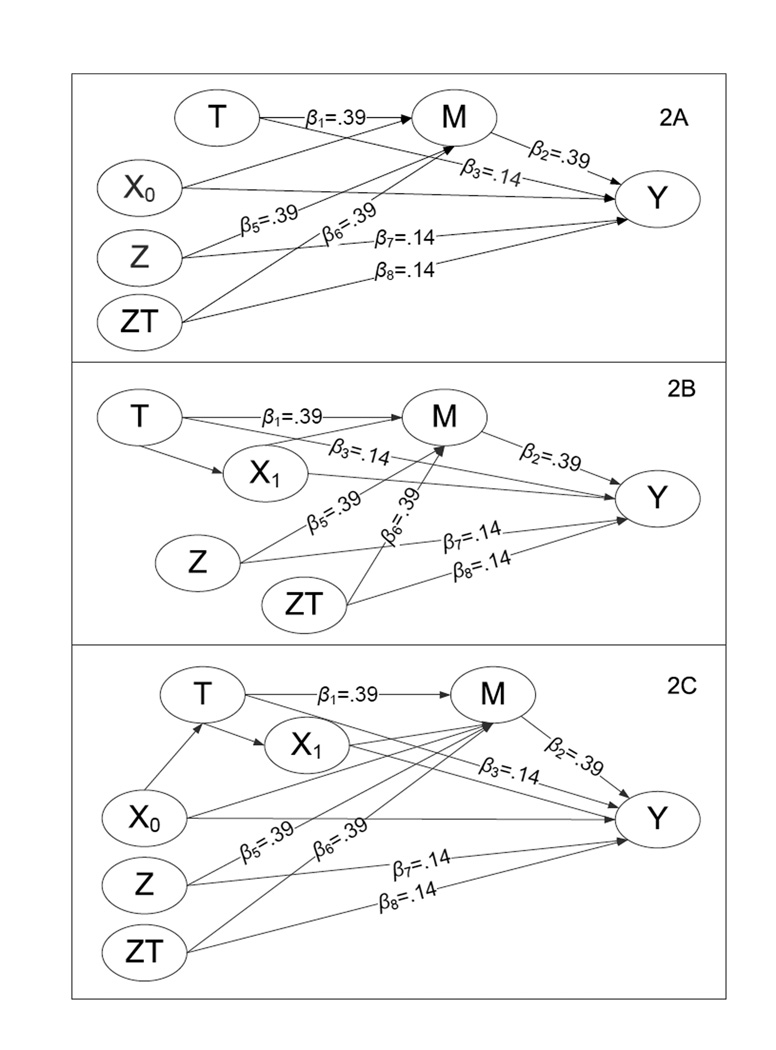
Figure 2.
Data-generating confounding structures for simulation study with an interaction between T and Z. Unless otherwise marked, all paths are .2.
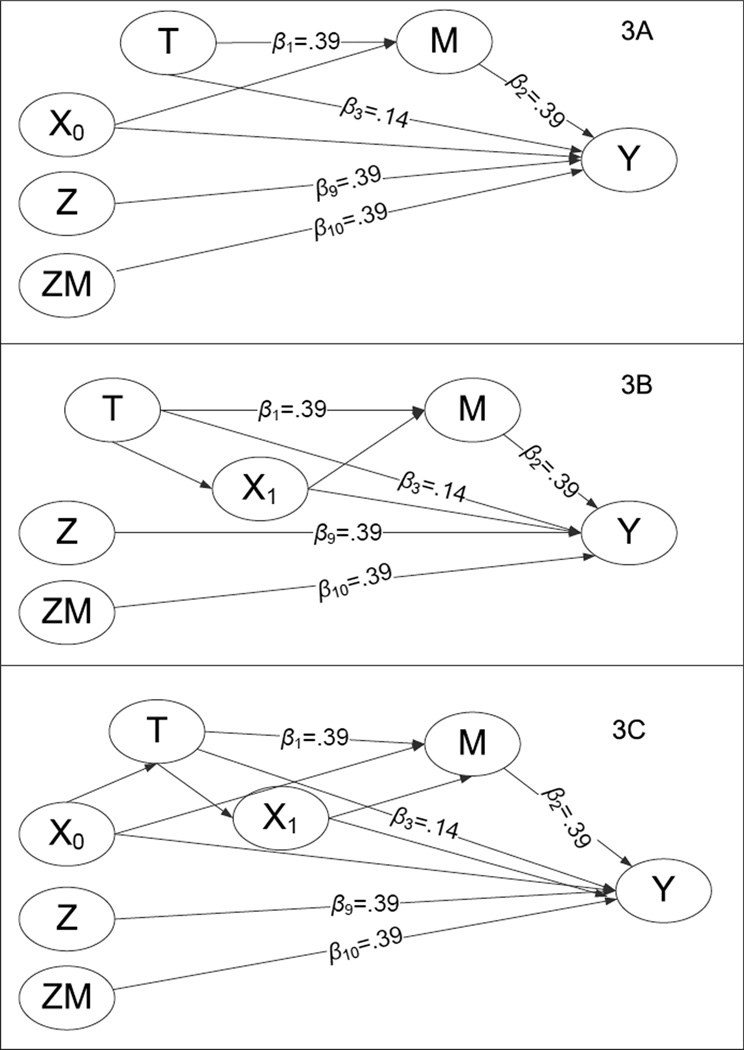
Figure 3.
Data-generating confounding structures for simulation study with an interaction between M and Z. Unless otherwise marked, all paths are .2.
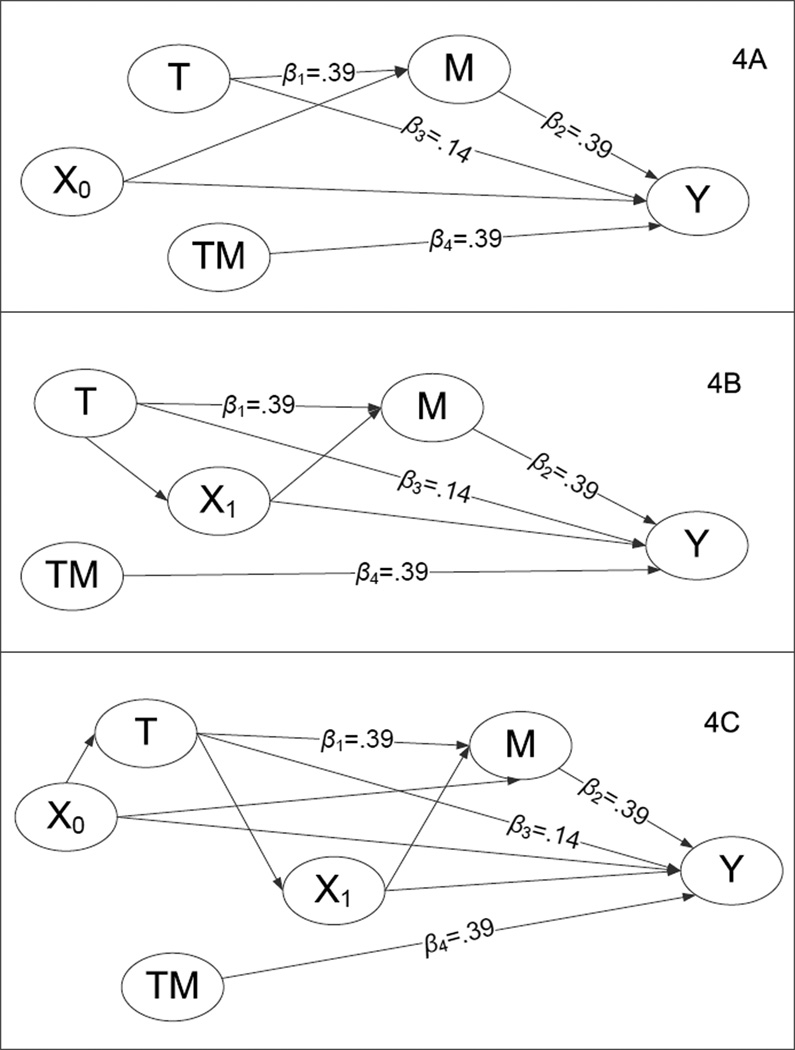
Figure 4.
Data-generating confounding structures for simulation study with an interaction between T and M. Unless otherwise marked, all paths are .2.
Data Generation
In all data generating models, population parameter values for the effect of T on M and for the effect of M on Y conditional on T were chosen to correspond to medium effects (i.e., .39). A small effect (i.e., .14) was chosen for the direct effect for all data-generating models. See Cohen (1988) and MacKinnon, Lockwood, Hoffman, West, and Sheets (2002) for effect size definitions. The moderated effects of an interaction between Z and T (i.e., β6) and between Z and M (i.e., β10) are also .39. All of these effects can be read directly from Figures 1 – 4. Unless otherwise marked, all paths in Figures 1 – 4 are .2. Both confounders, X0 and X1, and M and Y were generated as continuous variables with a standard normal random error. T and Z were generated as binary variables. Note that Figures 1 – 4 are time-ordered from left to right.
For the simulation study, there is only one baseline confounder. However, there could be (and in practice, likely are) many baseline confounders, in which case X0 would represent a vector. Likewise, there is only one post-treatment confounder, although there may be more than one of these, in which case X1 would represent a vector.
Defining the Causal Estimands
In the description of MSMs in the introduction, we defined the causal estimands of interest when there are interactions between T and M and between T and Z. Here, we use MSMs to define the causal estimands of interest when there is an interaction between Z and M. When there is an interaction between Z and M, the MSMs may be given as
| (14) |
and
| (15) |
The causal estimands of interest are
| (16) |
and
| (17) |
for t = 1, and
| (18) |
for t = 0.
Estimation of the Causal Effects
We will use three methods for estimating the causal effects: IPW, an OLS regression adjustment for confounding, and an OLS regression in which there is no adjustment for confounding.
IPW estimator
Given no-interference, treatment-variation irrelevance, consistency, and Assumptions A–C, we can write the MSMs in terms of observed outcomes; these are the models we will fit to the data using IPW estimation. For the conditions with an interaction between T and Z, the models for the observed data are
| (19) |
and
| (20) |
For the conditions with an interaction between Z and M, the models for the observed outcomes are
| (21) |
and
| (22) |
Equations 12 and 13 give the models for the observed outcomes for the conditions with an interaction between T and M.
Unadjusted
Note that these models for the observed data are the same ones that are fit to obtain the unadjusted estimates. However, in this case the estimator is OLS rather than IPW, so there is no adjustment for the confounding.
Regression adjustment
We will adjust for confounding using a regression adjustment. That is, the following models will be fit using OLS:
| (23) |
| (24) |
for Model A in Figure 1,
| (25) |
| (26) |
for Model B in Figure 1, and
| (27) |
| (28) |
for Model C in Figure 1 and likewise for the interaction conditions in Figures 2 – 4.
Assessing Bias and Other Outcome Measures
The population values for the effects can be derived from Figure 1. For Model A, the effect of T on M is .39. Given that X1 is considered a confounder for Models B and C, the total effect of T on M is .43 (i.e., .39+(.2)(.2)=.43), because the data were generated from a linear model. For Models A, B, and C, the effect of M on Y, given T is .39. For Model A, the effect of T on Y, given M is .14. For Models B and C, this effect is .18 (i.e., .14+(.2)(.2)=.18), again considering X1 to be a confounder that is not of substantive interest.
By direct effect of T on Y, we mean all effects that do not go through M (i.e., those that occur through all post-treatment confounders as well as the effect of T on Y). This distinction is important. If the researcher is interested in parsing the direct effect into the effect that goes through X1, then X1 is really another mediator and not a confounder. If the researcher is interested in the question, "What is the effect of T on Y that does not go through M?” then the correct answer is .18. If, on the other hand, the researcher is interested in the question, “What is the effect of T on Y that does not go through M or X1?” then the correct answer is .14. We are presuming that X1 is not of scientific interest, and that the researcher wishes to answer the former question. Thus, it is important to consider the research question, and therefore, the causal effect of interest.
Outcomes of interest from the simulation study are the Monte Carlo (MC) mean and standard deviation (SD), computed as
| (29) |
and
| (30) |
where r is the number of replications (i.e., r = 1000) and θ̂ is a vector containing the estimates. The bias is then given as (θ̅ – θ) where θ contains the true population values.
Testing the Mediated Effect
When there are no interactions (see Figure 1), the test of Effects 1 and 2 is a test of the null hypothesis that β1 = 0 or β2 = 0 (or both are 0). However, when there is an interaction, whether between T and M or involving a baseline confounder, Z, the parameters for the null hypothesis differ. Specifically, if there is an interaction between T and Z (see Figure 2), the null hypothesis is that β1 + β6 = 0 or β2 = 0 (or both are 0). If there is an interaction between M and Z (see Figure 3), the null hypothesis is that β1 = 0 or β2 + β10 = 0 (or both are 0). Finally, when there is an interaction between T and M (see Figure 4), the null hypothesis is that β1 = 0 or β2 + β4 = 0 (or both are 0). To determine the power of this test, we counted the number of times that the test rejected the false null hypothesis, divided by r = 1000.
Simulation Study: Results
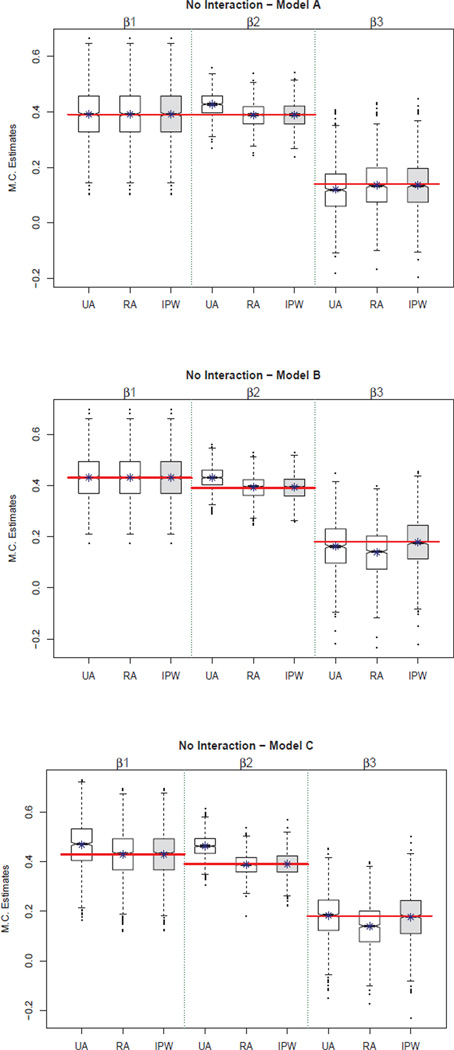
Presence of a Baseline Confounder, X0, of M and Y (Model A)
For Model A in Figure 5, estimates of the effect of T on M are unbiased for all three methods in the presence of a baseline confounder, X0, of M and Y. This result is to be expected because T was randomized. However, for Effect 2 (i.e., β2), and the direct effect (i.e., β3), only regression adjustment and IPW are unbiased. The unadjusted model results in biased estimates as expected. Using path analysis rules, we would expect that the bias in the direct effect, when not adjusting for confounders is .39 * (−.2) * .2 = −.0156. In the no-interaction condition, the bias was −.02 for the unadjusted model. Unbiased estimates can be obtained using either IPW or regression adjustment for this confounding condition regardless of interaction condition (see Figures 6 – 8).
Figure 5.
Boxplots illustrating bias for the unadjusted (UA), regression-adjusted (RA), and inverse propensity weighted (IPW) estimates for the no-interaction models.
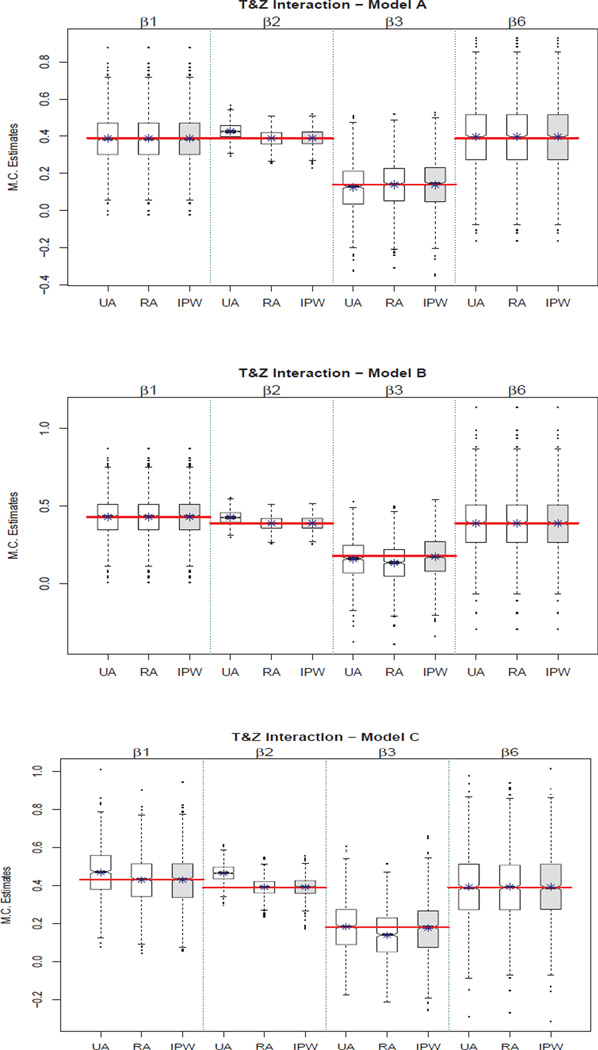
Figure 6.
Boxplots illustrating bias for the unadjusted (UA), regression-adjusted (RA), and inverse propensity weighted (IPW) estimates for the models with an interaction between T and Z.
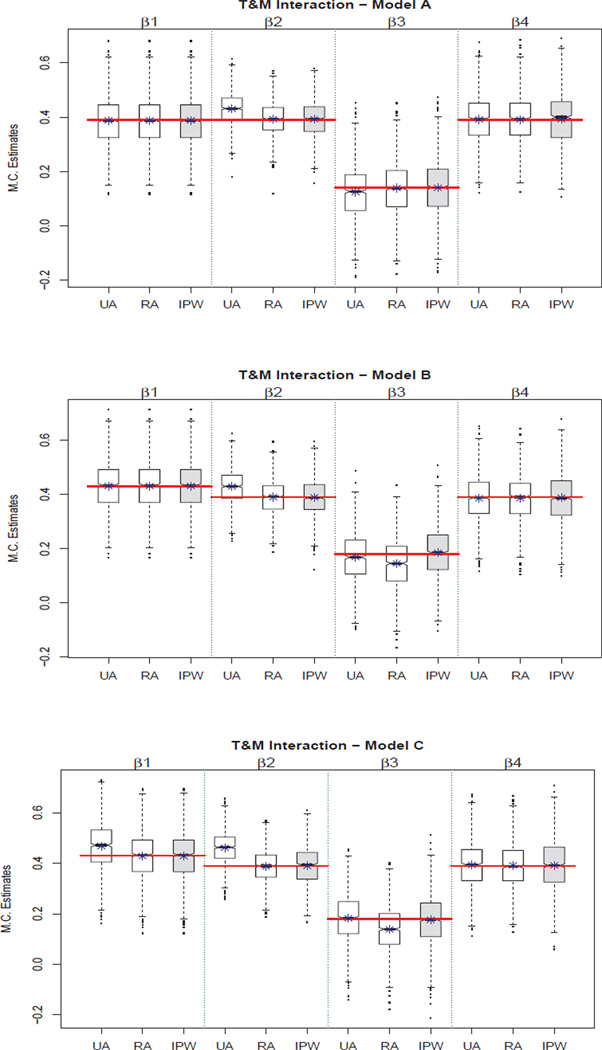
Figure 8.
Boxplots illustrating bias for the unadjusted (UA), regression-adjusted (RA), and inverse propensity weighted (IPW) estimates for the models with an interaction between T and M.
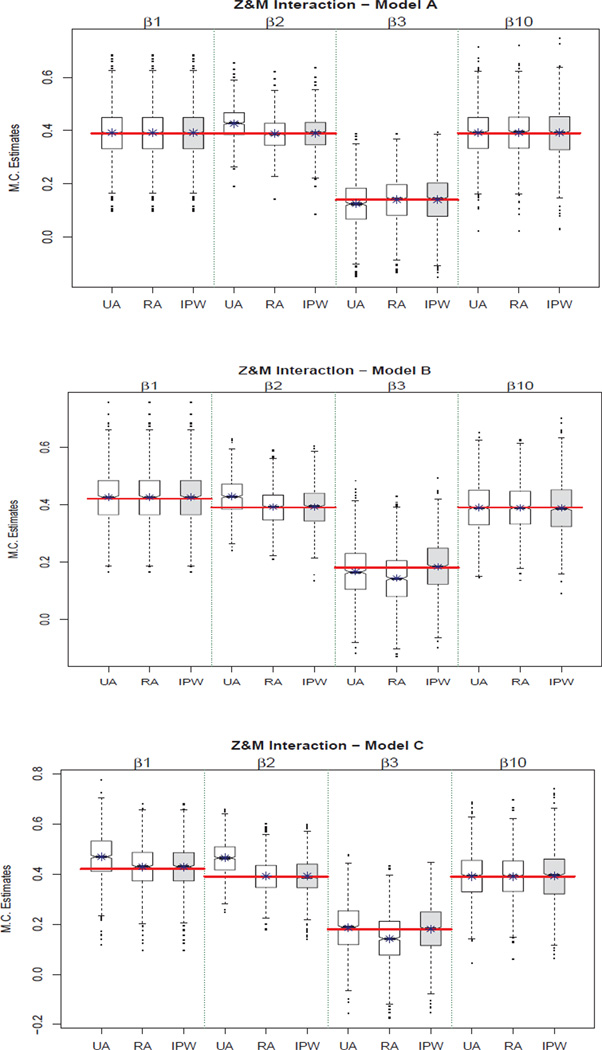
Presence of a Post-Treatment Confounder, X1, of M and Y that has been Influenced by T (Model B)
For Model B in Figure 5, estimates of Effect 1 are unbiased for all three methods, which again is to be expected because T is randomized. However, only IPW provides unbiased estimates of both Effect 2 and the direct effect. The “naive” regression adjustment provides biased estimates of the direct effect, and the unadjusted model provides biased estimates of both the direct effect and Effect 2. Here, we refer to the regression adjustment as “naive” because although it may seem like the natural thing to do, it is incorrect. In this case, the only unbiased option for all effects among those considered is IPW and this result held across all interaction conditions (see Figures 6 – 8). Thus, although there is only one confounder in this case and it may seem troublesome to set up a propensity model for one confounder and create weights, it is nevertheless necessary to properly adjust for confounding.
Presence of Both a Baseline Confounder, X0, of T, M, and Y and a Post-Treatment Confounder, X1, of M and Y (Model C)
For Model C in Figure 5, estimates of Effect 1 are unbiased only for the regression adjustment and IPW methods. This result was expected because in this confounding condition there was no longer randomization to T. Therefore, the unadjusted estimate is biased. As in the previous confounding condition, only IPW provides unbiased estimates of both the direct effect and Effect 2. The “naive” regression adjustment provides biased estimates of the direct effect, and the unadjusted model provides biased estimates of both the direct effect and Effect 2. This result is due to conditioning on a post-treatment confounder that has been influenced by T. Again, IPW is the only unbiased option of those considered for all effects and this result held across interaction conditions (see Figures 6 – 8).
Testing the Mediation Effect
Table 3 presents the empirical power (across the 1000 replications) and confirms that the test has adequate power well above .80 to reject the false null hypothesis that either (or both) of the effects involved in mediation are zero. In addition to confirming adequate power of the mediation test based on IPW estimates, we also tested the accuracy of the IPW estimates by conducting a multivariate Wald test in which the null hypothesis was that the estimates were equal to the true population values. Table 4 presents the Type I error (across the 1000 replications). Failing to reject this null hypothesis indicates that the estimates are not significantly different from the true population estimates (i.e., the estimates are unbiased).
Table 3.
Empirical Power for Testing the Null Hypothesis of No Mediation (1000 replications)
| Test H0 | Model | Power |
|---|---|---|
| No Interaction | Model A | 0.987 |
| H0 : β1 = 0 or β2 = 0 | Model B | 0.999 |
| Model C | 0.993 | |
| T & Z Interaction | Model A | 1.000 |
| H0 : β1 + β6 = 0 or β2 = 0 | Model B | 1.000 |
| Model C | 0.998 | |
| M & Z Interaction | Model A | 0.986 |
| H0 : β1 = 0 or β2 + β10 = 0 | Model B | 0.994 |
| Model C | 0.992 | |
| T & M Interaction | Model A | 0.987 |
| H0 : β1 = 0 or β2 + β4 = 0 | Model B | 0.999 |
| Model C | 0.995 | |
- E[M(t)] = β0M + β1t
- E[Y(t, m)] = β0Y + β2m + β3t
- E[M(t)] = β0M + β1t + β5z + β6zt
- E[Y(t, m)] = β0Y + β2m + β3t + β9z + β10zm
- E[Y(t, m)] = β0Y + β2m + β3t + β4tm
Table 4.
Type I Error for Testing the Accuracy of Estimates Using IPW
| Interaction | Test H0 | Model | Type I Error |
|---|---|---|---|
| None | H0 : β1 = 0.39 & β2 = 0.39 | Model A | 0.057 |
| H0 : β1 = 0.43 & β2 = 0.39 | Model B | 0.043 | |
| H0 : β1 = 0.43 & β2 = 0.39 | Model C | 0.043 | |
| T & Z | H0 : β1 + β6 = 0.78 & β2 = 0.39 | Model A | 0.047 |
| H0 : β1 + β6 = 0.82 & β2 = 0.39 | Model B | 0.064 | |
| H0 : β1 + β6 = 0.82 & β2 = 0.39 | Model C | 0.064 | |
| M & Z | H0 : β1= 0.39 & β2 + β10 = 0.78 | Model A | 0.060 |
| H0 : β1 = 0.43 & β2 + β10 = 0.78 | Model B | 0.081 | |
| H0 : β1 = 0.43 & β2 + β10 = 0.78 | Model C | 0.081 | |
| T & M | H0 : β1 = 0.39 & β2 + β4 = 0.78 | Model A | 0.059 |
| H0 : β1 = 0.43 & β2 + β4 = 0.78 | Model B | 0.046 | |
| H0 : β1 = 0.43 & β2 + β4 = 0.78 | Model C | 0.046 |
Empirical Data Example
Here, we consider a data set that has often been used in methodological articles about causal inference and mediation (e.g., Imai, Keele, & Tingley, 2010; Jo, 2008). In the appendix, we provide the R code for implementing IPW and the test to assess mediation in this example. The data set is from the Job Search Intervention Study (JOBS II; Vinokur & Schul, 1997) and is available as part of the R package mediation (Keele, Tingley, Yamamoto, & Imai, 2009). In this study, 1801 unemployed workers were randomly assigned to treatment or control groups. Those in the treatment group attended job-skills workshops and those in the control group received a booklet of job-search tips. At follow-up interviews the mediator, job-search self-efficacy, was measured along with the outcome, a measure of depressive symptoms based on the Hopkins Symptom Checklist (Derogatis, Lipman, Rickels, Uhlenhuth, & Covi, 1974). Prior to administration of the treatment numerous baseline variables were measured that may potentially be confounders of job-search self-efficacy and depressive symptoms. These included baseline depressive symptoms, education, income, race, marital status, age, gender, previous occupation, and level of economic hardship. We consider a baseline moderator, gender, that may interact with either the intervention or job-search self-efficacy. Finally, we consider the case in which the intervention interacts with job-search self-efficacy.
Define Causal Effects
No interaction between the intervention and job-search self-efficacy
First, we define the causal effects of interest. The causal effect of the intervention on job-search self-efficacy was previously defined as β1 in Equation 3. The causal effect of job-search self-efficacy on depressive symptoms, given intervention status is
| (31) |
for t = 0. Since there is no interaction between intervention status and job-search self-efficacy, the causal effect for t = 1 is the same,
| (32) |
.
Interaction between intervention and gender
The causal effects of interest are given in Equations 8, 9, and 10. Since there is not an interaction between intervention status and job-search self-efficacy, the causal effect defined by Equation 9 is the same as that defined by Equation 10. The causal effect defined by Equation 8 is conditional on gender.
Interaction between job-search self-efficacy and gender
The causal effects of interest are given in Equations 16, 17, and 18. Since there is not an interaction between intervention status and job-search self-efficacy, the causal effect defined by Equation 17 is the same as that defined by Equation 18, although it is conditional on gender.
Interaction between intervention and job-search self-efficacy
The causal effects of interest are given in Equations 3, 4, and 5. Because there is an interaction between intervention status and job-search self-efficacy, the causal effect of job-search self-efficacy on depressive symptoms differs depending on whether the individual received the intervention or not (see Equations 4 and 5).
Estimation
We fit the model using the same three estimation methods as in the simulation study. Since the intervention was randomized, we did not need to adjust for confounding of the effect of the intervention on job-search self-efficacy. As a result, the estimate, .067 (.052), is the same for all three methods (see Table 5) for models with no interaction, an interaction between the intervention and job-search self-efficacy, and an interaction between job-search self-efficacy and gender. This estimate was not statistically significant. For the model with an interaction between the intervention and gender, the estimate was .043 (.078) for all three methods (see Table 5), which was not statistically significant. Also for this model, the estimate for the interaction term (labeled β6 in Table 5) is the same across all three methods because the intervention was randomly assigned.
Table 5.
Results of Empirical Data Analysis.
| Interaction | Parameters | Unadjusted | Reg. Adjust | IPW |
|---|---|---|---|---|
| None | β1(SE) | 0.067 (0.052) | 0.067 (0.052) | 0.067 (0.052) |
| β2(SE) | −0.225 (0.029) | −0.177 (0.028) | −0.194 (0.034) | |
| β3(SE) | −0.048 (0.045) | −0.037 (0.041) | −0.038 (0.049) | |
| T & Z | β1(SE) | 0.043 (0.078) | 0.043 (0.078) | 0.043 (0.078) |
| (Treat & Gender) | β2(SE) | −0.225 (0.029) | −0.177 (0.028) | −0.194 (0.033) |
| β3(SE) | −0.059 (0.067) | −0.046 (0.061) | −0.039 (0.071) | |
| β6(SE) | 0.042 (0.104) | 0.042 (0.104) | 0.042 (0.104) | |
| M & Z | β1(SE) | 0.067 (0.052) | 0.067 (0.052) | 0.067 (0.052) |
| (Job-Seek & Gender) | β2(SE) | −0.211 (0.045) | −0.171 (0.042) | −0.190 (0.046) |
| β3(SE) | −0.043 (0.045) | −0.037 (0.041) | −0.031 (0.049) | |
| β3(SE) | −0.024 (0.058) | −0.010 (0.054) | −0.007 (0.066) | |
| T & M | β1(SE) | 0.067 (0.052) | 0.067 (0.052) | 0.067 (0.052) |
| (Treat & Job_Seek) | β2(SE) | −0.270 (0.053) | −0.240 (0.050) | −0.214 (0.064) |
| β3(SE) | −0.047 (0.045) | −0.035 (0.041) | −0.037 (0.049) | |
| β4(SE) | 0.065 (0.063) | 0.088 (0.058) | 0.029 (0.076) | |
- E[M(t)] = β0M + β1t
- E[Y(t, m)] = β0Y + β2m + β3t
- E[M(t)] = β0M + β1t + β5z + β6zt
- E[Y(t, m)] = β0Y + β2m + β3t + β9z + β10zm
- E[Y(t, m)] = β0Y + β2m + β3t + β4tm
The effect of job-search self-efficacy on depressive symptoms, given intervention status (labeled β2 in Table 5), differed depending on whether and how the confounders were adjusted for. This pattern held across interaction conditions. The general pattern was that the effect of job-search self-efficacy on depressive symptoms was negative. Thus, higher job-search self-efficacy resulted in fewer depressive symptoms. The effect was greatest for the unadjusted model and least for the regression adjusted model. Finally, the effect of the intervention on depressive symptoms, given job-search self-efficacy (labeled β3 in Table 5) differed depending on whether and how the confounders were adjusted for.
Testing the Mediated Effect
We performed the test of the null hypothesis of no mediation only for the IPW estimates. The test indicated that at least one of the estimates was not significantly different from zero (i.e., p = .251 for no-interaction model, p = .267 for the model with an interaction between gender and the intervention, p = .259 for the model with an interaction between gender and job-search self-efficacy, and p = .287 for the model with an interaction between the intervention and job-search self-efficacy). Thus, we fail to reject the null hypothesis of no mediation.
Summary
In comparing these estimates and considering the previous simulation results, we can conclude that an adjustment for confounding is needed in this example. Even though we do not know the true population values, we do know that the unadjusted estimates are different from either the IPW or regression adjustment estimates. The standard errors are slightly larger for IPW because they take into account the uncertainty in estimating the propensity scores.
Discussion
We have illustrated how to define the causal effects of interest in mediation using MSMs, how to estimate these effects using IPW in the presence of both baseline and post-treatment confounders, and how to test the causal effects involved in mediation. The results of the simulation study showed that the test had adequate power to detect mediation. Further, results showed that, in the presence of interactions and non-randomized treatments, the IPW estimator provided unbiased estimates of the causal effects. Finally, we illustrated this approach using an empirical data set.
In general, standard regression methods should not be used to adjust for confounders that have been influenced by T. In the mediation context, IPW can properly control for confounding in which the confounder of the mediator-to-outcome relationship has been influenced by the treatment. When all confounders are pre-treatment, then either the standard regression adjustment or IPW provide unbiased estimates. However, IPW can be advantageous compared to the standard regression adjustment when X0 is a vector that could contain many (e.g., 80) confounders. In this case, adding all the potential confounders as covariates in a regression model would be impractical. IPW also has the advantage that the confounders are not in the regression model for the outcome and, therefore, the causal effects of interest are not conditional on particular values of the confounders.
Previous work (e.g., Coffman, 2011; Y. Li, Bienias, & Bennett, 2007) has stressed the importance of addressing confounding when assessing mediation. In fact, Judd and Kenny (1981), which predates the often-cited Baron and Kenny (1986) paper on mediation, stressed the importance of addressing confounding. However, the importance of addressing confounding has been lost for many years. Because it is generally not possible to randomly assign individuals to M, in most behavioral studies, there are confounders of M and Y. If individuals are not randomly assigned to T, then there are likely to be confounders of T, M, and Y. The simulation study illustrated that it is not only important to address confounding but it is also important to consider how to properly adjust for confounding when assessing mediation. Like failing to adjust for confounders, improper adjustment can result in biased estimates. IPW provided unbiased estimates of all effects even in the presence of post-treatment confounders.
It should be noted that mediation and confounding are statistically equivalent (MacKinnon et al., 2000) and that the difference between a mediator and a confounder is substantive. This is important because a post-treatment confounder is statistically equivalent to a mediator of the effect of T on M. Suppose that a researcher is interested in X1 as a mediator itself and wishes to know the effect of T on Y that occurs through X1 (see Figure 1, Model B). In this case, it would not make sense to treat X1 as a confounder in the denominator model for creating the weights. We have assumed that the researcher is not interested in the effect of T on M that occurs through X1; rather, they are interested in the total effect of T on M.
It should also be noted that regression adjustment of a post-treatment confounder results in bias in only the direct effect. Therefore, it may be tempting to conclude that regression adjustment is fine as long as one is interested primarily in Effect 2. Although the researcher may not be primarily interested in the direct effect, it is nevertheless important to have an unbiased estimate of it, for two reasons. First, if there is no interaction between T and M, then an unbiased estimate of the direct effect can be subtracted from the total effect to obtain an estimate of the indirect effect. Second, it is possible that the direct effect is large and iatrogenic; even if one is primarily interested in the indirect effect, it is important to know that the treatment is not having iatrogenic effects through some other variable(s).
The joint significance test as presented in MacKinnon, Lockwood, et al. (2002) is a possible alternative to the test proposed here, with several key differences. First, the joint significance test does not take into account the covariance between β1 and β2. Second, and more importantly, they test different null hypotheses. The joint significance test tests null hypotheses of the form H0 : β1 = 0 and H0 : β2 = 0 whereas the test proposed here tests null hypotheses of the form H0 : β1 = 0 or β2 = 0. In some situations, the two tests may lead to the same substantive conclusion; nevertheless, they test different null hypotheses and, therefore, may not reach the same substantive conclusion.
Limitations
The assumptions that we made, if they are not plausible in a given empirical example, may be considered limitations. As a reminder, we assumed no-interference, treatment-variation irrelevance, consistency, and that all confounders were measured and included in the propensity model for the denominator of the weights for both the treatment and mediator. A practical limitation is that extremely small propensity scores can result in extremely large weights, which can result in unstable estimates (Kang & Schafer, 2007). Generally, researchers handle this situation by either trimming the weights or removing individuals with extremely large or small weights, thereby limiting causal inference to the sub-sample remaining. For example, to trim the weights, weights less than a particular value such as .05 are set to .05 and weights larger than a particular value such as 15 are set to 15. The choice of a particular value at which to trim the weights or remove individuals from the sample is basically arbitrary and, thus, there is not an optimal strategy for handling extreme weights. The presence of extremely small propensity scores is an indication that the positivity assumption may be violated (Westreich & Cole, 2010). When this assumption is violated, Robins has proposed other methods for causal inference, such as g-computation (Robins, 1986) and g-estimation (Robins, 1989), and a solution may be to pursue one of these other estimators.
Future Directions
Since MSMs and IPW are typically used to assess the effects of time-varying treatments, one obvious future direction is extension of these models to time-varying mediators as well as time-varying treatments in the presence of time-varying confounders. Other possible future directions are to examine different models for estimating the propensity scores, such as generalized boosted modeling (GBM), or other methods of estimation besides IPW.
Conclusions
Much has been written, primarily in the statistics and epidemiology literature, about direct and indirect effects and the potential outcomes framework (Albert, 2007; Emsley et al., 2010; Gallop et al., 2009; Hafeman & VanderWeele, 2010; Jo, 2008; Lynch, Kerry, Gallop, & Ten Have, 2008; Pearl, 2001; Robins & Greenland, 1992; Rubin, 2004; Sobel, 2008; Ten Have et al., 2007; VanderWeele, 2009). Much of this literature (e.g., Emsley et al., 2010; Sobel, 2008; VanderWeele, 2009) has primarily focused on defining direct and indirect effects because there are several subtly different definitions of direct and indirect effects within the potential outcomes framework. We propose an approach in which the causal effects of T on M, M on Y given T = t, and T on Y given M = m are defined in terms of potential outcomes using MSMs and these effects are identified using Assumptions A–C in Table 2. Then, IPW is used to estimate these effects using observed data and finally the null hypothesis that either or both of Effects 1 and 2 are zero serves as a test for mediation.
We have shown that although causal mediation analysis is critically important, it need not be that different from currently implemented methods. Specifically, we clearly defined the causal estimands of interest in terms of potential outcomes using MSMs. Next, we used an IPW estimator to estimate the causal effects and we tested the null hypothesis that either of the effects involved in mediation was zero. We did not identify or estimate the indirect effect itself. However, if Assumption D2 holds, then an estimate of the indirect effect may be obtained by subtracting the direct effect from the total effect.
Figure 7.
Boxplots illustrating bias for the unadjusted (UA), regression-adjusted (RA), and inverse propensity weighted (IPW) estimates for the models with an interaction between M and Z.
Acknowledgments
Preparation of this article was supported by NIDA Center Grant P50 DA100075-15, NIDA R03 DA026543-01, and NIDDK 521 DK082858-2. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute on Drug Abuse (NIDA), the National Institute on Diabetes and Digestive and Kidney Diseases (NIDDK), or the National Institutes of Health (NIH). We would like to thank Daniel Almirall, Amanda Applegate, Bethany Bray, and Kari Kugler for comments on a previous draft of this manuscript.
Appendix
Wald Test with Delta Method for Testing the Hypothesis
The null hypothesis is equivalent to
We denote f(β1, β2) = β1β2, and apply the delta method to it. Asymptotically,
where Σ is the 2 × 2 covariance matrix. By the delta method (or Taylor’s expansion approximation),
Then
where
When the sample size is large enough, we can use the estimates of β1 and β2 and the bootstrapped estimate of Σ to estimate the above τ2, say τ̂2. Now we can construct the Wald test for the null hypothesis H0 : β1 = 0 or β2 = 0.
and the p-value= 2[1 − Φ(|W|)]. If p < 0.05, then we will reject H0.
R code for empirical data analysis
library(mediation)
library(twang)
data("jobs")
# mean center job_seek => job_seek.c
jobs$job_seek.c <- jobs$job_seek - mean(jobs$job_seek)
attach(jobs)
#Analyze jobs data
###########################################################################
# No interactions
# no adjustment
mod.m1 <- lm(job_seek.c ~ treat)
mod.y1 <- lm(depress2 ~ treat + job_seek.c)
# reg. adjustment
mod.y2 <- lm(depress2 ~ treat + job_seek.c + depress1 + econ_hard + sex + age
+ occp + marital + nonwhite + educ + income)
#propensity models for continuous mediator
num.mod <- lm(job_seek.c ~ treat, data=jobs)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=jobs)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
jobs$w.m <- num.p/den.p
# MSM - with robust SE
design.ps <- svydesign(ids= ~1, weights= ~jobs$w.m, data=jobs)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c, design=design.ps)
# Bootstrapping to estimate the covariance matrix
mod1.Boot.ab<-function(dat, n) { # n -- the number of bootstrap replications
a<-c()
b<-c()
ab<-c()
samsize<-dim(dat)[1]
for (i in 1:n) {
resam.num <- sample(samsize,replace=T)
dat.new <- dat[resam.num,]
num.mod <- lm(job_seek.c ~ treat, data=dat.new)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=dat.new)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
jobs$w.m <- num.p/den.p
design.ps <- svydesign(ids= ~1, weights= ~jobs$w.m, data=dat.new)
mod.m3 <- lm(job_seek.c ~ treat, data=dat.new)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c, design=design.ps)
a[i]<-summary(mod.m3)$coef[2,1]
b[i]<-summary(mod.y3)$coef[3,1]
ab[i]<-a[i]*b[i]
}
var.a<-var(a)
var .b<-var(b)
cov.ab<-cov(a,b)
cov.mtx<-matrix(c(var.a,cov.ab,cov.ab,var.b),2,2)
list(a.est=a,b.est=b,ab.est=ab,cov=cov.mtx)
}
boot.mod1=mod1.Boot.ab(jobs,1000)
# Wald Test to test the significance of mediation effects
ahat=summary(mod.m3)$coef[2,1]
bhat=summary(mod.y3)$coef[3,1]
var.new <- c(bhat ,ahat)%*%boot.mod1$cov%*%c(bhat,ahat)
W=bhat*ahat/sqrt(var.new)
pval=2*(1-pnorm(abs(W)))
###########################################################################
# ZT Models
#no adjustment
mod.m1 <- lm(job_seek.c ~ treat + sex + sex*treat)
mod.y1 <- lm(depress2 ~ treat + job_seek.c + sex + sex*treat)
#reg. adjustment
mod.y2 <- lm(depress2 ~ treat + job_seek.c + depress1 + econ_hard + sex + age + occp
+ marital + nonwhite + educ + income + sex*treat)
#propensity models for continuous mediator
num.mod <- lm(job_seek.c ~ sex + treat, data=jobs)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=jobs)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
jobs$w.m <- num.p/den.p
#MSM - with robust SE
design.ps <- svydesign(ids= ~1, weights= ~jobs$w.m, data=jobs)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c + sex + sex*treat, design=design.ps)
# Bootstrapping to estimate the covariance matrix
ztmod1.Boot.ab<-function(dat, n) { # n -- the number of bootstrap replications
a1<-c()
b<-c()
a2<-c()
ab<-c()
samsize<-dim(dat)[1]
for (i in 1:n) {
resam.num <- sample(samsize,replace=T)
dat.new <- dat[resam.num,]
num.mod <- lm(job_seek.c ~ treat + sex, data=dat.new)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=dat.new)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
dat.new$w.m <- num.p/den.p
design.ps <- svydesign(ids= ~1, weights= ~w.m, data=dat.new)
mod.m3 <- lm(job_seek.c ~ treat + sex + sex*treat, data=dat.new)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c + sex + sex*treat, design=design.ps)
a1[i]<-summary(mod.m3)$coef[2,1]
b[i]<-summary(mod.y3)$coef[3,1]
a2[i]<-summary(mod.m3)$coef[4,1] ### for ZT model : beta_6 ###
ab[i] = (a1[i]+a2[i])*b[i]
}
a <- a1+a2
var.a<-var(a)
var .b<-var(b)
cov.ab<-cov(a,b)
cov.mtx<-matrix(c(var.a,cov.ab,cov.ab,var.b),2,2)
list(a1.est=a1,b.est=b,a2.est=a2,ab.est=ab,cov=cov.mtx)
}
boot.ztmod1=ztmod1.Boot.ab(j obs,1000)
# Wald Test to test the significance of mediation effects
ahat=summary(mod.m3)$coef[2,1]+ summary(mod.m3)$coef[4,1]
bhat=summary(mod.y3)$coef[3,1]
var.new <- c(bhat ,ahat)%*%boot .ztmod1$cov%*%c(bhat ,ahat)
W=bhat*ahat/sqrt(var.new)
pval=2*(1-pnorm(abs(W)))
###########################################################################
# ZM Models
#no adjustment
mod.m1 <- lm(job_seek.c ~ treat)
mod.y1 <- lm(depress2 ~ treat + job_seek.c + sex + sex*job_seek.c)
#reg. adjustment
mod.y2 <- lm(depress2 ~ treat + job_seek.c + depress1 + econ_hard + sex + age + occp
+ marital + nonwhite + educ + income + sex*job_seek.c)
#propensity models for continuous mediator
num.mod <- lm(job_seek.c ~ treat + sex, data=jobs)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=jobs)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
jobs$w.m <- num.p/den.p
#MSM - with robust SE
design.ps <- svydesign(ids= ~1, weights= ~jobs$w.m, data=jobs)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c + sex + sex*job_seek.c, design=design.ps)
# Bootstrapping to estimate the covariance matrix
zmmod1.Boot.ab<-function(dat, n) { # n -- the number of bootstrap replications
a<-c()
b1<-c()
b2<-c()
ab<-c()
samsize<-dim(dat)[1]
for (i in 1:n) {
resam.num <- sample(samsize,replace=T)
dat.new <- dat[resam.num,]
num.mod <- lm(job_seek.c ~ treat + sex, data=dat.new)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital
+ nonwhite + educ + income, data=dat.new)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
dat.new$w.m <- num.p/den.p
design.ps <- svydesign(ids= ~1, weights= ~w.m, data=dat.new)
mod.m3 <- lm(job_seek.c ~ treat, data=dat.new)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c + sex + sex*job_seek.c, design=design.ps)
a[i]<-summary(mod.m3)$coef[2,1]
b1[i]<-summary(mod.y3)$coef[3,1]
b2[i]<-summary(mod.y3)$coef[5,1]
ab[i]<-a[i]*(b1[i]+b2[i])
}
b <- b1+b2
var.a<-var(a)
var.b<-var(b)
cov.ab<-cov(a,b)
cov.mtx<-matrix(c(var.a,cov.ab,cov.ab,var.b),2,2)
list(a.est=a,b1.est=b1,b2.est=b2,ab.est=ab,cov=cov.mtx)
}
boot.zmmod1=zmmod1.Boot.ab(jobs,1000)
# Wald Test to test the significance of mediation effects
ahat=summary(mod.m3)$coef[2,1]
bhat=summary(mod.y3)$coef[3,1]+summary(mod.y3)$coef[5,1]
var.new <- c(bhat ,ahat)%*%boot .zmmod1$cov%*%c(bhat ,ahat)
W=bhat*ahat/sqrt(var.new)
pval=2*(1-pnorm(abs(W)))
###########################################################################
# TM Models
#no adjustment
mod.m1 <- lm(job_seek.c ~ treat)
mod.y1 <- lm(depress2 ~ treat + job_seek.c + treat*job_seek.c)
#reg. adjustment
mod.y2 <- lm(depress2 ~ treat + job_seek.c + depress1 + treat*job_seek.c + econ_hard + sex + age
+ occp + marital + nonwhite + educ + income )
#propensity models for continuous mediator
num.mod <- lm(job_seek.c ~ treat, data=jobs)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital + nonwhite
+ educ + income, data=jobs)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
jobs$w.m <- num.p/den.p
#MSM - with robust SE
design.ps <- svydesign(ids= ~1, weights= ~jobs$w.m, data=jobs)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c+ treat*job_seek.c, design=design.ps)
# Bootstrapping to estimate the covariance matrix
tmmod1.Boot.ab<-function(dat, n) { # n -- the number of bootstrap replications
a<-c()
b1<-c()
b2<-c()
ab<-c()
samsize<-dim(dat)[1]
for (i in 1:n) {
resam.num <- sample(samsize,replace=T)
dat.new <- dat[resam.num,]
num.mod <- lm(job_seek.c ~ treat, data=dat.new)
den.mod <- lm(job_seek.c ~ treat + depress1 + econ_hard + sex + age + occp + marital + nonwhite
+ educ + income, data=dat.new)
sigma.n <- summary(num.mod)$sigma
sigma.d <- summary(den.mod)$sigma
num.p <- dnorm(job_seek.c, mean=num.mod$fitted, sd=sigma.n)
den.p <- dnorm(job_seek.c, mean=den.mod$fitted, sd=sigma.d)
dat$w.m <- num.p/den.p
design.ps <- svydesign(ids= ~1, weights= ~w.m, data=dat.new)
mod.m3 <- lm(job_seek.c ~ treat, dat=dat.new)
mod.y3 <- svyglm(depress2 ~ treat + job_seek.c+ treat*job_seek.c, design=design.ps)
a[i]<-summary(mod.m3)$coef[2,1]
b1[i]<-summary(mod.y3)$coef[3,1]
b2[i]<-summary(mod.y3)$coef[4,1]
ab[i]<-a[i]*(b1[i]+b2[i])
}
b <- b1+b2
var.a<-var(a)
var.b<-var(b)
cov.ab<-cov(a,b)
cov.mtx<-matrix(c(var.a,cov.ab,cov.ab,var.b),2,2)
list(a.est=a,b1.est=b1,b2.est=b2,ab.est=ab,cov=cov.mtx)
}
boot.tmmod1=tmmod1.Boot.ab(jobs,1000)
# Wald Test to test the significance of mediation effects
ahat=summary(mod.m3)$coef[2,1]
bhat=summary(mod.y3)$coef[3,1]+summary(mod.y3)$coef[4,1]
var.new <- c(bhat ,ahat)%*%boot .tmmod1$cov%*%c(bhat ,ahat)
W=bhat*ahat/sqrt(var.new)
pval=2*(1-pnorm(abs(W)))
Contributor Information
Donna L. Coffman, Pennsylvania State University
Wei Zhong, Xiamen University.
References
- Albert JM. Mediation analysis via potential outcomes. Statistics in Medicine. 2007;27:1282–1304. doi: 10.1002/sim.3016. [DOI] [PubMed] [Google Scholar]
- Angrist J, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables (with discussion) Journal of the American Statistical Association. 1996;91:444–472. [Google Scholar]
- Avin C, Shipster I, Pearl J. Identifiability of path-specific effects. Proceedings of the international joint conferences on artificial intelligence. 2005:357–363. [Google Scholar]
- Barber JS, Murphy SA, Verbitsky N. Adjusting for time-varying confounding in survival analysis. Sociological Methodology. 2004;34:163–192. [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bodnar LM, Davidian M, Siega-Riz AM, Tsiatis AA. Marginal structural models for analyzing causal effects of time-dependent treatments: An application in perinatal epidemiology. American Journal of Epidemiology. 2004;159:926–934. doi: 10.1093/aje/kwh131. [DOI] [PubMed] [Google Scholar]
- Bray BC, Almirall D, Zimmerman RS, Lynam D, Murphy SA. Assessing the total effect of time-varying predictors in prevention research. Prevention Science. 2006;7:1–17. doi: 10.1007/s11121-005-0023-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman DL. Causal inference for mediation analysis with propensity scores. Structural Equation Modeling. 2011;18:357–369. doi: 10.1080/10705511.2011.582001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale, NJ: LEA; 1988. [Google Scholar]
- Cole SR, Hernan MA. Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology. 2008;168:656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole SR, Hernan MA, Anastos K, Jamieson BD, Robins JM. Determining the effect of highly active antiretroviral therapy on changes in human immunodeficiency virus type 1 RNA viral load using a marginal structural left-censored mean model. American Journal of Epidemiology. 2007;166:219–227. doi: 10.1093/aje/kwm047. [DOI] [PubMed] [Google Scholar]
- Derogatis LR, Lipman RS, Rickels K, Uhlenhuth EH, Covi L. The Hopkins Symptom Checklist (HSCL): A self-report symptom inventory. Behavioral Science. 1974;19:1–15. doi: 10.1002/bs.3830190102. [DOI] [PubMed] [Google Scholar]
- Edwards JR, Lambert LS. Methods for integrating moderation and mediation: A general analytical framework using moderated path analysis. Psychological Methods. 2007;12:1–22. doi: 10.1037/1082-989X.12.1.1. [DOI] [PubMed] [Google Scholar]
- Elliott MR, Raghunathan TE, Li Y. Bayesian inference for causal mediation effects using principal stratification with dichotomous mediators and outcomes. Bio statistics. 2010;11:353–372. doi: 10.1093/biostatistics/kxp060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emsley R, Dunn G, White IR. Mediation and moderation of treatment effects in randomised controlled trials of complex interventions. Statistical Methods in Medical Research. 2010;19:237–270. doi: 10.1177/0962280209105014. [DOI] [PubMed] [Google Scholar]
- Frangakis CE. Principal stratification. In: Gelman A, Meng X-L, editors. Applied bayesian modeling and causal inference from incomplete-data perspectives. Hoboken, NJ: John Wiley & Sons; 2004. [Google Scholar]
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:20–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallop R, Small DS, Lin JY, Elliot MR, Joffe M, Ten Have TR. Mediation analysis with principal stratification. Statistics in Medicine. 2009;28:1108–1130. doi: 10.1002/sim.3533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh D, Elliott MR, Taylor JMG. Links between analysis of surrogate endpoints and endogeneity. Statistics in Medicine. 2010;29:2869–2879. doi: 10.1002/sim.4027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenland S, Morgenstern H. Confounding in health research. Annual Review of Public Health. 2001;22:189–212. doi: 10.1146/annurev.publhealth.22.1.189. [DOI] [PubMed] [Google Scholar]
- Hafeman DM, VanderWeele TJ. Alternative assumptions for the identification of direct and indirect effects. Epidemiology. 2010 doi: 10.1097/EDE.0b013e3181c311b2. [DOI] [PubMed] [Google Scholar]
- Holland PW. Statistics and causal inference. Journal of the American Statistical Association. 1986;81:945–970. [Google Scholar]
- Holland PW. Causal inference, path analysis, and recursive structural equations models. Sociological Methodology. 1988;18:449–484. [Google Scholar]
- Hong G, Raudenbush SW. Effects of kindergarten retention policy on children’s cognitive growth in reading and mathematics. Educational Evaluation and Policy Analysis. 2005;27:205–224. [Google Scholar]
- Hong G, Raudenbush SW. Evaluating kindergarten retention policy: A case study of causal inference for multi-level observational data. Journal of the American Statistical Association. 2006;101:901–910. [Google Scholar]
- Horvitz DG, Thompson DJ. A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association. 1952;47:663–685. [Google Scholar]
- Hudgens MG, Halloran ME. Toward causal inference with interference. Journal of the American Statistical Association. 2008;103:832–842. doi: 10.1198/016214508000000292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15:309–334. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, Yamamoto T. Identification, inference, and sensitivity analysis for causal mediation effects. Statistics in Medicine. 2010;25:51–71. [Google Scholar]
- Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13:314–336. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. [Google Scholar]
- Kang J, Schafer JL. Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science. 2007;22(4):523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keele L, Tingley D, Yamamoto T, Imai K. mediation: R package for causal mediation analysis [Computer software manual] 2009 Available from http://CRAN.R-project.org/package=mediation (R package version 2.1)
- Ko H, Hogan JW, Mayer KH. Estimating causal treatment effects from longitudinal HIV natural history studies using marginal structural models. Biometrics. 2003;59:152–162. doi: 10.1111/1541-0420.00018. [DOI] [PubMed] [Google Scholar]
- Li L, Evans E, Hser Y. A marginal structural modeling approach to assess the cumulative effect of treatment on later drug use abstinence. Journal of Drug Issues. 2010;40:221–240. doi: 10.1177/002204261004000112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Bienias JL, Bennett DA. Confounding in the estimation of mediation effects. Computational Statistics and Data Analysis. 2007;51:3173–3186. doi: 10.1016/j.csda.2006.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA, Rubin DB. Causal effects in clinical and epidemiological studies via potential outcomes: Concepts and analytical approaches. Annual Review of Public Health. 2000;21:121–145. doi: 10.1146/annurev.publhealth.21.1.121. [DOI] [PubMed] [Google Scholar]
- Luellen JK, Shadish WR, Clark MH. Propensity scores: An introduction and experimental test. Evaluation Review. 2005;29:530–558. doi: 10.1177/0193841X05275596. [DOI] [PubMed] [Google Scholar]
- Lumley T. survey: analysis of complex survey samples [Computer software manual] 2010 Available from http://CRAN.R-project.org/package=survey (R package version 3.22-1) [Google Scholar]
- Lynch KG, Kerry M, Gallop R, Ten Have TR. Causal mediation analyses for randomized trials. Health Services Outcomes Research Methodology. 2008;8:57–76. doi: 10.1007/s10742-008-0028-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. New York: LEA; 2008. [Google Scholar]
- MacKinnon DP, Krull JL, Lockwood CM. Equivalence of the mediation, confounding, and suppression effect. Prevention Science. 2000;1:173–181. doi: 10.1023/a:1026595011371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test the significance of the intervening variable effect. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Taborga MP, Morgan-Lopez AA. Mediation designs for tobacco prevention research. Drug and Alcohol Dependence. 2002;68:S69–S83. doi: 10.1016/s0376-8716(02)00216-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- Morgan SL, Winship C. Counterf actuals and causal inference: Methods and principals for social research. New York: Cambridge; 2007. [Google Scholar]
- Mortimer KM, Heugebauer R, van der Laan M, Tager IB. An application of model-fitting procedures for marginal structural models. American Journal of Epidemiology. 2005;162:382–388. doi: 10.1093/aje/kwi208. [DOI] [PubMed] [Google Scholar]
- Muller D, Judd CM, Yzerbyt VY. When moderation is mediated and mediation is moderated. Journal of Personality and Social Psychology. 2005;89:852–863. doi: 10.1037/0022-3514.89.6.852. [DOI] [PubMed] [Google Scholar]
- Pearl J. Direct and indirect effects. In: Besnard P, Hanks S, editors. Proceedings of the seventeenth conference on uncertainty in artificial intelligence. San Francisco: Morgan Kaufman; 2001. [Google Scholar]
- Pearl J. The causal foundations of structural equation modeling (Tech Report No. R-370) UCLA; 2010a. Aug. [Google Scholar]
- Pearl J. The mediation formula: A guide to the assessment of causal pathways in non-linear models (Tech Report No. R-363) UCLA; 2010b. May, [Google Scholar]
- Pearl J. Invited commentary: Understanding bias amplification. American Journal of Epidemiology. 2011;174:1223–1227. doi: 10.1093/aje/kwr352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preacher KJ, Rucker DD, Hayes AF. Assessing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate Behavioral Research. 2007;42:185–227. doi: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- Robins JM. A new approach to causal inference in mortality studies with sustained exposure periods - application to control of the healthy worker survival effect. Mathematical Modelling. 1986;7:1393–1512. [Google Scholar]
- Robins JM. The analysis of randomized and non-randomized AIDS treatment trials using a new approach to causal inference in longitudinal studies. In: Secrest L, Freeman H, Mulley A, editors. Health service research methodology: A focus on AIDS. Washington, DC: US Public Health Service, National Center for Health Services Research; 1989. pp. 113–159. [Google Scholar]
- Robins JM, Greenland S. Identifiability and exchangeability of direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Robins JM, Hernan M, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984;79:516–524. [Google Scholar]
- Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. American Statistician. 1985;39:33–38. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin DB. Direct and indirect causal effects via potential outcomes. Scandinavian Journal of Statistics. 2004;31:161–170. [Google Scholar]
- Rubin DB. Causal inference using potential outcomes: Design, modeling, decisions. Journal of the American Statistical Association. 2005;100:322–331. [Google Scholar]
- Schafer JL, Kang J. Average causal effects from non-randomized studies: A practical guide and simulated example. Psychological Methods. 2008;13(4):279–313. doi: 10.1037/a0014268. [DOI] [PubMed] [Google Scholar]
- Sobel ME. What do randomized studies of housing mobility demonstrate?: Causal inference in the face of interference. Journal of the Statistical Association. 2006;101:1398–1407. [Google Scholar]
- Sobel ME. Identification of causal parameters in randomized studies with mediating variables. Journal of Educational and Behavioral Statistics. 2008;33:230–251. [Google Scholar]
- Steiner PM, Cook TD, Shadish WR, Clark MH. The importance of covariate selection in controlling for selection bias in observational studies. Psychological Methods. 2010;15:250–267. doi: 10.1037/a0018719. [DOI] [PubMed] [Google Scholar]
- Ten Have TR, Joffe M, Lynch K, Maisto S, Brown G, Beck A. Causal mediation analysis with rank-preserving models. Biometrics. 2007;63:926–934. doi: 10.1111/j.1541-0420.2007.00766.x. [DOI] [PubMed] [Google Scholar]
- van der Wal WM, Prins M, Lumbreras B, Geskus RB. A simple G-computation algorithm to quantify the causal effect of a secondary illness on the progression of a chronic disease. Statistics in Medicine. 2009;28:2325–2337. doi: 10.1002/sim.3629. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Ignorability and stability assumptions in neighborhood effects research. Statistics in Medicine. 2008;27:1934–1943. doi: 10.1002/sim.3139. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Simple relations between principal stratification and direct and indirect effects. Statistics and Probability Letters. 2008;78:2957–2962. [Google Scholar]
- VanderWeele TJ. Marginal structural models for the estimation of direct and indirect effects. Epidemiology. 2009;20:18–26. doi: 10.1097/EDE.0b013e31818f69ce. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Direct and indirect effects for neighborhood-based clustered and longitudinal data. Sociological Methods and Research. 2010;38:515–544. doi: 10.1177/0049124110366236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Hawkley LC, Thisted RA, Cacioppo JT. A marginal structural model analysis for loneliness: Implications for intervnetion trials and clinical practice. Journal of Consulting and Clinical Psychology. 2011;79:225–235. doi: 10.1037/a0022610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, interventions, and composition. Statistics and Its Interface. 2009;2:457–468. [Google Scholar]
- Vinokur AD, Schul Y. Mastery and inoculation against setbacks as active ingredients in the JOBS intervention for the unemployed. Journal of Consulting and Clinical Psychology. 1997;65:867–877. doi: 10.1037//0022-006x.65.5.867. [DOI] [PubMed] [Google Scholar]
- West SG, Biesanz JC, Pitts SC. Causal inference and generalization in field settings: Experimental and quasi-experimental designs. In: Reis HTJ, Judd C, editors. Handbook of research methods in social and personality psychology. New York: Cambridge University Press; 2000. pp. 40–84. [Google Scholar]
- Westreich D, Cole S. Invited commentary: Positivity in practice. American Journal of Epidemiology. 2010;171:674–677. doi: 10.1093/aje/kwp436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wimer C, Sampson RJ, Laub JH. Estimating time-varying causes and outcomes with application to incarceration and crime. In: Cohen P, editor. Applied data analytic techniques for turning points research. New York: Routledge; 2008. pp. 37–59. [Google Scholar]
- Winship C, Morgan SL. The estimation of causal effects from observational data. Annual Review of Sociology. 1999;25:659–706. [Google Scholar]