Correlation Analysis of Enzymatic Reaction of a Single Protein Molecule

Abstract

New advances in nano sciences open the door for scientists to study biological processes on a microscopic molecule-by-molecule basis. Recent single-molecule biophysical experiments on enzyme systems, in particular, reveal that enzyme molecules behave fundamentally differently from what classical model predicts. A stochastic network model was previously proposed to explain the experimental discovery. This paper conducts detailed theoretical and data analyses of the stochastic network model, focusing on the correlation structure of the successive reaction times of a single enzyme molecule. We investigate the correlation of experimental fluorescence intensity and the correlation of enzymatic reaction times, and examine the role of substrate concentration in enzymatic reactions. Our study shows that the stochastic network model is capable of explaining the experimental data in depth.

1 Introduction

In a chemical reaction, the number of molecules involved can drastically vary from millions of moles — a forest devastated by a fire — to only a few — reactions in a living cell. While most conventional chemical experiments were designed for a large ensemble in which only average could be observed, chemistry textbooks tend to explain what really happens in a reaction on a molecule-by-molecule basis. This extrapolation certainly requires the homogeneity assumption: each molecule behaves in the same way, so average also represents individual behavior. To verify this assumption, the kinetic of a single molecule must be directly observed, which requires rather sophisticated technology not available until the 1990s. Since then, the development of nanotechnology has enabled scientists to track and manipulate molecules one by one. A new age of single-molecule experiments began (Nie and Zare 1997; Xie and Trautman 1998; Xie and Lu 1999; Tamarat et al. 2000; Weiss 2000; Moerner 2002; Flomenbom et al. 2005; Kou, Xie and Liu 2005b; Kou 2009).

Such experiments offer greatly amplified view of single-molecular dynamics over considerably long time periods from seconds to hours, a time scale that far exceeds what can be achieved by computer based molecular dynamic simulation (even with a super computer, molecular dynamic simulation cannot reach beyond milliseconds). The single-molecule experiments also provide detailed information on the intermediate transition steps of a biological process not available in traditional experiments. Not surprisingly, these experiments reveal the stochastic nature of nanoscale particles long masked by ensemble averages: rather than remain rigid, those particles undergo dramatic conformation change driven by external thermal motion. Future development in this area will provide us a deeper understanding of biological processes (such as molecular motors, Asbury, Fehr and Block, 2003) and accelerate new technology development (such as single-molecule gene sequencing, Pushkarev, Neff, and Quake, 2009).

Among bio-molecules, enzymes play an important role: by lowering the energy barrier between the reactant and product, they ensure that many life essential processes can be effectively carried out in a living cell. An aspiration of bioengineers is to artificially design and produce new and efficient enzymes for specific use. Studying and understanding the mechanism of existing enzymes, therefore, remains one of the central topics in life science. According to the classical literature, the kinetic of an enzyme is described by the Michaelis-Menten mechanism (Atkins and de Paula, 2002): an enzyme molecule E could bind with a reactant molecule S, which is referred to as a substrate in the chemistry literature (hence the symbol S), to form a complex ES. The complex can either dissociate to enzyme and substrate molecules or undergo a catalytic process to release the product P. The enzyme then returns to the original state E to start another catalytic circle. This process is typically diagrammed as

$$E+S\underset{k_{-1}}{\overset{k_1[S]}{\rightleftarrows }}ES\stackrel{k_2}{\to }{E}^0+P,E^0\stackrel{\delta }{\to }E,$$ (1.1)

where [S] is the substrate concentration (E⁰ is the release state of the enzyme), k₁ is the association rate per unit substrate concentration, k₋₁ and k₂ are, respectively, the dissociation and catalytic rate, and δ is the returning rate. All the transitions are memoryless in the Michaelis-Menten scheme, so the whole process can be modeled as a continuous-time Markov chain consisting of three states E, ES and E⁰ for an enzyme molecule.

A recent single-molecule experiment (English et al. 2006) conducted by the Xie group at Harvard University (Department of Chemistry and Chemical Biology) studied the enzyme β-galactosidase (β-gal), which catalyzes the breakdown of the sugar lactose and is essential in the human body (Jacobson et al. 1994, Dorland 2003). In the experiment a single β-gal molecule is immobilized (by linking to a bead bound on a glass coverslip) and immersed in buffer solution of the substrate molecules. This setup allows β-gal’s enzymatic action to be continuously monitored under a fluorescence microscope. To detect the individual turnovers, i.e., the enzyme’s switching from the E state to the E⁰ state, careful design and special treatment were carried out (such as the use of photogenic substrate resorun-β-D-galactopyranoside) so that once the experimental system was placed under a laser beam the reaction product and only the reaction product was fluorescent. This setting ensures that as the β-gal enzyme catalyzes substrate molecules one after another, strong fluorescence signal is emitted and detected only when a product is released, i.e., only when the reaction reaches the E⁰ + P stage in (1.1). Recording the fluorescence intensity over time thus enables the experimental determination of individual turnovers. A sample fluorescence intensity trajectory from this experiment is shown in Figure 1. High spikes in the trajectory are the results of intense photon burst at the E⁰ + P state, while low readings correspond to the E or ES state. The time lag between two adjacent high fluorescence spikes is the enzymatic turnover time, i.e., the time to complete a catalytic circle.

Figure 1.

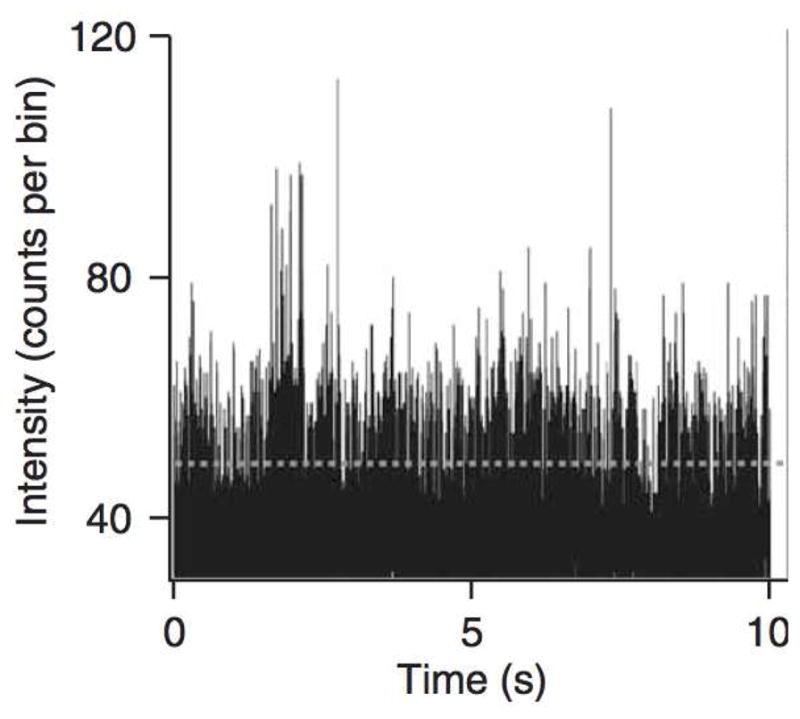
Fluorescence intensity reading from one experiment (the substrate concentration is 100 micro-molar). Each fluorescence intensity spike is caused by the release of a reaction product.

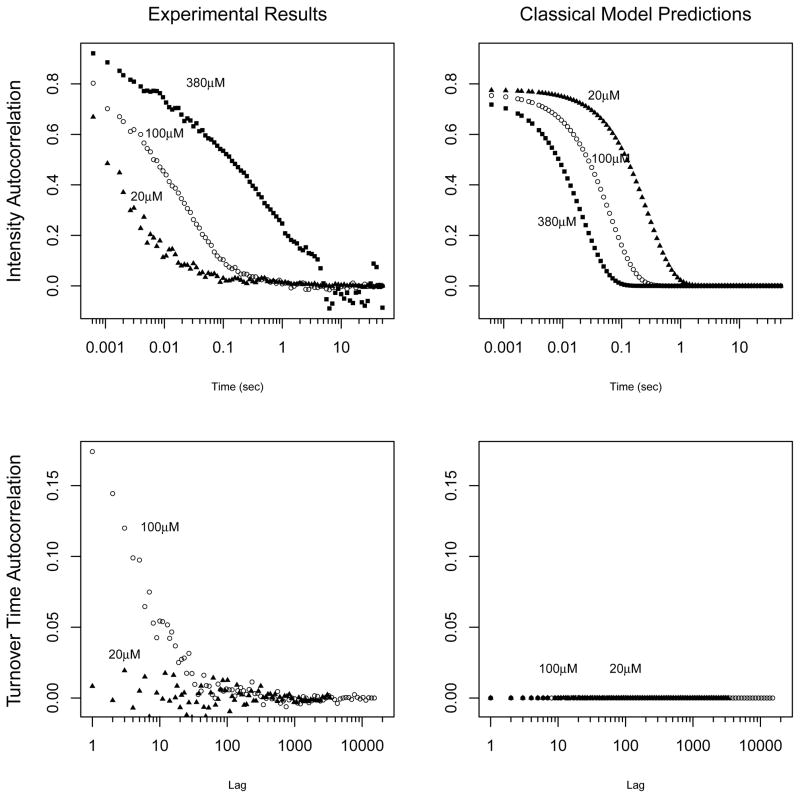
Examining the experimental data, including the distribution and autocorrelation of the turnover times as well as the fluorescence intensity autocorrelation, researchers were surprised that the experimental data showed a considerable departure from the Michaelis-Menten mechanism. Section 2 describes the experimental findings in detail. Figure 2 illustrates the discrepancy between the experimental data and the Michaelis-Menten model in terms of the autocorrelations. The left two panels show the experimentally observed fluorescence intensity autocorrelation and turnover time autocorrelation under different substrate concentrations [S]. The right two panels show the corresponding autocorrelation patterns predicted by the Michaelis-Menten model. Comparing the bottom two panels, we note that under the classical Michaelis-Menten model the turnover time autocorrelation should be zero (hence the horizontal line at the bottom-right panel), which clearly contradicts the experimental result on the left. From the top two panels we note that under the Michaelis-Menten model the fluorescence intensity autocorrelation should decay exponentially and should decay faster with larger substrate concentration, but the experiemental result shows the opposite: the intensity autocorrelations decay slower with larger substrate concentration, and they do not decay exponentially.

Figure 2.

Left column: Experimentally observed fluorescence intensity and turnover time autocorrelations under different substrate concentrations [S] (20, 100 and 380 micromolar). Right column: The autocorrelations predicted by the classical Michaelis-Menten model. Under the Michaelis-Menten model, the turnover time autocorrelation should be zero and the intensity autocorrelations should decay exponentially and decay faster under larger concentration. All contradict the experimental findings.

To explain the experimental puzzle, a new stochastic network model was introduced (Kou et al. 2005a, Kou 2008b), and it was shown that the stochastic network model well explained the experimental distribution of the turnover times. The autocorrelation of successive turnover times and the correlation of experimental fluorescence intensity, however, were not investigated in the previous articles.

This paper further explores the stochastic network model, concentrating on the correlation structure of the turnover times and that of the fluorescence intensity. The rest of the paper is organized as follows. Section 2 reviews the preceding work, including the experiment observation and the new stochastic network model. Section 3 analytically calculates the turnover time autocorrelation and the fluorescence intensity autocorrelation based on the stochastic network model. These analytical results give an explanation of the multi-exponentially decay pattern of the autocorrelation functions. Section 4 discusses how to fit the experiment data within the framework of the stochastic network model. The paper ends in Section 5 with a summary and some concluding remarks.

2 Modeling enzymatic reaction

2.1 The classical model and its challenge

Under the classical Michaelis-Menten model (1.1), an enzyme molecule behaves as a three-state continuous-time Markov chain with the generating matrix (infinitesimal generator)

$${\mathbf{Q}}_{MM}=\left(\begin{array}{ccc}-k_1[S]& k_1[S]& 0\\ k_{-1}& -(k_{-1}+k_2)& k_2\\ \delta & 0& -\delta \end{array}\right).$$

We can readily draw two properties from this continuous-time Markov chain model.

Proposition 2.1

The density function of the turnover time, the time that it takes the enzyme to complete one catalytic cycle (i.e., to go from state E to state E⁰), is

$$f(t)=\frac{k_1{k}_2[S]}{2p}(e^{-(q-p)t}-e^{-(q+p)t}),$$

where $p=\sqrt{{(k_1[S]+k_2+k_{-1})}^2/4-k_1{k}_2[S]}$ and q = (k₁[S] + k₂ + k₋₁)/2.

Proposition 2.2

The successive turnover times have no correlation.

The first proposition implies that the density of turnover time is almost an exponential, since the term e^−(q−p)t easily dominates the term e^−(q+p)t for most values of t; see Kou (2008b) for a proof. The second proposition is a consequence of the Markov property: each turnover time, which is a first passage time, is independently and identically distributed.

The third property concerns the autocorrelation of the fluorescence intensity. As we have seen in Figure 1, the experimentally recorded fluorescence intensity consists of high spikes and low readings. The high peaks correspond to the release of the fluorescent product (when the enzyme is at the state E⁰), whereas the low readings come from the background noise. We can thus think of the fluorescence intensity reading as a record of an on-off system: E⁰ being the on state, E and ES being the off states.

Proposition 2.3

The autocorrelation function of the fluorescence intensity is proportional to exp(−t(k₋₁ + k₂ + k₁[S])).

The proof of the proposition will be given in Corollary 3.11. This proposition says that under the Michaelis-Menten model the intensity autocorrelation decays exponentially and faster with larger substrate concentration [S].

The results from single-molecule experiment on β-gal (English et al. 2006) contradict all three properties of the Michaelis-Menten model:

1. The empirical distribution of the turnover time does not exhibit exponential decay; see Kou (2008b) for detailed explanation.

2. The experimental turnover time autocorrelations are far from zero, as seen in Figure 2.

3. The experimental intensity autocorrelations decay neither exponentially nor faster under larger concentration. See Figure 2.

2.2 A stochastic network model

We believe these contradictions are rooted in the molecule’s dynamic conformational fluctuation. An enzyme molecule is not rigid: it experiences constant changes and fluctuations in its three-dimensional shape and configuration due to the entropic and atomic forces at the nano scale (Kou and Xie, 2004; Kou 2008a). Although for a large ensemble of molecules, the (nanoscale) conformational fluctuation is buried in the macroscopic population average, for a single molecule the conformational fluctuation can be much more pronounced: different conformations could have different chemical properties, resulting in time-varying performance of the enzyme, which can be studied in the single-molecule experiment. The following stochastic network model (Kou et al. 2005a) was developed with this idea:

$$\begin{array}{cccccc}\hfill S+E_1& \underset{k_{-11}}{\overset{k_{11}[S]}{\rightleftarrows }}& {ES}_1& \stackrel{k_{21}}{\to }& \hfill P+E_1^0& E_1^0\stackrel{{\delta }_1}{\to }{E}_1\\ \hfill \downarrow \uparrow & & \downarrow \uparrow & & \hfill \downarrow \uparrow & \cdots \\ \hfill S+E_2& \underset{k_{-12}}{\overset{k_{12}[S]}{\rightleftarrows }}& {ES}_2& \stackrel{k_{22}}{\to }& \hfill P+E_2^0& E_2^0\stackrel{{\delta }_2}{\to }{E}_2\\ \hfill \cdots & & \cdots & & \hfill \cdots & \cdots \\ \hfill \downarrow \uparrow & & \downarrow \uparrow & & \hfill \downarrow \uparrow & \\ \hfill S+E_n& \underset{k_{-1n}}{\overset{k_{1n}[S]}{\rightleftarrows }}& {ES}_n& \stackrel{k_{2n}}{\to }& \hfill P+E_n^0& E_n^0\stackrel{{\delta }_n}{\to }{E}_n\end{array}.$$ (2.1)

This is still a Markov chain model but with 3n states instead of three. The enzyme still exists as a free enzyme E, an enzyme-substrate complex ES, or a returning enzyme E⁰, but it can take n different conformations indexed by subscripts in each stage. At each transition, the enzyme can either change its conformation within the same stage (such as E_i → E_j or ES_i → ES_j) or carry out one chemical step, i.e., move between the stages (such as E_i → ES_i, ES_i → E_i or ${ES}_i\to E_i^0$). Since only the product P is fluorescent in the experiment, in model (2.1) any states $E_i^0$ is an on-state, and the others are off-states. Consequently, the turnover time is the traverse time between any two on-states $E_j^0$ and $E_k^0$.

To fully specify the model, we need to stipulate the transition rates. For i ≠ j, we use α_ij, β_ij and γ_ij to denote, respectively, the transition rates of E_i → E_j, ES_i → ES_j, and $E_i^0\to E_j^0$. k_1i[S], k_−1i, k_2i and δ_i are, respectively, the transition rates of E_i → ES_i, ES_i → E_i, ${ES}_i\to E_i^0$ and $E_i^0\to E_i$. Define Q_AA, Q_BB and Q_CC to be square matrices:

$${\mathbf{Q}}_{AA}={[{\alpha }_{ij}]}_{n\times n},{\mathbf{Q}}_{BB}={[{\beta }_{ij}]}_{n\times n},{\mathbf{Q}}_{CC}={[{\gamma }_{ij}]}_{n\times n}$$

where α_ii = −Σ_{j ≠ i} α_ij, β_ii = −Σ_{j ≠ i} β_ij and γ_ii = −Σ_{j ≠ i} γ_ij. They correspond to transitions among the E_i states, among the ES_i states, and among the $E_i^0$ states, respectively. Define diagonal matrices

$$\begin{array}{l}{\mathbf{Q}}_{AB}=\text{diag}\{k_{11}[S],k_{12}[S],\cdots ,k_{1n}[S]\},{\mathbf{Q}}_{BA}=\text{diag}\{k_{-11},k_{-12},\cdots ,k_{-1n}\}\\ {\mathbf{Q}}_{BC}=\text{diag}\{k_{21},k_{22},\cdots ,k_{2n}\},{\mathbf{Q}}_{CA}=\text{diag}\{{\delta }_1,{\delta }_2,\cdots ,{\delta }_n\}.\end{array}$$ (2.2)

They correspond to transitions between the different stages. The generating matrix of model (2.1) is then

$$\mathbf{Q}=\left(\begin{array}{ccc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}& \mathbf{0}\\ {\mathbf{Q}}_{BA}& {\mathbf{Q}}_{BB}-({\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC})& {\mathbf{Q}}_{BC}\\ {\mathbf{Q}}_{CA}& \mathbf{0}& {\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}\end{array}\right)$$ (2.3)

Under this new model, the distribution of the turnover time, the correlation of turnover times and the correlation of the fluorescence intensity can be analyzed and compared with experimental data. This paper studies the autocorrelation of turnover time and the autocorrelation of fluorescence intensity.

3 Autocorrelation of turnover time and of fluorescence intensity

3.1 Dynamic equilibrium and stationary distribution

In the chemistry literature, the term “equilibrium” often refers to the state in which all the macroscopic quantities of a system are time-independent. For the microscopic system studied in single-molecule experiments, macroscopic quantities, however, are meaningless, and microscopic parameters never cease to fluctuate. Nonetheless, for a micro-system, one can talk about dynamic equilibrium in the sense that the distribution of the state quantities become time-independent, i.e., they reach the stationary distribution. The single-molecule enzyme experiment that we consider here falls into this category, since the enzymatic reactions happen quite fast. We cite the following lemma (Lemma 3.1 of Kou, 2008b), which gives the stationary distribution of the Markov chain (2.1):

Lemma 3.1

Let X(t) be the process evolving according to (2.1). Suppose all the parameters k_1i, k_−1i, k_2i, δ_i, α_ij, β_ij, and γ_ij are positive. Then X(t) is ergodic. Let the row vectors π_A = (π (E₁), π (E₂), …, π(E_n)), π_B = (π (ES₁), …, π (ES_n)), and ${\mathit{\pi }}_C=(\pi (E_1^0),\dots ,\pi (E_n^0))$ denote the stationary distribution of the entire network. Up to a normalizing constant, they are determined by

$$\begin{array}{l}{\mathit{\pi }}_A=-{\mathit{\pi }}_C{\mathbf{Q}}_{CA}\mathbf{L},{\mathit{\pi }}_B=-{\mathit{\pi }}_C{\mathbf{Q}}_{CA}\mathbf{M},\\ {\mathit{\pi }}_C({\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}-{\mathbf{Q}}_{CA}\mathbf{M}{\mathbf{Q}}_{BC})=0,\end{array}$$

where the matrices

$$\begin{array}{l}\mathbf{L}={[{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}-{\mathbf{Q}}_{AB}{({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC})}^{-1}{\mathbf{Q}}_{BA}]}^{-1},\\ \mathbf{M}={[{\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BC}-({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA}]}^{-1}.\end{array}$$

Under the stochastic network model (2.1), a turnover event can start from any state E_i and end in any $E_j^0$. It follows that the overall distribution of all the turnover times is characterized by a mixture distribution with the weights given by the stationary probability of a turnover event’s starting from E_i. The following lemma, based on Lemma 3.4 of Kou (2008b), provides the stationary probability.

Lemma 3.2

Let w be a row vector, w = (w(E₁), w(E₂), · · · w(E_n)), where w(E_i) denotes the stationary probability of a turnover event’s starting from state E_i. Then up to a normalizing constant, w is the nonzero solution of

$$\mathbf{w}(\mathbf{I}+\mathbf{M}{\mathbf{Q}}_{BC}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})=0.$$ (3.1)

3.2 Autocorrelation of turnover time

Expectation of turnover time

The enzyme turnover event occurs one after another. Each can start from any E_i and end in any $E_j^0$. The next turnover may start from E_k (k ≠ j) when the system exits the E⁰ stage from $E_k^0$. To calculate the correlation between turnover times, it is necessary to find out the probabilities of all these combinations and the expected turnover times. We introduce the following notations.

Let T_Ei and T_ESi denote the first passage time of reaching the set { $E_1^0,E_2^0,\cdots ,E_n^0$} from E_i and ES_i, respectively. Let $P_{E_i{E}_j^0}$ and $P_{{ES}_i{E}_j^0}$ be the probability that a turnover event, starting respectively from E_i and ES_i, ends in $E_j^0$. Let $P_{E_i^0{E}_j}$ denote the probability that, after the previous turnover ends in $E_i^0$, a new turnover event starts from E_j. Finally, let $T_{E_i{E}_j^0}$ and $T_{{ES}_i{E}_j^0}$ be the first passage time of reaching the state $E_j^0$ from E_i and ES_i respectively.

For the values of E(T_Ei) and E(T_ESi), we cite the following lemma (Corollary 3.3 of Kou, 2008b).

Lemma 3.3

Let the vectors μ_A = (E(T_E1), E(T_E2), …, E(T_En))^T and μ_B = (E(T_ES1), …, E(T_ESn))^T denote the mean first passage times. Then they are given by

$$\left(\begin{array}{c}{\mathit{\mu }}_A\\ {\mathit{\mu }}_B\end{array}\right)=\left(\begin{array}{c}-(\mathbf{L}+\mathbf{M})\mathbf{1}\\ -(\mathbf{N}+\mathbf{R})\mathbf{1}\end{array}\right),$$ (3.2)

where the matrices N and R are given by

$$\begin{array}{l}\mathbf{N}={[{\mathbf{Q}}_{AA}-({\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}){\mathbf{Q}}_{BA}^{-1}({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BC})]}^{-1},\\ \mathbf{R}={[{\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}-{\mathbf{Q}}_{BA}{({\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB})}^{-1}{\mathbf{Q}}_{AB}]}^{-1}.\end{array}$$

For the probabilities $P_{E_i{E}_j^0},P_{{ES}_i{E}_j^0}$ and $P_{E_i^0{E}_j}$, we have the following lemma:

Lemma 3.4

Let P_AC, P_BC and P_CA be probability matrices ${\mathbf{P}}_{AC}={[P_{E_i{E}_j^0}]}_{n\times n},{\mathbf{P}}_{BC}={[P_{{ES}_i{E}_j^0}]}_{n\times n}$ and ${\mathbf{P}}_{CA}={[P_{E_i^0{E}_j}]}_{n\times n}$. Then they are given by

$${\mathbf{P}}_{AC}=-\mathbf{M}{\mathbf{Q}}_{BC},{\mathbf{P}}_{BC}=-\mathbf{R}{\mathbf{Q}}_{BC},{\mathbf{P}}_{CA}={(\mathbf{I}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})}^{-1}.$$ (3.3)

For the expectation of $T_{E_i{E}_j^0}$ and $T_{{ES}_i{E}_j^0}$, we have

Lemma 3.5

Let ${\mathbf{E}}_{AC}={[P_{E_i{E}_j^0}E(T_{E_i{E}_j^0})]}_{n\times n}$ and ${\mathbf{E}}_{BC}={[P_{{ES}_i{E}_j^0}E(T_{{ES}_i{E}_j^0})]}_{n\times n}$ be two n × n matrices. Then they are given by

$${\mathbf{E}}_{AC}=(\mathbf{LM}+\mathbf{MR}){\mathbf{Q}}_{BC},{\mathbf{E}}_{BC}=(\mathbf{NM}+\mathbf{RR}){\mathbf{Q}}_{BC}.$$

We defer the proofs of Lemmas 3.4 and 3.5 to the Appendix.

Correlation of the turnover times

Let Tⁱ denote the ith turnover time. The next theorem, based on Lemmas 3.1 to 3.5, obtains the autocorrelation of the successive turnover times. We defer its proof to the Appendix.

Theorem 3.6

The covariance between the first turnover and the mth turnover (m > 1) is given by

$$cov(T^1,T^m)=-\mathbf{w}(\mathbf{L}+\mathbf{M}(\mathbf{I}-{\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA}))[{({\mathbf{P}}_{AC}{\mathbf{P}}_{CA})}^{m-1}-\mathbf{1}\mathbf{w}]{\mathit{\mu }}_A,$$

where ${\mathbf{P}}_{AC}{\mathbf{P}}_{CA}=-\mathbf{M}{\mathbf{Q}}_{BC}{(\mathbf{I}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})}^{-1}$.

The matrix P_ACP_CA is the product of two transition-probability matrices, so it is a stochastic matrix. Given that all the states in the stochastic network model communicate with each other, P_ACP_CA is also irreducible, and all its entries are positive. According to the Perron-Frobenius theorem (Horn and Johnson, 1985), such matrix has eigenvalue one with simplicity one, and the absolute values of the other eigenvalues are strictly less than one. We therefore obtain the following corollary of Theorem 3.6.

Corollary 3.7

Suppose that P_ACP_CA is diagonalizable:

$${\mathbf{P}}_{AC}{\mathbf{P}}_{CA}=\mathbf{U}\mathit{\lambda }{\mathbf{U}}^{-1}=\mathbf{1}\mathbf{w}+\sum _{l=2}^n{\lambda }_l{\varphi }_l{\psi }_l^T,$$

where the diagonal matrix λ = diag(1, γ₂, · · ·, γ_n) consists of the eigenvalues of P_ACP_CA with |λ_i| < 1; the columns, 1, ϕ₂, · · ·, ϕ_n, of matrix U are the corresponding right eigenvectors; and the rows, w, ψ₂, · · ·, ψ_n, of U⁻¹ are the corresponding left eigenvectors. Then we have

$$cov(T^1,T^m)=\sum _{i=2}^n{\sigma }_i{\lambda }_i^{m-1},$$ (3.4)

where ${\sigma }_i=-\mathbf{w}(\mathbf{L}+\mathbf{M}(\mathbf{I}-{\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA})){\varphi }_i{\psi }_i^T{\mathit{\mu }}_A$.

Although the matrix P_ACP_CA may have complex eigenvalues, these complex eigenvalues and corresponding eigenvectors always appear as conjugate pairs so that the imaginary parts in equation (3.4) cancel each other. As a result, we could treat all λ_i and σ_i as if they were real numbers.

Theorem 3.6, along with Corollary 3.7, provides an explanation of why the correlation of turnover times is not zero. At first sight, it seems to contradict the memoryless property of a Markov chain. What actually happens is that the state must be explicitly specified for the memoryless property to hold (i.e., one needs to exactly specify whether an enzyme is at state E₁ or E₂), whereas in the single-molecule experiment we only know whether the system is in an ‘on’ or ‘off’ state (for example, one only knows that the enzyme is in one of the on-states $E_1^0,\dots E_n^0$). When there are multiple states, this aggregation effect leads to incomplete information that prevents the independence between successive turnovers; consequently, each turnover time carries some information about its reaction path, which is correlated with the reaction path of the next turnover, resulting in the correlation between successive turnover times.

Corollary 3.7 also states that since |λ_i| < 1, the autocorrelation is a mixture of exponential decays. Thus, depending on the relative scales of the eigenvalues, the actually decay might be single-exponential when one eigenvalue dominates the others or multi-exponential when several major eigenvalues jointly contribute to the decay.

Fast Enzyme Reset

In most enzymatic reactions, including the one we study, the enzyme returns very quickly to restart a new cycle once the product is released (Segel 1975). Those enzymes are called fast-cycle-reset enzymes. To model this fact, we let δ_i (i = 1, 2 · · ·, n), the transition rate from $E_i^0$ to E_i, go to infinity. Then any enzyme in state $E_i^0$ will always return to state E_i instantly, and the related transition probability matrix P_CA, defined in equation (3.3), becomes the identity matrix.

3.3 Autocorrelation of fluorescence intensity

Correlation of intensity as a function of time

In the single-enzyme experiments, the raw data are the time traces of fluorescence intensity, as shown in Figure 1. The time lag between two adjacent high fluorescence spikes gives the enzymatic turnover time. The fluorescence intensity reading, however, is subject to detection error: the error caused by the limited time resolution Δt of the detector. Starting from time 0, the detector will only record intensity data at multiples of Δt: 0, Δt, 2Δt, …, kΔ_t, …. The intensity reading at time kΔt is actually the total number of photons received during the period of ((k − 1) Δt, kΔt). Thus, the detection errors of turnover time is roughly Δt. When the successive reactions occur slowly, the average turnover time is much longer than Δt, and the error is negligible. But when the reactions happen very frequently, the average turnover time becomes comparable to Δt, and this error cannot be ignored. In fact, when the substrate concentration is high enough, the enzyme will reach the ‘on’ states so frequently that most of the intensity readings are very high, making it impossible to reliably determine the individual turnover times. Under this situation, it is necessary to directly study the behavior of the raw intensity reading.

There are two main sources of the photons generated in the experiment: the weak but perpetual background noise and the strong but short-lived burst. The number of photons received from two different sources can be modeled as two independent Poisson processes with different rates. We can use the following equation to represent I(t), the intensity recorded at time t,

$$I(t)=N_t(T_{on}(t))+N_t^0(\mathrm{\Delta }t),$$ (3.5)

where N_t(s) and $N_t^0(s)$ represent the total number of photons received due to the burst and background noise, respectively, within a length s sub-interval of (t − Δt, t); T_on(t) is the total time that the enzyme system spends at the ‘on’ states (any $E_i^0$) within the time interval (t − Δt, t). N_t(s) and $N_t^0(s)$ are independent Poisson processes with rates ν and ν₀ respectively. With this representation, we have the following theorem, whose proof is deferred to the Appendix.

Theorem 3.8

The covariance of the fluorescence intensity is

$$cov(I(0),I(t))\propto \sum _{i=2}^{3n}{C}_i{e}^{{\mu }_i(t-\mathrm{\Delta }t)},$$ (3.6)

where μ_i are the non-zero eigenvalues of the generating matrix Q defined in equation (2.3), and C_i are constants only depending on Q.

Since −Q is a semi-stable matrix (Horn and Johnson 1985), it follows that the real parts of all μ_k (k > 1) are negative. For a real matrix, the complex eigenvalues along with their eigenvectors always appear in conjugate pairs; thus, the imaginary parts cancel each other in (3.6) and only the real parts are left. Therefore, we known according to Theorem 3.8 that the covariance of intensity will decay multi-exponentially.

Fast enzyme reset and intensity autocorrelation

A fast-cycle-reset enzyme jumps from state $E_i^0$ to E_i with little delay. A short burst of photons is released during the enzyme’s short stay at $E_i^0$. For fast-cycle-reset enzymes, the behavior of the whole system can be well approximated by an alternative system, where only states E_i and ES_i (i ∈ 1, 2, · · ·, n) exist: the transition rates among the E’s, among the ES’s, and from E_i to ES_i are exactly the same as in the original system, but the transition rate from ES_i to E_i is changed from k_−1i to k_−1i + k_2i, since once a transition of ${ES}_i\to E_i^0$ occurs, the enzyme quickly moves to E_i. We can thus think of lumping $E_i^0$ and E_i together to form the alternative system, which has generating matrix

$$\mathbf{K}=\left(\begin{array}{cc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}\\ {\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC}& {\mathbf{Q}}_{BB}-({\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC})\end{array}\right).$$ (3.7)

K is also a negative semi-stable matrix with 2n eigenvalues, one of which is zero. The following theorem details how well the eigenvalues of K approximate those of Q.

Theorem 3.9

Assume Q_CA = δdiag{q₁, · · ·, q_n}, where q₁, · · ·, q_n are fixed constants, while δ is large. Let κ_i (i = 2, 3, · · ·, 2n) denote the non-zero eigenvalues of K, then for each κ_i, there exists an eigenvalue μ_i of Q such that

$$\mid {\mu }_i-{\kappa }_i\mid =O({\delta }^{-1/2}).$$

The rest n eigenvalues of Q satisfy

$$\mid {\mu }_i+\delta q_{i-2n}\mid =O(1),i=2n+1,\dots ,3n.$$

The proof is deferred to the Appendix. This theorem says that for fast-cycle-reset enzymes with large δ, the first 2n − 1 non-zero eigenvalues of Q can be approximated by the eigenvalues of K, while the other n eigenvalues μ_2n+1, …, μ_3n of Q are of the same order of δ. Since all the eigenvalues have negative real parts, according to equation (3.6), the terms associated with μ_2n+1, …, μ_3n decay much faster so their contribution can be ignored. Thus, we have the following results for the intensity autocorrelation.

Corollary 3.10

For fast-cycle-reset enzymes (δ → ∞),

$$cov(I(0),I(t))\propto \sum _{i=2}^{2n}{C}_i{e}^{{\kappa }_i(t-\mathrm{\Delta }t)}$$

where κ_i are the non-zero eigenvalues of matrix K defined in equation (3.7).

Corollary 3.11

For the classic Michaelis-Menten model, where n = 1,

$$\mathbf{K}=\left(\begin{array}{cc}-k_1[S]& k_1[S]\\ k_2+k_{-1}& -k_2-k_{-1}\end{array}\right).$$

The only non-zero eigenvalue is −(k₋₁ + k₂ + k₁[S]). We thus have, for fast-cycle-reset enzymes,

$$cov(I(0),I(t))\propto e^{-(k_{-1}+k_2+k_1[S])(t-\mathrm{\Delta }t)}.$$

4 From theory to data

We have shown in the preceding sections that the autocorrelation of turnover times and the correlation of intensity follow

$$cov(T^1,T^m)\propto \sum {\lambda }_i^{m-1}{\sigma }_i,cov(I(0),T(t))\propto \sum e^{{\kappa }_i(t-\mathrm{\Delta }t)}{C}_i.$$

Before applying these equations to fit the experimental data, the following problems must be addressed. First, we know so far that the decay patterns must be multi-exponential, but we do not yet know how the eigenvalues are related to the rate constants (k_1i, k_−1i, k_2i, etc.) and the substrate concentration [S], which is the only adjustable parameter in the experiment. Second, we do not know the expressions of the coefficients (σ_i and C_i). Third, we do not know the number of distinct conformations n. We only know that it must be large: each enzyme consists of hundreds of vibrating atoms, and as a whole, it expands and rotates in the 3-dimensional space within the constraint of chemical bonds. We next address these questions before fitting the experimental data.

4.1 Eigenvalues as functions of rate constants and substrate concentration

In the enzyme experiments, the transition rates are intrinsic properties of the enzyme and the enzyme-substrate complex; they are not subject to experimental control. The only variable subject to experimental control is the concentration of the substrate molecules [S]. The higher the concentration, the more likely that the enzyme molecule could bind with a substrate molecule to form a complex. This is why the association rate k_1i[S] (the rate of E_i → ES_i) is proportional to the concentration. The experiments were repeated under different concentrations, resulting in different decay patterns of the autocorrelation functions as in Figure 2. A successful theory should be able to explain the relationship between concentration and autocorrelation decay pattern.

The concentration only affect the transition rates between E_i and ES_i, which are denoted by Q_AB in equation (2.2). Define Q̃_AB = diag{k_1i, k_2i, · · ·, k_ni}, which is independent of [S]; then Q_AB = [S]Q̃_AB.

Four scenarios for simplication

To delineate the relationship between [S] and the autocorrelation decay pattern, we next simplify the generating matrices. Below are four scenarios that we will consider. Each of the scenarios guarantees the classical Michaelis-Menten equation, a hyperbolic relationship between the reaction rate and the substrate concentration,

$$v=\frac{1}{E(T)}=\frac{1}{\mathbf{w}{\mathit{\mu }}_A}\propto \frac{[S]}{[S]+C}\text{with}\text{some}\text{constant}C,$$ (4.1)

which was observed in both the traditional and single-molecule enzyme experiments (see Kou et al. 2005a, English et al. 2006, and Kou 2008b for detailed discussion). Each scenario has its own biochemical implications.

• Scenario 1. There are no or negligible transitions among the E_i states, that is α_ij → 0 for i ≠ j.

• Scenario 2. There are no or negligible transitions among the ES_i states, that is β_ij → 0 for i ≠ j.

  Scenarios 1 and 2 correspond to the so-called slow fluctuating enzymes (whose conformation fluctuates slowly over time).

• Scenario 3. The transitions among the E_i states are much faster than the others; that is, Q_AA = τQ̃_AA and the scale τ ≫ 1 is much larger than other transition rates.

• Scenario 4. The transitions among the ES_i states are much faster than the others; that is, Q_BB = τQ̃_BB and the scale τ ≫ 1 is much larger than other transition rates.

  Scenarios 3 and 4 correspond to the so-called fast fluctuating enzymes (whose conformations fluctuate fast).

Remark

In the previous work (Kou 2008b), there are two other scenarios, which can also give rise to the hyperbolic relationship (4.1): primitive enzymes, whose dissociate rate is much larger than their catalytic rate (Albery and Knowles 1976; Min et al. 2006; Min et al. 2005a), and conformational-equilibrium enzymes, whose energy-barrier difference between dissociation and catalysis is invariant across conformations (Min et al. 2006). But our analysis based on those two scenarios does not lead to any meaningful conclusion, so we omit them here.

The effect of concentration on turnover time autocorrelation

Based on the four scenarios, we have the following theorem for autocorrelation of turnover times.

Theorem 4.1

For enzymes with fast cycle reset, the transition probability matrix governing the autocorrelation of turnover times is

$${\mathbf{P}}_{AC}{\mathbf{P}}_{CA}=-\mathbf{M}{\mathbf{Q}}_{BC}{(\mathbf{I}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})}^{-1}=-\mathbf{M}{\mathbf{Q}}_{BC}.$$

Its eigenvalues λ_i, under the four different scenarios, satisfy:

• Scenario 1. λ_i do not depend on [S], the substrate concentration. Thus, the autocorrelation decay should be similar for all concentrations.

• Scenario 2. λ_i depend on [S] hyperbolically. More precisely, if we use λ_i([S]) (i = 1, 2, …, n) to emphasize the dependence of the eigenvalues on [S], we have

  $${\lambda }_i([S])=\frac{1}{1-(1-{\lambda }_i^{-1}(1))/[S]}$$

  Thus the autocorrelation decay should be slower under larger concentration.

• Scenario 3 or Scenario 4. The non-one eigenvalues are of order τ⁻¹, so the autocorrelation should decay extremely fast for all concentrations.

This theorem tells us that for fast fluctuation enzymes (Scenario 3 or 4), the turnover time correlation tends to be zero. Intuitively, this is because the fast fluctuation enzymes prefer conformation fluctuation rather than going through the binding-association-catalytic path that leads to the product, so in a single turnover event, the enzyme undergoes intensive conformation changes, which effectively blurs the information on the reaction path carried by the turnover time, resulting in zero correlation. Under Scenario 1, the autocorrelation decay pattern does not vary when the concentration changes. This is because when the enzyme does not fluctuate, it goes from E_i to ES_i directly, and the change of concentration consequently does not alter the distribution of reaction path. Thus, the correlation between turnover times does not depend on the concentration.

The result from Scenario 1, 3 or 4 contradicts the experimental finding: correlation exists between the turnover time and is stronger under higher concentration (see Figure 2). Only Scenario 2 fully agrees with the experiments, suggesting that the enzyme-substrate complex (ES_i) does not fluctuate much. This is supported by recent single-molecule experimental findings (Lu et al. 1998; Yang et al. 2003; Min et al. 2005b), where slow conformational fluctuation in the enzyme-substrate complexes were observed.

The effect of concentration on fluorescence intensity autocorrelation

We now consider the intensity autocorrelation under each of the four scenarios. We write Q_AA = I_α + J_α, where I_α = diag{α₁₁, · · ·, α_nn}, and Q_BB = I_β + J_β, where I_β = diag{β₁₁, · · ·, β_nn}. For Scenarios 1 and 2, we assume that both the enzyme and the enzyme-substrate complex fluctuate slowly: α_ij and β_ij (i ≠ j) are negligible but the sums α_ii = −Σ_{j ≠ i} α_ij and β_ii = −Σ_{j ≠ i} β_ij are not. Furthermore, we assume that in Scenario 1 the enzyme fluctuation is much slower than the enzyme-substrate complex fluctuation (so Q_AA = 0 and Q_BB = I_β in Scenario 1), and in Scenario 2 the enzyme-substrate complex fluctuation is much slower (so Q_BB = 0 and Q_AA = I_α Scenario 2).

Theorem 4.2

For enzymes with fast cycle reset, the matrix governing the intensity autocorrelation is K. Its eigenvalues and the autocorrelation decay, under the four different scenarios, satisfy:

• Scenario 1 (Q_AA = 0 and Q_BB = I_β). The autocorrelation decay is slower under lower concentration, and the dominating eigenvalues are given by

  $${\kappa }_i=\frac{1}{2}\left(-([S]k_{1i}-{\beta }_{ii}+k_{-1i}+k_{2i})+\sqrt{{([S]k_{1i}-{\beta }_{ii}+k_{-1i}+k_{2i})}^2+4{\beta }_{ii}[S]k_{1i}}\right)$$
• Scenario 2 (Q_BB = 0 and Q_AA = I_α). The autocorrelation decay is faster under lower concentration, and the dominating eigenvalues are given by

  $${\kappa }_i=\frac{1}{2}\left(-([S]k_{1i}-{\alpha }_{ii}+k_{-1i}+k_{2i})+\sqrt{{([S]k_{1i}-{\alpha }_{ii}+k_{-1i}+k_{2i})}^2+4{\alpha }_{ii}(k_{-1i}+k_{2i})}\right)$$

• Scenario 3.The autocorrelation decay does not depend on the concentration.

• Scenario 4. The autocorrelation decay is slower under lower concentration.

The proof of the theorem is given in the Appendix. Our results of the dependence of turnover time autocorrelation and fluorescence intensity autocorrelation on the substrate concentration show that in order to have slower decay under higher substrate concentration (as seen in Figure 2), fluctuation of both the enzyme and the enzyme-substrate complex cannot be fast; furthermore, the fluctuation of the enzyme-substrate complex needs to be slower than the fluctuation of the enzyme.

In summary, each of the four scenarios yields different autocorrelation pattern, but only the one under Scenario 2 matches the experimental finding. Therefore, we will focus on Scenario 2 from now on.

4.2 Continuous limit

To simplify the coefficients σ_i and C_i and to address the number of distinct conformations n, we adopt the idea in the previous work (Kou et al. 2005a, Kou 2008b) by utilizing a continuous limit. First, we let n → ∞ and in this way model the transition rates as continuous variables with certain distributions. Consequently, we treat the eigenvalues also as continuous variables. Second, we assume that all the coefficients (σ_i and C_i) are proportional to the probability weight of the conjugate eigenvalues. This assumption is partly based on the fact that all the observed experimental correlation are positive. With these two assumptions, the covariance can be represented by

$$cov(T^1,T^m)\propto \int {\lambda }^{m}f(\lambda )d\lambda ,cov(I(0),I(t))\propto \int e^{\kappa (t-\mathrm{\Delta }t)}g(\kappa )d\kappa ,$$

where f and g are the corresponding distribution functions.

λ and κ are functions of the transition rates. Since the transition rates are always positive, a natural choice is to model the transition rates as either constants or following Gamma distributions. In the previous work (Kou, 2008b) on the stochastic network model, the association rate k₁ and dissociation rate k₋₁ are modeled as constants while the catalytic rate k₂ follows a Gamma distribution Γ(a, b). We adopt them in our fitting.

We know from Section 4.1 that Scenario 2 matches the experimental finding, so we take Q_BB = 0 and Q_AA = I_α. Then the eigenvalue λ (based on Theorem 4.1 and its proof in the Appendix) is given by

$$\lambda =\frac{1}{1+{\alpha }^{\ast }(k_{-1}+k_2)/([S]k_1{k}_2)},$$ (4.2)

and the eigenvalue κ (based on Theorem 4.2) is

$$\kappa =\frac{1}{2}\left(-([S]k_1+{\alpha }^{\ast }+k_{-1}+k_2)+\sqrt{{([S]k_1+{\alpha }^{\ast }+k_{-1}+k_2)}^2-4{\alpha }^{\ast }(k_{-1}+k_2)}\right),$$ (4.3)

where α^* stands for a generic −α_ii (since we are taking the continuous version). For the distribution of α^* (i.e., the distribution of −α_ii), we note that first, its support should be the positive real line, and second, −α_ii = Σ_{j ≠ i} α_ij is a sum of many random variables α_ij from a common distribution, so we expect that the distribution of α^* should be infinitely divisible. These two considerations lead us to assume a Gamma distribution Γ(a_α, b_α) for α^*.

4.3 Data fitting

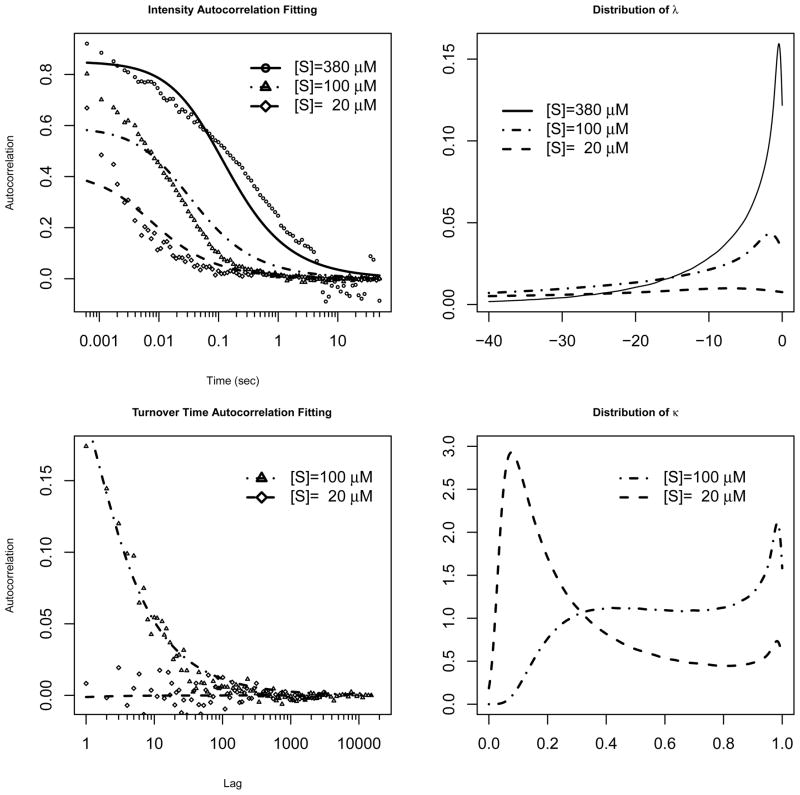
The data available to us include the intensity correlation under three concentrations: [S] = 380, 100 and 20 μM (micro molar), and turnover time autocorrelation under two concentrations [S] = 100 and 20 μM. We calculated eigenvalues based on equations (4.2) and (4.3), where k₁ and k₋₁ are constants, α^* and k₂ follow distributions Γ(a_α, b_α) and Γ(a, b), respectively. The parameters of interests are k₁, k₋₁, a, b, a_αand b_α. The best fits are found through minimizing the square distance between the theoretical and observed values. The parameters are estimated as: k₁ = 1.785 × 10³(μM)⁻¹s⁻¹, k₋₁ = 6.170 × 10³s⁻¹, a = 13.49, b = 2.279s⁻¹, a_α = 0.6489, and b_α = 1.461 × 10³s⁻¹ (s stands for second). Figures 3 shows the fitting of the autocorrelation functions and the distributions of the eigenvalues.

Figure 3.

Left: Data fitting to the intensity and turnover time autocorrelations based on equations (4.2) and (4.3). Right: The corresponding distributions of the eigenvalues λ and κ.

Figure 3 shows that our model gives a good fit to the turnover time autocorrelation and an adequate fit to the fluorescence intensity autocorrelation, capturing the main trend in the intensity autocorrelation. The distributions of the eigenvalues in the right panels clearly indicate that higher substrate concentration corresponds to larger eigenvalues, which are then responsible for the slower decay of the autocorrelations.

Our model thus offers an adequate explanation of the observed decay patterns of the autocorrelation functions. The stochastic network model tells us why the decay must be multi-exponential. It further explains why the decay is slower under higher substrate concentration. Our consideration of the different scenarios also provides insight on the enzyme’s conformational fluctuation: slow fluctuation, particularly of the enzyme-substrate complex, gives rise to the experimentally observed autocorrelation decay pattern.

5 Discussion

In this article we explored the stochastic network model previously developed to account for the empirical puzzles arising from recent single-molecule enzyme experiments. We conducted a detailed study of the autocorrelation function of the turnover time and of the fluorescence intensity and investigate the effect of substrate concentration on the correlations.

Our analytical results show that (a) the stochastic network model gives multi-exponential autocorrelation decay of both the turnover times and the fluorescence intensity, agreeing with the experimental observation; (b) under suitable conditions, the autocorrelation decays more slowly with higher concentration, also agreeing with the experimental result; (c) the slower autocorrelation decay under higher concentration implies that the fluctuation of the enzyme-substrate complex should be slow, corroborating the conclusion from other single-molecule experiments (Lu et al. 1998; Yang et al. 2003; Min et al. 2005b). In addition to providing a theoretical underpinning of the experimental observations, the numerical result from the model fits well with the experimental autocorrelation as seen in Section 4.

Some problems remain open for future investigation:

1. When we discussed the dependence of intensity autocorrelation on substrate concentration in Section 4.1, we approximated the fluctuation transition matrix with its diagonal entries. This simple approximation provides useful insight into the decay pattern under different concentration. A better approximation that goes beyond the diagonal entries is desirable. It might lead to a better fitting to the experimental data.

2. We used Gamma distribution to model the transition rates. This is purely statistical. Can it be derived from a physical angle? If so, the connection not only will lead to better estimation, but also provides new insight into the underlying mechanism of enzyme’s conformation fluctuation.

3. We used the continuous limit n → ∞ to do the data fitting so that the number of parameters reduces from more than 3n to a manageable six. Obtaining the standard error for the estimates is open for future investigation. The main difficulties are the lack of tractable tools to approximate the standard error of the autocorrelation estimates and the challenge to carry out a Monte Carlo estimate (n needs to be quite large for an ad hoc Monte Carlo simulation, but such an n will bring back a large number of unspecified parameters).

Single-molecule biophysics, like many newly emerging fields, is interdisciplinary. It lies at the intersection of biology, chemistry and physics. Owing to the stochastic nature of the nano world, single-molecule biophysics also presents statisticians with new problems and new challenges. The stochastic model for single-enzyme reaction represents only one such case among many interesting opportunities. We hope this articles would generate further interests in solving biophysical problems with modern statistical methods; and we believe that the knowledge and tools gained in this process will in turn advance the development of statistics and probability.

Appendix: Proofs

PROOF of Lemma 3.4

Using the first-step analysis, we have

$$\mathbf{G}\left(\begin{array}{c}{\mathbf{P}}_{AC}\\ {\mathbf{P}}_{BC}\end{array}\right)=-\left(\begin{array}{c}\mathbf{0}\\ {\mathbf{Q}}_{BC}\end{array}\right),$$

where

$$\mathbf{G}=\left(\begin{array}{cc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}\\ {\mathbf{Q}}_{BA}& {\mathbf{Q}}_{BB}-({\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC})\end{array}\right)={\left(\begin{array}{cc}\mathbf{L}& \mathbf{M}\\ \mathbf{N}& \mathbf{R}\end{array}\right)}^{-1}.$$

Only the diagonal elements of G are negative, and its row sums are either 0 or negative. Thus, −G is a stable matrix (Horn and Johnson, 1985), which always has a inverse. Thus, we have:

$$\left(\begin{array}{c}{\mathbf{P}}_{AC}\\ {\mathbf{P}}_{BC}\end{array}\right)=-{\mathbf{G}}^{-1}\left(\begin{array}{c}\mathbf{0}\\ {\mathbf{Q}}_{BC}\end{array}\right)=\left(\begin{array}{c}-\mathbf{M}{\mathbf{Q}}_{BC}\\ -\mathbf{R}{\mathbf{Q}}_{BC}\end{array}\right).$$

For $P_{E_i^0{E}_j}$, similarly, we have

$${\mathbf{P}}_{CA}=-{({\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA})}^{-1}{\mathbf{Q}}_{CA}={(\mathbf{I}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})}^{-1}.$$

PROOF of Lemma 3.5

For $E(T_{E_i{E}_j^0})$, when the first-step analysis is applied, the first-step probability should be conditioned on the exit state $E_j^0$, i.e. $P(E_i\text{returns}\text{to}{E}_k\text{first}\mid \text{exit}\text{at}{E}_j^0)=P(E_i\text{returns}\text{to}{E}_k\text{first})P_{E_k{E}_j^0}/P_{E_i{E}_j^0}$. Thus, we have the following equation

$$E(T_{E_i{E}_j^0})=\left(1+k_{1i}[S]\frac{P_{{ES}_i{E}_j^0}}{P_{E_i{E}_j^0}}E(T_{{ES}_i{E}_j^0})+\sum _{k\ne i}{\alpha }_{ik}\frac{P_{E_k{E}_j^0}}{P_{E_i{E}_j^0}}E(T_{E_k{E}_j^0})\right)/\left(k_{1i}[S]+\sum _{k\ne i}{\alpha }_{ik}\right).$$

Similar expression can be derived for $E(T_{{ES}_i{E}_j^0})$. Together we have

$$\left(\begin{array}{c}{\mathbf{E}}_{AC}\\ {\mathbf{E}}_{BC}\end{array}\right)=-{\mathbf{G}}^{-1}\left(\begin{array}{c}{\mathbf{P}}_{AC}\\ {\mathbf{P}}_{BC}\end{array}\right)=\left(\begin{array}{c}\mathbf{LM}{\mathbf{Q}}_{BC}+\mathbf{MR}{\mathbf{Q}}_{BC}\\ \mathbf{NM}{\mathbf{Q}}_{BC}+\mathbf{RR}{\mathbf{Q}}_{BC}\end{array}\right).$$

PROOF of Theorem 3.6

cov(T¹, T^m) = E(T¹T^m) − E(T¹)E(T^m). The first term E(T¹T^m) can be expressed as

$$E(T^1{T}^m)=\sum _{i,j,k,l}w(E_i)P_{E_i{E}_j^0}E(T_{E_i{E}_j^0})P_{E_j^0{E}_k}{P}_{E_k{E}_l}^{(m-2)}E(T_{E_l}),$$

that is, the system starts the first turnover event from E_i, ends it in $E_j^0$, then starts the second from E_k, repeats this procedure for m − 2 times, and finally starts the last turnover from E_l. Note that ${[P_{E_k{E}_l}^{(m-2)}]}_{n\times n}={({\mathbf{P}}_{AC}{\mathbf{P}}_{CA})}^{m-2}$. Thus, using the matrices defined in Lemmas 3.1 to 3.5, we have

$$cov(T^1,T^m)=\mathbf{w}{\mathbf{E}}_{AC}{\mathbf{P}}_{CA}{({\mathbf{P}}_{AC}{\mathbf{P}}_{CA})}^{m-2}{\mathit{\mu }}_A-{(\mathbf{w}{\mathit{\mu }}_A)}^2.$$

Applying the results of Lemmas 3.4 and 3.5 and the facts that $\mathbf{R}=(\mathbf{I}-{\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA})\mathbf{M}$ and ${(\mathbf{w}{\mathit{\mu }}_A)}^2=-\mathbf{w}(\mathbf{L}+\mathbf{M})\mathbf{1}\mathbf{w}{\mathit{\mu }}_A=-\mathbf{w}(\mathbf{L}+\mathbf{M}(\mathbf{I}-{\mathbf{Q}}_{\mathbf{AB}}^{-\mathbf{1}}{\mathbf{Q}}_{\mathbf{AA}}))\mathbf{1}\mathbf{w}{\mathit{\mu }}_A$, we can finally arrange the covariance as

$$cov(T^1,T^m)=-\mathbf{w}(\mathbf{L}+\mathbf{M}(\mathbf{I}-{\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA}))[{({\mathbf{P}}_{AC}{\mathbf{P}}_{CA})}^{m-1}-\mathbf{1}\mathbf{w}]{\mathit{\mu }}_A.$$

PROOF of Corollary 3.7

We only need to prove that 1 and w are, respectively, the right and left eigenvectors of P_ACP_CA associated with the eigenvalue 1. The first is a direct consequence of the fact that P_ACP_CA is a stochastic matrix. The second can be verified by observing that $-\mathbf{wM}{\mathbf{Q}}_{BC}{(\mathbf{I}-{\mathbf{Q}}_{CA}^{-1}{\mathbf{Q}}_{CC})}^{-1}=\mathbf{w}$ through equation (3.1).

PROOF of Theorem 3.8

In equation (3.5), the second term $N_t^0(\mathrm{\Delta }t)$ represents the independent white noise during period (t − Δt, t). Thus,

$$\begin{array}{l}cov(I(0),I(t))=E[N_t(T_{on}(t))N_0(T_{on}(0))]-E[N_t(T_{on}(t))]E[N_0(T_{on}(0))]\\ ={\nu }^2[E(T_{on}(t)T_{on}(0))-E(T_{on}(t))E(T_{on}(0))]\end{array}$$

Let $\mathcal{S}=\{E_1,\cdots ,E_n,{ES}_1,\cdots ,{ES}_n,E_1^0,\cdots ,E_n^0\}$ be the set of all possible states. Let X_t be the process evolving according to (2.1). Let π_i be the equilibrium probability of state i and P_ij(s) be the transition probability from state i to state j after time s. We have

$$\begin{array}{l}E(T_{on}(t)T_{on}(0))-E(T_{on}(t))E(T_{on}(0))\\ =\sum _{i,j,k,l\in \mathcal{S}}{\pi }_i{P}_{ij}(\mathrm{\Delta }t)P_{jk}(t-\mathrm{\Delta }t)P_{kl}(\mathrm{\Delta }t)E(T_{on}(0)\mid X_{-\mathrm{\Delta }t}=i,X_0=j)E(T_{on}(t)\mid X_{t-\mathrm{\Delta }t}=k,X_t=l)\\ -\sum _{i,j,k,l\in \mathcal{S}}{\pi }_i{P}_{ij}(\mathrm{\Delta }t){\pi }_k{P}_{kl}(\mathrm{\Delta }t)E(T_{on}(0)\mid X_{-\mathrm{\Delta }t}=i,X_0=j)E(T_{on}(t)\mid X_{t-\mathrm{\Delta }t}=k,X_t=l)\\ =\sum _{i,j,k,l\in \mathcal{S}}{\pi }_i{P}_{ij}(\mathrm{\Delta }t)P_{kl}(\mathrm{\Delta }t)E(T_{on}(0)\mid X_{-\mathrm{\Delta }t}=i,X_0=j)\\ \times E(T_{on}(t)\mid X_{t-\mathrm{\Delta }t}=k,X_t=l)\{P_{jk}(t-\mathrm{\Delta }t)-{\pi }_k\}\end{array}$$

The probability transition matrix [P_ij(t)]_3n×3n is the matrix exponential of the generating matrix (2.1): [P_ij(t)]_3n×3n = exp(Qt). Zero is an eigenvalue of Q with right eigenvector 1 and left eigenvector π, the stationary distribution. Assume Q is diagonalizable. Let μ_i, i = 2, 3 · · ·, 3n, denote the other eigenvalues, and ξ_i and ${\mathit{\eta }}_i^T$ be the corresponding right and left eigenvectors. We have

$$exp(\mathbf{Q}t)=\mathbf{1}\mathit{\pi }+\sum _{i=2}^{3n}{e}^{{\mu }_{i}t}{\mathit{\xi }}_i{\mathit{\eta }}_i^T.$$

Therefore, we can rewrite

$$cov(I(0),I(t))\propto \sum _{i=2}^{3n}{C}_i{e}^{{\mu }_i(t-\mathrm{\Delta }t)}.$$

To prove Theorem 3.9, we need the following two useful lemmas on the eigenvalues of a matrix.

Lemma A.1

(Theorems 6.1.1 and 6.4.1 of Horn and Johnson (1985)) Let A = [a_ij] ∈ M_n, where M_n is the set of all complex matrices. Let α ∈ [0, 1] be given and define $R_i^{\prime }$ and $C_i^{\prime }$ as the deleted row and column sums of A, respectively,

$$R_i^{\prime }=\sum _{j=1,j\ne i}\mid a_{ij}\mid ,C_i^{\prime }=\sum _{j=1,j\ne i}\mid a_{ji}\mid .$$

Then, (1) all the eigenvalues of A are located in the union of n discs

$$\underset{i=1}{\overset{n}{\cup }}\{z\in \mathbf{C}:\mid z-a_{ii}\mid \le R_i^{\prime \alpha }{C}_i^{\prime 1-\alpha }\}.$$ (A.1)

(2) Furthermore, if a union of k of these n discs forms a connected region that is disjoint from all the remaining n − k discs, then there are precisely k eigenvalues of A in this region.

Lemma A.2

(p 63–67, Wilkinson (1965)) Let A and B be matrices with elements satisfying |a_ij| < 1, |b_ij| < 1. If λ₁ is a simple eigenvalue (i.e., an eigenvalue with multiplicity 1) of A, then for matrix A + εB, where ε is sufficiently small, there will be a eigenvalue λ₁(ε) of A + εB such that

$$\mid {\lambda }_1(\epsilon )-{\lambda }_1\mid =O(\epsilon ).$$

Furthermore, if we know that one eigenvector of A associated with λ₁ is x₁, then there is an eigenvector x₁(ε) of A + εB associated with λ₁(ε) such that

$$\mid {\mathit{x}}_{\mathbf{1}}(\mathit{\epsilon })-{\mathit{x}}_{\mathbf{1}}\mid =O(\epsilon ).$$

Note that since dividing a matrix by a constant only changes the eigenvalues with the same proportion, the condition that the entries of A and B are bounded by 1 can be relaxed to that the entries of A and B are bounded by a finite positive number.

PROOF of Theorem 3.9

According to Lemma A.1, all the eigenvalues of Q must lie in the union of discs centered at Q_ii with radii defined by (A.1). If we take α = 1/2 in (A.1), then the first n discs corresponding to the diagonal entries of Q_AA − Q_AB have centers O(1) and radii O(δ^1/2); the second n discs corresponding to the diagonal entries of Q_BB − Q_BC − Q_BA have centers O(1) and radii O(1); the third n discs corresponding to the diagonal entries of Q_CC − Q_CA have centers O(δ) and radii O(δ^1/2). Thus, for δ large enough, the union of the first 2n discs does not overlap with the union of the last n discs, so we know from Lemma A.1 that Q has 2n eigenvalues with order O(δ^1/2) in the union of the first 2n discs and n other eigenvalues with order O(δ) in the union of the last n discs.

For the n eigenvalues with order O(δ), consider the following two matrices

$$\mathbf{Y}=\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \frac{1}{\delta }{\mathbf{Q}}_{CA}& \mathbf{0}& -\frac{1}{\delta }{\mathbf{Q}}_{CA}\end{array}\right],\mathbf{Z}=\left[\begin{array}{ccc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}& \mathbf{0}\\ {\mathbf{Q}}_{BA}& {\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}& {\mathbf{Q}}_{BC}\\ \mathbf{0}& \mathbf{0}& {\mathbf{Q}}_{CC}\end{array}\right].$$

We have $\frac{1}{\delta }\mathbf{Q}=\mathbf{Y}+\frac{1}{\delta }\mathbf{Z}$. Zero is an eigenvalue of Y with multiplicity 2n, and the other n eigenvalues of Y are −q₁, −q₂, …, −q_n. For large δ, according to Lemma A.2, there exists n eigenvalues of $\frac{1}{\delta }\mathbf{Q}$ that satisfy

$${\mu }_{2n+i}/\delta =-q_i+O({\delta }^{-1}),i=1,2,\dots ,n,$$

that is,

$$\mid {\mu }_i+\delta q_{i-2n}\mid =\delta O({\delta }^{-1})=O(1),i=2n+1,2n+2,\dots ,3n.$$

Now for the 2n − 1 non-zero eigenvalues of Q with order O(δ^1/2), they are the solutions of

$$\mid \mathbf{Q}-{\mu }_i{\mathbf{I}}_{3n}\mid =0,i=2,\cdots ,2n.$$

For large δ, the matrix Q_CC − Q_CA − μ_iI_n is invertible, since it is strictly diagonal dominated. We can decompose the determinant as

$$\mid \mathbf{Q}-{\mu }_i{\mathbf{I}}_{3n}\mid =\mid \mathbf{U}({\mu }_i)\mid \mid {\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}-{\mu }_i{\mathbf{I}}_n\mid =0,$$

where

$$\mathbf{U}({\mu }_i)=\left[\begin{array}{cc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}-{\mu }_i{\mathbf{I}}_n& {\mathbf{Q}}_{AB}\\ {\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}{({\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}-{\mu }_i{\mathbf{I}}_n)}^{-1}{\mathbf{Q}}_{CA}& {\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}-{\mu }_i{\mathbf{I}}_n\end{array}\right].$$

Therefore, μ_i, i = 2, …, 2n, is also the eigenvalue of the matrix

$$\left[\begin{array}{cc}{\mathbf{Q}}_{AA}-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}\\ {\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}{({\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}-{\mu }_i{\mathbf{I}}_n)}^{-1}{\mathbf{Q}}_{CA}& {\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}\end{array}\right]=\mathbf{K}+\mathbf{S}$$

with

$$\mathbf{S}=\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ -{\mathbf{Q}}_{BC}-{\mathbf{Q}}_{BC}{({\mathbf{Q}}_{CC}-{\mathbf{Q}}_{CA}-{\mu }_i{\mathbf{I}}_n)}^{-1}{\mathbf{Q}}_{CA}& \mathbf{0}\end{array}\right].$$

We note that I_n +Q_BC(Q_CC − Q_CA − μ_iI_n)⁻¹Q_CA = (W − I_n)⁻¹ W, where $\mathbf{W}={\mathbf{Q}}_{CA}^{-1}({\mathbf{Q}}_{CC}-{\mu }_i{\mathbf{I}}_n)$. Since Q_CA is of the order O(δ) and μ_i is of the order O(δ^1/2), the entries of W are of the order O(δ^−1/2), so are the entries of S. Applying Lemma A.2 to K+ S tells us that for each μ_i there must be a eigenvalue κ_i of K, which has the property that

$${\mu }_i={\kappa }_i+O({\delta }^{-1/2}),i=2,\cdots ,2n.$$

PROOF of Theorem 4.1

We know from Lemma 3.1 that

$$\mathbf{M}={[{\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BC}-({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\mathbf{Q}}_{AA}]}^{-1}.$$

• Scenario 1. When Q_AA = 0, M = (Q_BB − Q_BC)⁻¹, so the eigenvalues and eigenvectors of −MQ_BC have nothing to do with [S].

• Scenario 2. When Q_BB = 0, ${(-\mathbf{M}{\mathbf{Q}}_{BC})}^{-1}={\mathbf{I}}_n-\frac{1}{[S]}{\mathbf{Q}}_{BC}^{-1}({\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC}){\stackrel{\sim }{\mathbf{Q}}}_{AB}^{-1}{\mathbf{Q}}_{AA}$. Thus, if −MQ_BC has eigenvalue λ_i(1) when [S] = 1, then for general [S], −MQ_BC has eigenvalue

  $${\lambda }_i[S]=\frac{1}{1-(1-{\lambda }_i^{-1}(1))/[S]}.$$
• Scenario 3. We write Q_AA = τQ̃_AA, where τ is large. Then −MQ_BC is

  $$\begin{array}{l}{(-{\mathbf{MQ}}_{BC})}^{-1}=\mathbf{I}-{\mathbf{Q}}_{BC}^{-1}{\mathbf{Q}}_{BB}+{\mathbf{Q}}_{BC}^{-1}({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\stackrel{\sim }{\mathbf{Q}}}_{AA}·\tau \\ =\tau [\frac{1}{\tau }(\mathbf{I}-{\mathbf{Q}}_{BC}^{-1}{\mathbf{Q}}_{BB})+{\mathbf{Q}}_{BC}^{-1}({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\stackrel{\sim }{\mathbf{Q}}}_{AA}].\end{array}$$
  Suppose the eigenvalues of ${\mathbf{Q}}_{BC}^{-1}({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\stackrel{\sim }{\mathbf{Q}}}_{AA}$ are 0, ${\lambda }_2^{\ast },\dots ,{\lambda }_n^{\ast }$. Then according to Lemma A.2, the eigenvalues of $\frac{1}{\tau }({\mathbf{I}}_n-{\mathbf{Q}}_{BC}^{-1}{\mathbf{Q}}_{BB})+({\mathbf{Q}}_{BB}-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}){\mathbf{Q}}_{AB}^{-1}{\stackrel{\sim }{\mathbf{Q}}}_{AA}$ are

  $$O({\tau }^{-1}),{\lambda }_2^{\ast }+O({\tau }^{-1}),\dots ,{\lambda }_n^{\ast }+O({\tau }^{-1}).$$
  Thus, the eigenvalues of −MQ_BC are

  $$1,\frac{1}{\tau {\lambda }_2^{\ast }+O(1)},\dots ,\frac{1}{\tau {\lambda }_n^{\ast }+O(1)},$$

  namely, all the none-one eigenvalues of −MQ_BC are of order τ⁻¹.

• Scenario 4. Using identical method as in Scenario 3, we can show that all the none-one eigenvalues of −MQ_BC are of order τ⁻¹.

PROOF of Theorem 4.2

The matrix K can be written as

$$\begin{array}{l}\mathbf{K}=\left(\begin{array}{cc}{\mathbf{I}}_{\alpha }-{\mathbf{Q}}_{AB}& {\mathbf{Q}}_{AB}\\ {\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC}& {\mathbf{I}}_{\beta }-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}\end{array}\right)+\left(\begin{array}{cc}{\mathbf{J}}_{\alpha }& \mathbf{0}\\ \mathbf{0}& {\mathbf{J}}_{\beta }\end{array}\right)\\ =\mathbf{T}+\left(\begin{array}{cc}{\mathbf{J}}_{\alpha }& \mathbf{0}\\ \mathbf{0}& {\mathbf{J}}_{\beta }\end{array}\right).\end{array}$$

We thus know from Lemma A.2 that the eigenvalues of K can be approximated by the eigenvalues of T. If |I_α − Q_AB − κI_n| is invertable, then

$$\mid \mathbf{T}-\kappa {\mathbf{I}}_n\mid =\mid {\mathbf{I}}_{\alpha }-{\mathbf{Q}}_{AB}-\kappa {\mathbf{I}}_n\mid ·\mid {\mathbf{I}}_{\beta }-{\mathbf{Q}}_{BA}-{\mathbf{Q}}_{BC}+({\mathbf{Q}}_{BA}+{\mathbf{Q}}_{BC}){(-{\mathbf{I}}_{\alpha }+{\mathbf{Q}}_{AB}+\kappa {\mathbf{I}}_n)}^{-1}{\mathbf{Q}}_{AB}-\kappa {\mathbf{I}}_n\mid ;$$

we know that any eigenvalue κ of T must make the second determinant on the right hand side zero. This determinant only involves diagonal matrices, so we have

$$\kappa -{\beta }_{ii}+k_{2i}+k_{-1i}=\frac{[S]k_{1i}(k_{2i}+k_{-1i})}{\kappa -{\alpha }_{ii}+[S]k_1}.$$ (A.2)

If |I_α − Q_AB − κI_n| is not invertible, then there is at least one j so that κ = α_jj − k_1j[S]. But it can be verified that in order to make κ an eigenvalue of T, there must exit another i ≠ j such that (A.2) holds for this κ. Therefore, any eigenvalue must be a root of (A.2).

(A.2) has two negative roots for each i, but we only need to consider the root closer to 0, since it dominates the decay.

• Scenario 1. α_ii = 0. The root is

  $${\kappa }_i=\frac{1}{2}\left(-([S]k_{1i}-{\beta }_{ii}+k_{-1i}+k_{2i})+\sqrt{{([S]k_1-{\beta }_{ii}+k_{-1i}+k_{2i})}^2+4{\beta }_{ii}[S]k_1}\right),$$

  which is monotone decreasing in [S].

• Scenario 2. β_ii = 0. The root is

  $${\kappa }_i=\frac{1}{2}\left(-([S]k_{1i}-{\alpha }_{ii}+k_{-1i}+k_{2i})+\sqrt{{([S]k_1-{\alpha }_{ii}+k_{-1i}+k_{2i})}^2+4{\alpha }_{ii}(k_{-1i}+k_{2i})}\right),$$

  which is monotone increasing in [S].

• Scenario 3. Q_AA = τQ̃_AA, where τ is large. Following the same method as we used in the proof of Theorem 3.9, we can show that n eigenvalues of K are of the order O(τ) and they will not contribute much to the correlation. The other eigenvalues governing the decay pattern can be approximated by the eigenvalues of Q_BB − Q_BA − Q_BC, which do not depend on the concentration [S].

• Scenario 4. Q_BB = τQ̃_BB, where τ is large. Using the same method as in the proof of Theorem 3.9, we can show that the dominating eigenvalues of K can be approximately by the eigenvalues of Q_AA − Q_AB. Since we know that Q_AA ≈ I_α, the eigenvalues of Q_AA − Q_AB is approximately α_ii − [S]k_1i, which is monotone decreasing in [S].