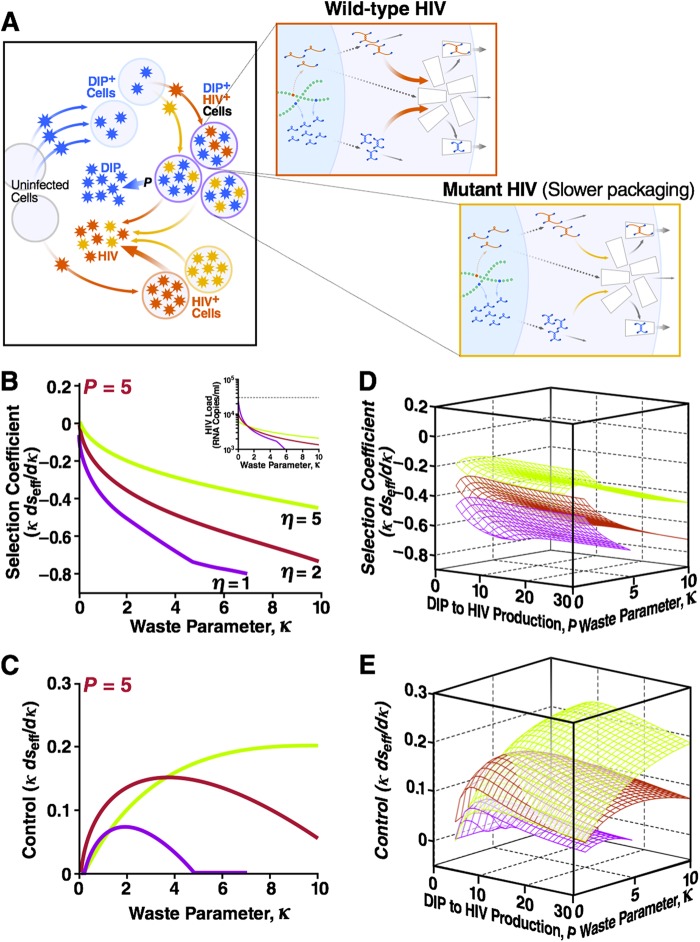
Fig 3.

A DIP-HIV interaction is evolutionarily stable over a broad parameter range: HIV-1 cannot escape DIP by decreasing packaging resources. (A) The two-scale model for an individual infected by two strains of HIV, wild type (red) and mutant (orange), as well as a DIP (blue). Mutation causes a small decrease in the packaging constant of both HIV-1 and DIP k_pck and, hence, an increase in capsid waste parameter, κ = αβ/(θk_pck), when ∂κ is >0. (B) Normalized effective selection coefficient, ∂s_eff/(∂κ/κ), for that mutation as a function of κ for a range of capsid-to-genome production ratios η. Fixed parameters are as described for Fig. 2B and C: R₀ = 10 and P = 5. The negative values of ∂s_eff/(∂κ/κ) imply that the mutation has net deleterious effects on HIV-1 replication. Overall, HIV-1 mutations that increase capsid waste are selected against. Inset, HIV-1 load as a function of the waste parameter from Fig. 2B. (C) A negative control showing ∂s_eff/(∂κ/κ) within HIV⁺ DIP⁺ dually infected cells when burst size changes due to increased capsid waste (the first term in equation S54 in the supplemental material) are neglected. Only in this specific context, when burst size changes are ignored, are HIV-1 mutations that increase capsid waste selected for. Shown also are the net ∂s_eff/(∂κ/κ) (D) and control ∂s_eff/(∂κ/κ) (i.e., when burst size changes are neglected) (E) as functions of both P and κ. These 3D plots act as a partial sensitivity analysis and show that the selection coefficient weakly depends on the value of P. Detailed calculations are given in Supplementary Methods in the supplemental material.