Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Jan 8;117(6):3055–3061. doi: 10.1021/jp309943k

Understanding Structure and Bonding of Multilayered Metal–Organic Nanostructures

David A Egger †, Victor G Ruiz ‡, Wissam A Saidi §, Tomáš Bučko ⊥,∥, Alexandre Tkatchenko ‡, Egbert Zojer †,*
PMCID: PMC3579432  PMID: 23447750

Abstract

graphic file with name jp-2012-09943k_0002.jpg

For organic and hybrid electronic devices, the physicochemical properties of the contained interfaces play a dominant role. To disentangle the various interactions occurring at such heterointerfaces, we here model a complex, yet prototypical, three-component system consisting of a Cu–phthalocyanine (CuPc) film on a 3,4,9,10-perylene-tetracarboxylic-dianhydride (PTCDA) monolayer adsorbed on Ag(111). The two encountered interfaces are similar, as in both cases there would be no bonding without van der Waals interactions. Still, they are also distinctly different, as only at the Ag(111)–PTCDA interface do massive charge-rearrangements occur. Using recently developed theoretical tools, we show that it has become possible to provide atomistic insight into the physical and chemical processes in this comparatively complex nanostructure distinguishing between interactions involving local rearrangements of the charge density and long-range van der Waals attraction.

1. Introduction

When different materials approach each other, the resulting physicochemical properties of the new heterostructures are often dictated by the interfaces. The latter become even more relevant, when the dimensions of the various materials are reduced and one encounters nanoscopic structures (in the present case molecular monolayers). As various types of such heterointerfaces have become integral parts of electronic devices, it is crucial to control their structure and properties for improving device performance. Beyond that it is appealing to design the interfaces’ physical and chemical properties to realize novel functionalities.1

Understanding the driving forces behind the formation of heterointerfaces and their consequences for the electronic properties2 of materials is challenging, as simultaneously occurring physical and chemical processes can blur a fully microscopic view on the relevant phenomena. Bonding often occurs due to a superposition of several sources of interaction such as charge-transfer, polarization, Pauli pushback, and van der Waals attraction; consequently, an unambiguous determination of the responsible binding mechanism becomes extremely difficult. This poses a considerable challenge when trying to understand the properties of more complex systems with several different interfaces.3,4 Here, atomistic modeling can aid in achieving an in-depth understanding of the relevant processes, as the latter can be traced back to the atomistic quantum-level and undesired external influences can often be excluded in a well-defined way. In passing we note that this also applies to situations where deviations from ideality such as the roughness of the interface determine the properties of a nanoscopic device, as discussed recently by Aradhya et al.5

In the present theoretical study, we focus on the problem of multiple interfaces in the area of organic electronics and study a prototypical multilayered heterostructure consisting of a Ag(111) metallic substrate onto which monolayers of the organic molecules 3,4,9,10-perylene-tetracarboxylic-dianhydride (PTCDA, see Figure 1a, top) and Cu-phthalocyanine (CuPc, see Figure 1a, bottom) are successively adsorbed (Ag(111)–PTCDA–CuPc, Figure 1, parts b and c). The motivation for the choice of this system is 3-fold: (i) It contains two qualitatively different interfaces (one between a metal and an organic semiconductor and one between two organic layers), where different mechanisms can be expected to establish bonding. (ii) The two interfaces are very close (separated only by a PTCDA monolayer) and, thus, can be expected to influence each other.3 (iii) The Ag(111)–PTCDA–CuPc system is, to the best of our knowledge, the only metal–organic–organic three-layer system for which full experimental information on its geometric structure has been published.3

Figure 1.

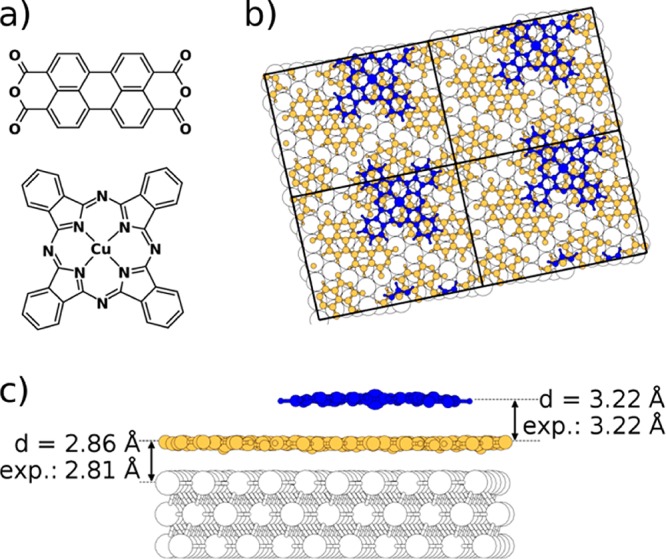
Figure 1

Open in a new tab

(a) Chemical structures of the studied organic molecules: 3,4,9,10-perylene-tetracarboxylic-dianhydride (PTCDA; top) and Cu–phthalocyanine (CuPc; bottom). Top (b) and side view (c) of CuPc (blue) on PTCDA (yellow) on Ag(111) (white); the considered unit cell is indicated in part b; the calculated and experimental3 average distances are listed in part c. The former were extracted from a full geometry optimization, see main text.

Analyzing the energetic contributions to Ag(111)–PTCDA–CuPc bonding and the resulting charge-transfer at the atomistic quantum-level, we find that for both, the Ag(111)–PTCDA and the PTCDA–CuPc interfaces, no appreciable bonding would occur in the absence of long-range van der Waals (vdW) interactions. The charge-rearrangements are, however, by nearly 2 orders of magnitude larger for the formation of the interface between Ag(111) and PTCDA than for the addition of the CuPc layer, where in the former case the main effect is electron transfer from the metal substrate to the PTCDA monolayer. This hints toward relatively involved binding mechanisms for the Ag(111)–PTCDA–CuPc structure.

2. Theoretical Methods and System Setup

Modeling complex hybrid metal–organic systems is a sizable challenge and due to system size, atomistic modeling usually relies on density-functional theory (DFT), where long-range vdW contributions to the total energy are missing in common (semi)local approximations.6 Employing these (semi)local density functionals can, therefore, result in an erroneous description of the binding process and a wrong prediction of the interfacial structure of hybrid metal–organic systems.6

Here, we show that this problem can be overcome and a reliable description of the key structural properties of the above-described multilayered heterostructure has now become possible. To this end, we employ the Perdew–Burke–Enzerhof (PBE) exchange-correlation functional7 and include long-range vdW interactions through the recently developed PBE + vdWsurf scheme.8 The latter seamlessly combines the Lifshitz–Zaremba–Kohn (LZK) theory9,10 of the vdW interaction between an atom and a solid surface with the dispersion-inclusive PBE + vdW11 method. Hence, the PBE + vdWsurf method simultaneously captures the local hybridization effects within the molecule, surface polarization effects, and the many-body response screening within the metallic bulk. It has so far been successfully applied to binary systems such as Xe, benzene, and PTCDA on transition metals8 and to 2-pyrrolidone on Ag(111) and Ag(100) surfaces.12 To describe laterally extended interfaces, slab-type band-structure calculations (plane-wave cutoff: ∼270 eV) were employed using a modified version of the VASP code,13 where PBE + vdWsurf has been implemented.14 Core–valence interactions were treated in the projected augmented wave formalism15 using soft potentials.16 3D representations of the calculated systems were generated with XCrysden.17

To model Ag(111)–PTCDA–CuPc, we started from the surface unit-cell observed in STM for PTCDA on Ag(111),18 whereby the lattice parameter a was set to the value of 4.03 Å that corresponds to the lattice constant of Ag optimized using the PBE + vdWsurf method. This unit cell has been found to prevail within the PTCDA layer also in the Ag(111)–PTCDA–CuPc system.3 We doubled the unit cell in one direction (see Figure 1b), which allowed us to define a structural model with one CuPc molecule per simulation cell. This results in the final unit cell containing one CuPc and four PTCDA molecules, three layers of Ag(111) and altogether more than 400 atoms (Figure 1b and Figure 1c). We note that the experimentally observed unit cell of commensurate Ag(111)–PTCDA–CuPc at full CuPc coverage is even larger by a factor of 2.5 and also contains a larger fraction of CuPc molecules (four CuPc and ten PTCDA molecules per unit cell).3 Our structural model, however, provides a CuPc coverage close to the packing for which the vertical bonding distances have been reported in ref (3).19 Further details on the computational methodology and system setup are described in the Supporting Information.

3. Results and Discussion

3.1. Bonding in the Ag(111)–PTCDA–CuPc Heterostructure

We first analyze the interactions between a CuPc layer and Ag(111)–PTCDA by calculating its binding-energy curve as a function of the vertical distance, d, separating the CuPc layer from Ag(111)–PTCDA. The binding energy EB(d) is then obtained as

3.1. 1

where Esys is the energy of the complete heterostructure Ag(111)–PTCDA–CuPc, Esub is the energy of the “substrate” (here, the PTCDA layer on silver) and Eads the energy of the adsorbate (here, the CuPc layer, for further details see the Supporting Information). By calculating EB(d) separately with PBE + vdWsurf and pure PBE, i.e., effectively including and neglecting vdW interactions, we are capable of assessing their role in the bonding of CuPc to Ag(111)–PTCDA. The results in Figure 2 show that no bonding between CuPc and Ag(111)–PTCDA is predicted in the absence of long-range vdW interactions, revealing their importance in establishing the Ag(111)–PTCDA–CuPc interface. Notably, vdW interactions, which are commonly thought of as being “weak”, are in the range of several eV and thus substantially contribute to the relatively large binding energy between Ag(111)–PTCDA and CuPc of ∼2.7 eV per CuPc molecule. This is primarily a consequence of the size of the interacting molecules, as the vdW contribution to the overall binding energy of 2.7 eV amount to a quite moderate ∼0.1 eV per heavy atom in CuPc. Compared to experiment3 (dashed vertical line in Figure 2), the equilibrium distance calculated with PBE + vdWsurf is already encouraging given that here only a single geometric parameter (the bonding distance) has been “optimized”.

Figure 2.

Figure 2

Open in a new tab

Binding energy EB between the CuPc layer and Ag(111)–PTCDA as a function of the difference between the average vertical positions of the carbon atoms in the PTCDA and CuPc layers calculated with PBE (red) and PBE + vdWsurf (green); the dashed vertical line indicates the experimental distance.3

For the metal–organic interface between Ag(111) and PTCDA, it is well-known that an equilibrating electron transfer from the silver surface into the band derived from the lowest unoccupied molecular orbital of the PTCDA molecules (former LUMO; F-LUMO) pins that band to the Fermi level.3,20 Nevertheless, it was repeatedly seen when modeling the Ag(111)–PTCDA structure that only the proper inclusion of vdW interactions yields a realistic binding-energy profile,6,8,21,22 indicating that a combination of several different binding interactions is responsible for the formation of the Ag(111)–PTCDA interface.

This raises the question, to what extent those interactions are modified by the presence of a CuPc layer (cf., discussion in ref (3)). To elucidate this, we compare the binding-energy curves for the PTCDA–CuPc double-layer and the PTCDA single-layer on Ag(111) in Figure 3a (again obtained from calculating the energy difference of the respective combined and separated systems, see Supporting Information for details). As can be seen from the figure, the two binding energy curves are similar, but the PTCDA–CuPc double-layer binds slightly more strongly to Ag(111) than the PTCDA single-layer alone. The origin of this difference can be traced back to the PBE and vdWsurf parts of the respective binding-energy curves (see Supporting Information). Calculating the corresponding binding-energy differences (see Figure 3b) allows disentangling the pure long-range vdW contribution (vdWsurf) from all other chemical/physical interactions (PBE). The data show that primarily the vdW attraction between PTCDA–CuPc and the silver surface is stronger compared to the PTCDA single-layer on Ag(111). With an energy contribution of ∼0.12 eV at the equilibrium distance, this effect is relatively small compared to the total vdW attractive energy between Ag(111) and PTCDA–CuPc, which amounts to ca. 2.9 eV at the same distance (see Supporting Information). Nevertheless, the other energetic contributions to ΔEB are clearly less affected by the presence of the CuPc layer. The two main effects contributing to this additional van der Waals interaction can be traced back to (i) the direct vdW attraction between CuPc and the Ag(111) substrate (calculated by removing the PTCDA layer and amounting to 0.07 eV at the equilibrium distance) and (ii) an increased PTCDA–CuPc vdW interaction due to the charge transfer between the Ag(111) substrate and the PTCDA layer. The latter occurs because the charge transfer increases the PTCDA’s molecular C6 coefficients by 11% compared to those of the monolayer in the absence of Ag (111) (cf., ref (8)). That this effect is accounted for in our calculations is an intrinsic advantage of the applied PBE + vdWsurf scheme, where the determination of the C6 parameters involves a Hirshfeld partitioning of the charge density and, thus, is affected by charge-transfer effects.11

Figure 3.

Figure 3

Open in a new tab

(a) PBE + vdWsurf binding-energy curves of a PTCDA single-layer (black) and a PTCDA–CuPc double-layer (gray), adsorbing on Ag(111) as a function of the Ag(111)–PTCDA distance; dashed vertical lines indicate the experimental binding distances for PTCDA20 (black) and PTCDA–CuPc3 (gray) on Ag(111). (b) Binding-energy difference ΔEB of the two curves in part a with the respective PBE (red) and vdWsurf (cyan) energy contributions.

The detailed interfacial atomic structure critically affects the electronic properties of interfaces such as the work function, the alignment between electronic levels, and the adsorption-induced charge transfer.22 To obtain the latter and also to fully benchmark our calculations against experiments in which, naturally, all nuclear degrees of freedom (and not only the interlayer distance) are relaxed, we performed a full geometry relaxation of the Ag(111)–PTCDA–CuPc system (using the GADGET tool;23 for further details see Supporting Information). This improves the description of equilibrium adsorption distances compared to the approximate value obtained in binding-energy curves (Figure 2 and 3a). The finally obtained adsorption distances (determined by the average carbon positions in the PTCDA and CuPc layers and the hypothetical position of the unrelaxed top Ag layer) are compared to the corresponding experimental result in Figure 1c: Both the metal–organic as well as the organic–organic interlayer distances compare exceptionally well to experimental values.3 Moreover, we find that the adsorption of CuPc on top of Ag(111)–PTCDA pushes the PTCDA layer toward the silver surface by on average 0.05 Å (2.86 Å vs 2.91 Å), a subtle geometric effect also seen for the average distances in the experiment (2.81 Å vs 2.86 Å).3 Interestingly, when examining the four inequivalent PTCDA molecules in the unit cell, the calculations reveal variations in the individual adsorption distances between 2.83 and 2.88 Å, depending on how much a PTCDA molecule is “covered” by the CuPc. This effect is not captured by the binding-energy curves, where all layers are assumed to be flat; it is, thus, a possible reason why there the minimum positions are shifted only very slightly (by only 0.01 Å) upon CuPc adsorption (cf., Figure 3a).

3.2. Charge Rearrangements at the Ag(111)–PTCDA and PTCDA–CuPc Interfaces

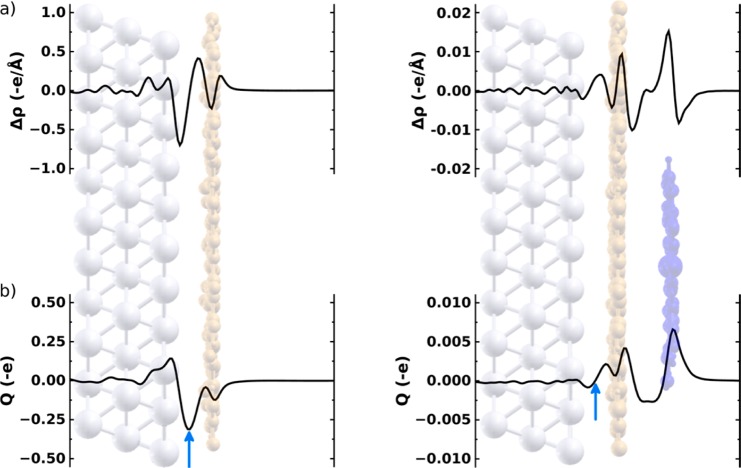
With a reliable adsorption geometry at hand, assessing the adsorption-induced charge rearrangements, Δρ, between the various layers becomes possible. This quantity is interesting as it sheds light onto bonding between CuPc and Ag(111)–PTCDA beyond vdW interactions and provides insight into the extent to which the Ag(111)–PTCDA interaction is modified by CuPc adsorption. Moreover, it directly translates into a work-function change ΔΦ via the Poisson equation. The profound charge rearrangements due to Ag(111)–PTCDA interface formation are shown integrated over the xy-plane per PTCDA molecule in Figure 4a (left) and as isodensity plots in Figure 5, parts a and b. They hint toward an interaction between PTCDA and Ag(111) far beyond vdW, as discussed in detail in refs (20, 22, 24), and (25). The electron density right above the Ag(111) surface is reduced with the primary reduction occurring below the carboxylic oxygens of the PTCDA layer (see Figure 5a),25 and some of the charge is redistributed to the region around the top metal layer (as one would expect for Pauli push-back). The main effect, however, is a transfer of electron density to the π-system of PTCDA associated with a filling of the F-LUMO (see Figure 5a)20,22 that results in Fermi-level pinning. This is accompanied by a somewhat reduced charge density in the σ-orbitals (i.e., in the plane of the molecule) with the largest effect around the carboxylic oxygens. The latter is often observed for the adsorption of acceptor layers and can be related to back-donation processes.26 To obtain an alternative view of the adsorption-induced charge transfer, we integrate Δρ over distance to obtain the cumulative charge rearrangements Q:27 A negative value of Q (when plotted in units of −e, with e representing the positive elementary charge) at a given position specifies the number of electrons transferred from left-to-right of a plane at that position; correspondingly, a positive value of Q denotes a transfer from right to left and a Q value of zero means that on average no charge is shifted across this plane. For PTCDA adsorbing on Ag(111), Q is indeed substantial (Figure 4b, left) and the (negative) maximum between Ag(111) and PTCDA (indicated by a blue arrow) shows that the net transfer amounts to ca. 0.31 electrons per PTCDA molecule (for more details, see ref (22).).

Figure 4.

Figure 4

Open in a new tab

Plane-integrated charge rearrangements Δρ (a) and cumulative charge transfer Q (b) induced upon PTCDA adsorption onto Ag(111) (left) and CuPc adsorption onto Ag(111)–PTCDA (right). These quanitites are calculated from the charge-density differences of the combined systems (left, Ag(111)–PTCDA; right, Ag(111)–PTCDA–CuPc) and the respective subsystems (left, Ag(111) and PTCDA; right, Ag(111)–PTCDA and CuPc). Δρ and Q are reported per PTCDA molecule. Note that the scales in the left and right part differ by a factor of 50. “e” refers to the (positive) elementary charge; consequently, negative values in the Δρ-plot correspond to a reduction of the electron density, while positive Δρ are a manifestation of electron accumulation. For the meaning of the sign of Q, see main text.

Figure 5.

Figure 5

Open in a new tab

Isodensity plots depicting charge rearrangements upon adsorption of a PTCDA single-layer onto a Ag(111) surface (a, b) and a CuPc layer onto Ag(111)–PTCDA (c, d). Blue (red) regions denote electron accumulation (depletion). Note that due to the much smaller charge rearrangements upon CuPc adsorption, the isodensity value used for parts c and d has been reduced by a factor of 28.

The adsorption of the CuPc layer impacts the interfacial charge rearrangements only to a very small extent. Overall two effects need to be considered: (i) The PTCDA layer is pushed closer to the substrate, which slightly reduces the distortion of the carboxylic oxygens and, thus, the intrinsic dipole moment of the PTCDA layer. As expected when being in the Fermi-level pinning regime,28 this decreases the charge-transfer induced dipole between Ag and PTCDA that counteracts the intrinsic molecular dipole. The effect is, however, small (amounting to a reduction of the absolute value of the maximum of Q by 0.02 e) and considering that we do not observe an associated destabilization of the F-LUMO peak, it is attributed to an increase of the above-mentioned back-donation from σ-orbitals. Moreover, the absolute numbers have to be treated with some caution as they are directly related to the positions of the carboxylic oxygens relative to the backbone, which are only quite poorly described when using soft PAW potentials.16 Our tests described in the Supporting Information however indicate that their impact on the comparison of the situations with and without CuPc layer is only minor.

(ii) The main observation for the additional Δρ when also adding the CuPc layer (Figure 4a, right) is that the magnitude of the calculated peaks is by a factor of ∼50 smaller than the Δρ observed for the interaction between PTCDA and Ag(111). Moreover, the additional Δρ is essentially confined to the organic layers; i.e., there is no further impact on the charge-transfer between Ag(111) and PTCDA as can also be inferred from the corresponding Q in the right part of Figure 4b crossing the zero line between the Ag substrate and the PTCDA layer (indicated by the blue arrow). We find also no clear indications for Pauli push-back between the organic layers (even at the strongly inflated Δρ scale used in Figure 4a). This is ascribed to a — relative to the metal substrate — massively reduced polarizability of the electron cloud in the organic layers and to a stronger spatial confinement of the electrons (i.e., a reduced tailing of the charge density above the PTCDA layer, as plotted in the Supporting Information). The 3D charge-rearrangement pattern for CuPc adsorption shown in Figure 5, parts c and d, is relatively complex and does not allow a clear identification of specific “modes” of interaction. An interesting observation is the electron depletion above the PTCDA layer especially underneath the CuPc molecules. This is accompanied by charge accumulations directly above the PTCDA layer, especially further away from the CuPc molecules, and also in the region directly below the CuPc layer.

The negative values of Q between the PTCDA and CuPc layers indicate a very minor (0.003 electrons per CuPc molecule) electron transfer from PTCDA to CuPc consistent with the isodensity plot in Figure 5, parts c and d. Moreover, both organic layers appear somewhat polarized (cf., Figure 4, right plots) such that electron density is shifted from above the planes of the molecular backbones to below. Regarding this analysis it, however, needs to be kept in mind that the overall magnitude of all rearrangements observed at the PTCDA/CuPc interface are very minor probably reaching the accuracy limit of state of the art calculations.

3.3. Work-Function Changes and the Density of States

The above-described interfacial charge rearrangements together with the possible dipole moment of an adsorbing layer determine the adsorption-induced work-function modification ΔΦ. For PTCDA adsorption on Ag(111), electron transfer from the metal to the organic adsorbate dominates over the push-back, which together would result in an increase of the work function by ΔΦΔρ = 0.41 eV. This effect is, however, diminished by the intrinsic dipole of the PTCDA layer (vide infra). The latter originates from the C and O atoms not being in the same plane.20,22 Regarding the impact of additionally adsorbing the CuPc molecules, a first observation is the only very small intrinsic dipole moment associated with the adsorbed CuPc monolayer amounting to an additional work-function increase on the order of 0.01 eV. Thus, adsorbing CuPc on Ag(111)–PTCDA could induce a significant ΔΦ only via charge rearrangements. As discussed in the preceding section, the latter are, however, extremely small. Therefore, it is not surprising that in all cases we studied, ΔΦ relative to the bare Ag(111) surface is calculated to lie between 0.04 and 0.05 eV for both the fully optimized Ag(111)–PTCDA and Ag(111)–PTCDA–CuPc system.29 For Ag(111)–PTCDA, this value is in good agreement with ΔΦ = 0.1 eV measured for PTCDA on Ag(111) by Zou et al.30 A comparative experimental investigation of ΔΦ for Ag(111)–PTCDA–CuPc and Ag(111)–PTCDA interfaces, thus, would provide a straightforward way to test the above predictions regarding interfacial charge transfer; to the best of our knowledge, such data on Ag(111)–PTCDA–CuPc are, however, not yet available.

Alternatively, one can compare the valence photoelectron spectra for the two systems as done in ref (3). In the calculations (cf., Supporting Information), we obtain a good qualitative agreement between theoretical and experimental spectra confirming also the assignment in ref (3) of the various peaks to ionization processes within either the PTCDA or CuPc layers; in particular, the association of the highest binding energy feature to the partially filled F-LUMO of PTCDA is supported by the calculations. Associating the measured small (at the maximum 0.12 eV) shift of the PTCDA F-LUMO feature in the valence photoelectron spectrum upon CuPc deposition with charge rearrangements between the Ag(111) substrate and the PTCDA layer (as suggested in ref (3)) is, however, potentially complicated by the observation in tunneling spectroscopy experiments that the peak due to the F-LUMO consists of two maxima split by 0.16 eV.24,25 These arise from the inequivalent molecules in the PTCDA unit cell. As a consequence, an apparent shift of the F-LUMO feature could also be a consequence of cross-section redistributions between the two peaks due to the inequivalent molecules, caused, e.g., by the minor charge rearrangements between PTCDA and CuPc discussed in the previous section or by “shielding” of photoelectrons from the PTCDA layer by CuPc molecules. This effect, however, cannot be captured by our simulations as (i) the calculation of valence photoelectron cross sections would go far beyond the scope of the present paper and (ii) the splitting between the two inequivalent molecules on the Ag(111) surface is not properly recovered by our DFT calculations in analogy to what is described in ref (25). The latter could, indeed, be the explanation, why in the calculations the F-LUMO peak shifts by only 0.01 eV due to the CuPc (note that this value has been obtained at a reduced CuPc coverage as described in section 2). The experimental observation that the position of the former PTCDA HOMO virtually does not shift with increasing CuPc coverage,3 in fact supports the notion that the electronic states in the PTCDA layer are not rigidly shifted relative to the metal states by some interfacial charge rearrangements induced by CuPc adsorption. (Note that for the former PTCDA HOMO, differences between the two inequivalent molecules in the unit cell are expected to be of only minor relevance, as for the associated feature the above-described tunneling spectroscopy measurements revealed a splitting of only 0.04 eV.24,25) These considerations show that a full explanation of all details of the measured valence photoelectron spectra including the presence or absence of small peak shifts by the present calculations remains, however, elusive due to the sheer system size that imposes limitations both on the chosen model unit-cell as well as on the applied computational tools (requiring, e.g., the use of relatively few metal layers to describe the substrate and the application of soft PAW-potentials combined with a relatively sparse k-point grid). Further details on the discussion in this paragraph can be found in the Supporting Information together with the calculated density of states.

4. Conclusions

In summary, we have studied the bonding in a complex three-component system that contains different heterointerfaces. It serves as a prototypical example for portraying the intricate interplay of different processes that determine the interfacial structure in organic nanostructures and also for highlighting the potential of modern computational modeling tools: In Ag(111)–PTCDA–CuPc, the bonding-induced charge transfer is vastly different at the metal–organic (Ag(111)–PTCDA) and the organic–organic (PTCDA–CuPc) interface with very small charge redistributions in the latter case. These coincide with an only very minor additional modification of the system work-function by the adsorbing CuPc layer. While certain ambiguities regarding the interpretation of the calculated density of states and the valence photoelectron spectra in ref (3) remain, it is clearly shown here that bonding for both interfaces is vastly dominated by long-range vdW interactions. Their magnitude is large for both interfaces (ca. 3 eV at the equilibrium distances) rendering a characterization of such interfaces as weakly bonded questionable, even if the dominant interaction strength does not originate from a single, strong bond but from the combined attraction of all atoms that are part of the interacting subsystems. To put the magnitude of the vdW interactions into perspective, it is interesting to remember that the significant charge rearrangements at the Ag(111)/PTCDA interface alone do not result in any appreciable bonding interaction. In passing, we note that such strong binding due to vdW interactions has recently also been extracted from scanning tunneling and atomic force microscope measurements of PTCDA on Au(111).31

These results show that a fully quantitative description of metal–organic interfaces without considering vdW interactions is not generally possible and restricted to very few systems that bond, e.g., through suitable anchoring groups. Our data, however, also indicate that by including vdW interactions at surfaces using the recently developed PBE + vdWsurf scheme, the necessary reliable description of the geometric structure has become an achievable goal even for large and complex hybrid metal–organic systems. We conclude that with suitable theoretical tools becoming increasingly available, computational modeling can indeed contribute to deriving a detailed microscopic picture of complex hybrid nanostructures.

Acknowledgments

The authors thank B. Stadtmüller and C. Kumpf for helpful discussions. D.A.E. is a recipient of a DOC fellowship by the Austrian Academy of Sciences. Financial support by the Austrian Science Fund (FWF), P24666-N20, and from the FP7 Marie Curie Actions of the European Commission, via the Initial Training Network SMALL (MCITN-238804) is gratefully acknowledged. A.T. is supported by a grant from the European Research Council (ERC Starting Grant VDW-CMAT). T.B. receives support by the VASP project and by the Slovak Research and Development Agency under the contract No. APVV-0059-10. Our calculations have been performed at the icluster (ZID TU Graz) and the VSC-2 (Vienna Scientific Cluster).

Supporting Information Available

Details on the methodology and system setup, various tests assessing the reliability of our simulations, additional binding-energy curves, calculations of the tailing of the electron clouds, and discussion of the calculated density of states. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

jp309943k_si_001.pdf (442.7KB, pdf)

References

  1. Koch N. ChemPhysChem 2007, 8, 1438–1455. [DOI] [PubMed] [Google Scholar]
  2. Ishii H.; Sugiyama K.; Ito E.; Seki K. Adv. Mater. 1999, 11, 605–625. [Google Scholar]
  3. Stadtmüller B.; Sueyoshi T.; Kichin G.; Kröger I.; Soubatch S.; Temirov R.; Tautz F.; Kumpf C. Phys. Rev. Lett. 2012, 108, 106103. [DOI] [PubMed] [Google Scholar]
  4. Niederhausen J.; Amsalem P.; Wilke A.; Schlesinger R.; Winkler S.; Vollmer A.; Rabe J.; Koch N. Phys. Rev. B 2012, 86, 081411(R). [Google Scholar]
  5. Aradhya S. V.; Frei M.; Hybertsen M. S.; Venkataraman L. Nat. Mater. 2012, 11, 872–876. [DOI] [PubMed] [Google Scholar]
  6. Tkatchenko A.; Romaner L.; Hofmann O. T.; Zojer E.; Ambrosch-Draxl C.; Scheffler M. MRS Bull. 2011, 35, 435–442. [Google Scholar]
  7. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
  8. Ruiz V.; Liu W.; Zojer E.; Scheffler M.; Tkatchenko A. Phys. Rev. Lett. 2012, 108, 146103. [DOI] [PubMed] [Google Scholar]
  9. Lifshits E. M. Sov. Phys. JETP 1956, 2, 73. [Google Scholar]
  10. Zaremba E.; Kohn W. Phys. Rev. B 1976, 13, 2270–2285. [Google Scholar]
  11. Tkatchenko A.; Scheffler M. Phys. Rev. Lett. 2009, 102, 073005. [DOI] [PubMed] [Google Scholar]
  12. Al-Saidi W. A.; Feng H.; Fichthorn K. A. Nano Lett. 2012, 12, 997–1001. [DOI] [PubMed] [Google Scholar]
  13. Kresse G.; Furthmüller J. Phys. Rev. B 1996, 54, 11169–11186. [DOI] [PubMed] [Google Scholar]
  14. Al-Saidi W. A.; Voora V. K.; Jordan K. D. J. Chem. Theory Comput. 2012, 8, 1503–1513. [DOI] [PubMed] [Google Scholar]
  15. Kresse G.; Joubert D. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
  16. For a description of test-calculations using harder potentials, see the Supporting Information.
  17. Kokalj A. Comput. Mater. Sci. 2003, 28, 155. [Google Scholar]
  18. Glöckler K.; Seidel C.; Soukopp A.; Sokolowski M.; Umbach E.; Böhringer M.; Berndt R.; Schneider W.-D. Surf. Sci. 1998, 405, 1–20. [Google Scholar]
  19. It corresponds to 60% of the experimentally observed full coverage, which is only by a factor of ca. 1.5 larger than the coverage chosen in the calculations.; Stadtmüller B. ; Kumpf C. Private communication.
  20. Hauschild A.; Karki K.; Cowie B.; Rohlfing M.; Tautz F.; Sokolowski M. Phys. Rev. Lett. 2005, 94, 036106. [DOI] [PubMed] [Google Scholar]
  21. Rohlfing M.; Bredow T. Phys. Rev. Lett. 2008, 101, 266106. [DOI] [PubMed] [Google Scholar]
  22. Romaner L.; Nabok D.; Puschnig P.; Zojer E.; Ambrosch-Draxl C. New J. Phys. 2009, 11, 053010. [Google Scholar]
  23. Bučko T.; Hafner J.; Ángyán J. G. J. Chem. Phys. 2005, 122, 124508. [DOI] [PubMed] [Google Scholar]
  24. Kraft A.; Temirov R.; Henze S. K. M.; Soubatch S.; Rohlfing M.; Tautz F. S. Phys. Rev. B 2006, 74, 041402(R). [Google Scholar]
  25. Rohlfing M.; Temirov R.; Tautz F. Phys. Rev. B 2007, 76, 115421. [Google Scholar]
  26. Romaner L.; Heimel G.; Brédas J. L.; Gerlach A.; Schreiber F.; Johnson R. L.; Zegenhagen J.; Duhm S.; Koch N.; Zojer E. Phys. Rev. Lett. 2007, 99, 256801. [DOI] [PubMed] [Google Scholar]
  27. Stadler R.; Jacobsen K. W. Phys. Rev. B 2006, 74, 161405 (R). [Google Scholar]
  28. Hofmann O. T.; Egger D. A.; Zojer E. Nano Lett. 2010, 10, 4369. [DOI] [PubMed] [Google Scholar]
  29. A closer inspection reveals that the impact of the CuPc layer arises not only from its very minor intrinsic dipole, but is also impacted by the small charge rearrangements shown in Figure 4 and by the consequences arising from the modified adsorption distance of the PTCDA layer. All three effects are of comparable magnitude and amount to ∼0.01 eV with the intrinsic dipole and reduced adsorption distance giving rise to a work-function increase that is partially compensated by the charge rearrangements at the PTCDA/CuPc interface. A further analysis of these tiny effects does not appear particularly useful.
  30. Zou Y.; Kilian L.; Schöll A.; Schmidt T.; Fink R.; Umbach E. Surf. Sci. 2006, 600, 1240–1251. [Google Scholar]
  31. Wagner C.; Fournier N.; Tautz F.; Temirov R. Phys. Rev. Lett. 2012, 109, 076102. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp309943k_si_001.pdf (442.7KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES