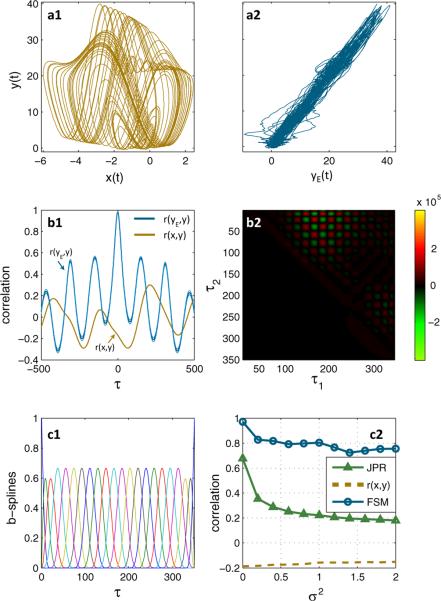
FIG. 1.

(Color online) Identification of nonlinear interaction in a coupled Rössler-Lorenz system. a1): Nonlinear synchronization manifold between original sampled data x and y (the systems' 3^rd coordinates) in generalized synchronization with correlation r(x, y) = −0.168. a2: Linearized manifold between yE and y, where yE(t) = F[x](t) is the output of a 2^nd order Volterra model, yielding r(yE, y) = 0.98. b1) Delay-shifted (by τ) correlation coeffcients. b2) 2^nd order kernel corresponding to a2). c1) Set of cubic b-splines corresponding to b2), used in eq. (3). c2) Performance of the method (FSM, r(yE, y) ∈ [−1, 1]) for Rössler-Lorenz system with additive white noise over increasing variance σ², compared against correlation r(x, y), as well as the JPR ∈ [0, 1].