Robust Multiscale Stereo Matching from Fundus Images with Radiometric Differences

Abstract

A robust multiscale stereo matching algorithm is proposed to find reliable correspondences between low contrast and weakly textured retinal image pairs with radiometric differences. Existing algorithms designed to deal with piecewise planar surfaces with distinct features and Lambertian reflectance do not apply in applications such as 3D reconstruction of medical images including stereo retinal images. In this paper, robust pixel feature vectors are formulated to extract discriminative features in the presence of noise in scale space, through which the response of low-frequency mechanisms alter and interact with the response of high-frequency mechanisms. The deep structures of the scene are represented with the evolution of disparity estimates in scale space, which distributes the matching ambiguity along the scale dimension to obtain globally coherent reconstructions. The performance is verified both qualitatively by face validity and quantitatively on our collection of stereo fundus image sets with ground truth, which have been made publicly available as an extension of standard test images for performance evaluation.

1 Introduction

Depth from stereo has been a challenging problem in computer vision for decades [2], [14], [33]. It involves the estimation of 3D shape or depth differences using two images of the same scene under slightly different geometry. By measuring the relative position differences or disparity of one or more corresponding patches or regions in the two images, shape can be estimated [31]. The identification of these corresponding patches is called the “correspondence problem” [33]. Commonly, the disparity d of a point-pair s₁ and s₂ associated with the same 3D point S in a pair of regions of given similarity is expressed as their coordinate difference on the planes projected by imaging systems P₁ and P₂. Similarity of the two images increases the ease of this estimation. Shape or depth differences are thus distinguished by disparities of corresponding points, patches, or regions:

$$d=s_2-s_1,\text{ where }{s}_1=P_1(S),s_2=P_2(S).$$ (1)

However, the assumption that a 3D point in space has the same appearance under projection from different geometries is not always true, even if imaging conditions remain ideal. Some of these reasons include:

• A change of viewing angle will cause a shift in perceived (specular) reflection and hue of the surface if the illumination source is not at infinity or the surface does not exhibit Lambertian reflectance [28].

• Focus and defocus may occur in different planes at different viewing angles if depth of field (DOF) is not unlimited [32].

• A change of viewing angle may cause geometric image distortion or the effect of perspective foreshortening [24] if the imaging plane is not at infinity. Large depth variations of one point relative to its surrounding points may violate the ordering constraint [10] or produce occlusions.

• A change of viewing angle or temporal change may also change geometry and reflectance of the surfaces if the images are not obtained simultaneously, but, instead, sequentially [1].

Even small errors of the disparity estimate may result in large depth deviations from the truth, making robust and accurate stereo matching from noisy image data a challenging problem.

The Middlebury stereo vision benchmark (http://vision.middlebury.edu/stereo/) and related publications [8], [9], [21], [22], [26] have greatly advanced the state of art in stereo correspondence algorithms. Idiosyncrasies in the offered data sets, coupled with the competitive format, have resulted in ever better performing algorithms on these publicly available data sets, and researchers have attempted to increase performance by making using of these idiosyncrasies. Many of the most successful global optimization methods [8], [9], [22] are based on segmentation into regions, and thus are only valid if the stereo pair contains piecewise planar surfaces, with intensity boundaries of each segmented region being in agreement with depth discontinuities [22].

When we applied the “top ranked Middlebury algorithms” to derive depth in retinal stereo images, their performance was unacceptably low. In such images, the Lambertian reflectance model does not apply, the surface (of the retina) has low contrast, low density texture, there is substantial noise because of limitations on the amount of illumination (for patient safety, coupled with limited quantum efficiency of the image sensors), and there is vertical disparity. The idiosyncrasies in the Middlebury data sets are in fact not present in such applications, and thus the constraints in the top-performing algorithms are invalid. Therefore, a better approach is required to accurately estimate depth from stereo in these as well as retinal stereo images.

The Middlebury data sets come with a reference standard for depth which is radiometrically clean [38]. For stereo images that do not conform to the Middlebury assumptions, such reference standards are not available. We have therefore developed a reference standard for retinal stereo color images [19] which can serve as a quantitative testbed for performance evaluation of different algorithms on images originating from practical applications that do not conform with these assumptions. Medically, detecting the shape of the optic nerve head (ONH) in stereo images of the retina is of great interest because it allows better management of patients with glaucoma, a leading preventable cause of blindness in the world.

The contributions of this paper are twofold. First, we present a coarse-to-fine stereo matching method for retinal stereo images, which typically do not satisfy brightness constancy assumption and have weakly textured and out-of-focus regions. The ordering constraint is supposed to be kept in this scenario. Descriptors dealing with occlusions and violations of the ordering constraint can be found in [44] and [46] for wide baseline stereo. Second, we propose to extend the current collection of standard test images with our stereo fundus image sets by making them publicly available in de-identified form with ground truth for quantitative performance validation (http://webeye.ophth.uiowa.edu/component/k2/item/270).

The paper is organized as follows: In Section 2, we overview existing stereo matching approaches and their problems in practical applications. In Section 3, we address key issues in robust disparity estimate and give our solution. Experimental results are presented in Section 4, and Section 5 concludes the paper with some discussions.

2 Problem Overview

2.1 Depth from Stereo: General Approach

Depth from stereo is usually performed by finding dense correspondences between a pair of images taken from two slightly different view angles. The disparities between these correspondences form a disparity map relative to the reference image, which contains depth information of the observed structure (1).

Among the most important factors of the correspondence problem are the metrics used to describe features of one point and compare the similarity between two potential matches in the presence of noise, the matching score. An ideal metric should be distinctive enough to find the correct match by capturing the most important features of each pixel while being invariant to view angles, illumination and reflectance variations, focus blur, and other deformations.

To describe the image or pixel features, a number of assumptions are usually made. Lambertian reflectance is assumed where image intensities of the same 3D point are the same regardless of the variations in the view angle [28]; local continuity is assumed where disparity values are generally continuous within a local neighborhood; frontoparallel surface orientation is assumed so that both image planes are identical and the corresponding 3D surface is frontoparallel to them [10].

Given two descriptors of a potential match, metrics commonly used to measure their similarity include sum of absolute or squared differences (SAD/SSD), normalized cross correlation (NCC) [6], and other more complex metrics such as mutual information [7], [15], [43]. To alleviate errors introduced by the support window, different kernels are introduced in evaluating the matching score, such as the Gaussian kernel, which decreases influences from pixels whose distances to the evaluated pixel is large. Color-weighted correlation uses kernels determined from both color and spatial differences [9].

2.2 Problems with Standard Assumptions

The assumption that corresponding pixels have the same intensity or color is only valid on surfaces with Lambertian reflectance [28]. When this assumption does not hold strictly or the intensity variations among neighboring pixels are not distinctive enough, intensity information within a neighborhood of the reference pixel can be aggregated for improved robustness. This aggregation implicitly requires a local continuity assumption assuming there is no geometric distortions between the corresponding neighborhoods from different views. To make the underlying assumptions more general, some approaches compute the surface normal and approximate the local region with a tangent plane [28]. Other approaches try to prevent the support window from covering object boundaries [30].

The stereo scenes of the Middlebury data sets typically consist of multiple piecewise planar objects [36] with Lambertian reflectance. For optimal performance, many of the current algorithms adopt a global optimization approach [25] with a matching metric derived from a single pixel intensity. These techniques formulate the disparity estimate as Markov Random Field (MRF) models, which involve minimizing an energy function E composed of a data term E_d and a smoothness term E_s [25]: E = E_d + λE_s. The linear data cost E_d is computed based on the intensity difference between a pair of pixels independently and the smoothness constraint is then involved as a part of the objective function E_s, which is optimized iteratively as messages of data costs pass around in the neighborhood. Segmentation is incorporated to fit regions with disparity planes. Finally, a balance is reached between each of the observed intensities and their spatial coherence [26]. Satisfactory results demonstrate their effectiveness since the disparity of each pixel is estimated by considering the 3D scene as a correlated structure instead of a set of independent point clouds. However, there are a number of factors that need further consideration.

First, the weight λ used to balance the data matching term E_d with the regularization term E_s is an important parameter in determining the energy function E and has to be estimated correctly. The optimal regularization parameter λ varies across different stereo pairs, which is related to the statistics of image noise and variations of scene structures [27].

Second, it is found that both graph cuts and loopy belief propagation (LBP) produced even lower energies than that of the ground truth data [25]. This indicates deviations of the underlying models and objective functions from the truth. Under the MRF framework, the smoothness term regularizes neighboring pixels to have similar disparities [21], region boundaries obtained from segmentation of intensity are assumed to coincide with depth discontinuities [22], and planar disparities are assigned to different regions [9].

Third, constraints enforced by surrounding pixels, supports from local neighborhood, and beliefs propagated from high confidence regions are all based on the same similarity measurement, i.e., the data term of the energy function. Most existing algorithms use simple data terms, such as SSD, SAD, or truncated absolute difference (TAD) of intensity between two pixels [27], to obtain an initial estimate which is then refined based on the same metric with an additional smoothness term. This simplification of the matching metric avoids difficulties in optimizing objective functions with several nonlinear terms [37]. For stereo pairs with non-Lambertian reflectance or other deformations, however, simple data terms only produce very noisy estimates on most of the pixels, which can hardly be improved by propagating beliefs from high confident regions to lower ones. If the pixel similarity itself is not measured correctly for a majority of correspondences, the messages passed around are not reliable. Therefore, we cannot expect any optimizations to correct those errors based on the same metric. Problems encountered under less ideal imaging conditions, such as imperfections of illumination, more challenging reflectance properties, and more complex structures, are seldom modeled because of the limitations of the energy formulation and the absence of the necessary data sets.

2.3 Motivation for Our Multiscale Approach

In image segmentation, Gaussian filter bank features, at a number of discrete scales and orientations, have been used successfully [1] because the responses to these filters express the information about a pixel and its surround better than simple pixel intensities at a single scale. Filter-based pixel feature vectors steered at various scales can extract features with a compact description that are discriminative and robust to noise. Matching ambiguities at low contrast or low texture regions can be resolved in scale space and the gradient components make it robust against deformations such as those caused by non-Lambertian reflectance.

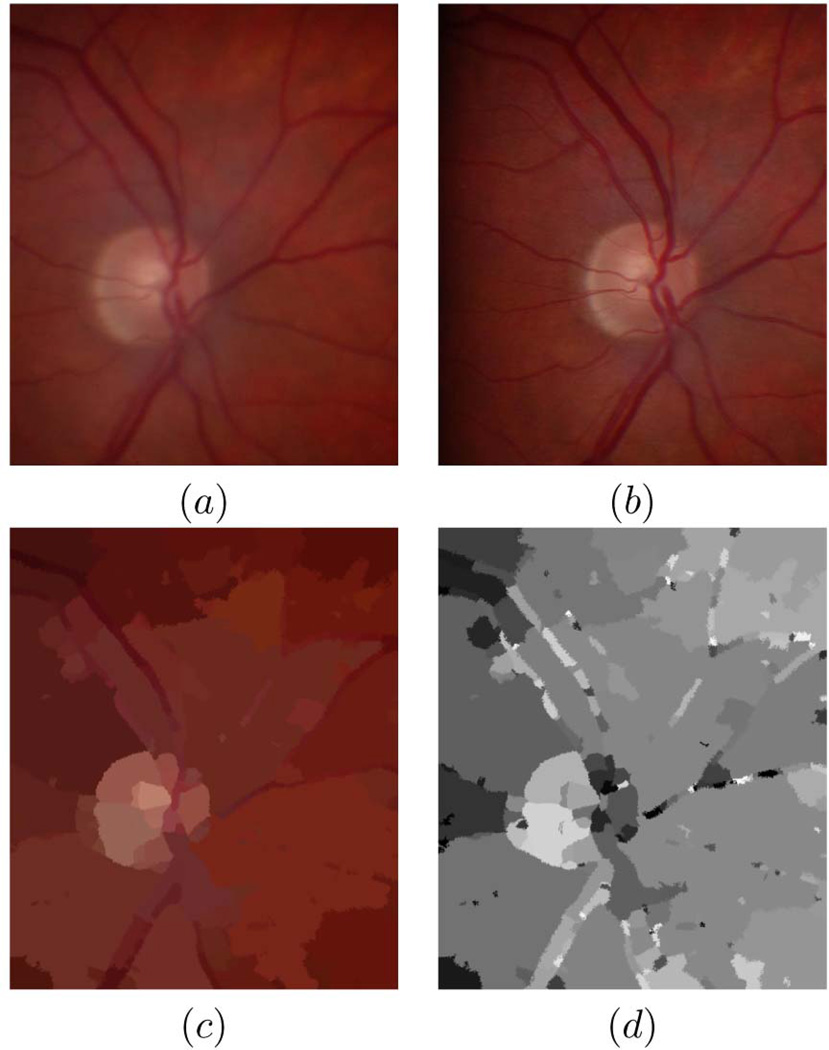
In this study, we develop a novel approach in order to handle depth from retinal stereo images with radiometric differences [38]. Fig. 1 shows a typical pair. Basically the retina is a continuous surface with a cup shaped region centered at the optic disc (see Fig. 6). Compared to the Middlebury data sets, stereo retinal images are challenging in different ways:

• The Lambertian reflectance model does not hold, as images do not show exactly the same intensities and hue from two view angles.

• Usually some parts of the images are blurred because photographers find it difficult to focus in both eyes at once.

• Most areas have little texture and the intensity boundaries do not always coincide with depth edges (see Figs. 1c and 1d).

• The cupping of the optic nerve causes severe foreshortening effects, which makes those regions have considerably different deformations in different images.

Fig. 1.

Typical retinal stereo images and problems with standard assumptions: (a) Left image, (b) right image, (c) segmentation according to image intensity, (d) disparity map obtained by a typical global optimization algorithm with piecewise planar surface assumption and brightness constancy assumption (Klaus et al. [8]).

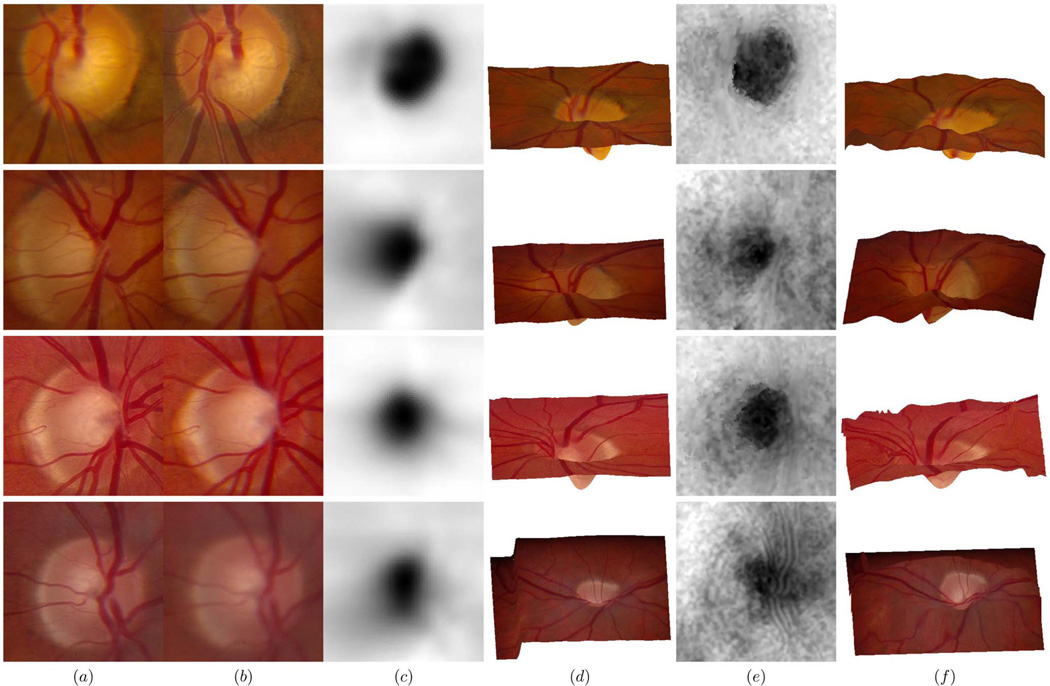
Fig. 6.

Comparison of four results obtained from the stereo fundus pairs and from the OCT scans: (a) Left fundus image centered at the optic disc, (b) right fundus image centered at the optic disc, (c) shape estimate of the optic nerve represented as grayscale maps from the OCT scans, (d) reference (left) image wrapping onto topography as output from the OCT scans, (e) shape estimate of the optic nerve represented as grayscale maps from the stereo fundus pairs, (f) reference (left) image wrapping onto topography as output from the stereo fundus pairs.

Among stereo correspondence literatures involving the scale space [11], [13], our algorithm is novel because we use a multiscale approach to describe both the pixel feature and the metrics for identification of correct match. In Section 3.2, the pixel feature is extracted by encoding the intensity of the reference pixel as well as its context, i.e., the intensity variations relative to its surroundings and information collected from its neighborhood, in the multiscale pixel feature vector. The matching score is described in Section 3.3, formulating the matching problem as the estimation of a continuous scale space evolution of disparity maps so that the paths through which different structures evolve across scales interact with each other and provide globally coherent disparity estimates. In combination, this novel approach can deal with radiometric differences, decalibration [42], limited illumination, noise, and low contrast or density of features.

3 Algorithm Description

3.1 Multiscale Framework

Scale space theory is closely related to neurophysiological and psychophysical findings in the human visual system [23] and is directly inspired by the physics of the observation process of grouping local properties into meaningful larger perceptual groups. Evidence shows that rapid, coarse percepts are refined over time in stereoscopic depth perception in the visual cortex [39]. We see from Fig. 1 that, for retinal stereo images with slowly varying texture, it is easier to associate a pair of matching regions from a global view as there are more prominent landmarks, such as blood vessels and the optic disc. On the other hand, given a limited number of candidate correspondences and the deformations in order to achieve correct matches between those landmarks, detailed local information is sufficient and more accurate to discern subtle differences among these candidates. This is the motivation of our multiscale framework, which is illustrated in Fig. 2 using a typical stereo fundus pair.

Fig. 2.

Disparity estimate process in scale space illustrated with a typical stereo fundus pair: (a) I₁(x, y, s_k) and I₂(x, y, s_k), (b) D(x, y, s_k), (c) D₀(x, y, s_k−1), (d) I₁(x, y, s_k−1) and I₂(x, y, s_k−1), (e) D(x, y, s_k−1).

On the left side of Fig. 2, the original stereo pair I₁(x, y) and I₂(x, y) is shown with two scales, s_k (Fig. 2a) and s_k−1 (Fig. 2d). The first row illustrates disparity representation at lower scale s_k. Given a pair of images I₁(x, y, s_k) and I₂(x, y, s_k) (Fig. 2a), a disparity map D(x, y, s_k) (Fig. 2b) is estimated at scale s_k and then up-scaled to D₀(x, y, s_k−1) (Fig. 2c), which matches the stereo pair I₁(x, y, s_k−1) and I₂(x, y, s_k−1) at higher scale s_k−1 (Fig. 2d). With constraints imposed by D₀(x, y, s_k−1), the disparity map evolves to the finer scale D(x, y, s_k−1) (Fig. 2e), which is shown as the second row of Fig. 2. This is the way the deep structure is represented in scale space. At each scale, certain features are selected as the salient ones, with a simplified and specified description [23].

3.1.1 Deep Structure Formation of Disparity Estimate

Scale space consists of image evolutions with the scale as the third dimension. The “deep” image structure along the scale axis is embedded hierarchically. To extract stereo pairs at different scales, a Gaussian function is used as the scale space kernel [3]. Many derivations of the front-end kernel all lead to the unique Gaussian kernel [23]. Image I_i(x, y) at scale s_k is produced from a convolution with the variable-scale Gaussian kernel G(x, y, σ_k), followed by a bicubic interpolation to reduce its dimension

$$I_i(x,y,s_k)={\varphi }_k[G(x,y,{\sigma }_k)*I_i(x,y),s_k]={\varphi }_k\left[\right(\frac{1}{2\pi {\sigma }_k^2}{e}^{-(x^2+y^2)/2{\sigma }_k^2})*I_i(x,y),s_k],i=1,2;x=1,\dots ,M_k;y=1,\dots ,N_k,$$ (2)

where symbol ⋆ represents convolution and ϕ_k(I, s_k) is the bicubic interpolation used to down-scale image I. The scales of neighboring images increase by a factor of r with a down-scaling factor: s_k = r^k, r > 1, k = K, K − 1, …, 1, 0. The resolution along the scale dimension can be increased with a smaller base factor r, which is set to 1.8 in our experiments. Parameter K is the first scale index which down-scales the original stereo pair to a dimension of no larger than M_min × N_min pixels, e.g., M_min = N_min = 16 in our implementation. The standard deviation σ_k of the variable-scale Gaussian kernel is proportional to the scale index k: σ_k = ck, where c = 1.2 is a constant related to the resolution along the scale dimension.

Similarly, scales of neighboring disparity maps also differ by a constant factor of r with the bicubic interpolation, following a 2D adaptive noise-removal Wiener filter. The low-pass Wiener filter estimates the local mean μ and variance σ² around each pixel in the disparity map D(x, y, s_k) within a squared neighborhood of w_k × w_k pixels and then creates output D₀(x, y, s_k−1) according to these estimates to smooth out noise [5]:

$$D_0(x,y,s_{k-1})={\varphi }_k^{\prime }[r·(\mu +\frac{{\sigma }^2-\overline{{\sigma }^2}}{{\sigma }^2}(D(x,y,s_k)-\mu )\left)\right],x=1,\dots ,M_{k-1};y=1,\dots ,N_{k-1},$$ (3)

where $\overline{{\sigma }^2}$ is the average of all the local estimated variances and ${\varphi }_k^{\prime }(·)$ is the bicubic interpolation used to upscale the estimated disparity map from scale s_k to scale s_k−1. The base factor r is introduced in (3) because each pixel in D(x, y, s_k) encodes the deformation information of r × r pixels in D₀(x, y, s_k−1). Let the dimension of D(x, y, s_k) be M_k × N_k at scale s_k. The size of the adaptive window w_k of the Wiener filter is a truncated linear function:

$$w_k=\mathit{\text{max}}(w_{\mathit{\text{min}}},\rho ·(M_k+N_k)),$$ (4)

where ρ is a constant which can be set to any reasonable values, e.g., 0.025 in our implementation, and w_min = 3 is the minimum size of the local filtering window.

The representation D₀(x, y, s_k−1) is intended to provide globally coherent search directions for the next finer scale s_k−1. Compared with passing messages around neighboring nodes in belief propagation [21], the multiscale representation provides a comprehensive description of the disparity map in terms of point evolution paths, which acts as the regularization component in our algorithm. Constraints enforced by landmarks guide finer searches toward correct directions along those paths while the small additive noise is filtered out. The Wiener filter performs smoothing adaptively, according to the local disparity variance. Therefore, depth edges in the disparity map are preserved where the variance is large and little smoothing is performed.

3.1.2 Resolve Matching Ambiguity in Scale Space

To identify correct correspondences, we specify the disparity range of a potential match, which is closely related to the computational complexity and desired accuracy. Under the multiscale framework, image structures are embedded along the scale dimension hierarchically. Constraints enforced by global landmarks are passed to finer scales as well-located candidate matches in a coarse-to-fine fashion. As locations of point S evolve continuously across scales, the link through them, L_S(s_k) : {I_S(s_k), k ∈ [0, K]}, could be predicted by the drift velocity [23], a first-order estimate of the change in spatial coordinates for a change in scale level. The drift velocity is related with the local geometry, such as the image gradient [23]. When the resolution along the scale dimension is sufficiently high, the maximum drift between neighboring scales can be approximated as a small constant δ for simplicity. Let the number of scale levels be N_s with base factor r, the maximum scale factor f_max = r^N_s. That is to say, a single pixel at the first scale accounts for a disparity drift of at least ±f_max pixels at the finest scale in all directions, which meets the requirements of our entire test data sets.

At scale s_k, given a pixel (x, y) in the reference image I₁(s_k) with disparity map D₀(x, y, s_k) passed from the previous scale s_k+1, locations of candidate correspondences S(x, y, s_k) in equally scaled matching image I₂(s_k) can be predicted according to the drift velocity Δ as

$$S(x,y,s_k)\in \{I_2(x+D_0(x,y,s_k)+\mathrm{\Delta },y,s_k)\},(x,y)\in I_1(x,y,s_k);\mathrm{\Delta }\in [-\delta ,\delta ].$$ (5)

A constant range δ of 1.5 for drift velocity worked well in our experiments. More accurate prediction can be achieved by adapting the drift velocity range δ to differential structures of the image [23]. The description of disparity D₀(x, y, s_k) not only guides the correspondence search toward the right directions along the point evolution path L, but also records the deformation information in order to achieve a match up to scale s_k+1. Given this description of the way image I₁(s_k+1) is transformed to image I₂(s_k+1) with deformation f(s_k+1) : I₁(s_k+1) → I₂(s_k+1), matching at scale s_k is easier and more reliable. This is how the correspondence search is regularized and propagated in scale space.

The test images of the stereo fundus pairs have disparities larger than 40 pixels (|D_max(x, y, s₀)| > 40) and the average disparity range (D_max(x, y, s₀) − D_min(x, y, s₀)) is around 20–30 pixels. The matching process has to assign one label (disparity value) to each pixel within this range. The multiscale approach essentially distributes this task to different scales so that, at each scale, the matching ambiguity is reduced significantly. This is extremely important for noisy stereo pairs with low texture density, as is the case in our experiments.

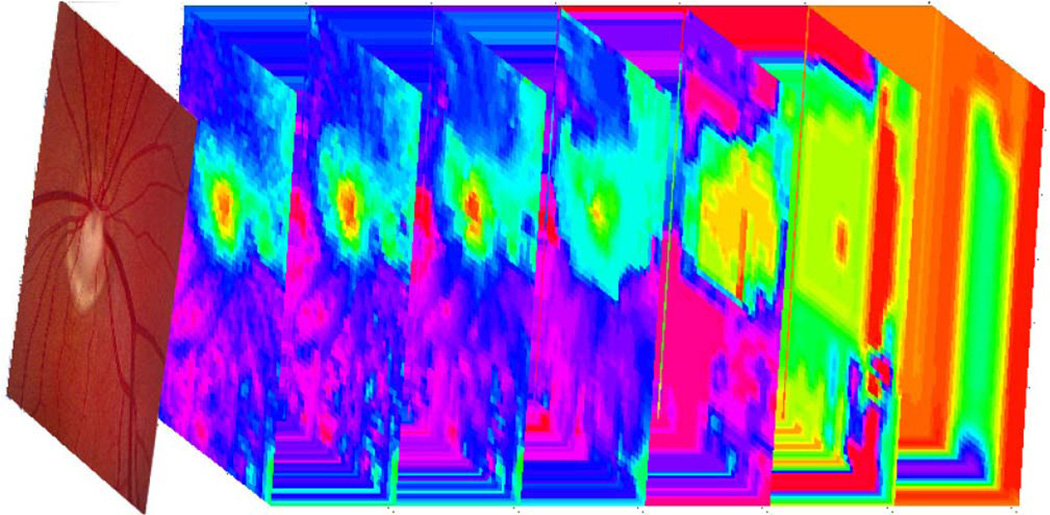
The deep structure formation of a disparity map with its evolution in scale space is illustrated in Fig. 3 with stereo fundus images. A stack of estimated disparity maps at seven scales is shown following the reference retinal image. The detailed structure of the optic disc is retrieved along the scale dimension. The formulation is consistent with the “perceptual grouping” performed by the human visual system, where comprehensive scene descriptions are formed from local features [23].

Fig. 3.

Deep structure formation of the disparity evolution in scale space with stereo fundus images.

Compared with the hierarchical algorithm proposed in [29], our scale space is produced with variable-scale Gaussian kernels based on the solution for the aperture function of the uncommitted visual front-end [23]. The description of the disparity map not only represents point evolution paths across scales but also deformations between the stereo pair up to the current scale. By dynamic programming proposed in [29], the sum of all costs of all matches is optimized in one scanline and an interscanline penalty was taken into account if there is no large vertical intensity gradient near the pixel under consideration. Our algorithm, in contrast, computes the matching cost over the two-dimensional image plane by taking advantages of the continuous behavior of the pixel feature vector in scale space, as described in the next section.

3.2 Multiscale Pixel Feature Vector

3.2.1 Composition of Multiscale Pixel Feature Vector

Performance of commonly used local image feature descriptors is evaluated in [4]. They showed that a second stage on top of low level descriptors [44], [45] is superior over single level detectors. SIFT-based descriptors (SIFT: scale invariant feature transform) [3] are a second stage built from low-level gradient kernels. They outperform other descriptors in spite of viewpoint change, image blur, and illumination variation [4], which are commonly perceived deformations in practical applications. Humans can binocularly fuse a stereo pair and perceive depth variations, regardless of these deformations, because the human visual system is more sensitive to the gradient of the intensity than its absolute magnitude [12]. Inspired by the gradient-based SIFT descriptor, our pixel feature vector [1] combines both intensity and gradient features of the pixel in scale space.

Furthermore, for low contrast images with slowly varying intensity and low texture density, it is hard to pick the right match based only on the intensity or gradient of a single pixel. Information provided by neighboring pixels has to be involved as the data component. The SIFT descriptor, which was originally proposed to detect distinctive feature points invariant to image scale and rotation [3], is a 3D histogram of gradient location and orientation, where location is quantized into a 4 × 4 location grid and the gradient angle is quantized into eight orientations [4]. This results in a descriptor of dimension 4 × 4 × 8 = 128. Alternatively, a larger gradient grid can be used and the dimension of the resulting vector is reduced with principal component analysis (PCA) [4].

As the spatial information is lost when representing local distribution of intensity gradients with a histogram, our pixel feature vector encodes the intensities, gradient magnitudes, and continuous orientations within the support window of a center pixel with their spatial location in scale space. The intensity component of the pixel feature vector consists of the intensities within the support window, as intensities are closely correlated between stereo pairs from the same modality. The gradient component consists of the magnitude and continuous orientation of the gradients around the center pixel. The gradient magnitude is robust to shifts of the intensity, while the gradient orientation is invariant to the scaling of the intensity [37], which exist in stereo pairs with radiometric differences.

3.2.2 Integration of Intensity Component and Gradient Component

Given pixel (x, y) in image I, its gradient magnitude m(x, y) and gradient orientation θ(x, y) of intensity are computed as follows:

$$m(x,y)=\sqrt{{[I(x+1,y)-I(x-1,y)]}^2+{[I(x,y+1)-I(x,y-1)]}^2},\theta (x,y)={\mathit{\text{tan}}}^{-1}\left[\frac{I(x,y+1)-I(x,y-1)}{I(x+1,y)-I(x-1,y)}\right].$$ (6)

The gradient component of the pixel feature vector F_g is the gradient angle θ weighted by the gradient magnitude m, which is essentially a compromise between the dimension and the discriminability

$${\mathbf{F}}_g(x_0,y_0,s_k)=[m(x_0-n_2,y_0-n_2,s_k)\times \theta (x_0-n_2,y_0-n_2,s_k),\dots m(x_0+n_2,y_0+n_2,s_k)\times \theta (x_0+n_2,y_0+n_2,s_k)].$$ (7)

Combined with the intensity component F_i:

$${\mathbf{F}}_i(x_0,y_0,s_k)=[I(x_0-n_1,y_0-n_1,s_k),\dots ,I(x_0,y_0-1,s_k),I(x_0,y_0,s_k),I(x_0,y_0+1,s_k),\dots ,I(x_0+n_1,y_0+n_1,s_k)],$$ (8)

the multiscale pixel feature vector F of pixel (x₀, y₀) is represented as the concatenation of both components:

$$\mathbf{F}(x_0,y_0,s_k)=[{\mathbf{F}}_i(x_0,y_0,s_k){\mathbf{F}}_g(x_0,y_0,s_k)],(x_i,y_j,s_k)\in N(x_0,y_0,s_k),$$ (9)

where the size of support window N(x₀, y₀, s_k) is (2n_i + 1) × (2n_i + 1) pixels, i = 1, 2. For intensity component and gradient component of the pixel feature vector, different sizes of supports can be chosen by adjusting n₁ and n₂, e.g., n₁ = 3 and n₂ = 4 in our implementation.

For low contrast images with slowly changing intensities, only a few key points have responses strong enough to be distinguished from others. In this case, the magnitude of intensity provides useful information, although it is not as robust as the gradient in noisy circumstances with intensity shifts. When there are clear features within the support window, the gradient orientation gives sensitive responses with continuous angles. A weight of the gradient magnitude puts more emphasis on those prominent features when giving their supports to the center pixel.

In scale space, both intensity dissimilarity and the number of features or singularities of a given image decrease as the scale becomes coarser [23]. At coarse scales, some features may merge together and intensity differences between stereo pairs become less significant, which make the intensity component of the pixel feature vector more reliable. At finer scales, one feature may split into several adjacent features, which requires gradient component for accurate localization. Though locations of different structures may evolve differently across scales, singularity points are assumed to form approximately vertical paths in scale space [23]. These can be located accurately with our scale invariant pixel feature vector. For regions with homogeneous intensity, the reliabilities of those paths are verified at coarse scales when there are some structures in the vicinity to interact with [35]. This also explains why the matching ambiguity can be reduced by distributing it across scales. With active evolution of the very features in the matching process, the deep structure of the images is fully represented due to the nice continuous behavior of the proposed pixel feature vector in scale space [23].

3.2.3 Comparison of Descriptor Discriminability

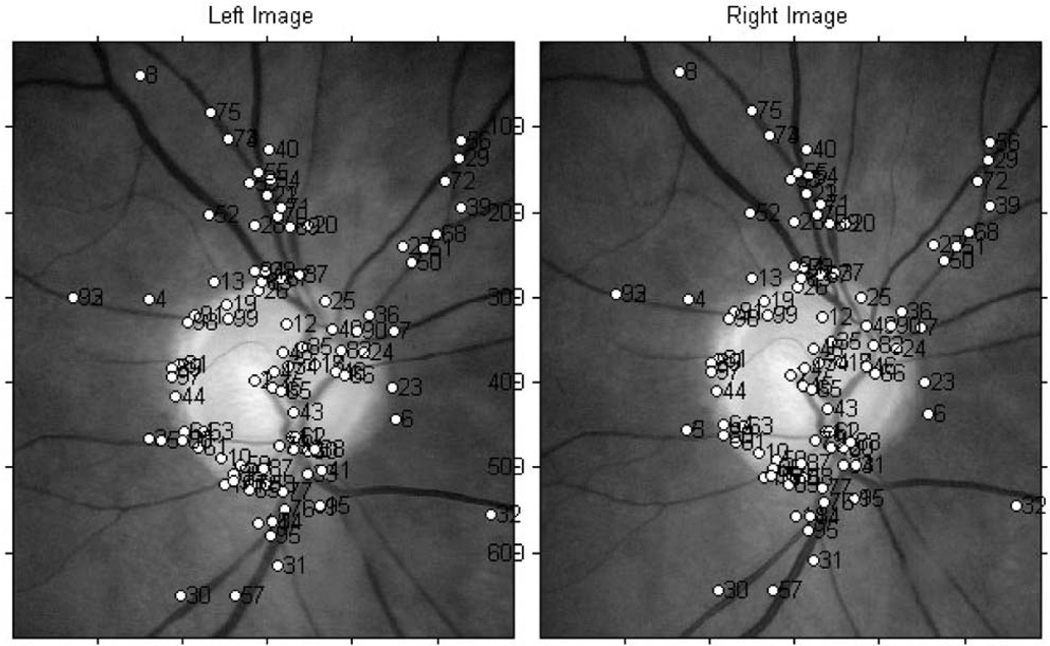
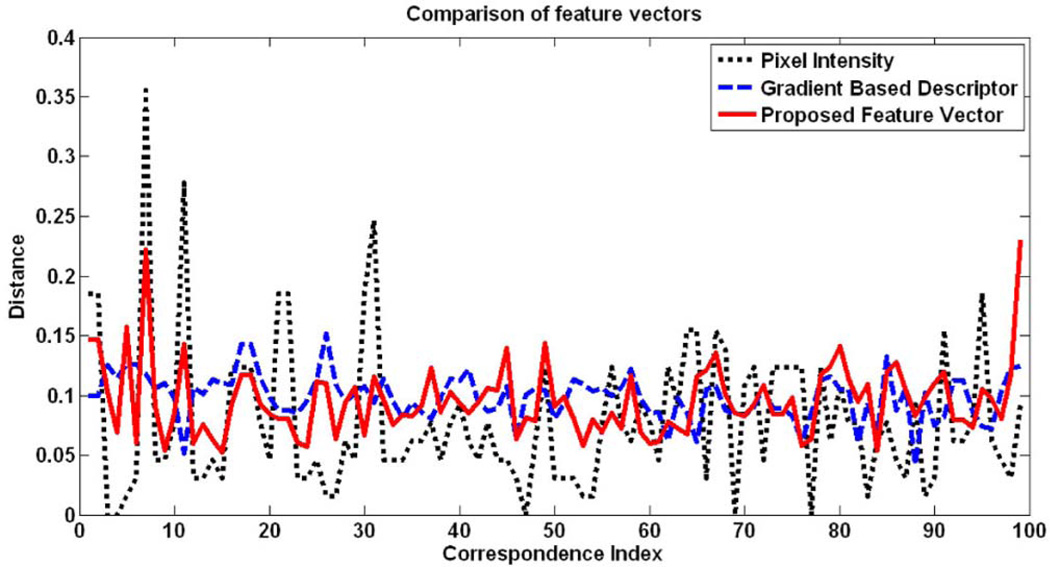
Fig. 4 shows a stereo fundus pair with 99 reliably matched correspondences at the finest scale. Three feature vectors of these correspondences are compared in Fig. 5, i.e., pixel intensity (F_I), gradient-based descriptor (F_G), and the proposed multiscale pixel feature vector (F_S). The pixel intensity vector F_I is a one-dimensional feature of the intensity of that pixel and the gradient-based descriptor F_G is a grid of gradient orientation with their spatial locations around the center pixel.

Fig. 4.

A stereo fundus pair with 99 reliably matched correspondences.

Fig. 5.

Comparison of three feature vectors.

For a pair of correspondences with index i, each of those three features forms two vectors ${\mathbf{F}}_1^i\text{ and }{\mathbf{F}}_2^i$ extracted from the stereo pair. The euclidean distance of the two corresponding vectors is computed as

$${\mathrm{\Delta }}_i={\Vert {\mathbf{F}}_1^i-{\mathbf{F}}_2^i\Vert }_2,$$

followed by a normalization:

$${\mathrm{\Delta }}_i={\mathrm{\Delta }}_i/{\Vert \mathrm{\Delta }\Vert }_2,i=1,\dots ,99.$$

Here, ‖x‖₂ is the euclidean length of a vector x. In Fig. 5, the x-axis represents index i and the y-axis represents euclidean distance Δ_i.

For those correct matches, distances between a pair of feature vectors are supposed to be consistently small. Compared with gradient-based descriptor F_G and the proposed pixel feature vector F_S, pixel intensity F_I has large variations across the stereo pair. The mean and standard deviation (SD) of these three curves are listed in Table 1, which show that the proposed pixel feature vector F_S is resistant to noise, regardless of texture density. Given one point $p_1^i$ in the left image and a matching criterion, the third row of Table 1 shows the number of correctly identified correspondences in the vicinity of point $p_2^i$ in the right image within a search region of 11 pixels. The proposed pixel feature vector F_S is more discriminative than the other two, even measured with the simple euclidean distance, and hence is what we used in our multiscale framework.

TABLE 1.

Comparison of Three Feature Vectors

	FI	FG	FS
Mean	5.1313	1.1713	0.4485
SD	4.0220	0.2278	0.1442
Correct Matches	5	8	32

3.3 Matching Score in Scale Space

Given two pixel feature vectors describing characteristics of a potential matching pair, the matching score is used to measure the degree of similarity between them and determine if the pair is a correct match.

3.3.1 Matching Score Based on Disparity Evolution

As we formulate the matching metric in scale space, deformations of the structure available up to scale s_k+1 are encoded in the disparity description D₀(x, y, s_k), which can be incorporated into a matching score based on disparity evolution in scale space. Specifically, those pixels with approximately the same drift tendency during disparity evolution as the center pixel (x₀, y₀) within its support window N(x₀, y₀, s_k) provide more accurate supports with less geometric distortions. Hence, they are emphasized even if they are spatially located far away from center pixel (x₀, y₀). This is performed by introducing an impact mask W(x₀, y₀, s_k), which is associated with the pixel feature vector F(x₀, y₀, s_k) in computing the matching score

$$\mathbf{W}(x_0,y_0,s_k)=\mathit{\text{exp}}[-\alpha |D_0(x,y,s_k)-D_0(x_0,y_0,s_k)|],(x,y,s_k)\in N(x_0,y_0,s_k).$$ (10)

Parameter α = 1 adjusts the impact of pixel (x, y) according to its current disparity distance from pixel (x₀, y₀) when giving its support at scale s_k. The matching score r₁ is then computed between pixel feature vectors F₁(x₀, y₀, s_k) in the reference image I₁(x, y, s_k) and one of the candidate correspondences F₂(x, y, s_k) in the matching image I₂(x, y, s_k) as

$$r_1({\mathbf{F}}_1(x_0,y_0,s_k),{\mathbf{F}}_2(x,y,s_k))=\frac{{\displaystyle {\sum }_N}(\mathbf{W}·{\mathbf{F}}_1(x_0,y_0,s_k)-{\mathrm{F̄}}_1)(\mathbf{W}·{\mathbf{F}}_2(x,y,s_k)-{\mathrm{F̄}}_2)}{\sqrt{\sum {(\mathbf{W}·{\mathbf{F}}_1(x_0,y_0,s_k)-{\mathrm{F̄}}_1)}^2\sum {(\mathbf{W}·{\mathbf{F}}_2(x,y,s_k)-{\mathrm{F̄}}_2)}^2}},(x,y,s_k)\in S(x_0,y_0,s_k),$$ (11)

where F̄_i is the mean of the pixel feature vector after incorporating the deformation information available up to scale s_k+1. The way that image I₁(s_k+1) is transformed to image I₂(s_k+1) is also expressed in the matching score through the impact mask W(x₀, y₀, s_k) and propagated to the next finer scale.

The support window is kept constant across scales as its influence is handled automatically by the multiscale formulation. At coarse scales, the aggregation is performed within a large neighborhood comparative to the scale of the stereo pair. Therefore, the initial representation of the disparity map is smooth and consistent. As the scale moves to finer levels, the same aggregation is performed within a small neighborhood comparative to the scale of the stereo pair. So, the deep structure of the disparity map appears gradually during the evolution process with sharp depth edges preserved. Actually, there are no absolutely “sharp” edges. It is a description relative to the scale of the underlying image. A sharp edge at one scale may appear smooth at another scale.

3.3.2 Identification of Correspondences in Scale Space

To account for out-of-focus blur as is commonly observed in stereo imaging (refer to Fig. 1), the search for a correct match is not only performed among pixels with different spatial locations but also among pixels located in the neighboring scales. Given reference image I₁(x, y, s_k), a set of neighboring variable-scale Gaussian kernels {G(x, y, σ_k+Δk)} is applied to matching image I₂(x, y):

$$G(x,y,{\sigma }_{k+\mathrm{\Delta }k})*I_2(x,y),\mathrm{\Delta }k\in [-\epsilon ,+\epsilon ].$$ (12)

The feature vector of pixel (x₀, y₀) is extracted in the reference image as F₁(x₀, y₀, s_k) and in the neighboring scaled matching images (12) as F₂(x, y, s). The point associated with the maximum matching score (x, y)^* is taken as the correspondence for pixel (x₀, y₀), where subpixel accuracy is obtained by fitting a polynomial surface to matching scores evaluated at discrete locations within the search space of the reference pixel S(x₀, y₀, s_k) with the scale as its third dimension

$${(x,y)}^{*}=\mathit{\text{arg max}}(r_1({\mathbf{F}}_1(x_0,y_0,s_k),{\mathbf{F}}_2(x,y,s))),(x,y,s)\in S(x_0,y_0,s_k).$$ (13)

The process of finding the maximum matching score among neighboring scales is inspired by the SIFT-based key point detection, where the local extrema is obtained by comparing in neighborhoods both in the current image and in the scale above and below the current one [3]. This step essentially measures similarities between pixel (x₀, y₀, s_k) in reference image I₁ and candidate correspondences (x, y, s) in matching image I₂ in scale space [35]. Due to the limited DOF of the optical sensor, two equally scaled retinal stereo images may actually have different scales with respect to structures of the retina, which may cause inconsistent movements of the singularity points in scale space. Therefore, when we search for correspondences, we jointly find the best matched spatial location and the best matched scale.

3.3.3 Fusion of Symmetric Estimates

To treat the stereo pair equally at each scale, both left image I₁(x, y, s_k) and right image I₂(x, y, s_k) are used as the reference in turn to get two disparity maps, D₁(x, y, s_k) and D₂(x, y, s_k), which satisfy

$$I_{1(2)}(x,y,s_k)=I_{2(1)}(x+D_{1(2)}(x,y,s_k),y,s_k),(x,y)\in I_{1(2)}(x,y).$$ (14)

As D_i(x, y, s_k), i = 1, 2 has subpixel accuracy; for those evenly distributed pixels in the reference image, their correspondences in the matching image may fall in between of the sampled pixels. When the right image is used as the reference, correspondences in the left image are not distributed evenly in pixel coordinate. To fuse both disparity maps and produce one estimate relative to left image I₁(x, y, s_k), a bicubic interpolation is applied to get a warped disparity map $D_2^{\prime }(x,y,s_k)$ from D₂(x, y, s_k), which satisfies

$$I_1(x,y,s_k)=I_2(x+D_2^{\prime }(x,y,s_k),y,s_k),\text{where }{D}_2^{\prime }(x+D_2(x,y,s_k),y,s_k)=-D_2(x,y,s_k).$$ (15)

The matching score r₂(x, y, s_k) corresponding to D₂(x, y, s_k) is warped to $r_2^{\prime }(x,y,s_k)$ accordingly. Since both disparity maps D₁(x, y, s_k) and $D_2^{\prime }(x,y,s_k)$ represent disparity shifts relative to the left image at scale s_k, they can be merged together to produce a fused disparity map D(x, y, s_k) by selecting disparities with larger matching scores.

4 Experiments

Our proposed algorithm, as described above, was evaluated by comparing its performance quantitatively (if available) and qualitatively with top ranked algorithms at the Middlebury stereo vision benchmark (http://vision.middlebury.edu/stereo/eval/), if an implementation was available to us:

• (currently ranked first) a segment-based algorithm by Klaus et al., which assigns a disparity plane to each segmented region based on reliably matched correspondences [8] (coded by Shawn Lankton);

• (ranked third) an energy-minimization algorithm by Yang et al., with color-weighted correlation, hierarchical belief propagation, and occlusion handling [9] (executable code provided by the author);

• (not yet ranked) a variational algorithm by Brox et al. which implements the nonlinearized optical flow constraint used in image registration and can deal with images with radiometric differences and decalibration [37] (coded by Visesh Chari);

• (not ranked) conventional correlation, which was added as a baseline algorithm.

The parameters of our proposed algorithm were fixed for all images in all experiments except on the standard Middlebury data set, where a smaller base factor r = 1.2 was used to increase the resolution along the scale dimension. Large images were rescaled to 500–800 pixels in a preprocessing step for computational efficiency.

4.1 Quantitative Performance Analysis on Stereo Fundus Images

4.1.1 Data Collection and Evaluation Criterion

We compared our proposed algorithm and the top ranked algorithms quantitatively on a data set of 30 pairs of stereo fundus images. Color stereo photographs of the optic disc and spectral domain optical coherence tomography (SD-OCT) images of the ONH from 34 patients were obtained at the Glaucoma Clinic at the University of Iowa. Color slide stereo photographs centered on the optic disc of both eyes were acquired using a fixed-base Nidek 3D× digital stereo retinal camera. The stereo images were down-scaled to 768 × 1,019 pixels by automatically locating the optic disc in the 4,096 × 4,096 images [16]. The cropped images, as is shown in Fig. 1, included the optic disc in its entirety in all images. SD-OCT scans were acquired using a Cirrus OCT scanner in the 200 × 200 × 1,024 mode. Surfaces of the retinal layer were detected in the raw OCT volume using 3D segmentation [17], [18], [19], [20]. Depth information was recorded as intensities and registered manually with the reference stereo photographs to provide ground truth for performance evaluation.

The accuracy of the disparity map as output by our algorithm is measured by the root of mean squared (RMS) differences E_RMS between the estimate and the ground truth. To exclude those nonoverlapping regions and focus only on the main structure—cupping of the optic nerve—both maps are cropped to 251 × 251 pixels centered at the optic disc for comparison.

4.1.2 Comparison with Results Obtained from OCT Scans

Fig. 6 compares four results obtained from the stereo fundus pairs and from the OCT scans. Columns (a) and (b) show the cropped stereo fundus images centered at the optic disc. Columns (c) and (e) are the estimated shape of the optic nerve represented as grayscale maps within the same region. Columns (d) and (f) show the reference image (the central part shown as Fig. 6a) wrapping onto topography as output from the stereo fundus images and from the OCT scans. A smoothing filter is applied to both results before 3D surface wrapping. By binocularly fusing the stereo pairs (a), (b) and comparing it to the results obtained from the OCT scans (c), (d), we also verified that the shape information provided by the OCT scans is accurate and it is registered with the reference fundus image correctly.

The cupping of the optic nerve is correctly estimated from stereo fundus images (see Table 2). There are intensity inconsistencies between these pairs as well as different degrees of blur, especially in the last example (the original stereo pair is shown in Fig. 1). If we align and switch back and forth between the left and the right images, we can also observe clear geometric deformations from separate view angles. Satisfactory results are obtained in spite of these challenging conditions. As disparities between the last stereo pair are large, no shape information can be retrieved in the nonoverlapping regions.

TABLE 2.

RMS Error Comparison of Estimates on 30 Pairs of Stereo Fundus Images

RMS Error	Our Algorithm	Klaus et al. [8]	Brox et al. [37]	Correlation
Mean	0.1592	2.9174	0.8260	1.3254
SD	0.0879	6.6328	0.8508	1.3327
95% CI	0.1264 – 0.1920	0.4406 – 5.3941	0.5083 – 1.1436	0.8277 – 1.8230

Errors occur (for example, in some regions on the last row of Figs. 6e and 6f) when features present in the stereo pair are significantly different.

4.1.3 Comparison with Results Obtained from Other Algorithms

We applied the other four algorithms to our stereo fundus data sets and measured the RMS differences E_RMS with the results obtained from OCT scans. The mean E_RMS of the 30 estimates shows the superiority of our algorithm (0.1592 (95 percent CI 0.1264–0.1920)) over others in Table 2. As for the algorithm proposed by Yang et al. [9], it applies segmentation several times with different parameters to get from oversegmented to undersegmented regions. If the parameters are all kept the same as those used for the Middlebury data set, most regions get very similar disparities (see Fig. 8b), probably due to the low texture density in the fundus images. Since we are not sure how to determine the optimal parameter settings, we did not measured its RMS differences with the results obtained from the OCT scans. RMS error for conventional correlation was not especially large compared to other more sophisticated algorithms because we set exact disparity ranges manually for each of the 30 fundus pairs. The error was computed within regions centered at the optic disc (Figs. 6a and 6b), where the contrasts were relatively high.

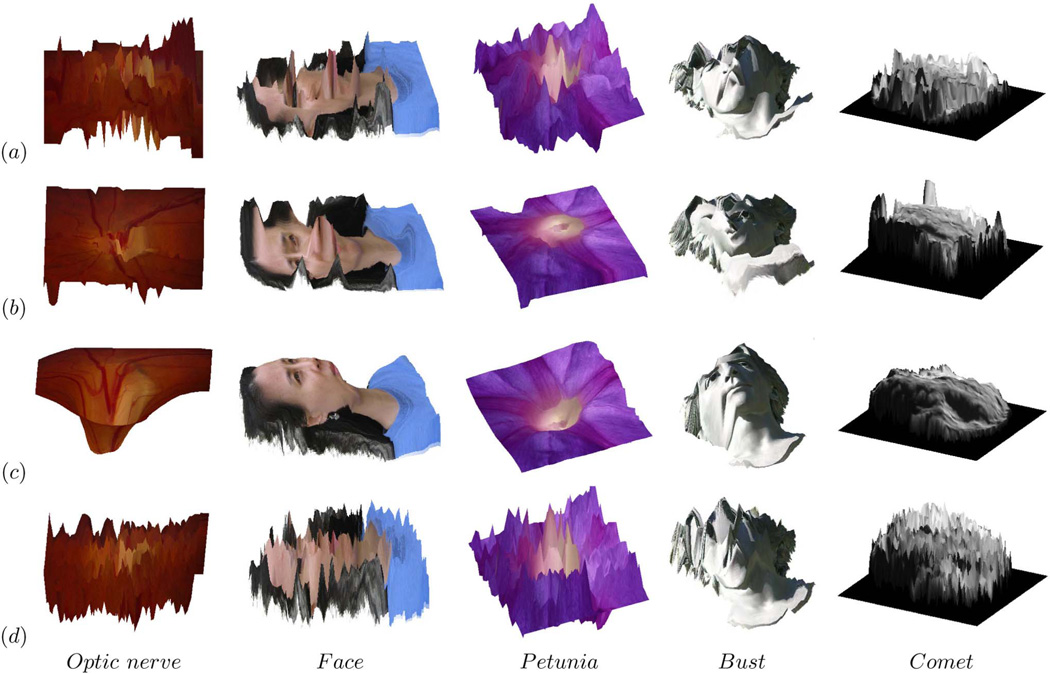
Fig. 8.

Displays left image wrapped to topography based on disparity estimates (same images as in Fig. 7) but this time using the disparity maps obtained by top ranking depth-from-stereo algorithms and conventional correlation, from left to right, optic nerve head (second row of Fig. 6), face, petunia (http://pinker.wjh.harvard.edu/photos/stereo%20flowers/index.htm), bust (http://www.bke.org/Bayreuth2005/CosimaHeadStereo.htm) and comet (http://stardust.jpl.nasa.gov/news/news97.html): (a) Klaus et al. [8], (b) Yang et al. [9], (c) Brox et al. [37], (d) conventional correlation.

4.2 Face Validity Evaluation on Other Publicly Available Stereo Data of Isolated Objects

4.2.1 Application of Our Approach to Nonfundus Data Sets

The issues with fundus images described in this paper are also found in other images, especially faces and statues of faces. Therefore, we also tested our algorithm on a variety of other stereo pairs that are available publicly to evaluate its performance. Due to the absence of ground truth data for these stereo pairs, results for these images can be assessed qualitatively only.

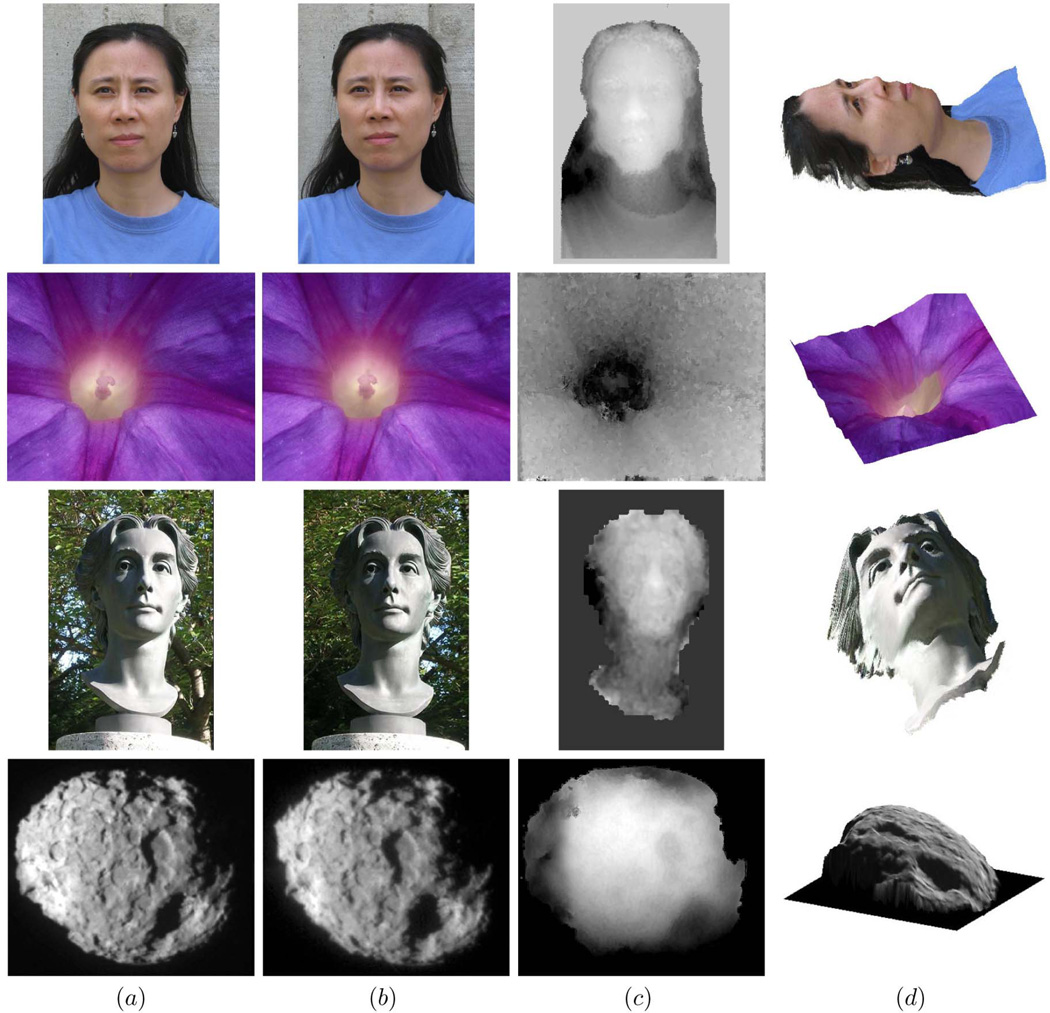
The first stereo pair (Figs. 7a and 7b) was taken by ourselves with a hand held digital camera. There are plenty of regions with low texture density, such as those on the plain T-shirt. The disparity estimates are represented as grayscale maps (see Fig. 7c), where darker regions represent larger distances from the camera. We see that not only the face itself, but also the round neck of the T-shirt as well as wrinkles on the shoulder are assigned coherent disparity values.

Fig. 7.

Disparity estimates obtained by our proposed algorithm on publicly available stereo data lacking ground truth, from top to bottom, face (taken by ourselves), petunia (http://pinker.wjh.harvard.edu/photos/stereo%20flowers/index.htm), bust (http://www.bke.org/Bayreuth2005/CosimaHeadStereo.htm), and comet (http://stardust.jpl.nasa.gov/news/news97.html): (a) Left image, (b) right image, (c) grayscale coding of disparity estimate, (d) left image wrapped to topography based on disparity estimate.

The second pair was obtained, with permission, from Dr. S. Pinker’s website with stereo photographs of flowers (http://pinker.wjh.harvard.edu/photos/stereo%20flowers/index.htm). The matching ambiguity was resolved correctly by distributing it through scale space. Most pixels in this set have similar hue. The trumpet shape of the petunia is clearly perceived from the reconstructed 3D surface (see Fig. 7d). The elevated center part is distinct and the five deeper strips can also be distinguished in the surrounding regions. This example demonstrates that our algorithm can deal with depth discontinuities and discriminate small depth variations.

The third stereo pair, of a bust of composer Richard Wagner’s wife, available at http://www.bke.org/Bayreuth2005/CosimaHeadStereo.htm, was taken in bright sunlight, casting crisp and dark shadows on half of the face. The intensities are not consistent across the stereo pair, but the estimated shape of the face is symmetric between the dark half and the bright half of the face.

The last stereo pair shows the nucleus of comet 81P/Wild 2 taken by NASA’s Stardust spacecraft in 2004, available at http://stardust.jpl.nasa.gov/news/news97.html. Its disparity range is large, with both positive and negative disparities. There are clear geometric distortions caused by separate view angles. The features and textures on the nucleus surface are not very distinct, with some blur. The overall shape of the nucleus and its rough surface are estimated properly, with several large depressed regions visible.

4.2.2 Performance of Other Algorithms on These Nonfundus Data Sets

Fig. 8 displays the same topography wrapped images, but this time using the disparity estimates from four other algorithms, illustrating the generality of the problem. Stereo images of the retina typically do not satisfy brightness constancy assumptions and have weakly textured and out-of-focus regions. While top ranked algorithms have nearly perfect performance on the standard Middlebury data set, they clearly do much less well on these widely available images which violate such assumptions.

The energy minimization algorithm by Klaus et al. [8] segments images to small regions and assigns continuous disparities to each of them: The depth edges are preserved quite well between different regions and, at the same time, the depth surface is smooth within each region, which are good for estimating disparities in images with clear boundaries and consistent intensities, especially if depth discontinuities coincide with intensity edges. If the images do not fit this specific model, the results may deviate from the truth considerably. The algorithm by Yang et al. [9], another optimization algorithm with linear data terms, also produces errors when similar assumptions are violated, such as piecewise planer surfaces and intensity constancy. The factor used to balance the data term and the regularization term, as well as the parameters involved in segmentation is image dependent. By employing higher order constancy assumptions, the optic flow algorithm by Brox et al. [37] is tolerant of noise and demonstrates reasonable overall performance on our data set. But it has a tendency to oversmooth the structure and lose some details of depth variations. As for conventional correlation, it is resistant to intensity inconsistencies to some extent. But, at regions of low contrast and low texture density, it is not discriminative enough to resolve the matching ambiguities.

We also tested our algorithm on the standard Middlebury data sets [2], [36]. The average percentage of bad pixels (disparity error larger than 1) in our algorithms was high (18.7) compared with segmentation-based optimization approaches. Qualitative evaluation shows that most errors occur on small foreground objects with large disparities compared with the scale of the stereo pair, such as the narrow lamp neck in the Tsukuba pair (384 × 288 pixels with a disparity range of 0–15 pixels).

5 Conclusion AND Discussions

We have developed a novel multiscale stereo matching algorithm to find reliable dense correspondences between fundus images which contain radiometric differences, and showed our algorithm qualitatively outperforms top ranked algorithms on stereo pairs of isolated objects that exhibit non-Lambertian reflectance. We were able to confirm these results quantitatively on our data set of stereo retinal images. Our results show that algorithms that perform well on the Middlebury data sets exhibit markedly lower performance on data sets where the assumptions in the Middlebury data sets do not hold. Specifically, experiments on the optic disc reconstruction using 30 test stereo fundus pairs had a mean RMS error of 0.1592 and an SD of 0.0879, while the algorithm that ranked first on the Middlebury benchmark when this paper was last reviewed, Klaus et al. [8], had a mean RMS error of 2.9174 and a SD of 6.6328.

Obviously, the Middlebury data sets are geared toward understanding relative depths of objects in scenes, which is useful, for example, in computer vision applications for collision avoidance. However, in our experience and in our opinion, 3D shape from medical stereo images with radiometric differences deserves at least as much attention from depth-from-stereo research groups. However, they are currently underrepresented in existing standard test data sets, leading away from good performance on such stereo problems. As algorithm designs are more and more driven by the available test data sets, inclusion of such medical stereo data sets will be important to move the field forward by expanding its versatility, and to be more representative for various stereo vision problems. We offer to share our data sets with other researchers to advance the field under entirely different scenarios on noisy medical images originating from practical applications. Our data sets do not suffer some of the implicit idiosyncrasies of the data sets at the Middlebury website—though introducing some of their own.

The approach we chose in this study has several drawbacks. Primarily, it ranks low on the standard Middlebury data sets evaluation ranking because it does not handle occlusions and narrow foreground objects explicitly. Specifically, the “narrow foreground objects” are relative to the scale of the images. Our proposed algorithm takes advantage of the continuous behavior of the deep structure evolution in scale space, and if the scale of the images is not sufficient to show a continuous evolution process of those small objects, evolution of the singularity points and structures may produce different paths as they separate and merge with each other. The way occluded features interact with their vicinities and affect the predictions of accurate disparity estimate along the scale dimension remains to be investigated. Because it is implemented in Matlab, it takes over 1 hour per stereo pair to produce both horizontal and vertical disparity maps simultaneously, and we are currently working on a more efficient version in a compiled language.

Deformations between image patches associated with the same 3D point, caused by surface reflectance properties under less ideal but constant imaging conditions, are commonly observed in many real world applications, including in the examples we show. Specifically, registrations of different retinal modalities have been proposed [40], [41], but such problems are different because corresponding scene elements in our images are still correlated without dramatic changes in overall intensity distributions.

In summary, our proposed algorithm shows both qualitative and quantitative superior performance in finding reliable dense correspondences in low contrast medical stereo images with radiometric differences, with little texture or noticeable imaging noise, compared to existing algorithms that model objects as piecewise planar surfaces with distinct features and perfect reflectance properties. Under the multiscale framework, geometric regularizations are imposed by rich descriptors instead of constraints obtained from region segmentation. Salient features selected at certain scales are encoded in the pixel feature vector to describe interactions of different structures in terms of point evolution paths. Disparity is assigned not only by comparing candidate correspondences with different spatial locations but also among points located in the neighboring scales. Deep structures of the scene are revealed as continuous evolution of disparity estimates across the scale space, which resolves the matching ambiguity efficiently by distributing it through the scale dimension to provide globally coherent estimates. We expect that algorithms such as the one presently proposed have potential applications for robust shape-from-stereo beyond medical images.

Biographies

Li Tang is an assistant research scientist in ophthalmology and visual sciences at the University of Iowa. Her research interests include image analysis/processing, computer vision, and pattern recognition.

Mona K. Garvin received the BSE degree in biomedical engineering in 2003, the BS degree in computer science in 2003, the MS degree in biomedical engineering in 2004, and the PhD degree in biomedical engineering in 2008, all from the University of Iowa. She is an assistant professor in the Department of Electrical and Computer Engineering at the University of Iowa. She is also affiliated with the Iowa Institute for Biomedical Imaging and the VA Center of Excellence for the Prevention and Treatment of Visual Loss. Her research interests include medical image analysis and ophthalmic imaging. She is a member of the IEEE and the IEEE Computer Society.

Kyungmoo Lee received the PhD degree from the University of Iowa in 2009 and is currently an assistant research engineer in the Department of Electrical and Computer Engineering at the same university. His specialty is medical image processing and analysis including segmentations of intraretinal layers, optic discs, and retinal blood vessels from optical coherence tomography (OCT) images. He is a student member of the IEEE.

Wallace L.M. Alward is a professor of ophthalmology at the University of Iowa and holds the Frederick C. Blodi Chair in Ophthalmology. His primary research interests are molecular genetics of glaucoma, pigmentary glaucoma, and diagnostic methodologies.

Young H. Kwon is the Clifford M. & Ruth M. Altermatt Professor of Ophthalmology at the University of Iowa specializing in glaucoma. He splits time between clinical work and imaging research on glaucoma patients.

Michael D. Abràmoff received the MD degree from the University of Amsterdam in 1994 and the PhD degree in 2001 from the University of Utrecht, The Netherlands. He is an associate professor of ophthalmology and visual sciences at the University of Iowa, Iowa City, with joint appointments in the Electrical and Computer Engineering and Biomedical Engineering Departments. He is an associate director of the US Department of Veterans Affairs Center of Excellence for the Prevention and Treatment of Visual Loss. He serves on the American Academy of Ophthalmology and the Iowa Medical Society. When he is not seeing patients with retinal disease or teaching medical students, residents, and fellows, he oversees a highly successful retinal image analysis research program. His focus is on automated early detection of retinal diseases, image guided therapy of retinal disease, and computational phenotype-genotype association discovery. He holds seven patents and patent applications in this field. He is an associate editor of the IEEE Transactions on Medical Imaging. He is a senior member of the IEEE.