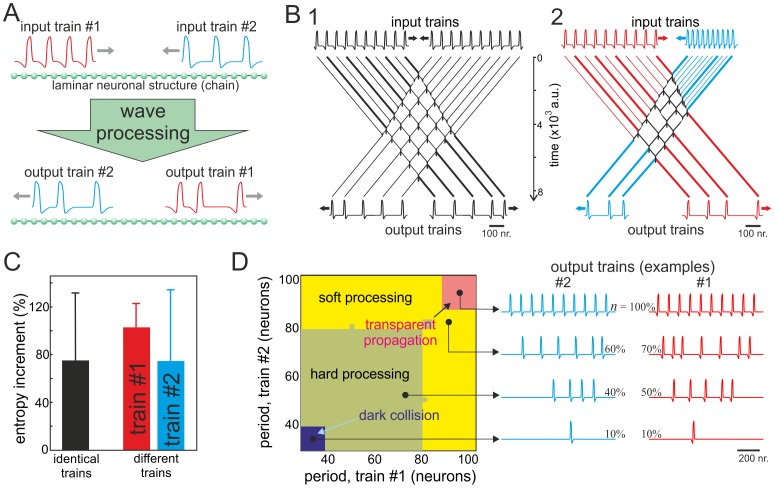
Figure 6. Wave-processing of periodic wave trains: Complexity resonance.
A) Sketch of numerical experiments. Two input periodic wave trains (#1 and #2) are injected from both ends of the chain modeling laminar neuronal structure (gray arrows indicate direction of propagation). Nonlinear interaction of the trains, i.e. the wave-processing, leads to two emerging output trains with different aperiodic structure. B) Representative examples of collisions of identical periodic trains (left panel: 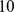 waves, spatial period
waves, spatial period 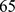 neurons) and trains with different spatial periods (right panel: 10 waves, spatial periods
neurons) and trains with different spatial periods (right panel: 10 waves, spatial periods 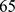 and
and 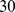 neurons). Evolution of the wave crests shows how the interplay between symmetric and asymmetric wave collisions yields aperiodic output trains. Waves propagating to the output are drawn by thicker lines. C) Entropy increment provided by the wave-processing of identical and different periodic trains (means and standard deviations). For identical trains periods from
neurons). Evolution of the wave crests shows how the interplay between symmetric and asymmetric wave collisions yields aperiodic output trains. Waves propagating to the output are drawn by thicker lines. C) Entropy increment provided by the wave-processing of identical and different periodic trains (means and standard deviations). For identical trains periods from 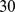 to
to 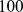 neurons have been considered. For different trains the period of the input train #1 was kept constant (
neurons have been considered. For different trains the period of the input train #1 was kept constant (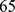 neurons), while the period of the input train #2 spanned interval from
neurons), while the period of the input train #2 spanned interval from 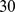 to
to 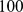 neurons. D) Complexity resonance. Left panel: colored regions mark four types of wave-processing. Right panel: Examples of output trains for each type of the wave-processing. Complexity of the output trains reaches maximum at intermediate spatial periods of input trains (
neurons. D) Complexity resonance. Left panel: colored regions mark four types of wave-processing. Right panel: Examples of output trains for each type of the wave-processing. Complexity of the output trains reaches maximum at intermediate spatial periods of input trains (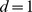 ,
, 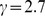 ).
).