Table 4. Multivariable logistic regression model for schizophrenia.

Covariate	Coefficient (SE)	Test Statisticsa	P-valueb	Odds Ratio (95% CI)
Intercept	10.20(2.05)	24.68	<0.001
Gating	1.00(0.48)	4.28	0.039	2.72(1.05–7.00)
d’	−0.37(0.22)	2.69	0.101	0.69(0.45–1.07)
Arithmetic	−0.32(0.10)	9.91	0.002	0.73(0.60–0.89)
Block Design	0.28(0.14)	3.99	0.046	1.32(1.01–1.74)
Performance IQ	−0.19(0.03)	13.66	0<.001	0.90(0.86–0.95)
Smoke	1.58(.80)	3.88	0.049	4.87(1.01–23.5)

SE: standard error; CI: confidence interval.

Gating is defined as a dichotomous variable: P50 gating ratio greater than 0.4 or not.

Smoke is defined as a dichotomous variable: smoking or not.

^a Wald chi-square tests.

^b P-values were 2-sided.

Multivariable logistic regression model: n  = 160, percentage of concordant pairs  = 90.4%, percentage of discordant pairs  = 9.6%, c statistic  = 0.9043, Hosmer-Lemeshow Goodness-of-Fit test p  = .640>.05 (df  = 8).

The estimated probability of having schizophrenia (the predicted value, 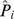) can be obtained by using the following formula:

where Gating equals 1 if P50 gating ratio >0.4, and 0 otherwise; Smoke equals 1 if smoking, and 0 otherwise.