Table 4. Power estimated in the simulation study (1−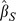 ) and using the Cramer-Rao’s bound (1−
) and using the Cramer-Rao’s bound (1−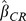 ) for different values of the sample size in each group (
) for different values of the sample size in each group (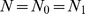 ), the group effect (
), the group effect ( ), the variance of the latent variable (
), the variance of the latent variable (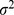 ), the spacing regularity of the items and the gap between the global mean of the latent variable and the mean of the distribution of the item difficulties (
), the spacing regularity of the items and the gap between the global mean of the latent variable and the mean of the distribution of the item difficulties (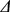 ).
).
| Normal distribution | Mixture of normal distributions | |||||||

|
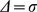
|
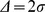
|

|
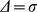
|
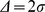
|
|||
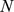
|

|
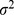
|
1−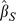 1− 1−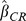
|
1−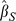 1− 1−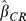
|
1−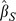 1− 1−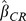
|
1−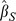 1− 1−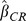
|
1−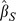 1− 1−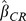
|
1−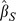 1− 1−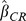
|
| 50 | 0.2 | 0.25 | 0.224/0.219 | 0.222/0.213 | 0.225/0.196 | 0.206/0.218 | 0.228/0.214 | 0.209/0.198 |
| 1 | 0.133/0.123 | 0.129/0.118 | 0.109/0.105 | 0.118/0.122 | 0.125/0.119 | 0.133/0.108 | ||
| 4 | 0.052/0.066 | 0.060/0.064 | 0.061/0.057 | 0.064/0.065 | 0.069/0.064 | 0.071/0.059 | ||
| 9 | 0.077/0.050 | 0.064/0.048 | 0.069/0.045 | 0.061/0.049 | 0.056/0.049 | 0.067/0.046 | ||
| 0.5 | 0.25 | 0.849/0.790 | 0.849/0.829 | 0.845/0.789 | 0.841/0.817 | 0.857/0.829 | 0.866/0.792 | |
| 1 | 0.513/0.513 | 0.493/0.488 | 0.425/0.420 | 0.513/0.508 | 0.472/0.495 | 0.421/0.437 | ||
| 4 | 0.198/0.203 | 0.197/0.192 | 0.192/0.157 | 0.226/0.201 | 0.210/0.196 | 0.202/0.168 | ||
| 9 | 0.115/0.119 | 0.142/0.112 | 0.121/0.095 | 0.129/0.118 | 0.114/0.115 | 0.120/0.103 | ||
| 0.8 | 0.25 | 0.999/0.991 | 0.997/0.996 | 0.997/0.993 | 0.998/0.994 | 0.997/0.996 | 0.998/0.993 | |
| 1 | 0.899/0.887 | 0.878/0.868 | 0.801/0.803 | 0.886/0.884 | 0.888/0.874 | 0.822/0.820 | ||
| 4 | 0.446/0.439 | 0.441/0.412 | 0.418/0.329 | 0.418/0.434 | 0.433/0.423 | 0.458/0.357 | ||
| 9 | 0.273/0.237 | 0.225/0.222 | 0.257/0.179 | 0.243/0.235 | 0.230/0.229 | 0.248/0.197 | ||
| 100 | 0.2 | 0.25 | 0.401/0.393 | 0.414/0.381 | 0.400/0.349 | 0.385/0.391 | 0.420/0.381 | 0.422/0.352 |
| 1 | 0.208/0.205 | 0.208/0.195 | 0.183/0.169 | 0.199/0.202 | 0.201/0.197 | 0.188/0.176 | ||
| 4 | 0.086/0.093 | 0.098*/0.090 | 0.108/0.078 | 0.097/0.093 | 0.088/0.091 | 0.094/0.082 | ||
| 9 | 0.072/0.064 | 0.084*/0.062 | 0.067/0.056 | 0.080/0.064 | 0.057/0.063 | 0.079/0.059 | ||
| 0.5 | 0.25 | 0.988/0.984 | 0.987/0.985 | 0.988/0.975 | 0.989/0.985 | 0.988/0.985 | 0.984/0.977 | |
| 1 | 0.831/0.809 | 0.795/0.782 | 0.711/0.707 | 0.822/0.802 | 0.788/0.788 | 0.743/0.729 | ||
| 4 | 0.361/0.359 | 0.376*/0.338 | 0.361/0.270 | 0.334/0.355 | 0.353/0.346 | 0.327/0.292 | ||
| 9 | 0.217/0.195 | 0.204*/0.183 | 0.192/0.150 | 0.198/0.193 | 0.212/0.188 | 0.197/0.164 | ||
| 0.8 | 0.25 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | |
| 1 | 0.994/0.995 | 0.993/0.992 | 0.985/0.980 | 0.991/0.994 | 0.990/0.993 | 0.984/0.983 | ||
| 4 | 0.720/0.725 | 0.723*/0.693 | 0.722/0.577 | 0.718/0.719 | 0.725/0.705 | 0.714/0.616 | ||
| 9 | 0.399/0.421 | 0.422*/0.394 | 0.453/0.312 | 0.430/0.418 | 0.412/0.406 | 0.415/0.348 | ||
| 200 | 0.2 | 0.25 | 0.695*/0.671 | 0.682/0.654 | 0.663/0.609 | 0.641*/0.664 | 0.679/0.653 | 0.683/0.612 |
| 1 | 0.364/0.363 | 0.356/0.345 | 0.281/0.296 | 0.362/0.356 | 0.331/0.347 | 0.303/0.307 | ||
| 4 | 0.141/0.146 | 0.159/0.139 | 0.153/0.116 | 0.152/0.144 | 0.143/0.141 | 0.148/0.123 | ||
| 9 | 0.095/0.091 | 0.087/0.087 | 0.095/0.075 | 0.102/0.090 | 0.100/0.088 | 0.124/0.080 | ||
| 0.5 | 0.25 | 1.000*/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000*/1.000 | 1.000/1.000 | 1.000/1.000 | |
| 1 | 0.984/0.980 | 0.973/0.974 | 0.939/0.945 | 0.973/0.978 | 0.980/0.974 | 0.951/0.953 | ||
| 4 | 0.616/0.620 | 0.609/0.588 | 0.638/0.482 | 0.627/0.613 | 0.609/0.599 | 0.655/0.515 | ||
| 9 | 0.341/0.343 | 0.327/0.321 | 0.343/0.256 | 0.352/0.341 | 0.365/0.331 | 0.354/0.284 | ||
| 0.8 | 0.25 | 1.000*/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000*/1.000 | 1.000/1.000 | 1.000/1.000 | |
| 1 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | ||
| 4 | 0.942/0.951 | 0.959/0.937 | 0.948/0.864 | 0.946/0.949 | 0.935/0.942 | 0.941/0.891 | ||
| 9 | 0.696/0.702 | 0.703/0.667 | 0.691/0.549 | 0.692/0.698 | 0.700/0.683 | 0.709/0.602 | ||
| 300 | 0.2 | 0.25 | 0.838/0.838 | 0.831/0.824 | 0.831/0.785 | 0.835/0.832 | 0.822*/0.822 | 0.839/0.787 |
| 1 | 0.481/0.505 | 0.490/0.483 | 0.419/0.416 | 0.494/0.496 | 0.518/0.484 | 0.447/0.430 | ||
| 4 | 0.231/0.198 | 0.170/0.187 | 0.191/0.153 | 0.188/0.195 | 0.178/0.190 | 0.204/0.164 | ||
| 9 | 0.096/0.116 | 0.125/0.110 | 0.102/0.093 | 0.109/0.115 | 0.130/0.112 | 0.104/0.100 | ||
| 0.5 | 0.25 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000*/1.000 | 1.000/1.000 | |
| 1 | 0.997/0.998 | 0.998/0.998 | 0.994/0.992 | 0.998/0.998 | 0.998/0.998 | 0.992/0.994 | ||
| 4 | 0.806/0.792 | 0.803/0.762 | 0.781/0.650 | 0.821/0.786 | 0.795/0.773 | 0.794/0.688 | ||
| 9 | 0.444/0.478 | 0.479/0.449 | 0.467/0.358 | 0.471/0.475 | 0.490/0.462 | 0.492/0.398 | ||
| 0.8 | 0.25 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000*/1.000 | 1.000/1.000 | |
| 1 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | ||
| 4 | 0.993/0.993 | 0.995/0.990 | 0.994/0.963 | 0.991/0.993 | 0.994/0.991 | 0.993/0.975 | ||
| 9 | 0.859/0.862 | 0.843/0.834 | 0.862/0.723 | 0.851/0.859 | 0.858/0.847 | 0.851/0.776 | ||
| 500 | 0.2 | 0.25 | 0.969/0.968 | 0.964/0.963 | 0.968/0.945 | 0.972/0.965 | 0.963/0.962 | 0.959/0.946 |
| 1 | 0.701/0.722 | 0.681/0.697 | 0.632/0.619 | 0.705/0.712 | 0.721/0.698 | 0.662/0.636 | ||
| 4 | 0.306/0.299 | 0.310/0.282 | 0.283/0.227 | 0.289/0.295 | 0.305/0.288 | 0.279/0.244 | ||
| 9 | 0.151/0.165 | 0.162/0.155 | 0.178/0.128 | 0.171/0.164 | 0.169/0.159 | 0.163/0.140 | ||
| 0.5 | 0.25 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | |
| 1 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | ||
| 4 | 0.962/0.948 | 0.949/0.932 | 0.949/0.857 | 0.953/0.945 | 0.957/0.938 | 0.952/0.885 | ||
| 9 | 0.715/0.692 | 0.679/0.657 | 0.673/0.540 | 0.704/0.688 | 0.685/0.672 | 0.686/0.594 | ||
| 0.8 | 0.25 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | |
| 1 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | 1.000/1.000 | ||
| 4 | 1.000/1.000 | 1.000/1.000 | 1.000/0.998 | 1.000/1.000 | 1.000/1.000 | 1.000/0.999 | ||
| 9 | 0.975/0.976 | 0.975/0.966 | 0.975/0.909 | 0.968/0.975 | 0.979/0.971 | 0.979/0.939 | ||
Results for a questionnaire composed of 10 items.
The 95% confidence interval of the type I error does not contain the expected value of 5%.
