Probabilistic framework for assessing the ice sheet contribution to sea level change

Abstract

Previous sea level rise (SLR) assessments have excluded the potential for dynamic ice loss over much of Greenland and Antarctica, and recently proposed “upper bounds” on Antarctica’s 21st-century SLR contribution are derived principally from regions where present-day mass loss is concentrated (basin 15, or B15, drained largely by Pine Island, Thwaites, and Smith glaciers). Here, we present a probabilistic framework for assessing the ice sheet contribution to sea level change that explicitly accounts for mass balance uncertainty over an entire ice sheet. Applying this framework to Antarctica, we find that ongoing mass imbalances in non-B15 basins give an SLR contribution by 2100 that: (i) is comparable to projected changes in B15 discharge and Antarctica’s surface mass balance, and (ii) varies widely depending on the subset of basins and observational dataset used in projections. Increases in discharge uncertainty, or decreases in the exceedance probability used to define an upper bound, increase the fractional contribution of non-B15 basins; even weak spatial correlations in future discharge growth rates markedly enhance this sensitivity. Although these projections rely on poorly constrained statistical parameters, they may be updated with observations and/or models at many spatial scales, facilitating a more comprehensive account of uncertainty that, if implemented, will improve future assessments.

Quantifying the future rate of sea level rise (SLR) is critical for climate change mitigation and coastal planning efforts (1–4). However, the requirements for precision and robustness in SLR projections depend on the specific objectives, location, risk tolerance, and time horizon of decision makers (1, 4–7). A comprehensive risk management approach to sea level change would thus be greatly aided by a continuous probabilistic representation that allows the likelihood of upper bounds (i.e., SLR with a minimal chance of exceedance) to be generated and assessed self-consistently with best estimates (2, 4, 7).

Although probabilistic projections have been made for other sources of SLR (e.g., thermosteric expansion; refs. 8, 9) and other climate indicators (e.g., climate sensitivity; ref. 10), the contribution of continental ice sheets to SLR has generally been presented without an associated likelihood (2, 3, 8, 11). The development of probabilistic projections with process-based numerical ice sheet models is hindered by persistent physical uncertainties and computational constraints (8, 12, 13).

In the absence of comprehensive, process-based, models, ice sheet mass loss has been projected using expert-informed regional mass balance scenarios (3, 11). In these scenarios, the future Antarctic SLR contribution is almost entirely derived from Pine Island and Thwaites glaciers [where present-day mass loss is concentrated (14–17)] despite evidence that future discharge in other drainage basins remains uncertain. This evidence includes: (i) observations of ongoing dynamic change (17), (ii) the possibility of substantial changes in climatic boundary conditions (18, 19), and (iii) evidence that other basins may have contributed to previous episodes of SLR (20, 21). The ice loss scenarios of refs. 11 and 3 are presented without a probability of exceedance, making the relevance of excluded regions, and the interpretation of their upper bounds, problematic.

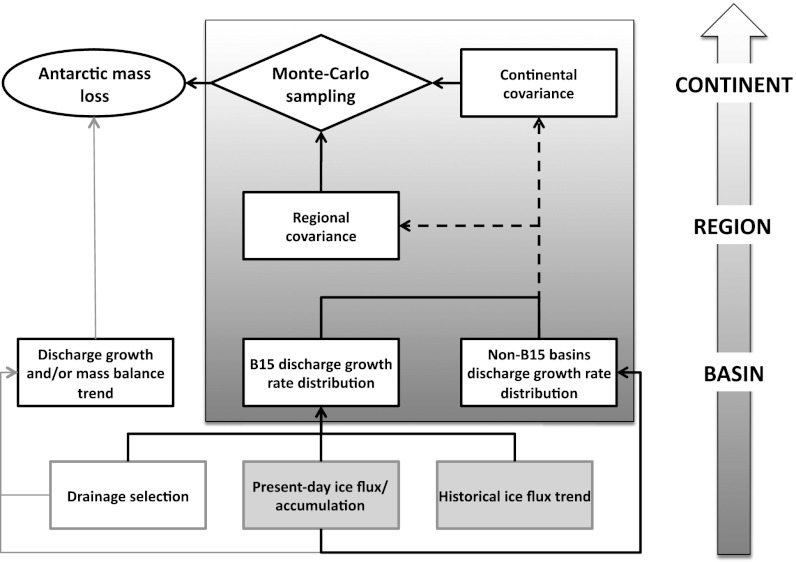
In this paper, we present a probabilistic framework in which Antarctic mass loss is calculated as the sum of regional contributions that are linked via statistical relationships (schematically illustrated, as applied in this paper, in Fig. 1). Including uncertainty in present-day and future discharge clarifies the quantitative impact of different subsets of drainage basins. With an upper bound defined by explicit exceedance probability, we highlight the uncertainties that dominate upper-bound SLR projections, so that these uncertainties may be systematically reduced by targeted observations and process-based modeling. We conclude with suggestions for future extensions of this framework.

Fig. 1.

Schematic of the methodology used in this paper, with black arrows illustrating the process, and the probabilistic component highlighted in the shaded box. Dashed lines indicate an either/or choice of covariance structure, and observations are shown in boxes with a grey background. For comparison, the process used in previous scenario-based SLR projections (3, 11) is shown with gray arrows.

1. Setting Up the Problem

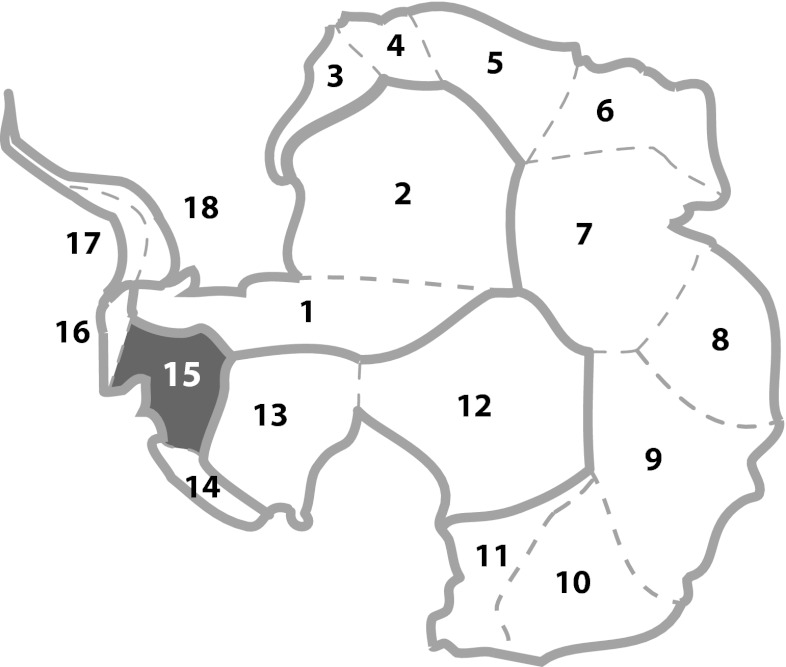
We first segregate Antarctica into 18 major drainage basins (after ref. 15; Fig. 2). In each basin (b), we use a mass balance model in which accumulation (A⁰, in GT y⁻¹) remains constant and discharge (Q, in GT y⁻¹) grows continuously with a constant rate (α_b). This discharge growth rate is applied to a baseline discharge (Q⁰) in the year t⁰:

Fig. 2.

Eighteen drainage basins (b) for which mass balance projections are calculated separately. Thin, dashed outlines indicate basin divides; thick outlines indicate the regions (r) of the ice sheet over which discharge growth rates are correlated in this analysis. Non-B15 West Antarctic basins include basins 1, 13, 14, and 16–18. See Table 1 for more details.

 To account for uncertainty in Antarctica’s present-day mass balance (15, 16), we incorporate observational baselines (i.e., A⁰ and Q⁰) from two different analyses, here referred to as R08 (14) and Z11 (15) (Fig. 2 and Table 1). Uncertainty in future discharge is propagated to SLR projections by Monte Carlo (MC) sampling of α_b from a multivariate normal distribution where α ∼ ₁₈(μ, Σ) (selected other distributions are presented in Fig. S1). In the remainder of this section, we describe the various α examined in this analysis; more details are available in Materials and Methods.

Table 1.

Baseline accumulation (A²⁰⁰⁰) and discharge (Q²⁰⁰⁰) in the 18 basins (b) and 5 regions (r) of the ice sheet in this analysis

		Accumulation		Discharge
r	b	R08	Z11	R08	Z11
1: Weddell Sea
	1	165	165	169	155
	2	100	100	81	78
2: East Antarctica
	3	50	50	53	49
	4	32	32	33	30
	5	62	62	62	60
	6	115	115	116	63
	7	87	87	91	83
	8	137	137	148	125
	9	261	261	270	222
	10	136	136	138	109
	11	62	62	65	33
3: Ross Sea
	12	89	89	76	54
	13	130	130	96	87
4: Amundsen Sea
	14	128	44	151	144
	15	196	159	260	247
	16	71	53	120	111
5: Antarctic Peninsula
	17	77	58	84	82
	18	157	157	178	178

Basin boundaries (and numerical identifier) are defined according to table 4 in ref. 15 (Z11), except basin 16 (corresponds to 16.1), basin 17 (corresponds to 16.2), and basin 18 (corresponds to 17).

In basin 15 (B15), distributions for discharge growth rates [(μ₁₅, σ²₁₅)] are generated by fitting trends in observed discharge (22) to Eq. 1 with n = 0.5, 1.0, and 2.0 (square root, linear, and quadratic laws, respectively). Our choice to extrapolate historic trends is driven principally by weak constraints on B15’s future mass balance. However, ice sheets adjust slowly to climate forcing; their future SLR contribution will, to some degree, reflect an ongoing dynamic response to historic perturbations (20, 23). Furthermore, although changes in B15 discharge are not driven by a specific climate forcing or emissions scenario, they are largely consistent with process-based regional and continental-scale ice sheet model simulations (24–26).

Discharge growth rate distributions may be uniquely specified for non-B15 basins; however, data are limited for many basins, and specifying statistical parameters at this level of detail obscures this analysis. Instead, we assume discharge growth is temporally constant, linear (n = 1.0), has a zero mean (μ_b = 0), and is equally uncertain across non-B15 basins. To aid the physical interpretation of the variance, we present uncertainty in non-B15 basin discharge growth as a fraction of the historical mean growth rate of B15. For example, with σ_b = 0.5μ₁₅, a non-B15 basin has a less than 3% chance of experiencing 100-y sustained discharge growth rates greater than B15’s 30-y linear trend (22).

Ice discharge in different basins may be linked via internal dynamics or shared boundary conditions. Here, two plausible statistical representations of spatially correlated discharge growth are examined by assigning a correlation coefficient at a regional (ρ_r) or a continental scale (ρ_a). Regions are roughly designated by the continental shelf seas into which discharge occurs. This correlation structure represents an assumption that regional oceanic forcing is a trigger for dynamic change (17). A continental correlation implies larger-scale linkages, perhaps due to changes in surface air temperatures and precipitation, or widespread ocean warming (19).

The sensitivity of SLR projections to discharge originating outside of B15 is assessed by performing MC simulations with different σ_b, ρ_r, and ρ_a for aggregations of basins in West Antarctica (WA) and the entire Antarctic ice sheet (ALL) (Fig. 2).

2. Results

2.1. B15 Contribution to Sea Level.

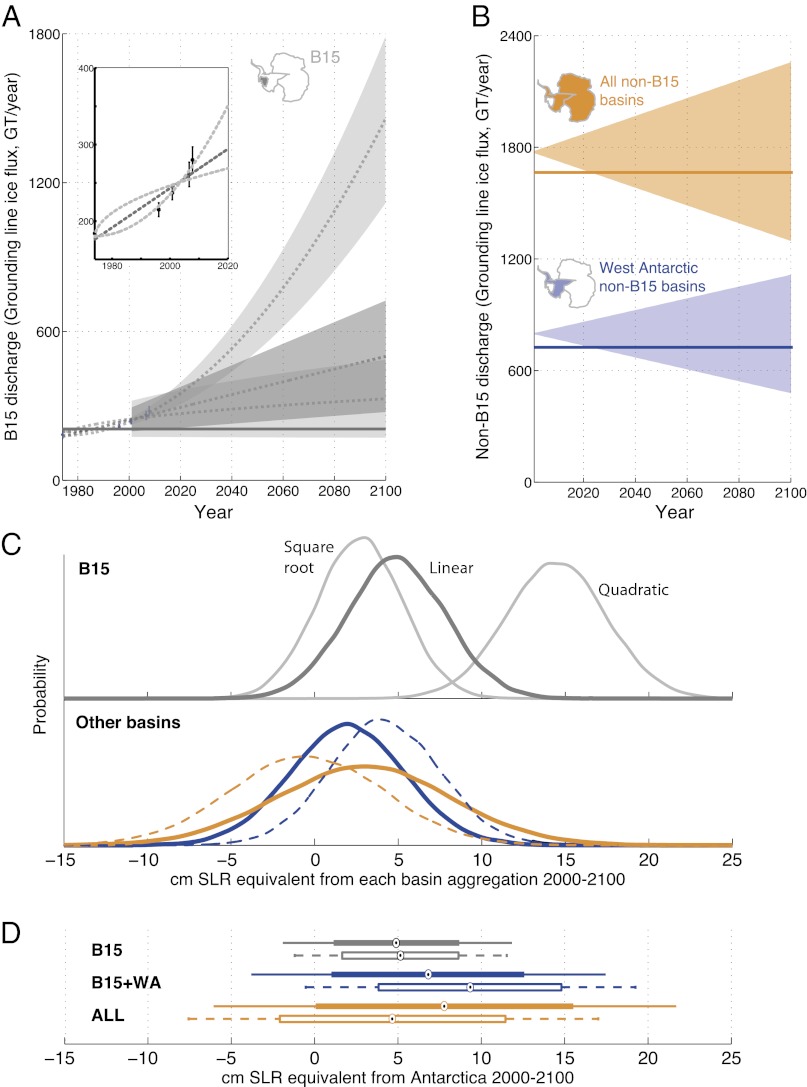
With constant accumulation, extrapolations of B15 discharge (Fig. 3A) give a median 2000–2100 SLR projection of ∼5 cm for a linear discharge growth law (dark gray lines in Fig. 3 C and D) and 3 and 14 cm for square root and quadratic laws, respectively (light gray lines). The spread of SLR projections is broadened by uncertainty in the fit (for example, a linear extrapolation gives a 10th–90th-percentile range of 1.1–8.7 cm). However, the nature of the growth law, particularly if quadratic growth is plausible, is the dominant uncertainty examined here. Although the Z11 and R08 baselines differ, the effect of these datasets on projections of B15 is small due to offsetting differences in accumulation and discharge (Table 1).

Fig. 3.

Discharge projections and sea level contribution for B15 and non-B15 basins. In A, dashed lines show fits to linear (dark gray) and square root and quadratic (light gray) growth laws. The 10th to 90th percentile range for each growth law over the period of extrapolation is shown with shading (Materials and Methods). In B, 2000–2100 10th–90th-percentile ranges of discharge are shown for non-B15 WA basins and all non-B15 basins using the R08 baseline (σ_b = 0.5μ₁₅ = 0.73% y⁻¹). Solid lines show the present-day accumulation (196 GT y⁻¹ for B15, 924 GT y⁻¹ for non-B15 WA basins, and 1,866 GT y⁻¹ for all non-B15 basins). (C) Probability distributions of 2000–2100 Antarctic sea level contribution for B15 (gray lines), non-B15 WA basins (blue), and all non-B15 basins (orange). Dashed lines use the Z11 baseline. In D, box plots show the probability distribution using (solid) R08 and (hollow) Z11 baselines for B15, WA and B15, and all Antarctic basins. Circles indicate the median SLR projection, thick lines show 10th–90th-percentile ranges, and whiskers extend to the 1st- and 99th-percentile SLR outcome.

2.2. Non-B15 Contribution to Sea Level.

When non-B15 basins are subject to an uncertain dynamic response, they increase SLR projections by: (i) translating the SLR distribution toward higher values, if discharge growth rates are positive or the present-day mass balance is negative, and (ii) widening the spread of the SLR distribution, if discharge growth rates are uncertain. The contribution of non-B15 basins is isolated in Fig. 3C, using the R08 (solid) and Z11 (dashed) baselines, with σ_b = 0.5μ₁₅ and no spatial correlation in discharge growth rates.

Median projections.

Because non-B15 basins are assumed to have normally distributed, zero-centered, discharge growth rates, their contribution to median SLR (−0.1 to 4.0 cm) is a 100-y continuation of any present-day mass imbalance and is determined by the choice of observational baseline (Fig. 3C). Both observational baselines indicate mass loss is dominated by drainage basins in the Antarctic Peninsula and the Amundsen Sea Sector (basins 15–18); the WA simulations (blue lines) thus result in a comparable (R08)—or higher (Z11)—median 2100 SLR than the ALL simulations (orange lines). With the Z11 baseline, median SLR is almost doubled (∼9 cm) by extrapolations of present-day mass losses in WA, yet the large positive present-day mass balance of East Antarctic basins in Z11 offsets WA ice loss. East Antarctic basins exhibit a slightly negative mass balance in R08, resulting in a 3-cm (60%) higher median SLR projection for the entire ice sheet if R08 is used as a baseline.

Upper-bound projections.

The choice of the exceedance probability that corresponds to an upper bound is subjective; here; we discuss outcomes with a 10% and 1% chance of exceedance (the endpoints of the whiskers in Fig. 3D), noting that 1% may be significantly higher than the flood protection mandates of some end-users of SLR projections (27). These probabilities bracket the upper bound of the “very likely” range used by the Intergovernmental Panel on Climate Change (95th percentile/5% chance of exceedance; ref. 28).

If only B15 is included, a linear growth rate is assumed, and a 10% chance of exceedance is chosen to represent the upper bound, the Antarctic SLR contribution is ∼8.7 cm (filled gray box in Fig. 3D). Using the R08 baseline and σ_b = 0.5μ₁₅, this upper bound increases to 12.6 cm when all of WA’s basins (blue lines) or to 15.5 cm if the entire ice sheet (ALL, orange lines) is included. A lower exceedance probability substantially increases the upper-bound SLR contribution from basins subject to uncertain future discharge. With σ_b = 0.5μ₁₅, if the upper bound is given by an outcome with a 10% chance of exceedance, non-B15 basins contributes 3–8 cm (up to 50% of the total Antarctic SLR contribution). With a 1% chance of exceedance, the contribution from non-B15 sources is 8–13 cm.

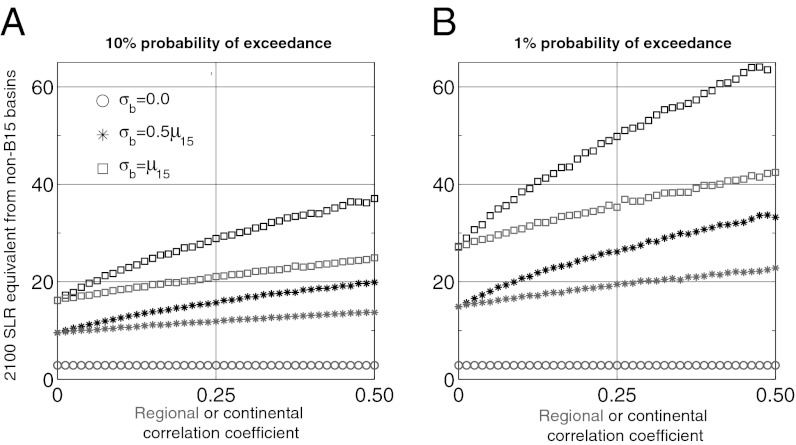
Upper-bound projections may be higher than those shown in Fig. 3 if: (i) discharge growth rates are more uncertain; (ii) discharge growth is strongly and/or widely correlated between drainages; or (iii) a low exceedance probability is specified. In Fig. 4, we examine the non-B15 SLR contribution over a wide range of discharge growth assumptions, using the R08 baseline. Results using the Z11 dataset, the WA set of basins, and alternate growth rate distributions are shown in Figs. S1–S4.

Fig. 4.

Sensitivity to the strength and extent of spatially correlated discharge growth. The upper-bound SLR contribution from all non-B15 basins are shown for three values of discharge growth rate uncertainty (0: circles; 0.5μ_B15: asterisks; μ_B15: squares) at different correlation coefficients (gray: regional, ρ_r; black: continental, ρ_a). In A, the upper bound is defined as SLR with a 10% probability of exceedance; B uses a 1% exceedance probability. The R08 baseline is used.

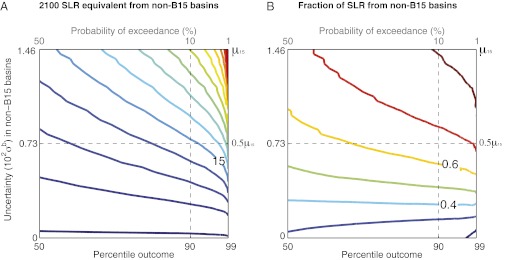
With no uncertainty in non-B15 basin discharge (σ_b = 0.0), the 90th-percentile SLR projection is 2.9 cm higher than the upper bound derived if only B15 is included in projections (circles). This incremental contribution increases by ∼1 cm for each subsequent 0.1% y⁻¹ rise in growth rate uncertainty. As ρ_r increases (gray symbols in Fig. 4), this sensitivity 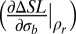is enhanced over all σ_b; other basins are increasingly less likely to provide compensating mass gains. The sensitivity of SLR to changes in σ_b is higher when discharge growth is correlated over the entire ice sheet (black symbols), and is highest at low values of ρ_a. This nonlinear response is more pronounced as the specified exceedance probability is lowered (Fig. 4B).

3. Discussion

Our results demonstrate that the total SLR contribution from Antarctica, as well as the relative importance of non-B15 basins, is sensitive to three key uncertainties: discharge growth trends in B15, observations of mass fluxes at subcontinental scales, and spatial covariance in discharge growth. These physical uncertainties interact with decision-making criteria; the dominant source of uncertainty influencing SLR projections changes depending on the likelihood of the outcome being considered. Median projections are strongly influenced by the observational baseline, unless discharge growth is expected to be high in B15. If non-B15 discharge is uncertain, or outcomes with a lower exceedance probability are required for decision-making, the importance of spatial correlation grows.

3.1. B15 Growth Laws.

Although the quadratic growth law is a better fit for recent B15 discharge (Fig. 3A), and Antarctic mass loss (16) offers evidence that superlinear trends may apply over shorter periods, the physical basis underlying its extrapolation must be considered carefully. Observed decadal changes in B15 convolve long-term retreat (29) and recent stress perturbations due to melting and/or removal from bedrock pinning points (30, 31). Ignoring stabilizing feedbacks that manifest over longer timescales may result in dramatic overestimates of century-timescale SLR.

Recent numerical simulations do not support the maintenance of quadratic increases in ice flux over a century, giving constant or decreasing rates of ice loss following a short (decadal) adjustment period to forcing (24–26, 32, 33,). If the fraction of B15 ice flux discharged through Pine Island Glacier (PIG) remains constant, our linear growth law gives a median PIG SLR contribution comparable to the upper bound of a set of recent numerical simulations (2.7 cm) (24). In contrast, a quadratic law gives a median SLR contribution far greater than numerical simulations (>14 cm).

Although this evidence does not eliminate the possibility of accelerated trends, we judge that a linear growth law (with a large range of uncertainty) better represents current understanding. Reconciling whether the current superlinear growth in Antarctic discharge will be damped over long timescales, and how widespread the underlying processes are (so that these growth trends may be applied, or discounted, in other basins), remains an important area of focus for future observational and modeling efforts.

3.2. Present-Day Mass Balance.

Median projections of SLR may be significantly underestimated if present-day mass imbalances persist. Although the simple continuation in discharge used here lacks a strong physical basis, because ice sheets are far from steady state (8, 17, 20), we suggest that it is more physically justified than an assumption of zero net SLR contribution. However, the optimal choice of observational baseline remains unclear, and projections vary if different subsets of the ice sheet are included in our analysis.

The importance of observational baselines is not limited to extrapolation-based projections; process-based models require validation. The large interregion differences shown here indicate that these datasets are unlikely to be sufficient for model validation at a smaller scale. Furthermore, if 100-y changes in discharge are relatively small or unlikely, the ongoing adjustment to long-term changes in climate is likely to play a large role in 21st-century SLR. Continental-scale models that use only anomalies from a “spin-up” ignore this signal (26). Continued efforts to rationalize (15, 16) and refine (34) observational techniques are necessary.

3.3. Spatially Correlated Discharge Growth.

As shown in Fig. 4, in the presence of uncertainty a widespread, correlated response of many individual glacier systems may generate high SLR upper bounds. Their magnitude depends on the prescribed growth law, the number of uncertain basins, and the form of growth rate distributions (Fig. S1). The nonlinear response to the propagation of discharge growth uncertainty, and its dependence on correlation strength, may be enhanced if heavier-tailed distributions are judged to be more physically appropriate (26, 35).

Fig. 4 indicates that small differences in either correlation strength or spatial extent can influence upper bounds on SLR. Efforts to characterize past or present-day correlations in discharge may thus provide valuable constraints on SLR, particularly if moderate growth scenarios with spatial correlation are deemed more plausible than extreme rates of acceleration in single basins. Present-day observations (16, 34, 36), regional paleo-reconstructions (20, 37), and continental-scale models (12, 38,) may inform these efforts even if they do not provide a comprehensive basis for century-timescale SLR projections.

4. Conclusions

Using a unique framework for assessing the ice sheet contribution to sea level change, we have demonstrated that excluding potential dynamic changes outside basin 15 (B15, drained largely by Pine Island, Thwaites, and Smith glaciers) results in an underestimate of SLR by 2100 over the full range of outcomes needed for decision-making. With linear discharge growth rates and the R08 observational baseline, greater than 20% of Antarctica’s future SLR contribution is derived from non-B15 basins (Fig. 5). Depending on the specified exceedance probability, the non-B15 contribution may be larger than projected 21st-century changes in Antarctic surface mass balance (8). Even with relatively low discharge uncertainty and spatial correlation (σ_b = 0.25μ_B15 and ρ_r = 0.25), roughly half of the 90th-percentile Antarctic SLR (∼18 cm) originates in non-B15 basins. Although the Z11 observational baseline (Figs. S2–S4) gives a smaller non-B15 contribution because of compensating mass gains in East Antarctica, the fractional contribution from non-B15 basins also increases sharply with increasing uncertainty and/or a lower risk tolerance.

Fig. 5.

Sensitivity to the exceedance probability. In A, the upper-bound SLR contribution from all non-B15 basins is plotted as a function of the exceedance probability and discharge growth rate uncertainty. B shows the corresponding fraction of the Antarctic SLR contribution that is derived from non-B15 basins (assuming a linear growth law in B15). The R08 baseline is used; ρ_r = 0.25.

Previous estimates of upper bounds on SLR specify dramatic increases in B15 discharge, with 25- (ref. 3) and 40-cm (ref. 11) SLR equivalent arising from discharge in this basin. Our analysis indicates that a comparable contribution from non-B15 basins requires extremely widespread and uncertain ice discharge growth. However, we suggest that previously published upper bounds may have an implicit exceedance probability that is lower than 1%. At these low probabilities, the contribution of non-B15 basins is large even if uncertainty is relatively small (Fig. 5A); ignoring their possible contribution is inconsistent with the goal of bounding SLR. Furthermore, their exclusion may “anchor” SLR projections (6) and focus uncertainty reductions where their quantitative impact on SLR would be lower.

Because the sensitivity of SLR upper bounds to discharge uncertainty is heightened when discharge growth is spatially correlated or if lower-probability outcomes are explored, our results underscore the importance of a comprehensive assessment of the entire ice sheet that assigns likelihoods to scenarios of ice loss. Without a formal definition, upper bounds are of limited utility, given the strong sensitivity of SLR projections to this assumption and widely varying interpretations of acceptable risks.

5. Outlook

These results are limited by the convolution of external forcing and ice sheet dynamics into discharge growth laws, the aggregation of many physically distinct basins, and the highly abstracted statistical parameters used. However, in this framework, a hierarchy of regional statistical or dynamical models at many spatial scales (13, 39) may be incorporated and updated over time, traceably linking aggregated kinematic approaches with basin-specific, process-based model projections. Where observational data are insufficient or model-based results are less robust, uncertainty estimates may continue to be supplemented by physically based expert judgments (40, 41) (using, for example, bedrock elevation; ref. 42, and/or ocean thermal regimes; refs. 17, 18).

This framework is easily extended to incorporate different future climate and/or emissions scenarios by implementing scenario-dependent discharge (or accumulation) assumptions. Although this may be accomplished using a common relationship, perhaps between ice discharge and global or Southern Ocean temperature projections (19, 26), we suggest that this relationship be carefully examined, given evidence that current (17) and future (18) regional oceanography may be largely uncorrelated with global climate.

A complete accounting of sea level requires the inclusion of Greenland ice sheet dynamics and integration with other terms in the sea level budget (2, 8). Although the Greenland ice sheet is subject to differences in dominant physical processes (16) and may require different mass balance models, this basin-by-basin framework remains applicable. With the inclusion of both present-day ice sheets, probability distributions of local sea level change may be derived by passing mass balance trends to appropriate solid-earth models (43). The statistical linkages between ice sheet drainage basins used in this paper could be extended to all sea level sources driven by common climate forcing (e.g., correlated discharge trends in Greenland and Antarctica, or regional thermosteric and ocean dynamic changes driven by ice discharge; ref. 44).

Local coastal adaptation efforts require projections of sea level that involve physical processes operating over a wide range of timescales (2, 8). Until (and if) these sea level dynamics are captured in a robust, comprehensive, earth system model, this framework provides a viable means to include the contribution of the ice sheets in a more self-consistent, probabilistic manner.

Materials and Methods

Here, we project only the component of global mean sea level change (ΔSL, where positive values indicate SLR) resulting from changes in ice flux (discharge) across Antarctica’s grounding lines. Discharge is assumed to grow at a constant uncertain rate, and these growth rates are sampled from a multivariate normal distribution where α ∼ ₁₈(μ, Σ), using an MC method.

B15 Discharge Growth Rates.

We train square root, linear, and quadratic growth laws on the aggregate historical discharge of B15 (derived from five sets of satellite-derived velocity measurements of Pine Island, Thwaites, Smith, and “interstream” regions between 1974 and 2007) (22) using Eq. 1 with n = 0.5, 1.0, and 2.0. The best fit for each growth law is shown with dashed lines in Fig. 3 (r² values are 0.75, 0.87, and 0.98 for n = 0.5, 1.0, and 2.0). Uncertainty in the fit is then used to inform the future growth rate distribution; for example, the linear trend of 1.46 × 10⁻² y⁻¹ has a 0.79 × 10⁻² y⁻¹ 1σ confidence interval. The growth rate distribution of B15 is then given by a normal distribution with μ₁₅ = 1.46 × 10⁻² y⁻¹ and .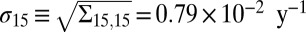

Basin Discharge Growth Rate Covariance Matrices.

If regionally correlated growth is prescribed, basins are aggregated into regions B_r, where r = 1, 2, 3, 4, 5; each region contains the set of basins B = {b₁, b₂,…,b_n} (Table 1). Σ is given by a block-diagonal matrix where the blocks (regions) have a within-region correlation and no cross-region correlation:

The regional correlation coefficient (ρ_r) is equal to 1 if i = j. If growth rates are correlated across the continent,

and i = j = 1, 2,…,18. The continental correlation coefficient (ρ_a) is equal to 1 if i = j.

Each MC simulation involves a specification of the SD of the growth rate in non-B15 basins (0 ≤ σ_b ≤ 1.46 × 10⁻² y⁻¹), and either ρ_a or ρ_r. Here, σ_b and ρ_r are assumed to be the same for all five regions; future analyses may treat them independently. Growth rates used in representative basins for three different simulations (each with a 90th-percentile SLR outcome of ∼20 cm) are shown in Fig. S5.

Mass Balance Model, Sampling, and Aggregation.

Each MC simulation contains 40,000 realizations (k) that use a unique growth rate 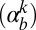for each basin. The net mass balance of a basin is given by

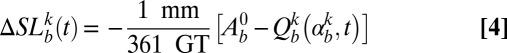where accumulation, A⁰ (in GT y⁻¹), is constant, and discharge increases at a constant linear rate. In B15, discharge is given by

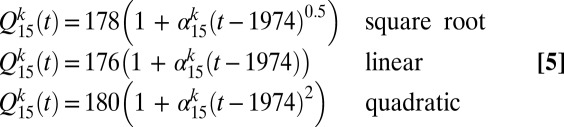Only a linear extrapolation is used for the Z11 analyses, and Q¹⁹⁷⁴ = 163 GT y⁻¹. This assumes that the adjustments to R08 discharge applied in Z11 are constant in time.

For all other basins, the discharge is given by

Discharge in the R08 and Z11 analyses is assumed to represent year 2000 discharge, Q²⁰⁰⁰ (Table 1). Q²⁰⁰⁰ and A²⁰⁰⁰ are always taken from the same analysis.

For each realization, the cumulative sea level contribution of each basin is aggregated by region,

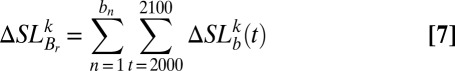The aggregate sea level change over all regions across all realizations provides a cumulative distribution function for SLR.