An Efficient Dynamic Programming Algorithm for Phosphorylation Site Assignment of Large-Scale Mass Spectrometry Data

Abstract

Phosphorylation site assignment of large-scale data from high throughput tandem mass spectrometry (LC-MS/MS) data is an important aspect of phosphoproteomics. Correct assignment of phosphorylated residue(s) is important for functional interpretation of the data within a biological context. Common search algorithms (Sequest etc.) for mass spectrometry data are not designed for accurate site assignment; thus, additional algorithms are needed. In this paper, we propose a linear-time and linear-space dynamic programming strategy for phosphorylation site assignment. The algorithm, referred to as PhosSA, optimizes the objective function defined as the summation of peak intensities that are associated with theoretical phosphopeptide fragmentation ions. Quality control is achieved through the use of a post-processing criteria whose value is indicative of the signal-to-noise (S/N) properties and redundancy of the fragmentation spectra. The algorithm is tested using experimentally generated data sets of peptides with known phosphorylation sites while varying the fragmentation strategy (CID or HCD) and molar amounts of the peptides. The algorithm is also compatible with various peptide labeling strategies including SILAC and iTRAQ. PhosSA is shown to achieve > 99% accuracy with a high degree of sensitivity. The algorithm is extremely fast and scalable (able to process up to 0.5 million peptides in an hour). The implemented algorithm is freely available at http://helixweb.nih.gov/ESBL/PhosSA/ for academic purposes.

I. Introduction

Mass spectrometry is a fundamental part of any modern proteomics research platform for large-scale protein identification and quantification [1]. In a typical liquid chromatography-coupled tandem mass spectrometry (LC-MS/MS) proteomic experiment, ionized peptides are introduced into a mass spectrometer at the ion source in the form of aqueous solutions, then desolvated and transferred into the gas phase as ions. Various fragmentation strategies such as CID (Collision Induced Dissociation) and HCD (Higher Energy Collisional Dissociation) are used to get peptide sequence information. These two fragmentation methods tend to generate ostensibly similar spectra for the same peptide, but with slight differences in the presence and relative abundance of certain ions. Typically, search algorithms are used to match the fragmentation spectra to sequences in online databases in order to identify the peptides in the mixture [3], [4].

Mass spectrometry based large-scale phosphoproteomics has been shown to have useful applications in biology such as studying the regulation of cellular processes [5], cancer molecular therapeutics [6] and many others [7]–[10]. With the advent of efficient mass spectrometers, computational tools are essential that can deal efficiently with large data sets. There are many computational obstacles that are currently faced in post-acquisition analysis of phosphoproteomic data such as phosphopeptide filtering [11], false discovery rate estimation [12], quantification of peptides and proteins from large datasets [10], and accurate clustering of large-scale mass spectrometry data [34].

Traditionally, identifying the phosphorylation site(s) within a phosphopeptide has been done by manual validation of the spectra. However, with the advent of high throughput mass spectrometers, the data sets generated are generally vast and manual site assignment is no longer practical. Accurate site assignment is critical for large-scale phosphoproteomics studies, which typically seek to identify the protein kinase classes that are regulated in a particular experiment by identifying the patterns of amino acids up- or downstream from the phosphorylation site that are over-represented in a data set, as discussed by [14]. Systematic errors in site assignment would undermine these calculations and the conclusions that arise from them. Therefore, there is a need for an accurate, freely available site-assignment algorithm that can deal with various kinds of data sets and can make computations in a reasonable amount of time.

The main goal of this study was to design and test a dynamic programming strategy for phosphorylation site assignment. Our algorithm maximizes the objective function that is based on the sum of the peak intensities that match to the theoretical peptide spectrum. The algorithm is differentially optimized for CID and HCD fragmentation characteristics using multiple data sets. After optimizing the objective function, each peptide configuration is scored. A quality post-processing is then introduced that exploits the specific characteristics of the mass spectrometry data to stratify the assigned sites based on the scoring function and associated parameters. The algorithm is able to correctly assign phosphorylation sites with > 99% accuracy¹ with a high degree of sensitivity for experimentally generated data sets of peptides with known phosphorylation sites. Dynamic programming allows us to devise a linear time and space strategy making it a highly efficient system that can accomplish site assignments for large data sets within minutes.

A. Problem Statement and Background Information

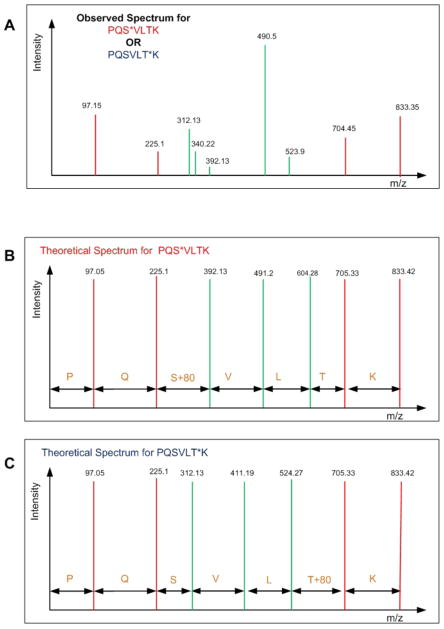
Let there be a fragmentation spectrum S = (m₁, i₁), (m₂, i₂), · · ·, (m_Q, i_Q) that is extracted from the mass spectrometry data where m_x represents the m/z ratio of the peptide fragment and i_x represents the intensity of the peptide at position x where 0 < x ≤ Q, where Q is the total number of peptide fragments. Typically, a standard peptide identification algorithm (e.g. Sequest and Mascot) performs well in matching a spectrum to a correct peptide sequence. In the case of phosphopeptide identification, however, those algorithms still have limited capability in assigning a correct phosphorylation site in the top candidate peptide sequence due to the similarity between the spectra of all potential configurations of that phosphopeptide (i.e. a difference in the position of the phosphorylated residue(s)) [15], [16]. Among all of the peaks in a fragmentation spectrum, there are only certain ones that can help differentiate between possible phosphopeptide configurations. Those peaks are called phosphorylation site-determining peaks. Our objective is to decide which of the peptide configurations has site-determining peaks that correspond best to the observed spectrum. Fig. 1 shows an observed spectrum and two theoretical spectra of two possible phosphopeptide configurations. The problem is to decide which phosphopeptide configuration is the correct one for the given observed spectrum. The green peaks in Fig. 1 represent site determining peaks for the two peptides and the red peaks represent non-site determining peaks. By generating the theoretical spectra for both of the peptides, the following problems can be observed. Almost none of the peaks match exactly with the peaks that are generated theoretically. Furthermore, there are additional peaks that are observed in the spectrum but are not present in the theoretical spectra (e.g peaks at 340.22). Lastly, it can be observed that some peaks are close to the theoretical peak but have amplitudes that are very close to the noise level and there is no way to know if these peaks are actual peaks or just noise (e.g. peak at 392.13). All of these problems are frequently observed in real spectra making the assignment of phosphorylation site a difficult computational problem.

Fig. 1.

Simplified problem statement: Observed spectrum of a mono-phosphorylated peptide (PQSVLTK) is shown (A) and the problem is to determine which of the possible configurations PQS*VLTK (shown in B) or PQSVLT*K (shown in C) (* indicates phosphorylated residue) has the theoretical spectrum that corresponds best to the observed spectrum.

There have been a number of algorithms that automate the process of phosphorylation site assignment for mass spectrometry data [13], [15], [17]–[21]. Among them is Ascore [15], a well known algorithm that uses probabilistic analysis for phosphorylation site determination. Another commonly used algorithm is PhosphoScore [13] that uses a graph theoretic approach combined with Gibbs sampling to determine the phosphorylation sites.

II. METHODS

A. Algorithm: PhosSA

In this section we present the details of our dynamic programming algorithm. We present the mathematical formulation, introduce the quality post-processing, and also analyze the time and space complexities of PhosSA.

PhosSA takes the search results from Sequest [4] as input and is theoretically extendible to accept the output of other search algorithms [3], [22]. The search results from Sequest report multiple phosphopeptide configurations for each spectrum. PhosSA establishes theoretical site determining peaks based on the configurations reported by Sequest and m/z ratios of those peaks are calculated. The observed spectrum is then compared to each set of theoretical site determining ions for each phosphopeptide configuration, taking into consideration possible neutral loss peaks and different charge states which add markedly to the complexity of the optimization task. The intensities of observed peaks that only match theoretical site-determining peaks (within a define m/z threshold) of each phosphopeptide configuration are summed up to a Φ score. The phosphopeptide configuration that has the highest Φ score for each spectrum is selected using dynamic programming as described in section II-B. After the optimization, a quality post-processing is introduced that allows poor quality assignments to be eliminated. An outline of the algorithm is shown in Algorithm 1 and Fig. 2. The algorithm has been implemented in Java(TM) SE Runtime Environment (build1.6.0). The experiments were conducted on a Dell server consisting of 2 Intel Xeon(R) Processors, each running 2.40 GHz, with 12000 KB cache and 64GB DRAM memory. The operating system on the server is Linux RedHat enterprize version with kernel 2.6.9-89.ELlargesmip.

Algorithm 1.

PhosSA

Require: Peptide search results from Sequest containing lists of possible phosphopeptide configurations and the corresponding spectral data (m/z and peak intensities):

Ensure: The correct phosphorylation site assignment: Read the Sequest search results with the corresponding spectral data Extract theoretical site determining peaks based on the configurations reported by Sequest and calculate m/z ratios of those peaks. Compare observed spectrum to each set of theoretical site determining peak for each phosphopeptide configuration. Calculate the optimal Φ score for each phosphopeptide configuration using dynamic programming. Select the phosphopeptide configuration that has the highest Φ score for each spectrum as an input for the quality post-processing. Classify the peptides as passed or ambiguous using the proposed quality post-processing criteria Output the phosphopeptide data that exceed quality threshold based on the quality post-processing.

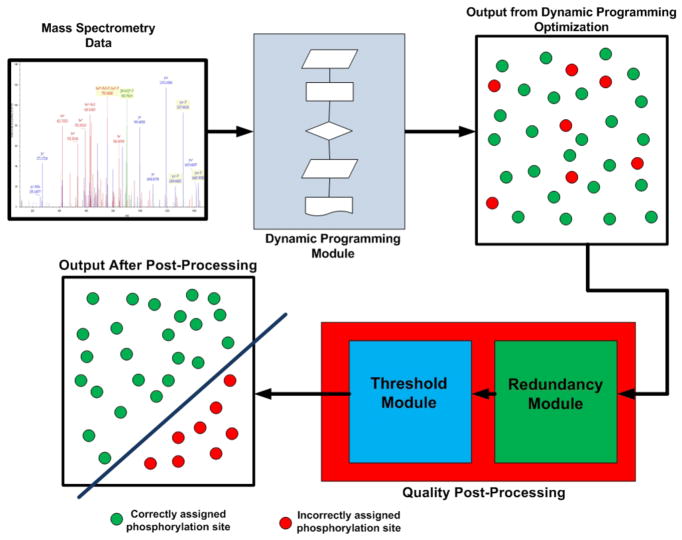
Fig. 2.

Flow diagram for PhosSA algorithm. Mass spectrometry data are fed into the dynamic programming module. The dynamic programming module output is the optimal assignment for each peptide, regardless of the overall quality of match. To sort the assignments by quality of match, a quality post-processing is used. The quality post-processing uses two additional criteria (Threshold (dC_n) and redundancy) that allow discrimination between phosphorylation site assignments that are correctly vs. incorrectly assigned.

B. Dynamic Programming Based Phosphorylation Site Assignment Algorithm

In this section we mathematically formulate the problem, define the criteria used to evaluate the correct phosphorylation site(s), and present a dynamic programming algorithm for finding the optimal solution.

1) Mathematical Formulation

We will consider an instance of the assignment of a phosphopeptide of length L identified from a spectrum. Let the index of any amino acid in the peptide be represented by i where 1 ≤ i ≤ L. Now let the mass-to-charge (m/z) ratio of the amino acid at position i be represented as M(i) and m/z of the b-ion be represented as Mb(i) up to i. Similarly, m/z of the y-ion can be represented as My(i) up to i. Then the sub-problem of calculating the theoretical m/z of the b-ion can be formulated as:

$$Mb(i)=Mb(i-1)+M(i)$$ (1)

Also, the y-ion can be calculated in terms of b-ion m/z values

$$My(i)=Mb(L)-Mb(L-i)$$ (2)

Let the intensity of the peak observed for theoretical mass M be I[M]. Then for our purposes the maximum peak that is selected for mass M is

$$I{[M]}_{\mathit{max}}=\mathit{max}(I[q])$$ (3)

where the maximum peak intensity window searched is (M − δ/2) ≤ q ≤ (M + δ/2) and δ is chosen based on the mass accuracy of the instrument.

Now let the objective function Φ(L) that has to be optimized (maximized) for a single peptide of length L be

$$\mathrm{\Phi }(L)=\sum _{u=1}^{L}I{[Mb(u)]}_{\mathit{max}}+\sum _{r=1}^{L}I{[My(r)]}_{\mathit{max}}$$ (4)

The rationale is that the intensity of the peaks in the spectrum provides an appropriate weighting for the matched peaks. The same objective function can be formulated with a similar argument for smaller fragmentation ions such as neutral losses of phosphoric acid P_h, H₂O and NH₃. Let a set S be defined as S = {b, b – H₂O, b – NH₃, b – P_h, b– P_h – H₂O, b – P_h – NH₃, y, y – H₂O, y – NH₃, y – P_h, y – P_h – H₂O, y – P_h – NH₃}; where S corresponds to all possible fragmentation ions. Here the notation b – X (X corresponds to H₂O, NH₃ and phosphoric acid P_h) is used to indicate the m/z of a b-ion minus the m/z corresponding to neutral loss of H₂O (18/z), NH₃ (17/z), or phosphoric acid (98/z). The y-ions are similarly defined. The need to identify and match the neutral loss peaks substantially complicates the optimization problem. A naive implementation of the above score (Equation 4) for each peptide would make the asymptotic time equal to O(L^|S|×charge) for each peptide, where charge is the charge state on the peptide and |S| is the number of elements in the set. For the above set S, the asymptotic times then approach O(L^12×charge). For a +3 charge state of the peptide, the number of ions would approach O(L³⁶) for a single peptide. For N peptides the running time would be asymptotic to O(NL^|S|×charge) ≈ O(NL³⁶). This is not a practical approach even for a small number of peptides. However, the problem can be formulated more efficiently using dynamic programming with linear running time using the subproblems from fragmentation ions (Set S), a strategy that can succeed with large data sets².

Dynamic programming

We apply the standard dynamic programming approach as formulated for many problems in [23]. Finding the optimal solution for the peptide of length L for {1, 2, · · ·, L} involves looking at the optimal solutions of smaller sub-problems of the form {1, 2, · · ·, j} where j < L. Thus, for any value j from 1 and L − 1, let O_(j) denote the optimal solution of the problem for peptides size from {1, · · ·, j} and let Φ(j) denote the value of this solution. The optimal solution that we are seeking is Φ(L). For optimal solution O_(j) on {1, 2, · · ·, j} either j ∈ O_(j) (index j belongs to the optimal solution) in which case

$$\mathrm{\Phi }(j)=I{[M[j]]}_{\mathit{max}}+\mathrm{\Phi }(j-1)$$ (5)

or j ∉ O_(j) (j does not belong to the optimal solution) in which case O_(j) = O_(j−1) and therefore Φ(j) = Φ(j − 1). Since, there are only two possibilities, we can further say:

$$\mathrm{\Phi }(j)=\mathit{max}(I{[M[j]]}_{\mathit{max}}+\mathrm{\Phi }(j-1),\mathrm{\Phi }(j-1))$$ (6)

The solution O_(j) belongs to the optimal solution if and only if:

$$I{[M[j]]}_{\mathit{max}}+\mathrm{\Phi }(j-1)\ge \mathrm{\Phi }(j-1)$$ (7)

and

$$I{[M[j]]}_{\mathit{max}}\ge \zeta$$ (8)

where ζ is equal to the threshold of smallest peak intensity considered and depends on the kind of fragmentation ion³. An instance of the algorithm is shown in Fig. 3.

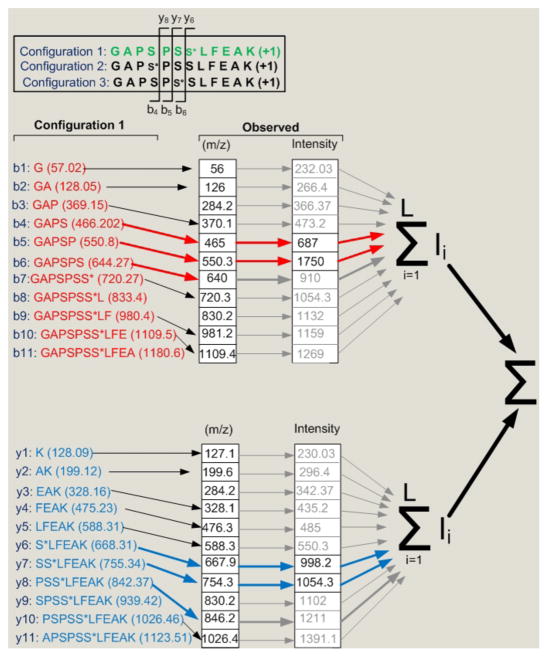
Fig. 3.

A diagram showing the concept behind the dynamic programming algorithm. Out of three candidate configurations, the site determining ions i.e. those fragment ions that would be specific for a particular phosphopeptide configuration, were established (b₄ to b₆ and y₆ to y₈, shown in top panel). The theoretical m/z of configuration 1 are shown. The observed m/z that only match (within a specified mass tolerance) to the theoretical site determining ions are then selected (indicated by red and blue arrows). The intensities of these site determining ions are then summed for each phosphopeptide configuration considered. Note that this diagram oversimplifies the problem because it ignores multiple charge states and neutral losses as discussed in text.

Additional algorithmic constraints

The additional algorithmic constraints are required because of the possibility of two or more fragmentation ions having the same m/z.

We consider coincidence of two fragment ions with the same m/z here; however, the argument is easily extendible to more than two fragment ions. The constraints added are as follows: If neither of the fragmentation ions is site determining, they are not considered. If one of the fragmentation ions is a site determining ion and the other is not, they are still not considered by the algorithm. The rationale behind this is that if there is one ion that is site determining and the other is not, there is no way to know which ion is correctly assigned to that peak. If, however, both of the fragmentations ions are site determining, predicting the same phosphorylation configuration, we consider the peak intensity measured to be made up of both fragmentation ions.

2) Quality post-processing

Following dynamic programming analysis, the data consist of phosphorylation site assignments that can be made with varying levels of confidence. This lead us to formulate post-processing steps to filter the data and eliminate the lower confidence assignments. To address this challenge, we incorporated two steps, namely threshold and redundancy analysis.

Threshold criterion

For this algorithm, threshold is similar to the deltaC_n (dC_n) function used in algorithms like Sequest [3], [4], [24], [25]. The dC_n threshold defined in our case is:

$${dC}_n=\frac{\mathrm{\Phi }{(L)}_{\mathit{Highest}}-\mathrm{\Phi }{(L)}_{\mathit{SecondHighest}}}{\mathrm{\Phi }{(L)}_{\mathit{Highest}}}$$ (9)

The rationale behind the threshold is that if the dC_n value is high, then the top scoring assignment is more likely to be correct. If there are two scores very close to each other, then it is very difficult to decide if the peptide that has the highest score is correct. However, based on a preliminary test on a set of known phosphopeptides, only 22% of our data contained high enough dC_n values (> 0.9) to confidently assign the correct site with 95% accuracy. Using just the threshold (dC_n) criterion would eliminate spectra just because the second best score was very close to the best score. Therefore, we devised an additional criterion that would take into account situations like this in which we have high degree of redundancy.

Redundancy criterion

During mass spectrometry it is common for abundant peptides to get selected for fragmentation multiple times [26]–[28]. Hence, it is a natural step to exploit this additional redundancy information for the quality post-processing. If the same peptide is identified multiple times with the same site of phosphorylation, then regardless of the dC_n for individual spectra, the phosphorylation site determined has a higher chance of being correct.

Using a simple probabilistic analysis, the same peptide assigned the same phosphorylation site at least 7 times can be shown to give an accuracy of 99% or higher. As a proof of concept, we analyzed a phosphopeptide library in order to determine the phosphopeptide assignment accuracy using only the redundancy post-processing. The accuracy was increased in accordance with the increasing redundancy metric (number of times that a peptide configuration is assigned by the dynamic programming algorithm) and reached 100% when the redundancy metric was 4 or more. For our calculations, we conservatively set the post-processing criteria as follows: if a phosphopeptide configuration has a redundancy of 7 or more, we let this configuration pass without considering dC_n. If the redundancy metric is less than 7, a phosphopeptide needs to have dC_n more than 0.99 in order to pass the quality post-processing.

C. Analysis of Computational and Memory Complexity

The running time of the program depends on the theoretical complexity of the implemented algorithm. The time complexity of the algorithm is a theoretical metric that defines the running time of the algorithm as a function of the size of the input data set. The time complexity of the algorithm can be broken down into two components. The dynamic programming part of the algorithm will run in O(L) time, where L represents the average length of the peptides. Since there are N peptides the total time complexity would be equal to O(NL). The second part of the complexity is for the post-processing calculations. The dC_n threshold calculation is done during the initial dynamic programming phase of the algorithm and can be accomplished in constant time O(c). The number of compute cycles required for redundancy metric calculation is variable and depends on the redundancy in the data. Assuming that there is sufficient redundancy in the data, the average running time is O(kN) where k is the number of times a peptide appears with same phosphorylation site. Therefore the time complexity of PhosSA is equal to T = O(NL + c + kN) ≈ O((k + L)N). This means that the running time should be linear with the number of peptides. The memory complexity can also be calculated to be equal to O(NL) with a similar argument.

D. Sample Preparation and Mass Spectrometry Analysis

PhosSA accuracy and sensitivity were tested using data sets from mass spectrometry analysis of synthesized phosphopeptides for which the phosphorylation sites were known. The algorithm was tested on data obtained by mass spectrometry with a number of variables: 1) different fragmentation methodologies (HCD vs CID), 2) varying peptide amounts, 3) total number of phosphorylation sites, and 4) the position of the phosphorylation sites within the peptide. These experiments allowed us to simulate a variety of experimental conditions encountered in “real world” samples.

The experiments were conducted in accordance with an animal protocol approved by the Animal Care and Use Committee of National Heart Lung and Blood Institute (NHLBI), NIH ACUC protocol No. H-0110. A piece of freshly isolated rat liver was minced and sonicated in guanidine-HC1(6M,3ml). The samples were then spun at 16000 × g to pellet the cellular debris and cleared liver lysate was reduced and alkylated [1]. A peptide standard corresponding to the C-terminal sequence of the water channel Aquaporin-2 (AQP2) from rat, (Biotin-LC-CEPDTDWEEREVRRRQS*VELHS*PQSLPRGSKA) phosphorylated at both S256 and S261 were added to 500 μg aliquots of liver sample (prior to trypinization) with distinct amounts of 0.2 nmol, 20 pmol and 2 pmol and were named AQP2-H-(S256/S261), AQP2-M-(S256/S261), AQP2-L-(S256/S261) respectively. The same procedure as above was repeated for another AQP2 peptide standard (Biotin-LC-CEPDTDWEEREVRRRQSVELHSPQS*LPRGSKA) phosphorylated at S264, with amounts of 0.2 nmol, 20 pmol and 2 pmol and were named AQP2-H-(S264), AQP2-M-(S264), AQP2-L-(S264) respectively. Peptide samples were desalted on a 1 ml HLB cartridge and phosphopeptides were enriched via IMAC, Pierce Phosphopeptide Isolation Kit. Samples were then desalted using C₁₈ Ziptips (Millipore) and then were dissolved in 0.1% formic acid prior to analysis by mass spectrometry.

The samples were then analyzed on an Agilent 1100 nanoflow system LC (Agilent Technologies) connected to a Orbitrap LTQ Velos mass spectrometer (Thermo Scientific, San Jose, CA). Samples were run using optimized parameters with collision-induced dissociation (CID) at 35% normalized collision energy as well as higher energy collisional dissociation (HCD) at 45% normalized collision energy. MS spectra were analyzed using Proteome Discoverer version 1.2 software running the Sequest search algorithm. Spectra were searched against a Rat Refseq database with the following parameters for CID as well as HCD samples: Max. missed cleavage = 3, precursor mass tolerance = 25 ppm, fragment mass tolerance = 0.05 Da, static modification: carbamidomethyl (C: +57.021 Da), dynamic modifications: Phospho (S,T,Y: +79.966), Deamidation (N,Q: +0.984), Oxidation (M: +15.995). Each of the samples were run separately with CID as well as HCD fragmentation.

III. RESULTS

The performance evaluation of the algorithm is divided into four parts. The first three parts deal with assessing the accuracy and sensitivity of PhosSA using data sets from actual mass spectrometry analysis of peptides with known phosphorylation sites. The objectives of this quality analysis were to determine: 1) performance characteristics of PhosSA with HCD vs. CID samples, and the effect of different amounts of the sample on the quality of the site assignment, 2) performance exhibited by PhosSA when compared to other site assignment algorithms, 3) quality of the assignment with variable site determining peaks (i.e. with increasing difficulty of the site assignment). The fourth part of this section deals with a traditional computational performance metric (i.e. execution time). For the following experiments, Sequest results are taken as input with 1% FDR and top 10 peptides reported for each scan.

A. Assessing the Sensitivity and Accuracy using PhosSA for HCD and CID Data Sets and the Effect of Different Amounts of Phosphopeptide Standards

These data sets consisted of data from LC-MS/MS analysis of 6 samples (each run separately with CID and HCD) as discussed in Methods section (results from PhosSA shown in Table I). The two fragmentation methods generate primarily b-type and y-type ion spectra, but are predicted to have differences in the presence and relative abundance of multiple types of neutral loss ions. To our knowledge, site assignment accuracy and sensitivity have not been compared between these two fragmentation methods using any phosphorylation site assignment algorithm.

TABLE I.

Summary of PhosSA and Sequest site assignment results for AQP2 mass spectrometry data set using CID and HCD fragmentations (see text for description). DNP denotes did not pass post-processing criteria

CID data sets	PhosSA sensitivity(%)	PhosSA accuracy (%)	Sequest accuracy (%)
AQP2-H-(S256/S261)	91.6	100	94.6
AQP2-M-(S256/S261)	90.7	100	94.4
AQP2-L-(S256/S261)	0	DNP	100
AQP2-H-(S264)	91.5	100	100
AQP2-M-(S264)	50	100	88.8
AQP2-L-(S264)	0	DNP	60
HCD data sets
AQP2-H-(S256/S261)	92.2	100	94.5
AQP2-M-(S256/S261)	93.3	100	96
AQP2-L-(S256/S261)	64.3	100	100
AQP2-H-(S264)	97.7	100	74.2
AQP2-M-(S264)	93.1	100	72.4
AQP2-L-(S264)	0	DNP	50

We analyzed these data sets with PhosSA using a high value for the quality post-processing threshold (dCn = 0.99) and obtained the results shown in Table I. For CID, PhosSA sensitivity is greatest (> 90%) for samples that have the highest amounts. For HCD, the sensitivity is higher than the CID samples over all peptide amounts. For HCD samples with medium and high amounts, the sensitivity is higher than 90%. For samples with low peptide amount, both CID and HCD [AQP2-L-(S256/S261) and AQP2-L-(S264)], the sensitivity drops. The accuracy of PhosSA for all data sets that passed the post-processing criterion was always observed to be 100%. The accuracy of the site assignment for the top candidate peptide using Sequest is lower than obtained with PhosSA as shown in Table I.

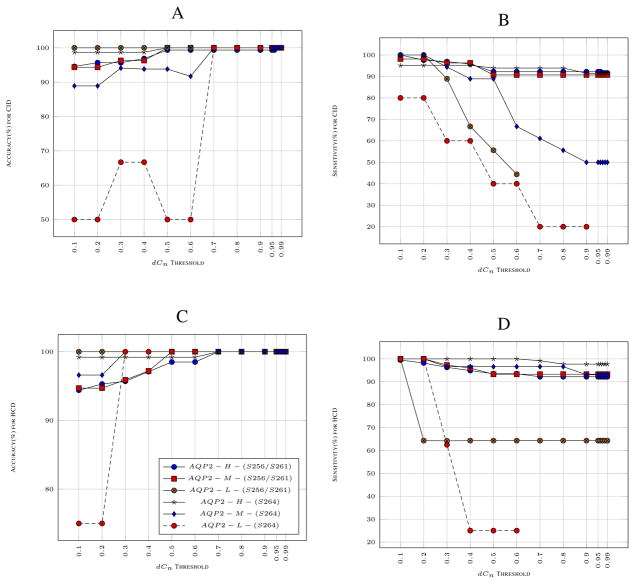
As explained in Methods, the PhosSA post-processing utilizes two criteria: dC_n threshold and redundancy. Although the redundancy threshold remains a constant (7 spectra all showing the same assignment) in our algorithm, dC_n threshold can be adjusted by the user. Intuitively, the lower the dC_n threshold, the greater the number of peptides that would pass at the expense of accuracy. The optimal dC_n threshold that maximizes sensitivity and accuracy is likely to be dependent on the properties of the data. For our experiments, we varied the threshold from 0.10 to 0.99 and recorded the accuracy and sensitivity for both CID and HCD data shown in Fig. 4. With reasonable dC_n threshold values (0.70 – 0.99), the accuracy remains very close to 100% for all data sets and the sensitivity is greater than 90% for most of the data sets with medium and high peptide amounts. The most variable changes in sensitivity can be observed for low peptide amount samples. In summary, site assignment using PhosSA appears to be more reliable with HCD data than with CID data.

Fig. 4.

Sensitivity and Accuracy for the 6 samples are shown with varying (dC_n) threshold: A shows the accuracy and B shows the sensitivity for CID samples. C shows the accuracy and D shows the sensitivity for HCD samples. AQP2-H-(S256/S261), AQP2-M-(S256/S261) and AQP2-L-(S256/S261) consists of phosphopeptide standard (Biotin-LC-CEPDTDWEEREVRRRQS*VELHS*PQSLPRGSKA) phosphorylated at both S256 and S261 in distinct amounts of 0.2 nmol, 20 pmol and 2 pmol respectively. AQP2-H-(S264), AQP2-M-(S264) and AQP2-L-(S264) consists of peptide standard (Biotin-LC-CEPDTDWEEREVRRRQSVELHSPQS*LPRGSKA) phosphorylated at S264 in amounts of 0.2 nmol, 20 pmol and 2 pmol respectively.

B. Comparison to Other Phosphorylation Site Assignment Algorithms

In this study, we compare PhosSA with Ascore [15] and PhosphoScore [13]. The first data set consisted of spectra from two distinct, doubly-phosphorylated aquaporin-2(AQP2) phosphopeptides, AQP2 peptides phosphorylated at S256/S261 called AQP2-H-(S256/S261) and AQP2 peptides phosphorylated at S256/S269 called AQP2-H-(S256/S269), separately spiked into liver cell lysates, a tissue that does not express AQP2 endogenously [13]. PhosSA surpassed both of these tools in both sensitivity and accuracy as shown in Table II (using recommended thresholds of 19 for Ascore and 1% D-score for PhosphoScore).

TABLE II.

Summary of results of phosphorylation site assignment using mass spectra obtained from the analysis of AQP2 peptides.

	AQP2-H-(S256/S261) and AQP2-H-(S256/S269)
Algorithm	Sensitivity(%)	Accuracy(%)
AScore	52.4	98.1
Phosphoscore	63.9	92.2
PhosSA	90.9	100.0

To test whether PhosSA can deal with a variety of a phosphorylated peptides, we tested our algorithm on a second data set (provided by Steven Gygi) [13], [15] which is derived from mass spectrometry analysis of a library consisting of 380 phosphopeptides (out of which 162 are distinct peptides) from three different families i.e. AS*PXPXAXFEA, GAPX-PXS*XFEA and ADZZS*STZZFEAK where X is one of the amino acids ADEFGLSTVY and Z is one of the amino acids SDLFGHP. For this data set, PhosSA performed comparable to PhosphoScore in sensitivity and to Ascore in accuracy, combining the best features of the two algorithms (Table III). Our experiments show that using PhosSA with varying dC_n for the phosphopeptide library, the sensitivity did not drop below 70% and with very low thresholds the accuracy was always observed to be greater than 85% (results not shown).

TABLE III.

Summary of results for phosphorylation site assignments using mass spectra obtained from the analysis of Phosphopeptide Library (Ascore > 19, 1% D-score PhosphoScore).

	Phosphopeptide Library
Algorithm	Sensitivity(%)	Accuracy(%)
AScore	32.1	99.0
Phosphoscore	76.3	96.6
PhosSA	70.3	98.6

C. Assessing the Accuracy and Sensitivity using a Phosphopeptide Libary

Here we analyze the sensitivity and accuracy of the mixed phosphopeptide dataset, described in the previous paragraph, from LC-MS/MS analysis with respect to the individual peptide families with known phosphorylation sites. The families differed based on the distance between the actual phosphorylated residue and neighboring potentially phosphorylatable residues. As the distance between neighboring residues decreases, the number of potential site-determining ions also decreases, making it more difficult to correctly assign the phosphorylation site. The families are listed in the order of increasing difficultly: AS*PXPXAXFEA, GAPXPXS*XFEA and ADZZS*STZZFEAK where X is one of the amino acids ADEFGLSTVY and Z is one of the amino acids SDLFGHP. Our experiments indicate that PhosSA exhibited a high degree of accuracy and sensitivity for all three families. Even for the most difficult data set that has serines/threonines in consecutive order (Family 3), PhosSA is able to predict sites with 100% accuracy with a high degree of sensitivity. This is in large part due to the inclusion of the redundancy criterion (results not shown). These results show that PhosSA is capable of accurate site assignments with various configurations of phosphopeptides making it a highly versatile tool for large-scale data sets.

D. Execution Time

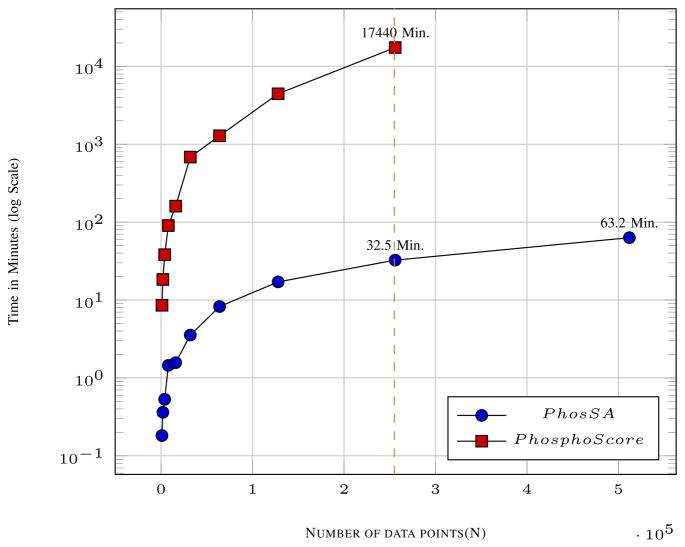
The complexity analysis for PhosSA suggests that the running time should be linear with the number of peptides (see Methods). Although the designed algorithm gives theoretical guarantees on time complexity, it is important to experimentally determine running times. Large data sets are required to test the execution time and scalability of the algorithm. In Fig. 5, we report results for up to 0.5 million peptides from replicated HCD data sets using our algorithm. This task was accomplished by PhosSA in 63.2 minutes using a compute server with modest performance characteristics (see Methods) whereas Phosphoscore was substantially slower. We conclude that because of its speed (time increases linearly with increasing peptides), PhosSA can readily process data sets that typically result from state-of-the-art phosphoproteomics analysis. The code for Ascore is not available for us to assess the running time of the algorithm.

Fig. 5.

Execution times with increasing number of spectra. The time taken by PhosSA for 2.5 × 10⁵ spectra is just 32.5 minutes whereas for PhosphoScore it takes 17740 minutes.

IV. Discussion

We have described a dynamic programming-based phosphorylation site assignment algorithm for mass spectrometry data. To our knowledge, this is the first report of a dynamic programming solution to the site assignment problem. The dynamic programming framework allowed us to devise a highly accurate algorithm capable of dealing with large data sets. A detailed algorithmic technique was described and time and space complexity analysis was presented. PhosSA assigns a single score to each phosphopeptide with single or multiple phosphorylation site(s), followed by post-processing criterion. A rigorous quality assessment of the results from PhosSA was done using data from experimental mass spectrometry of peptides with known phosphorylation sites with varying characteristics such as the position of the sites, the peptide amounts in the samples and CID/HCD fragmentation methodologies. For all of the experiments that we conducted, PhosSA carried out site assignment tasks rapidly (0.5 million peptides per hour) with a high degree of accuracy (close to 100%) and sensitivity (close to 90%). PhosSA was also able to correctly identify sites for phosphopeptides that are most difficult to assign due to the presence of consecutive phosphorylatable residues (Family 3). The proposed algorithm was also compared with other well-established site assignment tools, namely Ascore and Phosphoscore. Using a variety of test data sets, PhosSA was able to give better accuracy with a much higher degree of sensitivity when compared to either of these tools. The proposed algorithm is able to successfully assign sites for CID data sets. Unlike Ascore and Phosphoscore, the proposed algorithm is also able to deal with HCD data sets. It is also capable of using data from iTRAQ- or SILAC-labeling experiments as input [30]. The techniques introduced in this manuscript suggest new areas of exploration that can be pursued: 1) The algorithm is currently compatible with standard Sequest (.dta and .out) search results as well as the new Proteome Discoverer format (.msf). It would be useful to expand the capability of the algorithm to allow as input search results from other algorithms such as Mascot and OMSSA. 2) The algorithm has been tested on experimental data from a number of peptides with known phosphorylation sites with different characteristics. However, producing these biological samples is costly and sometimes not possible. One solution to this problem is a simulator that could simulate mass spectrometry data in an accurate manner [31], [32]. Simulators have been used successfully in other domains of computational biology such as creating and analyzing multiple sequence alignments & phylogenetic trees and for producing next generation sequencing reads. The simulator could produce synthetic data with “ground truth” that would make the quality assessment for such algorithms systematic. It could lead to benchmarking for different research problems in proteomics. 3) Currently, our algorithm is optimized for phosphoproteomic data. However, it could readily be adapted for analysis of other post-translational modifications. We are also working on high performance algorithms for site assignment and a preliminary report on parallel algorithm using multicore systems for mass spectrometry data can be found at Saeed et. al. [33].