Shrinkage Estimators for a Composite Measure of Quality Conceptualized as a Formative Construct

Abstract

Objective

To demonstrate the value of shrinkage estimators when calculating a composite quality measure as the weighted average of a set of individual quality indicators.

Data Sources

Rates of 28 quality indicators (QIs) calculated from the minimum dataset from residents of 112 Veterans Health Administration nursing homes in fiscal years 2005–2008.

Study Design

We compared composite scores calculated from the 28 QIs using both observed rates and shrunken rates derived from a Bayesian multivariate normal-binomial model.

Principal Findings

Shrunken-rate composite scores, because they take into account unreliability of estimates from small samples and the correlation among QIs, have more intuitive appeal than observed-rate composite scores. Facilities can be profiled based on more policy-relevant measures than point estimates of composite scores, and interval estimates can be calculated without assuming the QIs are independent. Usually, shrunken-rate composite scores in 1 year are better able to predict the observed total number of QI events or the observed-rate composite scores in the following year than the initial year observed-rate composite scores.

Conclusion

Shrinkage estimators can be useful when a composite measure is conceptualized as a formative construct.

The number of indicators developed to measure quality of patient care has expanded rapidly as pressures to improve quality have increased. Some of these indicators are different measures of the same underlying construct. Many of the indicators, however, measure different dimensions of quality that reflect the multiple objectives of provider organizations and the needs of diverse stakeholders. Individual indicators are useful in identifying specific areas for improvement and tracking improvement progress; however, to assess overall performance, it is useful to aggregate individual quality indicators (QIs) into a composite measure (Institute of Medicine 2006). A composite measure provides a useful summary of the extent to which management has created a culture of quality and designed processes to ensure quality throughout the organization. It allows senior leaders to benchmark their organization's performance against high-performing organizations and to monitor changes over time. For individual patients, who must select one facility for their care, a composite measure is a way of combining diverse information into one more easily processed number. And composite measures allow researchers to identify and then study characteristics of high-performing organizations, departments, or teams and to develop models to guide organizational transformation.

When one considers a composite measure of quality, one often has in mind an underlying latent construct called “quality” that is manifested in the particular QIs. This latent construct, called a reflective construct to indicate that the construct is reflected in the individual QIs (in the same sense that a student's underlying mathematics ability is reflected in his or her scores on a series of mathematics tests), is one type of composite measure (Edwards and Bagozzi 2000). When conceptualized as a reflective construct, the direction of causality is from the construct to the QIs, that is, the QIs are high or low because the underlying construct “quality” is good or bad. The implication of this conceptualization is that the QIs should be highly correlated. In this article, we consider 28 QIs derived from the minimum dataset (MDS) that are used to evaluate nursing home care (Zimmerman 2003). Though subsets of the MDS-based QIs may be correlated, in general there is a relatively low correlation across most of the MDS indicators (Mor et al. 2003).

Alternatively, a composite measure can be conceptualized as a formative construct. In this case, the construct is formed from or defined by the individual QIs, usually by taking a weighted or unweighted average of the QIs (Nardo et al. 2005). One would not necessarily expect individual QIs that comprise a formative construct to be correlated. In fact, individual QIs are often selected to broaden the definition of quality and reflect its different dimensions, not to add measures that are highly correlated with existing measures. In this article, we treat the composite measure calculated from the individual QIs as a formative construct. We use opportunity-based weights to combine the individual QIs, the approach used by CMS in its pay-for-performance program (Premier 2003), as well as several alternative weighting schemes (AHRQ Quality Indicators 2008a,b).

A challenge when examining individual QIs across a range of facilities is that sample sizes are often small, and they vary across facilities. In this situation, shrinkage estimators can be of value (Efron and Morris 1977; Christiansen and Morris 1997; Normand, Glickman, and Gatsonis 1997; Burgess et al. 2000; Greenland 2000; Landrum, Bronskill, and Normand 2000; Arling et al. 2007; O'Brien et al. 2007; and Staiger et al. 2009). Rather than estimating the “true” proportion experiencing a QI event at a particular facility as the observed proportion at that facility, a simple shrinkage estimator estimates the “true” proportion at a facility as the weighted average of the observed proportion at the facility and the observed proportion at some larger set of facilities that include the particular facility. As a result, the estimate of the “true” proportion is “pulled” or “shrunken” toward the overall proportion in the larger set of facilities. The amount of shrinkage depends both on the sample size at the particular facility and the extent to which performance differs across facilities. The articles referenced above discuss the advantages of these types of shrinkage estimators and several papers have applied shrinkage estimators to individual MDS-based QIs (e.g., Berlowitz et al. 2002; Arling et al. 2007).

The 28 QIs we consider, often called the Nursing Home Quality Indicators, are provided to nursing homes through the National Automated Quality Indicator System and used by regulators as a preliminary step in the certification process (Castle and Ferguson 2010). These indicators are routinely monitored by the Veterans Health Administration (VA) and sent monthly to each VA long-term care facility (called Community Living Centers, CLCs).

For VA CLCs, we first calculate a composite score from the observed rate of each of the 28 QIs at each facility. We then use a Bayesian multivariate normal-binomial model to calculate a shrunken estimate of the rate of each QI at each facility, which are combined into a composite score. We consider two questions: (1) to what extent are the composite scores and facility rankings different when the composite score is calculated from shrunken estimates rather than observed rates? and (2) to what extent are predictions of next year's performance better when based on shrunken estimates rather than observed rates? The last question is particularly important because the estimate best able to predict the future is the estimate that best approximates persistent levels of performance over time.

Methods

Quality Indicators

As part of the Omnibus Budget Reconciliation Act of 1987, nursing homes were required to use a standardized data collection instrument, the Resident Assessment Instrument (RAI), for quarterly patient assessments and care planning. The MDS, a core component of the RAI, is a summary assessment of each long-stay nursing home resident, that is, those in the nursing home for at least 90 days. The 28 MDS-based QIs we consider consist of 24 separate indicators, four of which are stratified into high-risk versus low-risk categories (see footnote, Table 1). For some indicators, there are eligibility criteria for inclusion in the denominator. Hence, within a facility, the denominator for each indicator may differ. We consider the indicators calculated from the last full MDS assessment on each patient in the fiscal year. We use data from fiscal years (FY) 2005 (October 2004 through September 2005) through FY 2008.

Table 1.

Illustrating Shrinkage Estimators Based on the Multivariate Normal-Binomial Model

Quality Indicator*	Facility Observed Rate	Facility Shrunken Rate	Population Rate	Denominator
1	0.000	0.0046	0.0076	16
2	0.000	0.0728	0.1022	18
3	0.000	0.0313	0.0629	13
4	0.200	0.0942	0.2660	5
5	0.000	0.0616	0.1002	18
6	0.000	0.0283	0.0424	18
7	0.889	0.8321	0.7283	18
8	0.000	0.0379	0.0586	14
9	0.182	0.2240	0.3228	11
10		0.7978	0.8601	0
11	0.000	0.1693	0.1028	3
12	0.278	0.2008	0.1424	18
13	0.000	0.0043	0.0016	18
14	0.056	0.0742	0.0770	18
15	0.111	0.1662	0.1383	18
16	0.000	0.1015	0.0658	18
17	0.000	0.0031	0.0027	18
18	0.000	0.0513	0.0636	18
19	0.176	0.1433	0.1333	17
20	0.111	0.0749	0.0773	18
21	0.000	0.0972	0.1552	17
22		0.3641	0.4586	0
23	0.176	0.1323	0.1927	17
24	0.000	0.0446	0.0418	18
25	0.000	0.0045	0.0055	18
26	0.000	0.0167	0.0250	18
27	0.125	0.0912	0.0416	8
28	0.400	0.3155	0.1786	10

^*QI 1, incidence of new fractures; QI 2, prevalence of falls; QI 3, prevalence of behavioral symptoms affecting others, high risk; QI 4, prevalence of behavioral symptoms affecting others, low risk; QI 5, prevalence of symptoms of depression; QI 6, prevalence of depression with no antidepressant therapy; QI 7, use of nine or more different medications; QI 8, incidence of cognitive impairment; QI 9, prevalence of bladder or bowel incontinence, high risk; QI10, prevalence of bladder or bowel incontinence, low risk; QI11, prevalence of occasional or frequent bladder or bowel incontinence without a toileting plan; QI12, prevalence of indwelling catheters; QI13, prevalence of fecal impaction; QI14, prevalence of urinary tract infection; QI15, prevalence of weight loss; QI16, prevalence of dehydration; QI17, prevalence of tube feeding; QI18, prevalence of bedfast residents; QI19, incidence of decline in late-loss ADLs (activities of daily living); QI20, incidence of decline in ROM (range of motion); QI21, prevalence of antipsychotic use in the absence of psychotic or related conditions, low risk; QI22, prevalence of antipsychotic use in the absence of psychotic or related conditions, high risk; QI23, prevalence of any anxiety/hypnotic use; QI24, prevalence of hypnotic use more than two times in the last week; QI25, prevalence of daily physical restraints; QI 26, prevalence of little or no activity; QI27, prevalence of stage 1–4 pressure ulcers, high risk; QI28, prevalence of stage 1–4 pressure ulcers, low risk.

VA Community Living Centers

Between FY05 and FY07, the VA operated 132 CLCs. In this analysis, we consider 112 of these facilities that in FY07 met the following volume criteria: at least one of the 28 QIs had a denominator of at least 10 residents (implying there were at least 10 long-stay residents in the facility) and at least a third of all residents were long-stay (based on average daily census). In FY08, there were several facility closures. Hence, we tend to focus on data from the FY05 to FY07 period. However, when making predictions for the next year, we also use FY08 data.

Weights Used to Create the Composite Score

A number of different weighting schemes have been proposed to combine individual quality indicators into a composite score. We consider the following:

1. Facility-specific opportunity-based weights: Let Y_ij = the number of QI events of type i in facility j, for i = 1,…,28 QIs; j = 1,…,112 facilities; and n_ij = the number of patients eligible for QI event i in facility j. 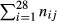= total “opportunities for a QI event to occur in facility j and 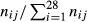= the proportion of total opportunities that are associated with QI i in facility j. The ratio 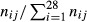is the opportunity-based weight associated with QI event i in facility j. We denote this ratio by O_ij. The composite score for facility 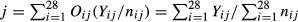. Thus, the composite score for facility j is the sum of the number of QI events at the facility divided by the sum of the opportunities to develop QI events. We denote the composite score for facility j based on observed rates and facility-specific opportunity-based weights by .

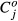2. Population-derived opportunity-based weights: Some see an advantage in a single set of weights that is used by all facilities and prefer calculating opportunity-based weights from the sum of the “opportunities” across facilities. Thus, the weight for QI i = ∑_jn_ij/∑_ijn_ij. We call these weights population-derived opportunity-based weights.

3. Equal weights: A weight of (1/24 = 0.042) is given to each QI that is not stratified and 0.021 to the high- and low-risk categories that comprise the stratified QIs.

4. Population-derived numerator-based weights: The weight for QI i in each facility = ∑_jY_ij/∑_ijY_ij.

As Booysen (2002) notes, “no weighting system is above criticism.” We agree with Babbie (1995) that, in the absence of strong justification for differential weights, equal weighting should be the norm. The weights most clearly consistent with the intent of equal weighting are facility-specific opportunity-based weights. As the resulting composite can be calculated as the sum of the number of residents experiencing each QI event divided by the sum of the number of residents at-risk for each QI event, a decrease in one QI event, regardless of the specific indicator, has the same impact on the composite. In addition, the composite resulting from opportunity-based weights can be interpreted as the likelihood an average resident experiences a QI event. For these two reasons, we prefer facility-specific opportunity-based weights and emphasize results using these weights in what follows. To the extent most residents are eligible for most of the QIs (which is the situation in our case), population-derived opportunity-based weights and equal weighting will result in composites similar to those resulting from facility-specific opportunity-based weights. Population-derived numerator-based weights assign higher weights to more prevalent QIs. Hence, results using these weights are likely to be different from the other sets of weights to the extent there are large differences in the prevalence of certain QIs.

To calculate the 95 percent confidence interval for the composite score for a particular facility when facility-specific opportunity-based weights are used, we need the variance of 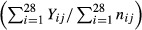. When only facility-level data are available, this variance can only be calculated under the assumption that the QIs are independent (Teixeira-Pinto and Normand 2008). The correlation matrix for FY07 data included in Supplemental Material shows that although about half the correlations of QI rates are between -0.10 and 0.10, 25 percent of the correlations are >0.20 or <−0.20, and a little over 20 percent are negative.

Bayesian Multivariate Normal-Binomial Model

Let p_ij = “true” rate of QI event i, i = 1,…,28, for facility j, j = 1,…,112.

These are the “shrunken” rates. We use a multivariate normal distribution to model these rates. The data for the model are the observed facility-level Y_ijs and the n_ijs defined above. The model is

where N₂₈ (γ, Σ) is a 28-dimension multivariate normal distribution with mean vector γ and covariance matrix Σ. We specify a noninformative multivariate normal prior for the mean vector γ and use a Wishart distribution for the inverse covariance matrix T = Σ⁻¹. To calculate the shrunken composite score of quality at facility j, we use the posterior mean (conditional on the data) of the facility-specific opportunity-based weighted sum 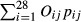. We denote the composite score for facility j based on shrunken rates by 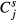. We also calculate the composite score using the other weighting schemes.

We estimate model parameters using Gibbs sampling as implemented in WinBUGS (Spiegelhalter et al. 2003). This Markov Chain Monte Carlo (MCMC) estimation method generates samples of model parameters from the posterior distribution of the parameters, given the data and prior distributions of the parameters. Because we place noninformative priors on the parameters, the posterior distributions are driven by the data. (See Supplemental Material for the WinBUGs program and specification of the noninformative priors.) We use as point estimates of the parameters the average of the values from the Gibbs samples. We also report 95 percent credible intervals for parameter estimates. These intervals are the range within which we are 95 percent sure the true value of the parameter lies. These intervals take into account correlation among the QIs.

Analysis

We calculate composite scores from both shrunken and observed QI rates for FY05, FY06, FY07, and FY08. When not otherwise specified, the composite scores are calculated using facility-specific opportunity-based weights. Policy makers and others often identify high- and low-performing facilities as those ranked in the top or bottom decile or quintile based on these types of point estimates of parameters. However, facility rankings are very unstable (Goldstein and Spiegelhalter 1996). One advantage of using MCMC simulation to estimate parameters is that useful statistics in addition to point estimates can be calculated. We illustrate this by calculating the probability each facility, based on its shrunken-rate composite score, is in the top or bottom quintile (i.e., among the top or bottom 22 facilities) and then rank facilities based on these probabilities. We show these probabilities for FY07, as well as the observed-rate and shrunken-rate composite scores and ranks for facilities with greater than a 50 percent chance of being in the top and bottom quintiles; that is, it is more likely than not they are in the quintile. To further profile facilities, we show the 95 percent credible intervals for the FY07 shrunken-rate composite scores and the 95 percent confidence intervals for the observed-rate composite scores, and compare facilities identified as statistically significantly above or below average based on these intervals.

To evaluate the fit of the multivariate normal-binomial model, we compare the number of QI events of type i in facility j in a specific year t to the number predicted by the model. To indicate year, we add a subscript t to the variables. Specifically, let p_ij(t) = estimated value of p_ij in year t, n_ij(t) = the number of patients eligible for QI event i in facility j in year t, and Y_ij(t) = the number of QI events of type i in facility j in t. We calculate 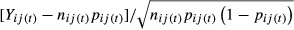, a measure of the number of standard deviations that observed differs from expected. If our model is reasonable, approximately 95 percent of the data should be within two standard deviations of what is expected.

Our main interest is in evaluating how well a composite score based on this year's data is able to predict next year's data. There are two types of data that one might reasonably predict: one, the number of QI events that occur next year; and two, the composite rate next year. Predicting the number of QI events is most reasonable for those composite scores that approximate the likelihood of developing a QI event, which, as noted above, is the case for all of the weighting methods except numerator-based weights. Predicting next year's composite rate is appropriate for all methods. When next year's composite rates are predicted, a difference in rates is treated the same regardless of facility size; when next year's QI events are predicted, a difference in rates contributes more to the error when it is from a larger facility.

When predicting cases, the prediction error for facility j in time period (t + 1) when using shrunken rates from time period t equals 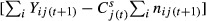; when predicting rates, the prediction error equals 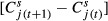. There are comparable prediction errors when making predictions based on the observed rates in time period t (calculated using 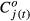). We summarize the errors two ways: one, the square root of the average of the sum of the squared errors over the j facilities; and two, the average of the sum of the absolute values of the errors over the j facilities. We repeat this analysis for the different weighting approaches. We also consider comparable errors when predicting individual QI observed numbers of events and rates in each facility in time period (t + 1) from individual QI rates (as opposed to composite rates) in time period t.

Results

Before reporting overall results, we illustrate the way in which the Bayesian multivariate normal-binomial model “shrinks” estimates. Table 1 shows for each QI in one facility the observed rate, the shrunken rate, and the number of eligible residents; it shows for each QI the observed rate across all facilities. Consider QI 1. There were no cases observed in this facility in FY07. Over all facilities, 7.6 residents per 1,000 experienced this QI event. Is it reasonable to believe, based on the 16 eligible cases in this facility, that the “true” rate for the facility is zero? A Bayesian would say “no.” The facility probably is better than average with respect to this QI, but it is probably not perfect. The shrunken estimate, which gives some weight to observed rate of zero and some to the population rate of 7.6/1,000, is 4.6/1,000, which reflects this compromise. QI 2 and QI 3 indicate the same type of shrinkage. QI 7 and QI 12 also indicate typical shrinkage, but in this case, the shrunken estimate is between a high observed rate and a lower population rate. The actual amount of shrinkage in each of these situations depends on the sample size for the QI at the facility and the amount of variation in the QI rates across facilities. When there is more variation across all facilities, one trusts the population rate somewhat less as a reasonable estimate for a specific facility and hence there is less shrinkage; when there is little variation across facilities, one trusts the population rate more and there is more shrinkage.

QI 4 illustrates “nontypical” shrinkage—the shrunken estimate is not between the observed rate and the higher population rate but significantly lower than the observed rate. The reason for this is because of the nature of the variance/covariance matrix for the 28 QIs. Shrinkage depends not just on the population rate of a particular QI but on performance on other QIs with which the particular QI is correlated. QI 4 is highly correlated with QI 5 (0.64) and QI 6 (0.52) (numbers in parentheses are the correlation coefficients). The observed facility rate on both of these QIs is zero, well below the respective population rates. The low value of the shrunken estimate for QI 4 reflects these very low rates of correlated QIs. QI 16 provides another “nontypical” example in which there is shrinkage past the overall mean. In this case, the observed rate is below the population rate, but the shrunken rate is above the population rate. QI 16 is relatively highly correlated with QI 18 (0.32) and QI 28 (0.37). The observed rate for QI 28 is very high relative to population rate. QI 18 has a low observed rate. However, it is correlated with QI 19 (0.28), QI 27 (0.27), and QI 28 (0.35). All three of these QIs have observed rates above the population rates, which contribute to the high shrunken estimate for the true rate of QI 16 at this facility.

Finally, note QIs 10 and 22, where there were no eligible cases. This is a missing data problem. If these QIs had zero correlation with other indicators, the shrunken estimate would be the population rate. In fact, it is somewhat lower, reflecting that the QIs with which these indicators are correlated have somewhat lower rates than the population rates.

Model predictions are consistent with the data. The percentage of cases in which the observed number of residents experiencing each QI in each facility in a particular year is more than two standard deviations from model-predicted values for that year are, for FY05 through FY08, as follows: 2.6, 5.7, 5.8, and 3.4 percent.

Table 2 shows those facilities with at least a 50 percent chance of being in the top quintile (Part A) and bottom quintile (Part B), as well as the facilities’ shrunken-rate and observed-rate composite scores and ranks. In Part A of the Table, comparing the 13th and 15th ranked facility based on shrunken rates highlights the value of the probability information: though the shrunken rates are very similar, the 13th ranked facility has over a 92 percent chance of being in the top quintile, while the 15th ranked facility, which has a much smaller sample size, has only a 71 percent chance. The probabilities provide in one number not only a basis for ranking but also a measure of confidence that the facility really is a top-quintile performer. The top 23 facilities based on shrunken-rate composite scores are the same facilities that have over a 50 percent chance of being in the top quintile, though the order of the facilities differs somewhat by ranking approach. Twenty-one of the top 23 facilities based on the observed-rate composite score are among the 23 facilities with the highest estimated probability of being in the top quintile. The two facilities not included are small and, despite point estimates that place them in the top quintile, in fact have under a 35 percent chance of being in that quintile. The same pattern can be seen for facilities with the highest probability of being in the bottom quintile.

Table 2.

Top (Bottom)-Ranked Facilities Based on the Probability the Shrunken-Rate Composite Score2 Is in the Top (Bottom) Quintile

A. 23 Facilities with Greater Than a 50% Chance the Shrunken-Rate Composite Score Is in the Top Quintile
Probability in Top Quintile	Shrunken Rate	Shrunken Rank	Observed Rate	Observed Rank	Number of Cases
1.000	0.068	1	0.066	1	222
1.000	0.081	2	0.080	2	149
1.000	0.089	3	0.083	3	87
0.996	0.095	4	0.087	4	77
0.993	0.100	12	0.103	22	109
0.993	0.099	10	0.096	11	135
0.990	0.098	8	0.098	13	174
0.989	0.097	6	0.091	7	104
0.982	0.099	9	0.096	9	69
0.981	0.096	5	0.087	5	29
0.957	0.097	7	0.098	14	55
0.955	0.100	14	0.099	17	86
0.948	0.099	11	0.100	19	93
0.921	0.100	13	0.098	15	44
0.870	0.103	18	0.102	21	64
0.808	0.106	19	0.104	23	137
0.778	0.102	16	0.090	6	23
0.708	0.101	15	0.099	16	10
0.667	0.103	17	0.097	12	23
0.659	0.106	20	0.101	20	36
0.558	0.109	22	0.106	25	37
0.542	0.107	21	0.093	8	10
0.512	0.109	23	0.105	24	28

B. 19 Facilities with Greater Than a 50% Chance the Shrunken-Rate Composite Score Is in the Bottom Quintile
Probability in Bottom Quintile	Shrunken Rate	Shrunken Rank	Observed Rate	Observed Rank	Number of Cases
1.000	0.169	108	0.176	109	69
1.000	0.171	110	0.183	110	68
1.000	0.184	112	0.190	112	25
1.000	0.167	106	0.167	104	82
0.992	0.168	107	0.173	107	60
0.988	0.170	109	0.173	108	35
0.986	0.173	111	0.187	111	20
0.955	0.164	104	0.171	106	20
0.902	0.156	102	0.154	96	157
0.865	0.164	105	0.168	105	26
0.841	0.155	100	0.161	103	74
0.810	0.153	98	0.155	99	154
0.742	0.157	103	0.153	94	35
0.713	0.155	101	0.153	95	24
0.690	0.153	99	0.154	98	51
0.638	0.151	97	0.150	91	225
0.540	0.149	95	0.158	102	71
0.534	0.149	94	0.154	97	130
0.511	0.150	96	0.150	92	79

^*Composite scores calculated using facility-specific opportunity-based weights.

The statistics on the shrunken-rate and observed-rate composites are fairly similar across years. Using FY07 data to illustrate, minimum, median, and maximum rates using shrunken rates were 0.068, 0.127, and 0.184; using observed rates, they were 0.066, 0.124, and 0.190, respectively. As expected since extreme rates are shrunken toward the average, the range of composite scores when using shrunken rates is somewhat smaller than when using observed rates. When using the shrunken-rate composite instead of the observed-rate composite, 40 facilities have lower ranks (indicating worse performance). For these facilities, the median change in rank is 6; the 75th and 90th percentile change and the maximum change are 9, 13, and 33. Fifty-five facilities have higher ranks. For these facilities, the median change in rank is 4; the 75th and 90th percentile change and the maximum change are 8, 11, and 20.

Figure 1A shows the point estimates and 95 percent credible intervals for the shrunken-rate composite scores in FY07. There are 27 facilities where the upper end of the 95 percent credible interval is below the population average, indicating these are high-performing facilities. There are 28 facilities where the lower end of the 95 percent credible interval is above the population average, indicating these are low-performing facilities. The high-performing facilities are clearly distinguishable from the low-performing facilities. However, many of the high- and low-performing facilities are not clearly distinguishable from subsets of the average-performing facilities. Figure 1B shows the point estimates and 95 percent confidence intervals for the observed-rate composite scores (facilities are portrayed in the same order as in Figure 1A). On average, the 95 percent confidence intervals are about 12 percent larger than the 95 percent credible intervals. Thirty facilities are identified as high performers (including 24 of the 27 facilities identified using the 95 percent credible intervals), and 30 facilities are identified as low performers (including 25 of the 28 facilities flagged as low performers using the 95 percent credible intervals).

Figure 1.

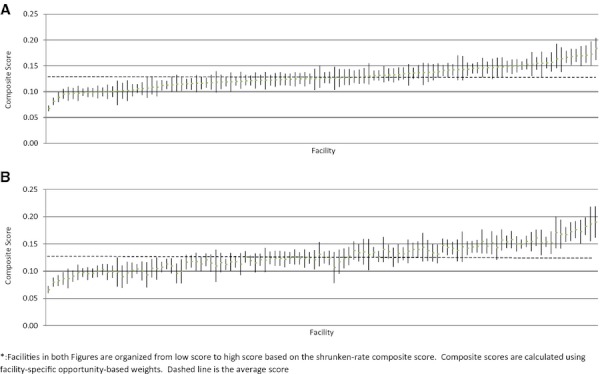
(A) Shrunken-Rate Composite Scores and 95% Credible Intervals, FY07. (B) Observed Rate Composite Scores and 95% Confidence Intervals, FY07. *Facilities in both figures are organized from low score to high score based on the shrunken-rate composite score. Composite scores are calculated using facility-specific opportunity-based weights. Dashed line is the average score.

Table 3A shows the percentage reduction in error when making predictions using the shrunken-rate composite score instead of the observed-rate composite score and, in parentheses, the size of error when using the shrunken-rate composite. For the first three weighting schemes, with one exception (predictions of FY06 data from FY05 composite scores calculated using facility-specific opportunity-based weights), there is a smaller prediction error when the composite score is based on shrunken rates. When numerator-based weights are used, the value of the shrunken-rate composite is less apparent. (In Supplemental Materials, we show scatter plots of the errors when predicting number of cases using shrunken-rates vs. observed rates for the two ways of measuring error and for the three time periods examined.) As expected, the actual sizes of the errors when predicting cases are very similar when facility-specific opportunity-based weights, population-derived opportunity-based weights, and equal weights are used. This reflects the fact that with the exception of the QIs stratified into high and low risk, most residents are eligible for most of the QIs. As a result, none of the weights associated with a QI are above 0.052 for any of these approaches. In contrast, using numerator-based weights, a weight of 0.268 is assigned to QI 7 (use of 9 or more medications) and 0.077, 0.063, and 0.059 to the next three most prevalent QIs (QI 9, QI 4, and QI 10). It is not surprising that there are very large errors when a composite calculated using numerator-based weights is used to predict the number of QI events next year. It is interesting that even when numerator-based weight composites are used to predict next year's numerator-based weight composite, the errors are larger than when the other weighting approaches are used.

Table 3.

Predicting Next Year's Data: Comparison of Errors Using Shrunken and Observed Quality Indicator Rates

	Predicting FY06 from FY05 Estimates	Predicting FY07 from FY06 Estimates	Predicting FY08 from FY07 Estimates
A. Composite scores: Percentage reduction in error (size of error) using shrunken-rate composite*
Facility-specific opportunity-based weights
Mean squared error: cases	−1.9 (32.8)	2.5 (24.6)	4.6 (40.5)
Mean absolute deviation: cases	−2.0 (24.2)	6.7 (17.4)	4 (31.9)
Mean squared error: rates	2.9 (.021)	7.9 (.017)	10.0 (.020)
Mean absolute deviation: rates	−1.3 (.017)	9.0 (.013)	8.1 (.016)
Population-derived opportunity-based weights
Mean squared error: cases	0.1 (33.0)	4.4 (25.3)	5.2 (40.3)
Mean absolute deviation: cases	2.7 (24.2)	7.1 (17.5)	5.2 (31.2)
Mean squared error: rates	4.2 (.021)	7.1 (.017)	10.3 (.020)
Mean absolute deviation: rates	2.1 (.016)	9.0 (.013)	9.1 (.016)
Equal weights
Mean squared error: cases	3.4 (60.0)	5.1 (31.3)	16.5 (36.3)
Mean absolute deviation: cases	2.1 (43.3)	5.9 (22.3)	17.6 (28.5)
Mean squared error: rates	7.3 (.028)	8.0 (.021)	17.8 (.018)
Mean absolute deviation: rates	7.3 (.022)	6.5 (.017)	19.6 (.014)
Population-derived numerator-based weights
Mean squared error: cases	0.3 (393)	−0.2 (390)	1.7 (594)
Mean absolute deviation: cases	2.7 (332)	−1.6 (333)	−0.0 (520)
Mean squared error: rates	−0.0 (.035)	−1.2 (.227)	0.1 (.226)
Mean absolute deviation:	3.3 (.028)	−2.2 (.224)	−1.2 (.220)
B. Individual quality indicators in a facility: Percentage reduction in error*
Mean squared error: cases	3.1	−0.9	3.0
Mean absolute deviation: cases	2.4	16.3	1.7
Mean squared error: rates	4.2	2.8	3.7
Mean absolute deviation: rates	15.6	16.1	9.5

^*Percentage reduction in error = (observed-rate error − shrunken-rate error)/observed-rate error. A negative value indicates the observed-rate error is smaller than the shrunken-rate error.

Table 3B shows the percentage reduction in error when this year's shrunken rate for QI i in facility j instead of the observed rate for QI i in facility j is used to predict next year's observed number of QI events and QI rates for QI i in facility j. For the two types of errors and the 3 years of analysis, with one exception (squared errors in the FY06/FY07 analysis when predicting cases), shrunken-rate composites have lower prediction errors. (In Supplemental Materials, we show scatter plots of the individual QI/facility prediction errors when predicting cases using shrunken rates vs. observed rates composites to make the predictions.)

Discussion and Conclusions

Shrinkage estimators, as illustrated above, have a number of advantages. First, they can be thought of as a way of adjusting or “smoothing” observed rates to reflect the reliability of the observed rates. The adjustment takes into account the relationship between the observed rate of each QI in a facility and the population rate of that QI, as well as the observed rate and population rate of other QIs with which the QI is correlated. As we demonstrate in Table 1, shrinkage estimators are particularly attractive when observed rates are from small facilities. Second, the MCMC method used to estimate model parameters also allows estimation of statistics that may be of more policy relevance than point estimates of rates. We illustrate this by estimating the probability that each facility is in the top or bottom quintile based on their shrunken-rate composite score. When point estimates are used, pretty much the same facilities are identified as being in the top and bottom quintile whether based on shrunken-rate composites or observed-rate composites. However, the likelihood that facilities ranked in the top or bottom quintile are actually in that quintile differ. In a pay-for-performance program, one might well want to increase payments to top-quintile facilities that have higher likelihoods of actually being in the top quintile and reduce penalties of bottom-quintile facilities that have smaller likelihoods of actually being in the bottom quintile. Third, the 95 percent intervals associated with shrunken-rate estimates are credible intervals, that is, intervals within which there is a 95 percent chance the estimated parameter lies. This type of interval estimates is more meaningful than the frequentist 95 percent confidence interval and is in fact the way in which many people incorrectly interpret a 95 percent confidence interval. Also, using MCMC methods, the 95 percent credible interval can be calculated without assuming QIs are independent. Finally, the shrunken-rate composite scores fairly consistently have smaller prediction errors than observed-rate composite scores. The difference in errors is usually not large, but it does hold up across years, ways of measuring errors, and, with the exception of numerator-based weights, weighting approaches. Also, when predicting facility-specific individual QI events, shrunken rates usually do better. Staiger et al. (2009) have shown that you are better able to predict rates for an individual surgery if you use a composite measure that takes into account other surgeries with which the particular surgery is correlated. We found the same thing for the MDS-based QIs: you can predict individual QIs better if you take into account other QIs with which the particular indicator is correlated.

It is worth noting that because only facility-level data were available, we were not able to examine composite measures created by aggregating individual-level experiences. For example, we could not analyze the number of individuals experiencing a QI event or average number of QI events per individual. Though most major profiling efforts do not report measures created by aggregating individual-level experience, it would be interesting to examine the value of shrunken estimates for these types of composite measures.

Our use of a Bayesian multivariate normal model was motivated by the work of Landrum, Normand, and Rosenheck (2003), who, like us, estimated shrunken rates for a number of quality measures, which were then combined into composites. O'Brien et al. 2007 used a similar approach to combine measures from four domains into a composite measure for evaluating cardiac surgery. For the policy and nontechnical reader, we have attempted to provide more understanding of the way shrinkage works in these types of models; we show that predictions from the multivariate normal-binomial model are consistent with the data, and as noted, we have compared predictions of the future using both shrunken and observed rates to calculate the composite, something that at least to our knowledge has not been done when constructing composite measures of performance.

Our results cannot be generalized beyond the particular setting and quality measures we considered. Nevertheless, they do suggest the potential of using shrinkage methods when calculating a composite measure that is conceptualized as a formative construct.

SUPPORTING INFORMATION

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Data S1: Scatterplot of Squared Errors and Absolute Value Errors of Predictions of Indidivual QI/Facility Rates Using Shrinkage Estimators and Observed Rates.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.