Figure 2.
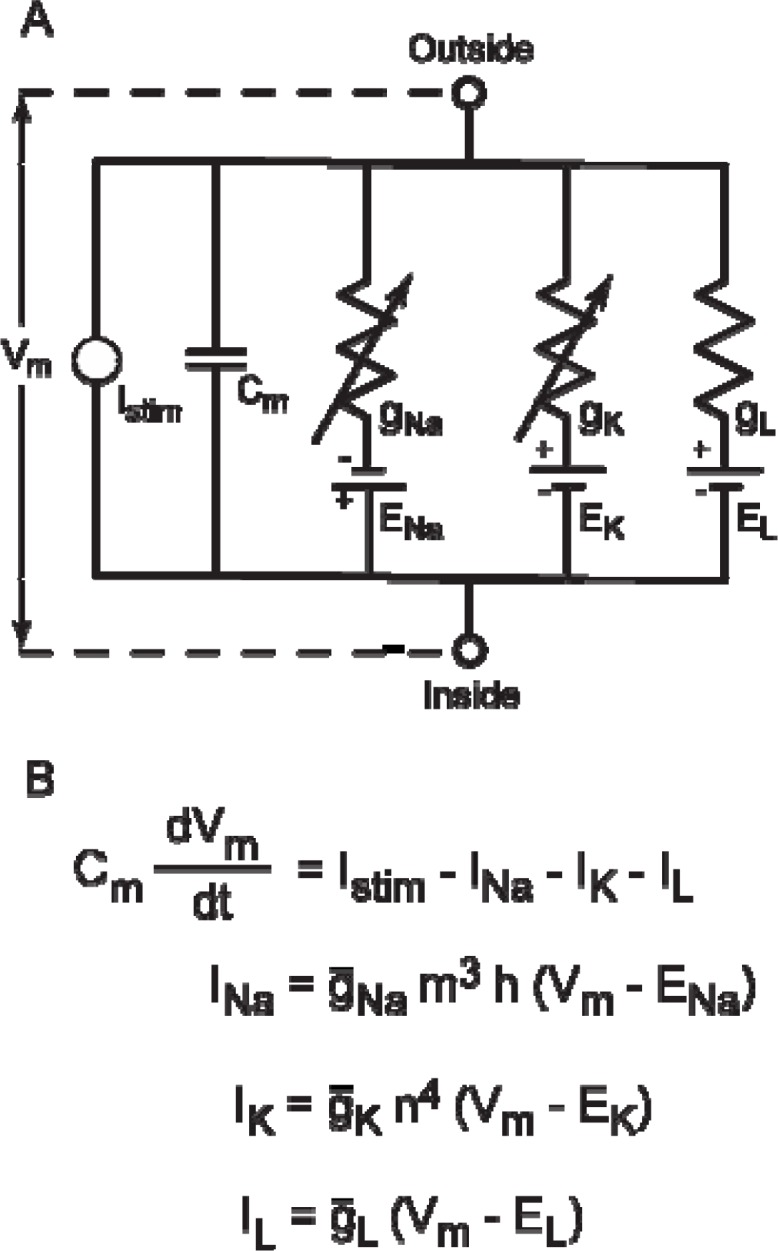
Equivalent electric circuit for HH model. A: Hodgkin and Huxley pioneered the concept of modeling the electrical properties of nerve cells as electrical circuits. The variable resistors represent the voltage- and/or time-dependent conductances. (Note, conductances can also be regulated by intracellular ions or second messengers, see Fig. 7.) The HH model has three ionic conductances: sodium (gNa), potassium(gK) and leak (gL). The batteries represent the driving force for a given ionic current. CM represents the membrane capacitance. Istim represents an extrinsic stimulus current that is applied by the experimenter. B: A few of the equations in the HH model. The ordinary differential equation (ODE) that describes the membrane potential (Vm) of the model contains the ensemble of ionic currents that are present. The HH model is relatively simple and contains only three ionic currents. Other models may be more complex and contain many additional ionic currents in the ODE for the membrane potential (e.g. see Butera et al., 1995; Av-Ron and Vidal, 1999). The ionic currents are defined by a maximal conductance (g̅), a driving force (Vm – Eion), and in some cases activation (m, n) and/or inactivation (h) functions. These equations illustrate many of the parameters that students may wish to vary. For example, values of g̅ can be varied to simulate different densities of channels or the actions of drugs that block conductances. Similarly, values of Eion can be changed to simulate changes in the extracellular concentrations of ions (see Av-Ron et al., 1991).
