A CONTINUOUS-TIME MARKOV CHAIN APPROACH ANALYZING THE STAGES OF CHANGE CONSTRUCT FROM A HEALTH PROMOTION INTERVENTION

Abstract

The Transtheoretical Model of behavior change is often used in longitudinal research of health-related outcomes. This model includes a construct called stage of change, which is a hypothesized concept of progression for individuals trying to modify their behavior. Project HOME (Healthy Outlook on the Mammography Experience), a population-based randomized group intervention trial sought to identify factors associated with subject changes in stage, from precontemplation to contemplation and from contemplation to action. The aims of this paper are to extend Li and Chan’s Markov model approach to handle multiple covariates that include both continuous and binary variables. An empirical study was conducted to evaluate the accuracy of the estimators. The model was then applied to the Project HOME data. Specifically, we present a continuous-time Markov chain approach to examine covariates and their effect on the dynamics of the changes in stage. This model can be used by researchers to more fully describe transitions in data.

1. Introduction

The Transtheoretical Model (TTM) is used to predict behavior change. Longitudinal studies using the TTM have shown individuals’ behavior as a progression through five stages of change. Stages of change are a hypothesized ordered concept of progression for individuals trying to modify their behavior [6] categorized into precontemplation, contemplation, preparation, action, and maintenance. Precontemplation is the stage in which individuals do not have any intention to perform a behavior in the near future; contemplation is the stage in which individuals are considering changing a behavior, but may be ambivalent; preparation is the stage in which individuals intend to change their behavior and are making plans to do so; action is the stage in which individuals have made successful attempts to change their behavior in the recent past; and maintenance is the stage in which individuals have sustained a behavior change over time [17, 18].

The Transtheoretical Model has been supported empirically when used to predict diverse health-related outcomes including mammography screening, smoking cessation, weight control, condom use, and sunscreen use [6, 17]. In some of these studies, stage of change is measured longitudinally at multiple time points during the study.

Stage of change is typically analyzed using pairwise comparisons of binary logistic regression models or two ordinal logistic regression models of a redefined outcome variable (positive and negative directionality). For example, these techniques were used by Chamot, Charvet, and Perneger [3] in examining stages of mammography adoption. Their analysis included comparisons of binary logistic regressions (e.g., contemplation vs. precontemplation and action vs. contemplation) and two ordinal logistic regression models (precontemplation to maintenance and action/maintenance to relapse). The inadequacy of these methods is that they do not use all of the data simultaneously in one analysis, as does an application of a Markov model. But even more so, what sets a Markov model approach apart from these traditional statistical techniques is its ability to examine the relationship between time and movement; thereby providing a more complete description of the transitions in the data.

Continuous-time Markov models have been used to model natural disease histories, and applied to smoking behavior, asthma control, stages of cancer, progression of arthritis and stages of HIV infection [4, 19, 12, 1, 11, 7, 14]. In Markov models with more than two states, the examination of the effect of covariates on transition probabilities has been limited [2, 9]. To date, only one study models transitions with more than two covariates [8]. This study used Bayesian techniques for variable selection. While, all of the other published continuous-time Markov research only provides analyses using one covariate at a time [13, 19, 4], with one study mentioning the use of two simultaneous covariates but this study did not include the findings [4].

The statistical software package R has a program entitled msm that provides multi-state models to be fitted to longitudinal data. This program is very useful for modeling n-outcomes, but when one is interested in the influence of numerous simultaneous covariates on transition rates, msm has a high rate of convergence failure. Recently, an algorithm was derived for mathematically estimating parameters of a Markov model with a trinomial outcome [13]. Specifically, Li and Chan using this algorithm, developed a method to compare group differences (a single covariate) in transition for trinomial outcomes [13]. Use of this approach to analyze variables like stage of change could increase our understanding of the patterns of transitions between categories as would its implementation in msm. However, Li and Chan’s approach was limited because it did not allow for the inclusion of more than one covariate. Our aim was to extend Li and Chan’s algorithm model to handle multiple covariates that include both continuous and binary variables. To accomplish this aim, we first conducted an empirical study to evaluate the accuracy of the estimators. We then applied our model to data from Project HOME (Healthy Outlook on the Mammography Experience), a population-based group intervention trial to promote mammography screening [5, 20].

This Markov model extension allows for assessment of the influence of more than one covariate on transition rates between states, simultaneously. Moreover, a Markov-model approach provides unique information, namely, the distribution for the estimates of the probability of the next movement for the stage of change construct, and the time-to-change rate through the covariates. This approach is useful for making predictions about an individual’s future behavior in terms of time to transition and stage change.

2. Methodology

2.1. Trinomial outcome

Li and Chan derived an explicit expression of P_ij (t), the transition probabilites for a three-category outcome based on the infinitesimal matrix of a continuous-time Markov chain [13]. They further applied Markov process technique to conduct statistical inference of group dynamics of these transitions. In their analysis, the assumption is that trinomial outcomes of longitudinal studies for each subject follow a continuous-time Markov Chain with unknown transition probabilities from two groups. Li and Chan, derived three possible expressions of P_ij (t) which may be found at http://www.sph.uth.tmc.edu/course/biometry/wchan/ph1918/. From this they derived a complex algebraic form of the likelihood function in terms of elements {q_ij}, the transition intensities (the instantaneous transition rate from category i to j) of the infinitesimal matrix, where $q_{ii}=-{\displaystyle \sum _{j=1j\ne i}^3{q}_{ij}}$ and q_ij > 0, for i ≠ j.

The associated log-likelihood function was given by

$$\text{log}(L)={\displaystyle \sum _{k=1}^m{\displaystyle \sum _{l=2}^{n_k}\text{log}(P_{y_k(t_{k,l-1}),y_k(t_{k,l})}(t_{k,l}-t_{k,l-1})),}}$$ (2.1)

where y_k (t_{k, l}) is the observed category of the outcome for the kth subject at time t_{k, l}.

The current research goal was to incorporate covariates into this log-likelihood. Therefore, in this study, we chose a log transformation to link each q_ij with the linear combination of covariates, i.e.,

$$\text{log }{q}_{ij}=y_{ij}+{\displaystyle \sum _{k=1}^p{\mathrm{\beta }}_k{x}_k\text{ for }i\ne j=1,2,3\text{ and }k=1,\dots ,p.}$$ (2.2)

Note that in this model, ${(q_{ij}+q_{ij})}^{-1}={\left(e^{{\displaystyle \sum _{k=1}^p{\mathrm{\beta }}_k{x}_k}}(e^{{\gamma }_{ij}}+e^{{\gamma }_{il}})\right)}^{-1}$ is the mean duration time of category i, i ≠ j, l for the subject who has covariates (x₁, x₂, …, x_p) and $\frac{q_{ij}}{q_{ij}+q_{il}}=\frac{e^{{\gamma }_{ij}}}{e^{{\gamma }_{ij}}+e^{{\gamma }_{il}}}$ is the probability that at the end of category i, this subject moves to category j. In equation (2.2), e^γ_ij, j ≠ i is the weight that favors category j when the subject ends their stay in category i and e^−β_k is the multiplicative change of the mean duration time of any category for each unit increment of their x_k value. In order to create the log-likelihood function of this study, use equation 2.1 and the three expressions of P_ij (t) found on the webpage http://www.sph.uth.tmc.edu/course/biometry/wchan/ph1918/ substituting the exponentiation of equation 2.2 for all q_ij.

Maximum likelihood estimation (MLE) method was used to estimate the parameters in this model. Specifically, the Nelder-Mead simplex algorithm [15] was adopted for the numerical implementation of calculating the MLE. This algorithm is useful because one can avoid the differentiation of the likelihood function and hence simplify the mathematical complexity. Moreover, the Nelder-Mead simplex algorithm uses only function values and is considered robust but relatively slow. Yet, it works reasonably well for non-differentiable functions. Other optimization techniques found under the command optim for both software packages R and S Plus, such as BFGS (a quasi-Newton method) and CG (conjugate gradient method) all require at least partial derivatives to be attainable for performing MLE.

2.2. Empirical study

To examine the appropriateness of our numerical procedure in estimating the model parameters, an empirical study was conducted. For this empirical study that mimicked our real dataset, a scenario of three explanatory variables was examined, where x₁ and x₂ are dichotomous variables and x₃ is a continuous variable. To implement the procedures proposed, initial values for γ₁₂, γ₁₃, γ₂₁, γ₂₃, γ₃₁, γ₃₂, β₁, β₂, and β₃ were determined.

Explanatory variables were simulated with an n = 100 individuals with two categorical variables, each assumed to follow a Bernoulli distribution with probability equal to 0.5, and one continuous variable assumed to follow a normal distribution N(58, 2), where the outcome of each individual was assumed to follow a continuous time Markov process with 3 possible states (1, 2, or 3) based on the infinitesimal matrix calculated from the true parameters found in Table 1. The duration of the study was assumed to be six quarters with a baseline measurement, providing data at quarters 0, 2, 4, and 6.

Table 1.

True values of γ₁₂, γ₁₃, γ₂₁, γ₂₃, γ₃₁, γ₃₂, β₁, β₂, and β₃ their simulation estimates generated by the proposed method (n = 996 convergent runs)

Parameter	γ12	γ13	γ21	γ23	γ31	γ32	β1	β2	β3
True Value	0.2	0.0001	0.15	0.1	0.6	0.4	0.01	0.02	−0.03
Proposed Estimate	0.1901	0.0814	0.1812	0.1348	0.2826	0.3535	0.0097	0.0199	−0.0411
Standard Error	0.0970	0.0415	0.0924	0.0688	0.1442	0.1804	0.0049	0.0102	0.0210

Using S-Plus Version 8, datasets were created with the goal of approximately 1000 convergent simulations. 3643 simulations estimating the parameters were performed, of these 3643 simulations, 996 (27.34%) had their maximum likelihood estimate (MLE) reach convergence with a relative tolerance convergence of 0.0001; 73 out of 3643 simulations (2%) had their MLE degenerate and 2574 out of 3643 simulations (70.66%) reached a 500th iteration without convergence of their MLE. Note that a model with three covariates has a very complex likelihood function and combined with a possibility of insufficient data (n = 100 subjects) such a high nonconvergence rate is to be expected. The primary goal of the empirical study was to assess accuracy. Therefore, this study found that the biases between the mean parameter estimate and the true value were all less than 0.09, except for γ̂₃₁ = 0.2826, where the true value is 0.6.

3. Application

3.1. Study background

Project HOME measured the effect on mammography screening compliance of a tailored and targeted print intervention compared to a targeted print intervention and to a survey-only control group. Participants were women 52 years of age and older as of June 1, 2000 randomly selected from the U.S. National Registry of Women Veterans [5, 20]. Project HOME had a sample size of 3758 baseline survey respondents. Subjects were removed because of refusal (n = 564), ineligibility (n = 240), or no contact (n = 85) at the first follow-up survey, leaving a remaining sample size of 2869 subjects with a year 1 or year 2 measurement. The main outcomes for the trial was mammography screening coverage defined as completion post-intervention of one mammogram or compliance defined as completion post-intervention of two mammograms, 6–15 months apart. The Project HOME intervention took place twice, before the year 1 and year 2 surveys. The tailored-targeted intervention group received a personalized intervention based on individual responses to questions on the baseline and year 1 surveys [20]. The targeted-only intervention was based on population subgroup characteristics. In the outcome analyses, the two intervention groups were not found to be statistically different [20].

The main outcome in our analysis was stage of change. For this report, we used a three-category outcome based on the stage of change construct: precontemplation, contemplation, and action because a preventive health behavior like undergoing mammography screening has very little theoretical distinction between the preparation and contemplation stages or between the action and maintenance stages, we collapsed preparation with contemplation and maintenance with action. Stage of change was measured at baseline, year 1, and year 2 (expressed in months).

We included three covariates measured on the baseline survey; age, race/ethnicity, and intervention group status. Age was measured as a continuous variable. Race/ethnicity was collapsed into white/non-white, where non-white included African American, Asian, American Indian, and other. Because the tailored-targeted and the targeted-only groups did not differ statistically from each other, we combined the two intervention groups for this analysis. Subjects missing race/ethnicity (n = 343) were removed. There were no missing values for the race/ethnicity and age variables. The sample for the implementation of the new technique was n = 2546 (Tables 2 and 3).

Table 2.

Project HOME sample characteristic frequencies at baseline, Year 1, and Year 2 by the trinomial stage of change category

	PRECONTEMPLATION			CONTEMPLATION			ACTION
STAGE OF CHANGE	Baseline	Year 1	Year 2	Baseline	Year 1	Year 2	Baseline	Year 1	Year 2
Study Group Total	313	289	265	228	173	166	1985	1726	1680
Intervention	199	188	156	143	104	111	1337	1168	1130
Control	114	101	109	85	69	55	648	558	550
Race Group Total	296	279	285	210	158	154	1831	1603	1569
White	283	265	278	202	153	149	1756	1545	1510
Non-white	13	14	7	8	5	5	75	58	59

Table 3.

Mean Age ± Standard Deviation and sample size for project HOME participants at baseline, Year 1, and Year 2 by trinomial stage of change category

	Precontemplation	Contemplation	Action
Baseline	60.67 ± 10.05	60.87 ± 10.21	61.11 ± 9.55
	n = 313	n = 228	n = 1985
Year 1	61.89 ± 10.65	61.03 ± 10.70	60.98 ± 9.51
	n = 289	n = 173	n = 1726
Year 2	61.27 ± 10.08	61.22 ± 11.21	61.11 ± 9.61
	n = 302	n = 166	n = 1680

To analyze these data, we consider a three-state Markov model. This model includes a three-state stage of change construct outcome where all transitions between states are allowed. Assuming that the underlying process is a Markov process, we represent this model using the transition intensity matrix Q as

$$\left(\begin{array}{ccc}-(q_{12}+q_{13})& q_{12}& q_{13}\\ q_{21}& -(q_{21}+q_{23})& q_{23}\\ q_{31}& q_{32}& -(q_{31}+q_{32})\end{array}\right)$$ (3.1)

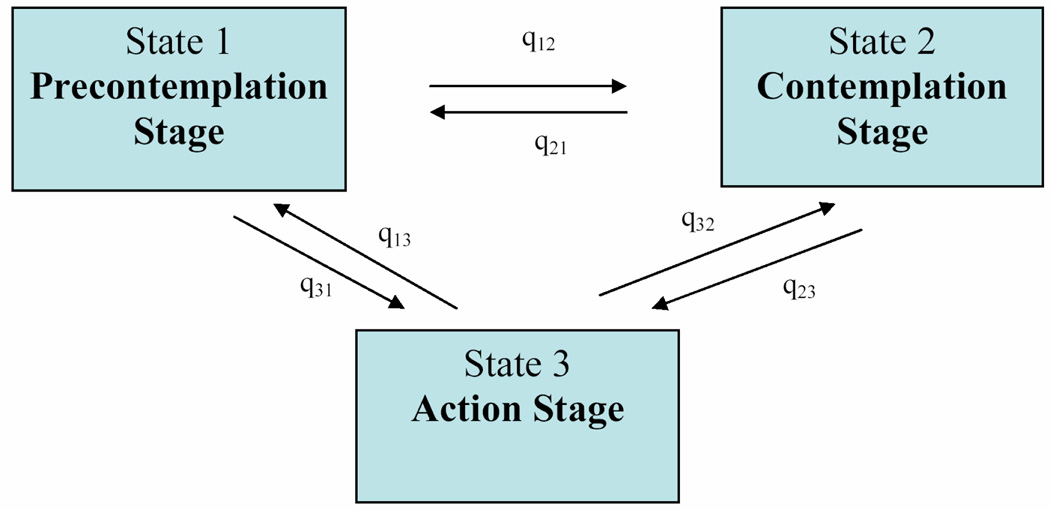
or the pattern in Figure 1.

Figure 1.

The three-state Markov model for Project Home’s stage of change construct.

3.2. Statistical analysis

This statistical analysis was an application of the new Markov technique extension for estimating gamma and beta parameters (study group status, race, and age) for the Project HOME intervention study. A description of the gamma and beta parameter estimates will be provided. Specifically with regards to the beta parameter, e^−β̂_k will provide the multiplicative change of the mean duration time of any category for each unit increment of their x_k value. Furthermore, the gamma and beta estimates will help us to better understand the dynamics of movement within the stage of change construct. Namely, the probability associated with movement and the mean duration of time spent in a stage. Lastly, the appropriateness of the model assumptions will be investigated using a split-sample validation method.

3.3. Study results

The modeling of the three-state outcome stage of change from Project HOME with three covariates did not reach convergence when using the msm command found in the statistical package R. Therefore, Table 4 provides the parameter estimates and their associated standard errors created from using the new proposed method. The standard errors were calculated from bootstrapping the individual level data with replacement 1,000 times. (This estimation technique program was performed in S Plus which is easily translatable to R.) Wald’s statistical tests were performed for H₀ : γij = 0 for i ≠ j = 1, 2, and 3 and H₀ : βi = 0 for i = 1, 2, and 3. All of the β parameter estimates (Study group status, Race, and Age) were found to be significantly different from zero. From Table 4, the mean time to stage change for the intervention group is shorter than the control group and shorter for whites compared to non-whites. Specifically, the mean time to stage change for the intervention group is 0.84 times that of the control group and the mean time to stage change for whites is 0.71 times that of non-whites. Furthermore, on average, subjects who are one year older have their mean time to change stage reduced by a multiplicative factor of 0.99.

Table 4.

Project HOME parameter estimates and implications using the newly proposed approach

Parameter							Race	Intervention
Estimate							Category	Type	Age
	γ̂12	γ̂13	γ̂21	γ̂23	γ̂31	γ̂32	β̂1	β̂2	β̂3
Proposed Estimate	−5.432	−4.971	−4.622	−3.862	−6.714	−6.305	0.340	0.179	0.007
(Standard Error)	(0.017)	(0.032)	(0.052)	(0.076)	(0.103)	(0.076)	(0.110)	(0.076)	(0.003)
eγij or e−βk	0.00438	0.00694	0.00983	0.02102	0.00121	0.00183	0.71190	0.83611	0.99317
Wald’s Statistic ${\chi }_1^2$							9.55	5.55	5.44
(P-value)							(<0.05)	(<0.05)	(<0.05)

At time of change, the transition probabilities of changing from one stage to another are presented in Table 5. Project HOME participants in the precontemplation stage were more likely to progress to action than contemplation, with probabilities 61% compared to 39%. Project HOME participants in the contemplation stage were more likely to progress to action, 68%, than to regress to precontemplation, 32%. Project HOME participants in the action stage were more likely to regress to contemplation, 60% than to precontemplation, 40%.

Table 5.

Project HOME transition probability matrix at each change

	STAGE AFTER CHANGE
STAGE BEFORE CHANGE	Precontemplation	Contemplation	Action
Precontemplation	--	0.3869	0.6131
Contemplation	0.3186	--	0.6814
Action	0.3980	0.6020	--

A unique finding of this continuous-time Markov model allows for examination of subjects’ mean duration time in the TTM stage of change. For example, Project HOME subjects spend more time in precontemplation than contemplation (Table 6). Specifically, average-age (60.6 years) white intervention subjects spend 35 months in precontemplation and 13 months in contemplation. While average-age (60.6 years) white control subjects spend 42 months in precontemplation and 15 months in contemplation.

Table 6.

Project HOME mean duration of time (months) in precontemplation and contemplation stages for a 60 year old woman with specified race and study group

	Precontemplation		Contemplation
	White	Non-white	White	Non-white
Control	42	59	15	22
Intervention	35	49	13	18

An assumption of this analysis was the use of the Markov property and stationarity. The stationary property assumes that the movement of subjects from one state to another is independent of time or in other words, has a constant transition probability matrix. This assumption of a constant transition matrix allows for us to determine the probability of movement and then the determination of the length of stay. Some researchers have examined the order of the dependence [10]. This technique has very low power unless there are numerous time points (more than 30). Therefore, similar to Perez, Chan, and others [16], we used a split-sample validation method to address the appropriateness of the model assumption. The Project HOME data was randomly split into developmental (or expected count, n = 1273) and validation (observed counts, n = 1273) datasets, stratified by Intervention/Control, White/Non-white, and two Age categories. A chi-square test with a null hypothesis; the Markov chain model from the developmental dataset fits the validation dataset. A comparison of the expected length of stay in the developmental dataset to the observed length of stay from the validation dataset produced a test statistic of 2.546 which was not significant at the 0.05 level.

4. Conclusions

This study has shown that continuous-time Markov models can be applied to population-based randomized group intervention trials with three-state categorical outcomes and that the inclusion of covariates allows for more precise probabilities tailored to individual subgroups. Overall, Markov processes are useful in characterizing transition rates between states. In this analysis, the relationship between a trinomial longitudinal outcome and three covariates was examined, with the primary assumption being that the within-subject changes of the outcome variable follow a continuous-time Markov model. An empirical study was conducted to evaluate the estimators and then the technique was demonstrated with the Project HOME data. In the analysis of the Project HOME data, the Markov technique which permitted the analysis of the three-category stage of change construct provided a clearer understanding of the stage transition and of the influence on subgroups that could be useful in developing future interventions. For example, precontemplators on average spend more time during the study period in their stage than contemplators but, surprisingly Project HOME participants in the precontemplation stage were more likely to progress to action than contemplation. Furthermore, average-age white intervention subjects spend less time in precontemplation and contemplation than average-age white control subjects. These effects could be due to an increase in mammography screening knowledge, lessened perceived risk, or other variables addressed by the intervention.

One drawback of the Markov model is its lack of acknowledgement of the ordinal structure of responses. Yet, at the intervention development stage of research what is important is not the idea of placement in a better or worse state but the determination of what state subjects are in and where and why they have transitioned to another. This information is important in order to better serve the larger population. Another possible limitation of this technique is its applicability to only three-state outcomes, but its use of more than one simultaneous covariate is very beneficial. Therefore, the next step in this research is to derive the likelihood equation for outcomes with n-states and possibly extending the model to include separate regression coefficients.

This Markov technique, although complex, provides information that is currently impossible to attain from traditional longitudinal methods such as generalized estimating equations that describe population behavior, or generalized linear mixed models, a subject-specific approach that provides the probability of movement but not an ability to examine the relationship between movement and time. Also, this technique may provide information when current Markov modeling statistical software fails to converge. The lack of information with regards to the relationship between time and movement provides a unique placement in longitudinal methods for continuous-time Markov Chains. This model can be used by researchers to more fully describe transitions in the data.