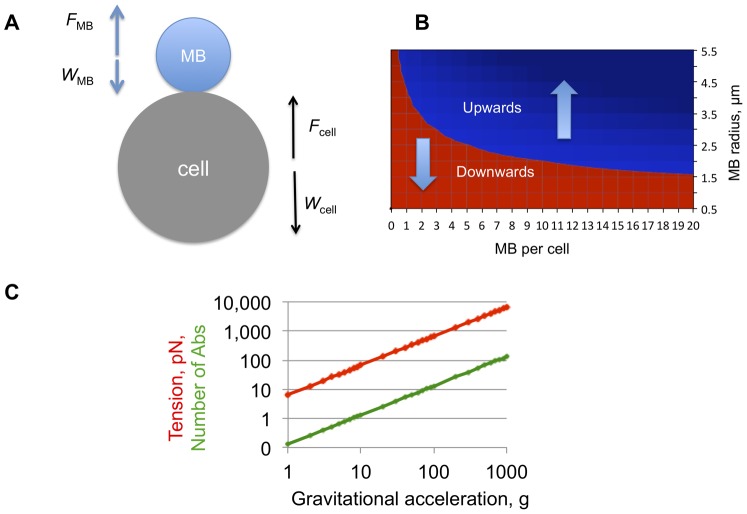
Figure 3. Theoretical feasibility of cell flotation after MB attachment.

The number of MBs to pull up a cell and the force acting on the MB-cell attachment was calculated based on the buoyancy law as described in Methods. A, In a non-viscous aqueous medium, cells and MBs experience the buoyant force (F) and the gravitation force or weight (W). Tension (force acting to disrupt MB–cell attachment) is the sum of F and W. This scheme does not take into account the forces acting in blood, such as drag (viscous resistance) and cell-cell interactions; B, Phase diagram showing the balance of gravity and buoyant forces at different MB sizes and MB/cell ratios. Cell diameter of 20 µm was used for the calculations. In the red zone, the weight of MB-cell complexes prevails and the complexes sediment; in the blue zone the buoyancy takes over and the complexes float. Gravitational acceleration does not affect the direction of the MB-cell complexes but only increases the speed of movement and tension force; C, Tension between a single 9 µm-diameter MBs and a 20 µm cancer cell as a function of g-force. Red line is the tension force; green line is the calculated number of antibodies required for holding a MB and a cell together (assuming that the force to pull out a phospholipid from the membrane is equal to 50 pN [29], [30], [31]).