Update on Grand Challenge Competition to Predict in Vivo Knee Loads

Short abstract

Validation is critical if clinicians are to use musculoskeletal models to optimize treatment of individual patients with a variety of musculoskeletal disorders. This paper provides an update on the annual Grand Challenge Competition to Predict in Vivo Knee Loads, a unique opportunity for direct validation of knee contact forces and indirect validation of knee muscle forces predicted by musculoskeletal models. Three competitions (2010, 2011, and 2012) have been held at the annual American Society of Mechanical Engineers Summer Bioengineering Conference, and two more competitions are planned for the 2013 and 2014 conferences. Each year of the competition, a comprehensive data set collected from a single subject implanted with a force-measuring knee replacement is released. Competitors predict medial and lateral knee contact forces for two gait trials without knowledge of the experimental knee contact force measurements. Predictions are evaluated by calculating root-mean-square (RMS) errors and R² values relative to the experimentally measured medial and lateral contact forces. For the first three years of the competition, competitors used a variety of methods to predict knee contact and muscle forces, including static and dynamic optimization, EMG-driven models, and parametric numerical models. Overall, errors in predicted contact forces were comparable across years, with average RMS errors for the four competition winners ranging from 229 N to 312 N for medial contact force and from 238 N to 326 N for lateral contact force. Competitors generally predicted variations in medial contact force (highest R²= 0.91) better than variations in lateral contact force (highest R²= 0.70). Thus, significant room for improvement exists in the remaining two competitions. The entire musculoskeletal modeling community is encouraged to use the competition data and models for their own model validation efforts.

Introduction

Musculoskeletal models can facilitate the design of surgical and rehabilitation treatments for a variety of patient populations with musculoskeletal disorders. The use of models in treatment planning provides an objective method for predicting the optimal treatment for a specific patient and allows clinicians to explore a variety of treatment options without added expense or risk to the patient. However, validation of musculoskeletal models by comparing model predictions to experimental measurements is a significant challenge that must be overcome before models can be widely accepted for use in a clinical setting [1].

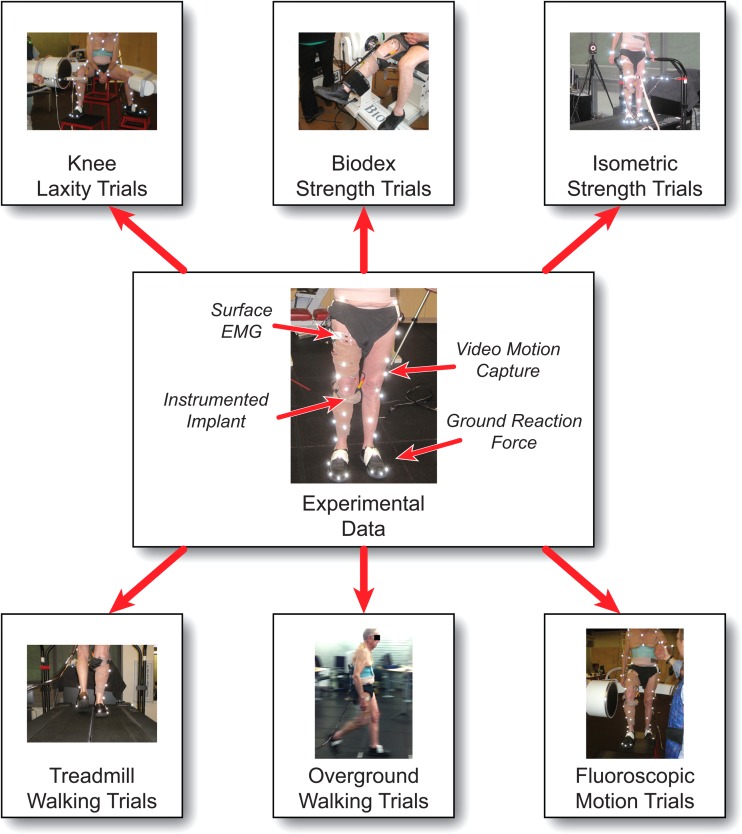
The Grand Challenge Competition to Predict in Vivo Knee Loads [2] was motivated by the need for an unbiased and thorough evaluation of musculoskeletal model predictions of contact and muscle forces in the knee. The competition has been held in 2010, 2011, and 2012 at the annual American Society of Mechanical Engineers Summer Bioengineering Conference, with two more competitions planned for the 2013 and 2014 conferences. Each year, the competition organizers release a comprehensive data set collected from a single subject implanted with a force-measuring knee replacement [3,4]. These data include motion capture marker trajectories (from a modified Cleveland Clinic marker set with additional markers on the feet and trunk), ground reaction forces and moments, electromyographic signals, dynamometer measurements, medial and lateral knee contact forces, and fluoroscopic, CT, and MR images (Fig. 1). The internal knee contact force measurements provide a means for validating musculoskeletal model predictions of knee contact forces directly and knee muscle forces indirectly. Here we present the contact force predictions from the winners [5–8] of the first three competitions (2010, 2011, and 2012), discuss the different modeling methods used by competitors, and summarize lessons learned from the competition thus far.

Fig. 1.

Overview of the experimental data available for past and future Grand Challenge Competitions. Four types of experimental data (shown in the center) are available for the six main categories of data collected (shown at the top and bottom).

Methods

For each competition, competitors are asked to predict medial and lateral knee contact forces for two gait trials without knowledge of the experimental contact force measurements. The competition gait trials are selected from a variety of gait modifications performed by the subjects (Table 1). Competition gait trials are selected such that the measured contact forces are in some way unique or unexpected (e.g., high medial contact force for a gait modification expected to produce low medial contact force or widely varying contact forces for two trials of the same gait modification). For the first two competitions (2010 and 2011), competitors were asked to predict contact forces measured from two different subjects during two trials of trunk sway gait, where subjects were instructed to increase medial-lateral sway of the trunk during walking (Table 1) [9]. For the third competition (2012), competitors were asked to predict contact forces during one trial of normal gait and one trial of medial thrust gait, where the subject was instructed to medialize the knees during stance phase to reduce medial contact force (Table 1) [10]. For all three competitions, competitors were asked to generate blinded contact forces predictions (i.e., no knowledge of experimental measurements). For the third competition (2012), competitors were also asked to generate unblinded predictions with improved models after the experimental measurements were released to them. Knowledge of model changes needed to improve contact force predictions could elucidate where effort should be focused to improve modeling methods.

Table 1.

Descriptions of gait modifications that were performed by the subjects in past and future Grand Challenge Competitions. Note that not all gait modifications are available for each competition's data set.

Gait modification	Verbal instructions
Bouncy	Increased superior-inferior translation of the pelvis during the gait cycle.
Forefoot Strike	Striking the ground with the forefoot rather than the heel at initial contact.
Medial Thrust	Internally rotated hip of the stance leg so that the knees were medialized during stance. The subject was instructed not to increase knee flexion during stance.
Mild Crouch	Crouched position with a mild increase in knee flexion angle.
Moderate Crouch	Crouched position with a moderate increase in knee flexion angle.
Smooth	Reduced superior-inferior translation of the pelvis during the gait cycle.
Trunk Sway	Increased medial-lateral sway of the trunk during the gait cycle.
Walking Pole	Walking with hiking poles. The subject was instructed to place the tip of the ipsilateral pole on the ground opposite the contralateral heel at the instant of heel strike.
Long Poles	Hiking pole length corresponded to the length recommended by the manufacturer, where in a standing position the elbow is at a 90 degree angle when the pole is vertical with the tip on the ground.
Short Poles	Hiking pole length was 10% shorter than the manufacturer's recommendations.
Normal Width	Hiking poles placed on ground at self-selected width.
Wide Width	Hiking poles placed on ground as far laterally as comfortable.

Results

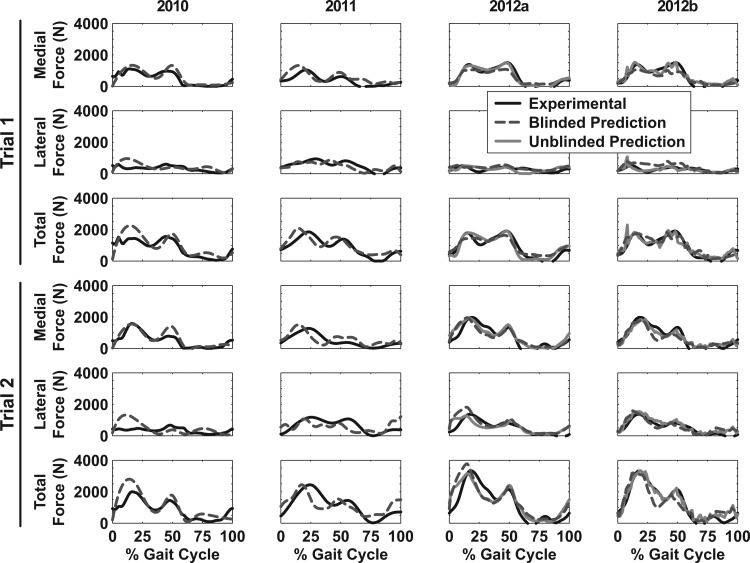
Eleven teams from nine countries participated in the first three competitions (2010, 2011, and 2012). Medial, lateral, and total contact forces measured experimentally and predicted by each winning team are shown in Fig. 2. Corresponding RMS errors and R² values are presented in Table 2. Note that in 2012, the competition judges selected two co-winners, and thus results are presented for two teams. Errors in contact force predictions are generally comparable across the three years of the competition (Table 2, Fig. 2).

Fig. 2.

Medial, lateral, and total contact forces over the gait cycle for the two trials selected for each competition. Experimental forces were measured with a force-measuring knee replacement (black solid line) and predicted by the 2010 [5], 2011 [6], and 2012 [7,8] winners of the competition. In 2010 and 2011, competitors were asked to submit only blinded predictions (dark gray dashed line). In 2012, competitors were asked to submit blinded (dark gray dashed line) and unblinded (light gray solid line) predictions, and the judges selected two co-winners (2012a and 2012b).

Table 2.

Root-mean-square errors (RMSE) and R² values for medial, lateral, and total contact forces over the gait cycle for the two trials selected for each competition. Calculations compare contact force predictions submitted by competitors with experimentally measured contact forces. Average RMSE and R² values for both trials are also presented. In 2012, competitors were asked to submit both blinded and unblinded predictions, and the judges selected two co-winners (2012a and 2012b). The lowest RMSE and highest R² values for medial, lateral, and total contact force are highlighted in bold text for the blinded predictions for each trial and the average.

			2010 [5] (Blinded)	2011 [6] (Blinded)	2012a [7] (Blinded)	2012a [7] (Unblinded)	2012b [8] (Blinded)	2012b [8] (Unblinded)
Trial 1	Medial Force (N)	RMSE	213	293	237	130	285	216
	R2	0.82	0.58	0.91	0.95	0.87	0.88
	Lateral Force (N)	RMSE	259	217	144	173	243	112
	R2	0.10	0.47	0.44	0.03	0.46	0.45
	Total Force (N)	RMSE	404	335	268	262	262	275
R2	0.70	0.69	0.89	0.84	0.85	0.82
Trial 2	Medial Force (N)	RMSE	246	330	351	291	330	242
	R2	0.81	0.43	0.73	0.83	0.80	0.91
	Lateral Force (N)	RMSE	393	384	332	288	241	198
	R2	0.05	0.14	0.66	0.54	0.70	0.88
	Total Force (N)	RMSE	477	530	608	529	483	285
R2	0.76	0.45	0.73	0.77	0.80	0.94
Average	Medial Force (N)	RMSE	229	312	294	210	308	229
	R2	0.82	0.50	0.82	0.89	0.83	0.89
	LateralForce (N)	RMSE	326	301	238	231	242	155
	R2	0.08	0.30	0.55	0.29	0.58	0.66
	Total Force (N)	RMSE	440	432	438	395	372	280
R2	0.73	0.57	0.81	0.81	0.82	0.88

Discussion

In the first three years of the competition, competitors used a variety of musculoskeletal modeling methods to predict contact and muscle forces. These methods include static and dynamic optimization, EMG-driven models, and parametric numerical models. Competitors who used optimization employed methods that are generally accepted for reducing the redundancy present in the musculoskeletal system, including minimizing activation and muscle stress. Other competitors used numerical models with physiological constraints, including minimizing muscle stress.

Only five of the eleven competitors (including Kim et al. [5] and Hast and Piazza [6], the winners from 2010 and 2011, respectively) used a deformable contact model (i.e., finite element or elastic foundation) to predict medial and lateral contact forces, while the remaining six competitors used simpler methods (e.g., splitting the load proportionally between compartments or using force or moment balancing). Details of the muscle and contact force modeling methods developed by Hast and Piazza [6] are presented in a subsequent paper in this special issue. Comparisons between the four winners (Table 2) show that while the winners in 2010 [5] and 2011 [6] used a contact model to predict contact forces, the results from the winners in 2012 [7,8] without contact models had some of the lowest RMS errors and highest R² values. Thus, use of a contact model is not guaranteed to produce accurate predictions of contact forces, as other modeling assumptions and choices may have a greater influence on model accuracy.

Ligament models were included by six of the eleven competitors. However, it is unclear to what extent the competitors calibrated the ligament parameters to the specific subject or if the ligaments contributed significantly to knee contact forces. To our knowledge, none of the competitors have investigated the influence of ligament parameters on the prediction of medial and lateral contact forces during gait. Thus, subject-specific ligament modeling remains an important area of research that may play a role in future Grand Challenge Competitions.

The results of the Grand Challenge Competition thus far have revealed interesting trends in the model predictions. In general, competitors have higher accuracy when predicting medial contact force compared to lateral contact force. Competitors were able to predict medial contact force blindly with R² values as high as 0.91 (2012a Blinded [7], Table 2, Trial 1) compared to lateral contact force predictions where R² values peaked at 0.70 (2012b Blinded [8], Table 2, Trial 2). Several competitors have observed that muscle and contact force predictions are sensitive to knee joint kinematics. Therefore, accurate measurement of knee kinematics appears to be an important issue in obtaining medial and lateral contact force predictions that closely agree with experimental measurements.

Completely different modeling methods have been able to produce contact force predictions of comparable accuracy, as demonstrated by the two co-winners in 2012 (Table 2, Fig. 2). Manal and Buchanan (2012a) used an EMG-driven musculoskeletal model to predict muscle and contact forces [7]. In contrast, Knowlton et al. (2012b) used a parametric numerical model to predict a space of feasible solutions for medial and lateral contact forces [8]. These two teams present the details of their methods and results in two subsequent papers in this special issue.

Two years of the Grand Challenge Competition remain, providing the musculoskeletal modeling community with additional opportunities to improve existing modeling methods or develop new ones with better accuracy. Data from the Grand Challenge Competitions are available on the competition website.1 Our hope is that the musculoskeletal modeling community will use the data not only for participation in the Grand Challenge Competition but also for their own research, publication, and grant proposal efforts.