Familial cosegregation of rare genetic variants with disease in complex disorders

Abstract

Family-based designs are increasingly being used for identification of rare variants in complex disorders. This paper addresses two questions related to the utility of these designs. First, under what circumstances are rare disease-related variants expected to cosegregate with disease in families? Second, under what circumstances is a disease–variant association expected to be greater in studies restricted to familial cases than in studies of unselected cases? To investigate these questions, we developed a probability model of disease causation involving two loci. To address cosegregation, we examined the probability that an affected first-degree relative of a variant-carrying proband would also carry the variant. We find that this probability increases with increasing odds ratio (OR) for the variant, but declines with increasing sibling recurrence risk ratio (λ_s). For example, under reasonable assumptions, the 15q13.3 microdeletion in idiopathic generalized epilepsy, with an OR estimate of 68 in large case–control studies, is expected to be present in >95% of affected first-degree relatives of variant-carrying probands. However, for a variant with OR=5, the probability an affected relative has the variant ranges from 82% (when λ_s=2) to 58% (when λ_s=50). We also find that restriction of a study to familial cases does not necessarily increase a rare variant's association with disease, especially if λ_s is high and the variant contributes little to overall disease familial aggregation. These findings provide guidance for the design of family-based studies of rare variants in complex disorders.

Introduction

The genetic architecture of human disease includes a spectrum ranging from rare monogenic variants with very strong effects to common variants with small effects on the disease phenotype. Variants in the upper end of this spectrum have traditionally been investigated through linkage analysis in rare Mendelian families, whereas those at the opposite end have been investigated in genome-wide association studies (GWAS). The effect sizes of variants uncovered in GWAS have usually been very small, making it increasingly evident that a substantial proportion of the heritability of common diseases remains unexplained.¹ New molecular analysis methods such as massively parallel sequencing are likely to uncover a plethora of variants located between these extremes, that is, rare genetic variants with modest to high effect sizes. Although little is known about these variants, recurrent microdeletions recently discovered in neurodevelopmental disorders allow for a first insight into their properties, both in case–control and family studies.

Here, we address two questions related to the utility of family-based designs for the identification of rare variants in complex disorders. First, under what circumstances are rare disease-related variants expected to cosegregate with disease in families containing multiple affected individuals? Second, under what circumstances is the association of a variant with disease expected to be greater in affected individuals with an affected sibling than in unselected affected individuals?

We use as an example the relationship of the 15q13.3 microdeletion to idiopathic generalized epilepsy (IGE). The 15q13.3 microdeletion is implicated in several neurodevelopmental or neuropsychiatric disorders, including intellectual disability, autism, schizophrenia, and IGE.^{2, 3, 4, 5} In contrast to many other neurodevelopmental disorders, IGE is a distinct but relatively mild phenotype with a substantially increased familial risk (approximately eightfold in siblings of affected individuals⁶). The 15q13.3 microdeletion appears to confer a higher risk for IGE than for other neurodevelopmental disorders,⁷ and a current estimate of the odds ratio (OR) for this variant in individuals with IGE compared with unaffected individuals is 68 (95% confidence interval 29–181).⁸ Given this very high OR, evaluation of the effect of the 15q13.3 microdeletion in the families of deletion carriers is of interest.^{2, 8, 9} However, some previous studies of the families of IGE probands with the 15q13.3 microdeletion have had results that appear counterintuitive: despite the high OR from case–control studies, this variant did not appear to segregate consistently with disease in families.^{4, 8, 10} In the families of probands with the variant, some unaffected relatives have been found to carry the variant, a result easily explained by reduced penetrance. However, the variant has also been found to be absent in relatives who were affected, which is much more difficult to explain. This phenomenon has also been noted in the past, for example, in multiplex families with intellectual disability.¹¹ The findings have led some authors to conclude that in general, rare variants that contribute to risk for epilepsies with complex inheritance should not be expected to segregate with disease in families.^{8, 12}

We attempted to reconcile these findings by determining the conditions under which familial cosegregation of a rare variant with disease is expected. To address this problem, we developed a probability model based on simple assumptions about the factors other than the rare variant that influence disease risk in the families of affected probands who carry the variant. Our model assumes that disease risk is entirely attributed to the effects of two genetic loci, one of which is the rare variant under consideration. We operationalized the concept of familial cosegregation by considering the probability that the variant is present in an affected sibling of a variant-carrying proband. We estimated this probability under our model, based on the variant's frequency in the general population and in affected individuals (used to compute the OR), disease frequency, and sibling recurrence risk of the disease. We then used the same model to estimate the OR for the variant that would be expected in a study of affected individuals with affected siblings (ie, OR_fhx, defined below) and compared it with the usual OR (without subscript) in a study of unselected affected individuals.

Materials and methods

Parameter definitions

P(D=1) denotes the frequency of the disease in the general population, which is estimated to be 0.005 for IGE, based on an estimated 3% lifetime risk of all epilepsy,¹³ ∼15–20% of which is IGE.¹⁴

P(G=1) denotes the frequency of the variant (in heterozygous or homozygous state) in the general population. For the 15q13.3 microdeletion P(G=1) has been estimated to be 0.0002 in the Icelandic population,^{3, 5, 15} but might be lower in other European populations.⁸ For our estimates, we assume a frequency of 0.0002.

P(G=1|D=1) is the frequency of the variant in cases, that is, the probability of the variant given that an individual is affected. 15q13.3 microdeletions have been identified in ∼1% of patients with IGE, so that P(G=1|D=1)=0.01. This frequency is probably significantly higher than in other neuropsychiatric disorders.

The OR for the variant, estimated from case–control data, is

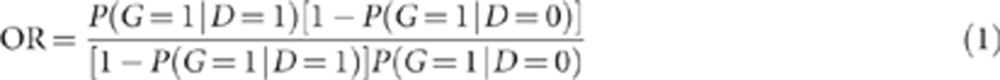As noted above, for the 15q13.3 microdeletion in IGE, the OR has been estimated as 68.⁸

P(D=1|G=1) refers to the penetrance of the variant, that is, the probability that an individual is affected given that he/she is a carrier of the variant. P(D=1|G=1) can be derived from the above parameters according to Bayes' theorem:

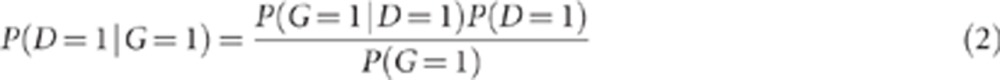In the example of the 15q13.3 microdeletion, penetrance=0.01 × 0.005/0.0002=0.25.

Probability that the variant is present in an affected sibling of a variant-carrying proband

For calculations pertaining to familial risk, we use subscripts s and p to refer to the disease and variant frequencies in a sibling or proband, respectively. Hence, the recurrence risk in the sibling of an affected proband is P(D_s=1|D_p=1), and λ_s, the sibling recurrence risk ratio,¹⁶ is P(D_s=1|D_p=1)/P(D_p=1). For probands with IGE, λ_s has been estimated as 8.4 when only siblings with IGE are considered,⁶ and 3–5 when siblings with any type of epilepsy are considered.^{6, 17, 18} As our analyses are based on an assumed population risk of IGE specifically (rather than of all epilepsy), we assume λ_s=8. This corresponds to a sibling recurrence risk of IGE of ∼4%.

Using the notation above, the probability that a specific variant under consideration is present in an affected sibling of a variant-carrying proband is P(G_s=1|D_s=1, G_p=1, D_p=1), and from the definition of conditional probability:

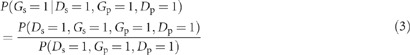To solve equation (3), we need to make some assumptions about the factors other than the genotype at the G locus that influence disease risk in the sibling of a proband who carries the variant. To model these factors, we assume disease risk involves two loci, G and H, where G is the locus under consideration so far, and H is another, unlinked and unknown gene. We assume each locus has two alleles in Hardy–Weinberg equilibrium, the two loci are not in linkage disequilibrium, and each locus is dominant with respect to disease risk. We allow for reduced penetrance of the susceptible genotypes (GG or Gg, and HH or Hh) but assume zero penetrance in the normal homozygote. We further assume that these two loci account for all of the disease risk in the population; that is, disease risk is 0 in individuals with the low-risk genotypes at both loci. The penetrance matrix for the two loci is shown in Table 1A.

Table 1. Two-locus penetrance matrix for genotypes G and H.

	G=1 (high-risk genotype at G locus (GG or Gg))	G=0 (low-risk genotype at G locus (gg))
(a) General definitions
H=1 (high-risk genotype at H locus (HH or Hh))	f1	f3
H=0 (low-risk genotype at H locus (hh))	f2	0
(b) Values under Risch's heterogeneity model1
H=1 (high-risk genotype at H locus (HH or Hh))	f1=1−(1−x1)(1−y1)	f3=1−(1−x0)(1−y1)
H=0 (low-risk genotype at H locus (hh))	f2=1−(1−x1)(1−y0)	0=1−(1−x0)(1−y0)

¹x₁, x₀, y₁, and y₀ are penetrance ‘summands' from Risch.¹⁶ Given our assumption of zero penetrance for individuals with G=0, H=0, these values imply: 1−f₁=(1−f₂)(1−f₃), leading to f₁=f₂+f₃−f₂f₃.

We let p=freq(GG or Gg genotype) and v=freq(G allele)=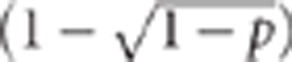. As the G locus in this example represents the 15q13.3 microdeletion, from our previous formulation this implies p=P(G=1)=0.0002 and v=0.0001. Similarly, we let q=f(HH or Hh genotype) and w=freq(H allele)=.

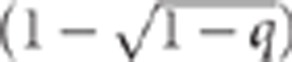As we are interested in genotype probabilities in proband-sibling pairs, we can simplify our calculations by recognizing that within each family, the alleles of the parents are transmitted independently to each successive offspring. Hence, we consider all of the possible parental ‘mating types' (ie, combinations of genotypes in mother and father) with regard to the G and H loci (Table 2). In our example, the G allele is very rare; hence we restrict attention to genetic parental mating types involving either 0 or 1 G allele (either gg × gg or Gg × gg). However, we consider all possible mating types at the H locus. Taking these genetic parental mating types into consideration, equation (3) can be written as:

Table 2. Components needed to compute probability that the variant is present in an affected sibling of a variant-carrying probanda.

Parental mating type at G and H loci	P(mating type)	P(D=1|mating type)b	P(D=1, G=1|mating type)c
Gg × gg, hh × hh	4v(1−v)3·(1−w)4	0.5f2	0.5f2
Gg × gg, hh × Hh	4v(1−v)3·4w(1−w)3	0.25 (f1+f2+f3)	0.25(f1+f2)
Gg × gg, hh × HH	4v(1−v)3· 2w2(1−w)2	0.5(f1+f3)	0.5f1
Gg × gg, Hh × Hh	4v(1−v)3·4w2(1-w)2	0.5(0.75f1+0.25f2+0.75f3)	0.5(0.75f1+0.25 f2)
Gg × gg, Hh × HH	4v(1-v)3·4w3(1-w)	0.5(f1+f3)	0.5f1
Gg × gg, HH × HH	4v(1-v)3·w4	0.5(f1+f3)	0.5f1
gg × gg, hh × hh	(1−v)4·(1−w)4	0	0
gg × gg, hh × Hh	(1−v)4·4w(1−w)3	0.5f3	0
gg × gg, hh × HH	(1−v)4·2w2(1−w)2	f3	0
gg × gg, Hh × Hh	(1−v)4·4w2(1−w)2	0.75f3	0
gg × gg, Hh × HH	(1−v)4·4w3(1−w)	f3	0
gg × gg, HH × HH	(1−v)4·w4	f3	0

^aAs the G allele is very rare, only mating types involving 0 or 1 G allele are considered.

^bP(D=1|mt)=f₁·P(G=1|mt) P(H=1|mt)+f₂·P(G=1|mt)·P(H=0|mt) + f₃·P(G=0|mt) P(H=1|mt).

^cP(D=1, G=1|mt)=f₁·P(G=1|mt) P(H=1|mt)+f₂·P(G=1|mt) P(H=0|mt).

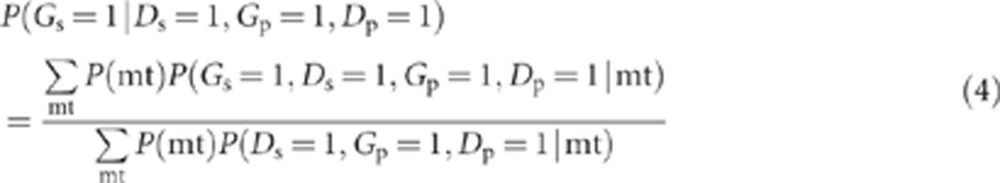where mt refers to the genetic mating type at the G and H loci. Within each parental mating type, each offspring (whether proband or sibling) is independent with regard to whether or not he/she inherits a high-risk genotype or develops disease. Thus, the term in the numerator of equation (4), P(G_s=1, D_s=1, G_p=1, D_p=1|mt), can be written as P(G_s=1, D_s=1|mt)·P(G_p=1, D_p=1|mt)=P((G=1, D=1|mt))² (ie, the subscripts that refer to proband and sibling can be removed). Similarly, the term in the denominator of equation (4), P(D_s=1, G_p=1, D_p=1|mt)=P(D_s=1|mt)·P(G_p=1, D_p=1|mt)=P(D=1|mt) P(G=1, D=1|mt). Hence,

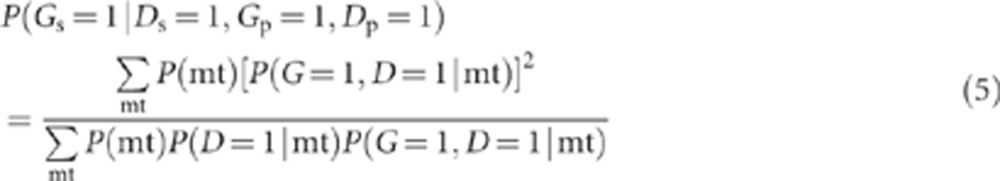where P(G=1, D=1|mt)=P(G=1, H=1, D=1|mt)+P(G=1, H=0, D=1|mt)

=P(D=1|G=1, H=1) P(G=1, H=1|mt)+P(D=1|G=1, H=0) P(G=1, H=0|mt)

= f₁· P(G=1|mt) P(H=1|mt)+f₂· P(G=1|mt) P(H=0|mt).

Similar reasoning yields P(D=1|mt)=

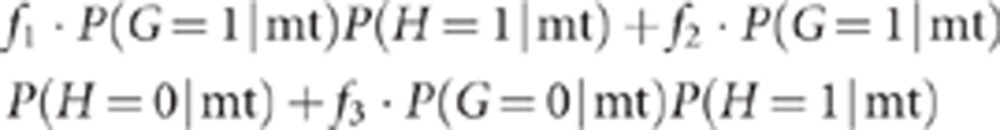Table 2 shows general formulae for all of the ‘components' needed to compute the individual terms in the summations in (5).

OR for the variant in affected individuals with an affected sibling

Under our model, the probability that the proband has the variant, given that he/she has an affected sibling, is

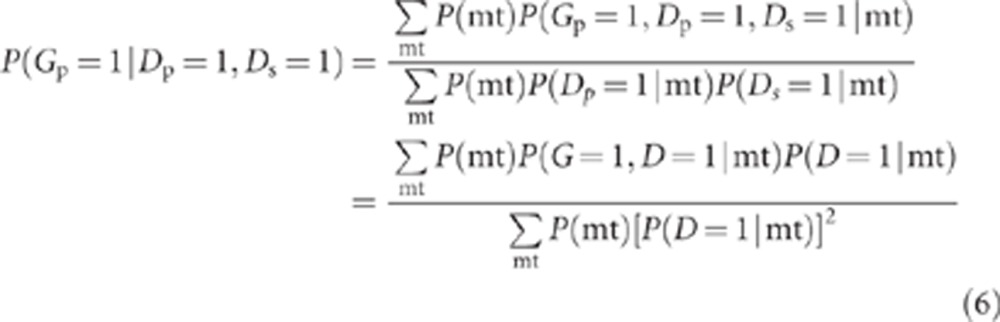where P(G=1, D=1|mt) and P(D=1|mt) are defined above. We define a new OR, OR_fhx, representing the odds of the variant in cases with an affected sibling vs unaffected controls.

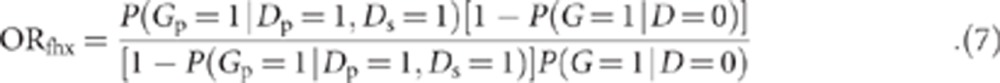We use the probability in equation (6) to derive a formula for this OR. Below, we use OR (without a subscript) to refer to the OR defined in equation (1) (ie, the OR in unselected cases vs controls), to distinguish it clearly from OR_fhx, defined in equation (7).

Finding a numerical solution consistent with the data

To estimate the probabilities in equations (5) and (7) under specific scenarios, we need to derive reasonable values for f₁, f₂, f₃, and q. To do this, we note that specific algebraic relationships hold, under the assumptions of the model in Table 1. First, the overall disease frequency is equal to:

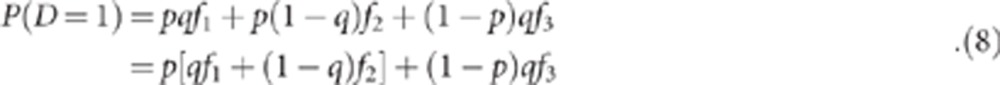The penetrance of the G genotype is equal to:

From equations (8) and (9), we obtain:

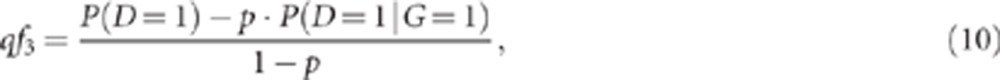which can be calculated from our input parameters.

If we can obtain a value for f₃, we can derive f₁ and f₂ using reasonable assumptions about the relations between G and H in terms of their effect on disease risk. For example, under Risch's heterogeneity model,¹⁶ f₁=f₂+f₃–f₂f₃ (Table 1, Part b), and substituting for f₁ in equation (9), we obtain:

For an alternative model, we assume a model of ‘epistasis' (in the sense that the combined effects of the G and H loci are greater than additive) in which f₁=1.0 (ie, all of the individuals with both G and H are affected). Under this model, P(D=1|G=1)=qf₁+(1q)f₂, and hence,

Second, we note, again, that conditional on mating type, disease occurs independently in the proband and sibling. Hence, the sibling recurrence risk can be expressed as:

To obtain a reasonable value for q, we set q equal to a range of values between qf₃ and 1, which in turn provides values for f₁, f₂, and f₃ under the model assumed in equations (11) or (12). Then, we use equation (13) to compute the corresponding sibling recurrence risk for each value of q, and select the value consistent with the observed sibling recurrence risk (see below).

Although the reasoning above is presented in terms of the probability that an affected sibling of a variant-carrying proband will carry the variant, we also performed the same modeling with regard to this probability for an affected offspring or parent. The results were exactly the same as those for an affected sibling; hence we conclude that for the model used here, the results apply to all first-degree relatives and not only siblings.

Results

Application to probability that an affected sibling has the 15q13.3 microdeletion

We first used the model described above to estimate the probability that an affected sibling of a proband with the 15q13.3 microdeletion would also carry this variant. To estimate f₁, f₂, f₃, and q for the 15q13.3 microdeletion and IGE, we consider the information we have: P=0.0002, P(D=1)=0.005, and P(D=1|G=1) (ie, the penetrance of the microdeletion)=0.25. Also, the sibling recurrence risk =0.04. In this example, equation (10) gives:

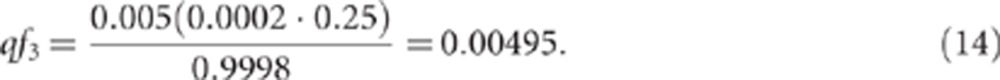Under the heterogeneity model in equation (11), this implies f₂=(0.25–0.00495)/(1–0.00495)=0.2463, and hence f₁=0.2463+0.00495/q−(0.2463·0.00495/q). This relationship constrains the value of q to be ≥0.00495 (ie, the value of qf₃ derived above); lower values of q would imply that f₁>1.0.

For the observed recurrence risk of 0.04 for IGE, we obtain an estimate of q=0.066, which leads to f₁=0.303, f₂=0.246 (as above), and f₃=0.075. Using these values in equation (5) leads to P(G_s=1|D_s=1, G_p=1, D_p=1)=97.9%.

If we assume the epistatic model in equation (12), we obtain q=0.066 (as before), f₁=1.0, f₂=0.197, f₃=0.075 (as before), and the probability that an affected sibling has the variant is slightly lower than before: 96.4%, but still very high.

Extension to other inheritance models

We also considered whether other genetic inheritance models could lead to a different outcome. Our analysis indicated that given our input data for the 15q13.3 microdeletion in IGE – that is, P(D=1)=0.005, P(G=1)=0.0002, P(D=1|G=1)=0.01, and sib recurrence risk=0.04 – the system is quite constrained. Specifically, the value of q is constrained to be very close to 0.066, and this in turn implies f₃ is very close to 0.075. Given these values, mating types involving both the rare 15q13.3 variant and other genetic causes (represented by locus H in our example) are extremely rare. In our example, almost all affected individuals who carry the variant come from mating type Gghh × gghh, so that the only way their siblings can develop disease is through the effects of G. We conclude that given the assumptions of our model and the input data for the 15q13.3 microdeletion in IGE, the probability that an affected sibling of a variant-carrying proband also carries the variant cannot deviate substantially from the two values reported above, and certainly seems unlikely ever to be <95%.

Relationship to OR and sibling recurrence risk ratio

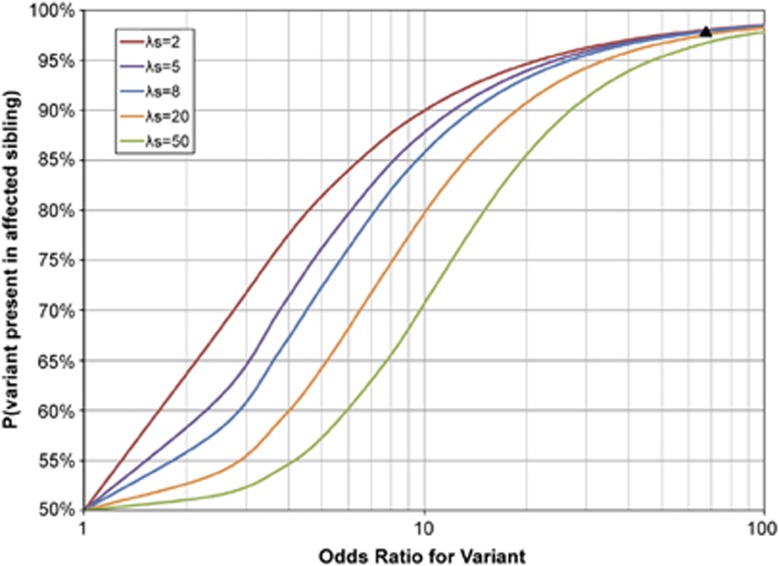
Figure 1 shows the probability the variant is present in an affected sibling of a variant-carrying proband under the heterogeneity model,¹⁶ as a function of the OR in equation (1) and sibling recurrence risk ratio, λ_s. Although the findings are presented for siblings, as noted above we have also determined that they also apply to other classes of first-degree relatives (affected offspring or parents of variant-carrying probands). For a given level of familial aggregation (λ_s), the probability that an affected sibling has the variant increases with increasing OR for the variant. Also, for a given OR, the probability that an affected sibling has the variant declines with increasing λ_s.

Figure 1.

The probability that a rare variant is present in an affected sibling of a variant-carrying proband, as a function of the OR and the sibling recurrence risk ratio, λ_s, where λ_s is the sibling recurrence risk divided by population disease frequency. Disease assumed to be caused by variants at two loci, G and H, with a penetrance matrix described by Risch's heterogeneity model¹⁶ as shown in Table 1b. Population disease frequency assumed to be 0.005 and variant frequency at G locus assumed to be 0.0002. The black triangle indicates the expected result for parameters corresponding to the 15q13.3 microdeletion in IGE.

The results in Figure 1 are based on an assumed disease frequency of 0.005 and variant frequency of 0.0002 in the general population, consistent with IGE and the 15q13.3 microdeletion. We evaluated the impact of these assumptions by changing the assumed disease frequency and variant frequency. Changing the disease frequency had virtually no impact on the findings. Increasing the variant frequency in the general population (so that the OR declined) led to a decrease in the probability that the affected sibling had the variant, equivalent to the trend shown in Figure 1.

For many of the other microdeletions implicated in neurodevelopmental disorders, ORs of 5–10 are observed. Although these ORs are substantially higher than those observed in most GWAS, they imply penetrance estimates of only 6–8%.⁷ Our results suggest that with ORs of this magnitude, under Risch's heterogeneity model¹⁶ anywhere from 65 to 90% of the affected siblings of a proband who carries the variant would also be expected to carry it (for λ_s ranging from 2 to 20, Figure 1). Hence, in some situations (particularly with low ORs and high λ_s), lack of clear cosegregation with disease in families is expected. An example of this is the pattern in four IGE families with inherited 15q11.2 microdeletions (OR of 4.9, λ_s≈8), where only three (43%) of seven tested affected first-degree relatives were found to carry the variant.⁹

The figure also reveals that at very low and very high ORs, the sibling recurrence risk ratio has little effect on the probability of interest. For example, for ORs between 1.0 and about 1.3, the probability remains between 50 and 55%, over the whole range of λ_s values considered there, and for ORs over 50, the probability is between 95 and 100% for all those λ_s values. In contrast, for ORs around 5, the probability ranges from 58% (when λ_s=50) to 82% (when λ_s=2). This suggests that for rare variants with ORs of around 5, the likelihood of familial cosegregation with disease is critically dependent on the overall level of familial aggregation.

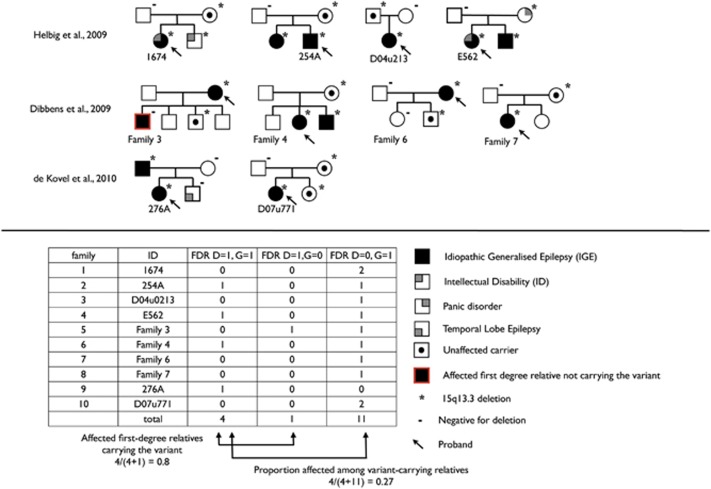
Comparing the theoretical predictions to existing data

To compare our theoretical predictions with existing data on the segregation pattern of the 15q13.3 microdeletion, we tabulated data from informative families with IGE, that is, families in which first-degree relatives were genotyped, clinical information was available, and the 15q13.3 microdeletion was identified in the proband and confirmed to be inherited as opposed to de novo.^{2, 8, 9} Information was available on 10 families that met these criteria (Figure 2). In these 10 families, 5 first-degree relatives were affected with IGE and four of them (80%) carried the variant. Conversely, the variant was present in 15 first-degree relatives, of whom 4 (27%) were affected with IGE. Three first-degree relatives with intellectual disability, panic disorder, or temporal lobe epilepsy who carried the variant were excluded from this analysis. The observed proportion of first-degree relatives with IGE who carried the variant was lower than expected (80% vs 97.9% expected, excluding de novo mutations). However, this is based on very small numbers (only five relatives); the exact P-value for the comparison is 0.101. Thus, from the available data on the 15q13.3 microdeletion, it would not be correct to conclude that familial cosegregation is not observed.

Figure 2.

Pedigrees of published IGE multiplex families with inherited 15q13.3 microdeletion.

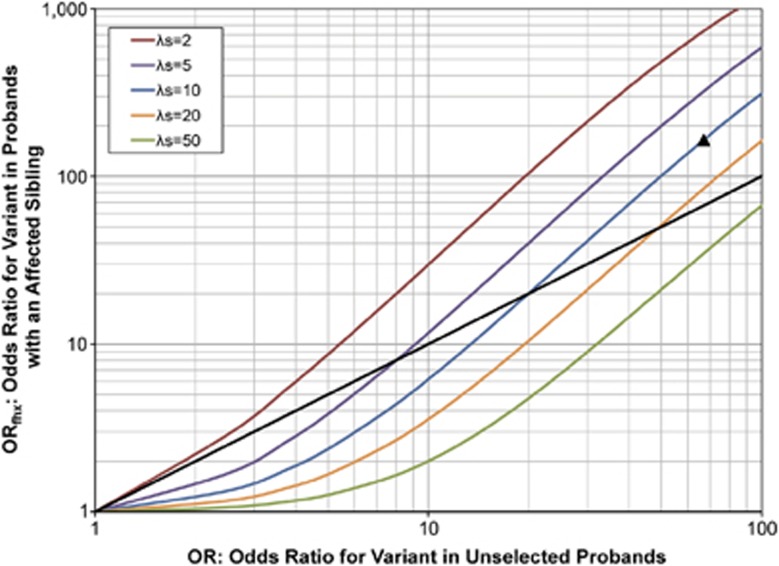
Impact of having an affected sibling on the OR of a rare variant: OR_fhxvs OR

Next, we investigated whether the OR_fhx is expected to be higher than the OR, that is, do we expect a stronger disease–variant association in a study restricted to probands with an affected sibling than in a study of unselected probands? The answer to this question would obviously influence the selection of familial vs sporadic cases for genetic studies. Contrary to our expectation, we found that the OR_fhx is not always higher than the OR (Figure 3). When the level of familial aggregation was relatively low (eg, λ_s=2), the OR_fhx was higher than the OR over the full range of ORs examined. For higher values of λ_s, however, under some conditions the OR_fhx was predicted to be lower than the OR. For example, our model predicts that if the OR=5, the OR_fhx is expected to increase to 9 in a study of a disease with λ_s=2, but to decrease to 2.8 in a study of a disease with λ_s=8.

Figure 3.

The expected OR for the variant in cases with an affected sibling vs unaffected controls (OR_fhx, y axis), and in unselected cases vs unaffected controls (OR, x axis). Disease assumed to be caused by variants at two loci, G and H, with a penetrance matrix described by Risch's heterogeneity model¹⁶ as shown in Table 1b. Population disease frequency assumed to be 0.005 and variant frequency at G locus assumed to be 0.0002. The dashed black line indicates equal OR_fhx and OR. The black triangle indicates the expected result for parameters corresponding to the 15q13.3 microdeletion in IGE.

Discussion

We developed a simple probability-based model to explore the expected behavior of rare variants in families containing multiple affected individuals. The results have important implications with regard to the utility of family-based designs for detecting these variants.

First, the magnitude of a variant's effect on disease risk (measured in terms of the OR) strongly predicts whether or not it cosegregates with disease in families. This suggests (consistent with¹⁹) that tests of cosegregation in family data will not be very useful for identifying variants of small effect. However, for variants with ORs of 30 or higher, cosegregation with disease in families is expected: almost all affected first-degree relatives of probands who carry the variant are also expected to carry it. Although the actual numbers we report in Figure 1 depend on the specific assumptions used in our model, we believe the qualitative conclusions will hold even if some of those assumptions are relaxed.

The results in Figure 1 also provide quantitative estimates of the magnitude of the OR that would lead an investigator to expect cosegregation. If case–control data indicate an OR greater than ∼30, but family data do not show cosegregation, the data are inconsistent. Either the OR is overestimated, for example, by ‘winner's curse' or an inappropriate control group, or the test of cosegregation is methodologically flawed, for example, by selection bias, phenotypic misclassification, or small sample size. In our example of the 15q13.3 microdeletion in IGE, some authors have concluded, based on the scanty data available, that the variant does not cosegregate. We demonstrate that the number of families studied is too small to provide a valid test.

Second, for variants with a modest effect on disease risk (OR 2–20), the overall level of familial aggregation influences the likelihood that an affected first-degree relative of a variant-carrying proband will also have the variant. If λ_s is high, variants with ORs in this range may be absent in a substantial proportion of the affected first-degree relatives of variant-carrying probands. For example, that proportion could be as high as one-third when the OR is 5 and the sibling recurrence risk ratio is as high as 20. This implies that in studies using next-generation sequencing, filtering strategies that restrict attention to variants shared by affected first-degree relatives may miss variants with a modest effect on disease risk, especially in highly familial disorders.

Third, the overall level of familial aggregation of the disorder is also an important consideration in decisions about whether or not to use familial samples for the detection of rare variants (Figure 3). When λ_s=2, the expected OR_fhx was higher than the usual OR, regardless of the OR in unselected cases. However, when the level of familial aggregation was higher (λ_s≥5), the OR_fhx in a study using familial cases was predicted to be lower than the OR in a study using unselected cases, unless the OR in unselected cases was very high. The explanation for this pattern is that when λ_s is relatively high, the rare variant contributes little to the overall disease familial aggregation, so that selection of familial cases leads to an increased likelihood that cases have other genetic causes of disease (represented by H in our model), and a reduced likelihood that they have the rare variant under consideration. These findings are similar to our previous results, which showed that study designs using cases with an affected sibling increase power to detect a rare variant when λ_s=2, but not when λ_s is higher.²⁰

The results in Figure 3 do not necessarily argue against the utility of study designs using samples of familial cases, however. They pertain to the OR (or OR_fhx) for a specific rare variant, whereas most studies aimed at gene discovery involve testing for an association with any of the variants involved, rather than with a single candidate variant. Our results do imply, however, that selection of cases with an affected sibling does not have the same effect on all of the genetic variants that contribute to risk. Instead, the use of familial cases selectively increases the frequency of the variants with the greatest contribution to disease familial aggregation. In fact, if familial aggregation resulted primarily from shared environmental factors, we would predict that a sample of cases with an affected sibling would have reduced frequencies of all of the genetic variants involved.

In the context of a Mendelian disorder, affected family members who do not carry the variant segregating in the family are considered ‘phenocopies.' Our findings show that such phenocopies are expected to be much more frequent for susceptibility variants that have ORs in the 5–10 range than for those with higher ORs. Hence, in complex disorders caused by variants with modest effects on disease risk, substantial genetic heterogeneity may be observed, even among closely related individuals within the same family. Application of new strategies for gene identification in complex disorders, such as massively parallel sequencing, need to take this heterogeneity into account.²¹

The authors declare no conflict of interest.