Our phantom analysis revealed that all commercial programs for CT perfusion and perfusion-weighted imaging studied showed delay-induced errors and/or insufficient correlations with true values, while all academic programs for perfusion-weighted imaging studied showed better correlations with true values.
Abstract
Purpose:
To design a digital phantom data set for computed tomography (CT) perfusion and perfusion-weighted imaging on the basis of the widely accepted tracer kinetic theory in which the true values of cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT), and tracer arrival delay are known and to evaluate the accuracy and reliability of postprocessing programs using this digital phantom.
Materials and Methods:
A phantom data set was created by generating concentration-time curves reflecting true values for CBF (2.5–87.5 mL/100 g per minute), CBV (1.0–5.0 mL/100 g), MTT (3.4–24 seconds), and tracer delays (0–3.0 seconds). These curves were embedded in human brain images. The data were analyzed by using 13 algorithms each for CT and magnetic resonance (MR), including five commercial vendors and five academic programs. Accuracy was assessed by using the Pearson correlation coefficient (r) for true values. Delay-, MTT-, or CBV-dependent errors and correlations between time to maximum of residue function (Tmax) were also evaluated.
Results:
In CT, CBV was generally well reproduced (r > 0.9 in 12 algorithms), but not CBF and MTT (r > 0.9 in seven and four algorithms, respectively). In MR, good correlation (r > 0.9) was observed in one-half of commercial programs, while all academic algorithms showed good correlations for all parameters. Most algorithms had delay-dependent errors, especially for commercial software, as well as CBV dependency for CBF or MTT calculation and MTT dependency for CBV calculation. Correlation was good in Tmax except for one algorithm.
Conclusion:
The digital phantom readily evaluated the accuracy and characteristics of the CT and MR perfusion analysis software. All commercial programs had delay-induced errors and/or insufficient correlations with true values, while academic programs for MR showed good correlations with true values.
© RSNA, 2012
Supplemental material: http://radiology.rsna.org/lookup/suppl/doi:10.1148/radiol.12112618/-/DC1
Introduction
Computed tomography (CT) perfusion is widely used for acute ischemic stroke (1–3), hemodynamic ischemia (4), subarachnoid hemorrhage (5), and brain tumors (6). Dynamic susceptibility contrast perfusion-weighted imaging also has been used in studies on acute ischemic stroke, such as the identification of ischemic penumbra (7,8) and the prediction of final infarction (9,10). Recently, a variety of postprocessing programs and algorithms for CT perfusion and perfusion-weighted imaging have been made available by CT and magnetic resonance (MR) imaging unit manufacturers, third-party workstation vendors, and academic groups. However, there are substantial differences between these programs and algorithms in terms of their maps and quantitative values in CT perfusion and perfusion-weighted imaging (11–14). It is difficult to determine the accuracy and reliability of each program, because precise implementations of analysis algorithms are generally not open to users, particularly in the case of commercial programs. Information about the type of algorithm, such as singular value decomposition (SVD) or maximum slope algorithm, is usually provided, but this information has little bearing on the correctness of its implementation and its accuracy. In addition, the accuracy and reliability of these programs have not been subject to standardized quality control. The importance of standardizing perfusion processing has recently been identified as a key factor in advancing stroke imaging (15).
The purpose of the present study was twofold: (a) to design a digital phantom data set for CT perfusion and perfusion-weighted imaging on the basis of the widely accepted tracer kinetic theory in which the true values of cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT), and tracer arrival delay are known and (b) to evaluate the accuracy and reliability of postprocessing programs by using this digital phantom.
Materials and Methods
Curve Generation for Digital Phantom
Concentration-time curves for the artery (arterial input function), vein (venous output function), and brain tissue were generated by using previously described methods (Appendix E1 [online]) (16,17).
Seven MTT values (3.4, 4.0, 4.8, 6.0, 8.0, 12.0, and 24.0 seconds) and five CBV values (1.0, 2.0, 3.0, 4.0, and 5.0 mL/100 g) were used for this curve simulation. The CBF values were determined from each pair of CBV and MTT values by using the central volume principle (CBF = CBV/MTT) (18). For example, CBF values were 2.5, 5.0, 7.5, 10.0, 12.5, 15.0, and 17.5 mL/100 g per minute when CBV was 1.0 mL/100 g, and CBF values were 12.5, 25.0, 37.5, 50.0, 62.5, 75.0, and 87.5 mL/100 g per minute when CBV was 5.0 mL/100 g. Seven increments of tracer delay (0, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 seconds) were achieved by shifting the concentration-time curve of tissue, or C(t), relative to the arterial input function. In total, 735 combinations of tissue curves were generated from three types of residue function (R[t]), seven values of MTT, five values of CBV, and seven delays.
Data Structure
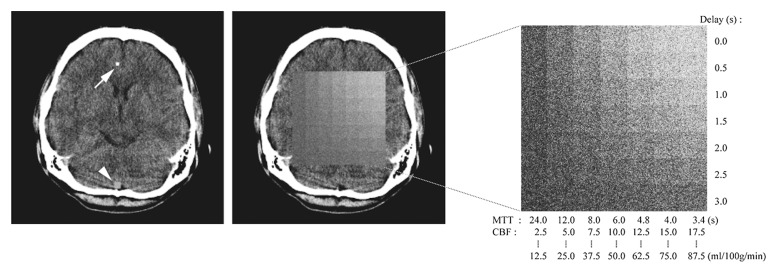
The digital phantom data set contained 16 section locations both for CT perfusion and perfusion-weighted imaging (Fig 1). Section 1 contained the arterial input function and venous output function, and tissue curves were embedded in sections 2–16. Matrixes of these sections were 512 × 512 for CT perfusion and 256 × 256 for perfusion-weighted imaging. Each tissue section contained 7 × 7 quadratic tiles. Each tile was encoded with increasing MTT (decreasing CBF) across columns (left to right) and increasing delays across rows. The data were exported to Digital Imaging and Communications in Medicine format, enabling import into all software packages used in the present study.
Figure 1a:
Data structure of digital phantom for CT. Digital phantom data consist of 16 sections (a). Image shows section (Slice) location. Section 1 (b, left) contains curves for arterial input function (arrow on b, left) and venous output function (arrowhead on b, left). Tissue curves are embedded in sections 2–16 (b, middle). The tissue section contains 7 × 7 quadratic tiles (b, right), which has a different delay and MTT. The first five sections (sections 2–6) have curves of exponential R(t), with each section having a particular value of CBV (1, 2, 3, 4, and 5 mL/100 g, respectively) (a). The next five sections (sections 7–11) and the final five sections (sections 12–16) have curves of linear R(t) and box-shaped R(t), respectively.
Figure 1b:
Data structure of digital phantom for CT. Digital phantom data consist of 16 sections (a). Image shows section (Slice) location. Section 1 (b, left) contains curves for arterial input function (arrow on b, left) and venous output function (arrowhead on b, left). Tissue curves are embedded in sections 2–16 (b, middle). The tissue section contains 7 × 7 quadratic tiles (b, right), which has a different delay and MTT. The first five sections (sections 2–6) have curves of exponential R(t), with each section having a particular value of CBV (1, 2, 3, 4, and 5 mL/100 g, respectively) (a). The next five sections (sections 7–11) and the final five sections (sections 12–16) have curves of linear R(t) and box-shaped R(t), respectively.
Data Analysis
The phantom data were postprocessed by using five commercially available software packages (GE Healthcare, Waukesha, Wis; Hitachi Medical Systems, Chiba, Japan; Philips Medical Systems, Best, the Netherlands; Siemens Healthcare, Erlangen, Germany; and Toshiba Medical Systems, Tokyo, Japan) and two academic programs (Perfusion Mismatch Analyzer [PMA], Acute Stroke Imaging Standardization Group [ASIST], Japan, http://asist.umin.jp/index-e.htm [11,12]; and Stroketool, Digital Image Solutions, Germany, http://www.digitalimagesolutions.de/) for CT perfusion (Table 1). Also used were four commercially available software packages (GE Healthcare, Hitachi Medical Systems, Philips Medical Systems, and Siemens Healthcare) and five academic programs, including Echoplanar Imaging Thrombolysis Evaluation Trial, or EPITHET (Melbourne Health, Melbourne, Australia) (19); perfusion graphical user interface, or Penguin (Danish National Research Foundation, Center of Functionally Integrative Neuroscience, Aarhus University, Aarhus, Denmark; http://www.cfin.au.dk/software/penguin); RAPID (Stanford University, Stanford, Calif) (20); PMA; and Stroketool (Digital Image Solutions) for perfusion-weighted imaging (Table 2). CBF, CBV, and MTT maps were generated by each package, except for the Echoplanar Imaging Thrombolysis Evaluation Trial program, which was limited to time to maximum of R(t) (Tmax) maps. All the academic programs for perfusion-weighted imaging also included generation of Tmax maps.
Table 1.
Software for CT Perfusion
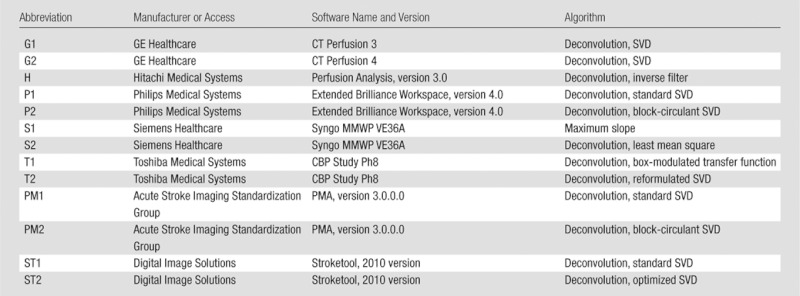
Table 2.
Software for Perfusion-weighted Imaging
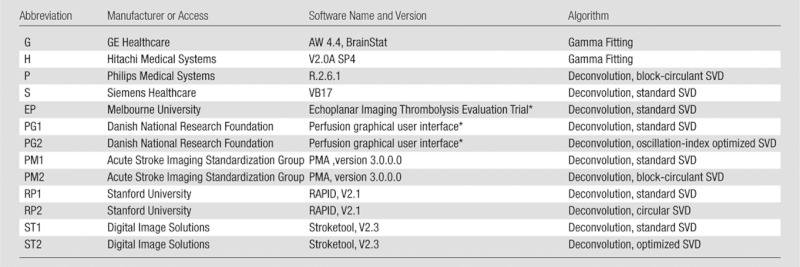
Information about the version was not available.
Region-of-interest measurements were automatically performed by using in-house software. The average pixel value for each of the 735 tiles was measured by using a square region of interest of 28 × 28 pixels in size for CT perfusion and one of 12 × 12 pixels in size for perfusion-weighted imaging (excluding the edge pixels, the pixel value of which might be affected by the surrounding pixels during smoothing procedures). To evaluate the accuracy of the software packages, the Pearson correlation coefficient r was calculated to determine correlation between each program’s results and the true values of CBF, CBV, and MTT. A good correlation was defined as one with r > 0.9. The slope and intercept of linear regression were also determined to evaluate the relationship between the values measured from each program and the true values. Differences among algorithms were tested by using one-way repeated-measures analysis of variance (ANOVA), and 95% confidence intervals for the slope and intercept were calculated. A two-way repeated-measures ANOVA was used to detect the bias of parameter estimates across the different true delay, CBV, and MTT values. To examine the delay-induced error in CBF, CBV, and MTT calculations for each program, delay was modeled as a main factor in the ANOVA. To examine the CBV dependency of CBF and MTT calculation, true CBV was modeled as a main factor in their calculation. Then, true MTT was used as a main factor for CBV calculation. Dependency on different R(t) values was also evaluated by using one-way ANOVA.
The Pearson correlation coefficient r was calculated for Tmax values for perfusion-weighted imaging between any pair of algorithms. A good correlation was defined as one with r > 0.9. The absolute values of Tmax were compared among the algorithms by using one-way repeated-measures ANOVA followed by a pairwise comparison with the Holm-Sidak test. The Pearson correlation coefficient r between Tmax and simulated delay or MTT was also calculated. The slope and intercept of linear regression were determined to evaluate the relationship between the Tmax values from each program and simulated delay or MTT.
A difference with a P value of less than .01 was treated as significant for all tests.
Results
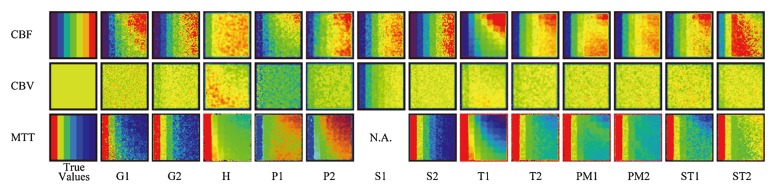
In CT perfusion, CBF maps (Fig 2a) showed delay-dependent variation for G1, P1, P2, T1, T2, PM1, ST1, and ST2 as a color gradient in the vertical direction; see Table 1 for an explanation of the abbreviations used here, in Figure 2a, and hereafter. In contrast, the color gradient was not clear in maps for G2, H, S1, S2, and PM2, which indicates delay insensitivity of these programs. Similarly, a delay-dependent vertical gradient was noted in MTT maps of G1, H, P1, P2, T1, T2, PM1, PM2, ST1, and ST2, whereas no vertical difference was observed in maps for G2 and S2. Delay-dependent vertical gradients were observed in CBV maps for H and T1. MTT dependencies were also noted in maps for G2, H, S1, T1, T2, and ST2 as a horizontal gradient.
Figure 2a:
Perfusion maps. True-value and perfusion maps of digital phantom (section 16, box-shaped R[t], and CBV [5 mL/100 g]) are shown with identical color lookup table (not shown). The color scale is automatically adjusted for visual assessment in each map of CBF, CBV, and MTT. A constant window level and window width (8 and 16 seconds, respectively) are used for Tmax. In the true-value maps of CBF and MTT, seven columns with different CBF or MTT show different colors. However, there is no vertical color gradient, because all seven rows have identical CBF or MTT and only the delay is different. The true-CBV image is uniform in color, because all 49 tiles have the same CBV value in a section. (a) CT perfusion. Delay-dependent vertical gradation is apparent in most of CBF (G1, P1, P2, T1, T2, PM1, ST1, and ST2) and MTT (G1, H, P1, P2, T1, T2, PM1, PM2, ST1, and ST2). In CBV, a delay-dependent vertical gradient is observed in H and T1. MTT dependency is also noted in G2, H, S1, T1, T2, and ST2 as a horizontal gradient. (b) Perfusion-weighted imaging. Delay dependency is apparent in most algorithms for CBF and MTT maps. Delay-dependent vertical gradient on CBV map is observed for P. MTT dependency is also noted for G, S1, and ST2 as a horizontal gradient. N.A. = not available.
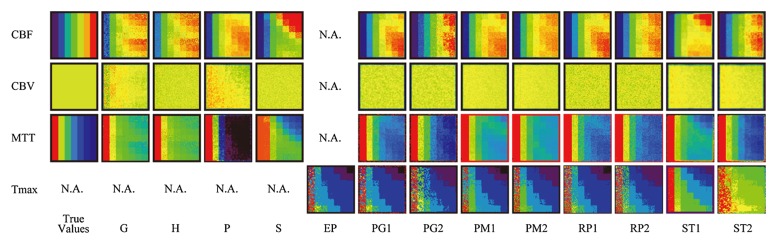
In perfusion-weighted imaging, CBF maps (Fig 2b) showed delay-dependent variation for G, H, P, S, PG1, PG2, PM1, RP1, and ST1, while maps for PM2, RP2, and ST2 did not show delay sensitivity; see Table 2 for an explanation of the abbreviations used here, in Figure 2b, and hereafter. Similarly, delay-dependency was clearly seen in MTT maps for S and ST1 and was observed to some extent in maps for G, H, PG1, PG2, PM1, PM2, RP1, and ST2. Delay-dependent vertical gradients in CBV maps for G and P were observed. MTT dependencies were also noted in maps for G, P, ST1, and ST2 as a horizontal gradient.
Figure 2b:
Perfusion maps. True-value and perfusion maps of digital phantom (section 16, box-shaped R[t], and CBV [5 mL/100 g]) are shown with identical color lookup table (not shown). The color scale is automatically adjusted for visual assessment in each map of CBF, CBV, and MTT. A constant window level and window width (8 and 16 seconds, respectively) are used for Tmax. In the true-value maps of CBF and MTT, seven columns with different CBF or MTT show different colors. However, there is no vertical color gradient, because all seven rows have identical CBF or MTT and only the delay is different. The true-CBV image is uniform in color, because all 49 tiles have the same CBV value in a section. (a) CT perfusion. Delay-dependent vertical gradation is apparent in most of CBF (G1, P1, P2, T1, T2, PM1, ST1, and ST2) and MTT (G1, H, P1, P2, T1, T2, PM1, PM2, ST1, and ST2). In CBV, a delay-dependent vertical gradient is observed in H and T1. MTT dependency is also noted in G2, H, S1, T1, T2, and ST2 as a horizontal gradient. (b) Perfusion-weighted imaging. Delay dependency is apparent in most algorithms for CBF and MTT maps. Delay-dependent vertical gradient on CBV map is observed for P. MTT dependency is also noted for G, S1, and ST2 as a horizontal gradient. N.A. = not available.
Correlation with True Values
In CT perfusion, a good correlation (r > 0.9) was achieved for CBF in seven of 13 algorithms (G1, P2, S1, T2, PM1, PM2, and ST1) (Table 3). Most programs showed a good correlation with true CBV, except for one algorithm (S1). Only four (H, T1, T2, and PM2) showed good correlation with true MTT. Only two (T2 and PM2) of 13 algorithms showed good correlation for all three parameters (ie, CBF, CBV, and MTT).
Table 3.
Correlation and Linear Regression with True Value for CT Perfusion
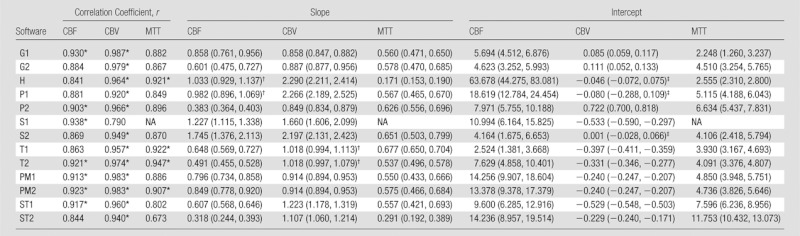
Note.—The software abbreviations are defined in Tables 1 and 2. Numbers in parentheses for slope and intercept are 95% confidence intervals. y = ax + b, x = true value, y = measured value, a = slope, b = intercept. NA = not available.
Values represent good correlations (r > 0.9).
The interval of the slope includes 1.0.
The interval of the intercept includes zero.
In perfusion-weighted imaging, all the academic programs showed a good correlation (r > 0.9) for CBF, CBV, and MTT (Table 4). In contrast, only two, three, and one of the four commercial programs showed a good correlation for CBF, CBV, and MTT, respectively.
Table 4.
Correlation and Linear Regression with True Value for Perfusion-weighted Imaging
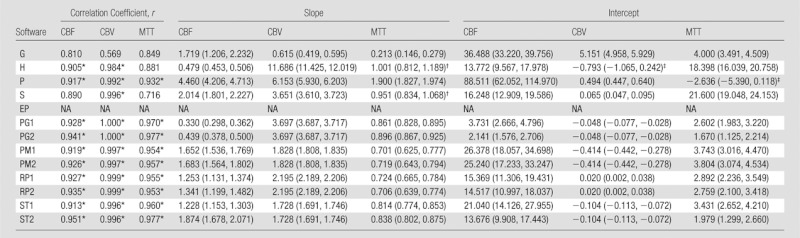
Note.—The software abbreviations are defined in Tables 1 and 2. Numbers in parentheses for slope and intercept are 95% confidence intervals. y = ax + b, x = true value, y = measured value, a = slope, b = intercept. NA = not available.
Values represent good correlations (r > 0.9).
The interval of the slope includes 1.0.
The interval of the intercept includes zero.
Ideally, the slope and intercept of linear regression with true values are expected to be 1.0 and zero, respectively. However, 95% confidence intervals of slope and intercept were away from 1.0 and zero in most of the algorithms, indicating that the absolute values calculated by using the programs were subject to scaling and offsetting errors (Tables 3, 4). In addition, these slopes and intervals significantly varied among the software packages according to ANOVA for all three parameters (CBF, CBV, and MTT) of both CT and MR.
Analysis of Error Sources
In CT perfusion, only four of 13 algorithms (H, S1, S2, and PM2) did not show significant delay dependency on CBF (Table 5). Most algorithms produced a CBF that depended on true CBV, except for two algorithms (H and P1). However, because of the interaction between delay and true CBV, program H was virtually dependent on both delay and true CBV, where delay dependency was observed with low CBV (1.0 mL/100 g), and CBV dependency was also noted with small amounts of delay (0, 1.0, and 1.5 seconds). The CBV of five algorithms showed delay dependency, whereas the remaining eight algorithms (G1, P1, P2, S1, S2, T2, PM1, and PM2) showed no delay dependency. On the other hand, all the algorithms showed significant CBV differences across the true MTT values, indicating that all the algorithms were susceptible to MTT differences on the basis of erroneous CBV calculation. For MTT, 11 were biased by delay and only two algorithms (S2 and PM2) were delay insensitive. However, both were dependent on CBV. Six algorithms (G2, H, P2, PM1, ST1, and ST2) also had true CBV dependency.
Table 5.
P Values of Repeated-measures ANOVA for CT Perfusion
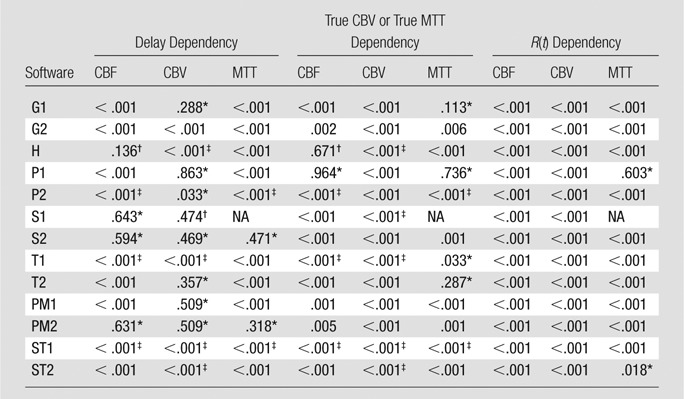
Note.—The software abbreviations are defined in Tables 1 and 2. For CBF and MTT, true CBV dependency is presented. For CBV, true MTT dependency is shown. NA = not available.
No significant dependency.
No significant dependency but significant interaction between delay and true CBV or true MTT.
Significant interaction between delay and true CBV or true MTT.
In perfusion-weighted imaging, 10 of 13 algorithms showed significant delay dependency for CBF (Table 6). Only two algorithms (PM2 and RP2) did not show any significant delay dependency. Most algorithms produced a CBF that depended on true CBV, except for one algorithm (PG1). CBV calculations in four algorithms showed delay dependency, whereas seven algorithms (H, PG1, PG2, PM1, PM2, RP1, and RP2) did not show any delay dependency. On the other hand, all the algorithms showed significant CBV differences across true MTT values, indicating that all the algorithms were susceptible to MTT differences on the basis of erroneous CBV calculation. For MTT, 10 algorithms were biased by delay and only two algorithms (PM2 and RP2) were delay insensitive.
Table 6.
P Values of Repeated-measures ANOVA for Perfusion-weighted Imaging
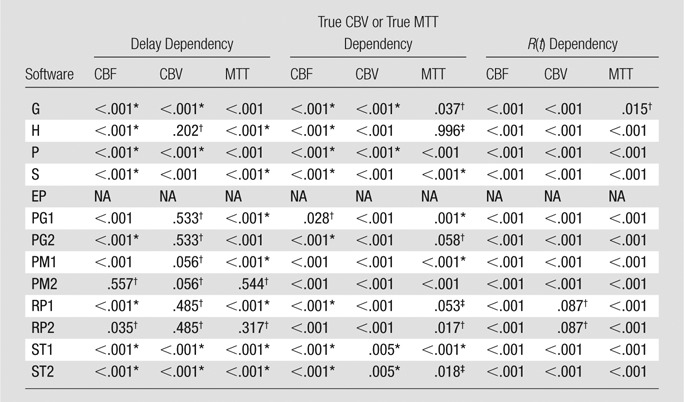
Note.—The software abbreviations are defined in Tables 1 and 2. For CBF and MTT, true CBV dependency is presented. For CBV, true MTT dependency is shown. NA = not available.
Significant interaction between delay and true CBV or true MTT.
No significant dependency.
No significant dependency but significant interaction between delay and true CBV and true MTT.
Significant dependencies on different types of R(t) were noted in almost all algorithms for both CT perfusion and perfusion-weighted imaging.
Correlation of Tmax for Perfusion-weighted Imaging
Almost all the pairs, except for one algorithm (ST1), showed good correlation for Tmax (r > 0.9) (Table 7). Absolute values of Tmax showed a significant difference with ANOVA, and a post hoc test showed that two algorithms (ST1 and ST2) showed significant differences from others. Correlations with delay or MTT and slopes of linear regression for delay or MTT were similar among all the algorithms, except for one algorithm (ST1). Intercepts for delay were also similar among most algorithms, except for two algorithms (ST1 and ST2); however, intercepts for MTT were more variable than delay among the algorithms.
Table 7.
Correlation and Linear Regression of Tmax Compared with Other Algorithms, Delay, or MTT
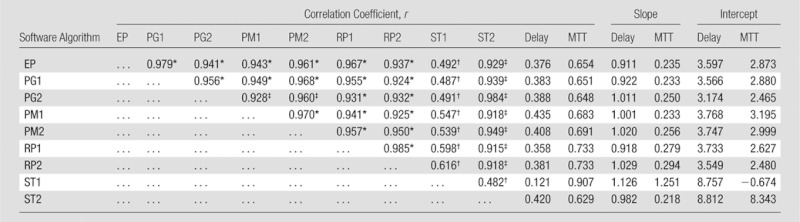
Value represents good correlations (r > 0.9).
Significant difference, determined with post hoc pairwise comparisons (Holm-Sidak test).
Significant difference, determined with post hoc pairwise comparisons (Holm-Sidak test), but the value represents good correlations (r > 0.9).
Discussion
In the current study, we demonstrated that the accuracy and reliability of an analysis program can be objectively assessed by using a digital phantom data set obtained on the basis of the widely accepted tracer kinetic theory in which true values of CBF, CBV, MTT, and tracer arrival delay are known. Delay-induced errors in CBF, CBV, and MTT are easily recognized visually. Statistical evaluation with region of interest measurements is also possible with the digital phantom, and the accuracy of the perfusion analysis can be determined by calculating correlations with true values, as well as error sources such as delay sensitivity and/or MTT or CBV dependencies.
In CT perfusion, only two algorithms (T2 and PM2) showed accurate results; however, algorithm T2 showed delay dependencies on CBF and MTT, and these can lead to potential errors in CBF and MTT calculations. In contrast, any delay dependencies were not shown in PM2, in which the circular type of SVD, developed as a delay-insensitive algorithm in perfusion-weighted imaging (17), was used. In perfusion-weighted imaging, all the academic programs and only one commercial program showed good correlations (r > 0.9) for all three parameters. However, most of these algorithms showed delay dependencies on CBF and MTT. Only two algorithms (PM2 and RP2) did not show any delay dependencies for CBF, CBV, and MTT. For these two algorithms, a circular type of SVD, as described above, is used. For the other programs, use of the same types of circular SVD (P, PG2, and ST2) was also stated; however, our phantom analysis revealed that despite this statement, these programs actually had delay-sensitive errors. When we compared CT perfusion and perfusion-weighted imaging, correlations were generally better in perfusion-weighted imaging than in CT perfusion. The differences of phantom configuration were signal-to-noise ratio, temporal resolution, and scan duration. These factors are intrinsic for perfusion methods; for example, low signal-to-noise ratio, longer temporal resolution, and short scan duration for CT perfusion were generally a result from the aim of reduction for radiation dose. Although CT perfusion has linearity between tracer concentration and signal, accuracy is affected by these factors, compared with perfusion-weighted imaging.
According to a previous CT perfusion study with the use of G1, H, P1, S1, and T1 algorithms, overestimation of the infarcted area because of delay-sensitive CBF reduction was found for G1, P1, and T1 (12). In fact, these three algorithms showed delay sensitivity in our digital phantom analysis. Similarly, it has been reported that G1, H, P1, and T1 show a delay-sensitive MTT increase, and our results with phantoms suggest that these algorithms actually have delay-sensitive errors. Most CT unit manufacturers have recently released new versions of their analysis algorithms (G2, P2, S2, and T2). Delay sensitivity was expected to be improved in these programs; however, three actually displayed delay-induced errors in our phantom analysis. Delay sensitivity has been mainly focused on CBF and MTT (11,17); however, we have shown delay dependency for CBV, as well. Because CBV can be calculated by using the ratio of area under the curve between tissue and large vessel (16), delay-induced truncation of the tissue curve can affect the area under the curve and then CBV.
In addition to these delay sensitivities, other sources of errors, such as true CBV or true MTT dependencies, were evaluated by using our digital phantom. CBF and MTT calculations should ideally be independent of CBV values, and conversely, the CBV calculation should not be affected by MTT values. However, these dependencies were observed in all the algorithms used herein for at least one of the three parameters both for CT perfusion and perfusion-weighted imaging. To increase the accuracy of perfusion analysis, these dependencies should be improved. Further, the shape of R(t) might have a significant effect on quantification of hemodynamic parameters, as R(t) dependencies were found in almost all the algorithms.
In regard to absolute values, slope and intercept in linear regression analysis were found to be significantly variable, suggesting that absolute values cannot be directly compared among different software programs. In addition, we cannot reliably determine the penumbra through threshold levels, nor can we compare any quantitative information between studies conducted by using absolute values. Variations in the absolute values may be partly caused by the difference in basic algorithms, such as SVD and maximum slope, as well as other minor implementations in perfusion analysis. Further, a difference in the intercept causes errors not only in absolute but also in relative values, especially for perfusion-weighted imaging.
Standardization of perfusion analysis is important for multicenter trials. If different programs produce different perfusion results, perfusion images cannot be used for patient selection or estimation of penumbra and final infarction. On the other hand, if standardization is achieved, the results obtained in one study with the use of one software package can be applied to another study with the use of a different program. In the present study, Tmax values of most programs were in good agreement with the values from the Echoplanar Imaging Thrombolysis Evaluation Trial (19), and this fact may facilitate the use of Tmax in large clinical trials in the future, where a number of perfusion analysis programs could be used. Tmax is not a physiologic parameter such as CBF, CBV, and MTT, but researchers (21) have shown that it closely relates to delay, dispersion, and MTT. Validation of perfusion programs by using digital phantom data may also facilitate the development of a more accurate and robust analysis and finally make standardized quality control a reality.
The present study had a number of limitations. First, three types of R(t) were used: exponential, linear, and box shaped. Another shape of R(t) may be used for this simulation (22); however, the true shape of R(t) in the human brain is unknown, and these three types of R(t) are traditionally used in tracer kinetic simulation studies (16,17). Second, the curves were generated only for the first-pass bolus of contrast material, and the second pass was not introduced. In real perfusion data, small peaks are observed at second pass. If the second pass had been included in the simulation, the data may have been more realistic. However, interpretation of results may be more complicated, because the results would be affected by the difference in postprocessing during handling or compensating for second-pass peaks. Third, only the average values for each tile were evaluated. If the standard deviation within a tile had been measured, the difference in the denoising process of each program could have been evaluated. However, our aim was to evaluate not the denoising process but the accuracy and reliability of perfusion analysis. Further studies may be conducted to examine more factors of various parameters, such as noise level, temporal resolution, and R(t), on the basis of our digital phantom scheme. Fourth, we defined accuracy of each algorithm by the correlation coefficient to true values. It has been reported that linearity was lost in the high-flow region in certain types of algorithms, especially for low signal-to-noise ratio (17). However, we used linear regression analysis, as it seemed to be suitable to measure the difference between true and measured values. Fifth, correction for multiple comparisons was not conducted in the analysis of error sources. If the correction is used, statistical comparison may become stricter. However, as the aim of this study was a comparison among different algorithms, a simple and uncorrected comparison was performed.
In conclusion, a digital phantom is a useful tool for evaluating the accuracy and characteristics of CT perfusion and perfusion-weighted imaging perfusion analysis software. Our phantom analysis revealed that all the commercial programs for CT perfusion and perfusion-weighted imaging studied here showed delay-induced errors and/or insufficient correlations with true values, while all the academic programs for perfusion-weighted imaging studied here showed better correlations with true values.
Advances in Knowledge.
• Accuracy and reliability of perfusion analysis software, including tracer-delay sensitivity, can be objectively evaluated by using a digital phantom data set that is based on the widely accepted tracer kinetic theory.
• Correlation with true values embedded in digital phantom data and delay sensitivity were different among software packages and algorithms; however, the academic software had better correlations (r > 0.9) with true values, especially for MR.
• Time to maximum of residue function (Tmax) values in MR were similar in most software packages, and correlations with each other were high (r > 0.9) although none of the commercial software studied here could be used to produce a Tmax map.
Implication for Patient Care.
• Physicians should be careful about the accuracy of analysis software they use, because most of the algorithms in commercial software have delay-induced errors and have additional sources of error that are yet to be elucidated.
Disclosures of Conflicts of Interest: K.K. Financial activities related to the present article: none to disclose. Financial activities not related to the present article: was paid consultancy fee by Medical Image Lab and received payment for lectures including service on speakers bureaus by GE Healthcare and Hitachi Medical Corporation. Other relationships: none to disclose. S.C. No relevant conflicts of interest to disclose. M.S. Financial activities related to the present article: none to disclose. Financial activities not related to the present article: author was paid consultancy fee by Lundbeck; institution was paid consultancy fee by Hitachi Medical; was paid for lectures including service on speakers bureaus by GE Healthcare, Otsuka Pharma, Mitsubishi Pharma, Daiichi Pharma, J-Mac System, Hitachi Medical, Olea Medical, Bayer, Sanofi, and Esai. Other relationships: none to disclose. L.Ø. No relevant conflicts of interest to disclose. H.S. Financial activities related to the present article: none to disclose. Financial activities not related to the present article: paid for board membership by the Japanese Organization of Radiotherapy Quality Management and for consultancy by Medical Image Lab; institution received grants from Hitachi, Hitachi Medical, Varian Medical Systems, Shimadzu, Hokkaido Electric Power, and Elekta K.K.; institution received collaborative research grants from Accuthera, Tanaka Kikinzoku Kogyo K.K., Medikit, Mitsubishi Heavy Industries, Philips Electronics Japan, Fujifilm Medical, Sumitomo Heavy Industries, Shimadzu, Asahikawa Medical University, Nakashima Medical, Hokkaido Gastrointestinal Cancer Study group; institution received consigned research grants from Fujifilm Medical; received payment for lectures including service on speakers bureaus from Moroo, Hitachi, Chiyoda Technol, Japan Society of Medical Physics, Olympus, Varian Medical Systems, and ORIX Life Insurance. Other relationships: none to disclose. K.O. No relevant conflicts of interest to disclose. M.W. Financial activities related to the present article: none to disclose. Financial activities not related to the present article: institution received a grant from GE Healthcare. Other relationships: none to disclose. S.W. No relevant conflicts of interest to disclose.
Supplementary Material
Acknowledgments
The authors thank K. Segawa and H. Kabasawa from GE Healthcare, O. Miyazaki and T. Takahashi from Hitachi Medical Corporation, S. Kuwahara and Y. Suzuki from Philips Electronics Japan, T. Itoh and M. Nielsen from Siemens Healthcare, and Y. Ikeda from Toshiba Medical Systems for their help in the perfusion data analysis.
Received December 8, 2011; revision requested February 3, 2012; final revision received July 5; accepted July 26; final version accepted September 7.
Supported in part by a Grant-in-Aid for Strategic Medical Science Research from the Ministry of Education, Culture, Sports, Science and Technology of Japan and by the Japan Society for the Promotion of Science through the Funding Program for Next Generation World-Leading Researchers (NEXT Program) initiated by the Council for Science and Technology Policy.
Funding: S.W. is an employee of the National Institute of Neurological Disorders and Stroke, National Institutes of Health.
Abbreviations:
- ANOVA
- analysis of variance
- CBF
- cerebral blood flow
- CBV
- cerebral blood volume
- MTT
- mean transit time
- PMA
- Perfusion Mismatch Analyzer
- R(t)
- residue function
- SVD
- singular value decomposition
- Tmax
- time to maximum of R(t)
References
- 1.Klotz E, König M. Perfusion measurements of the brain: using dynamic CT for the quantitative assessment of cerebral ischemia in acute stroke. Eur J Radiol 1999;30(3):170–184 [DOI] [PubMed] [Google Scholar]
- 2.Mayer TE, Hamann GF, Baranczyk J, et al. Dynamic CT perfusion imaging of acute stroke. AJNR Am J Neuroradiol 2000;21(8):1441–1449 [PMC free article] [PubMed] [Google Scholar]
- 3.Lev MH, Segal AZ, Farkas J, et al. Utility of perfusion-weighted CT imaging in acute middle cerebral artery stroke treated with intra-arterial thrombolysis: prediction of final infarct volume and clinical outcome. Stroke 2001;32(9):2021–2028 [DOI] [PubMed] [Google Scholar]
- 4.Jain R, Hoeffner EG, Deveikis JP, Harrigan MR, Thompson BG, Mukherji SK. Carotid perfusion CT with balloon occlusion and acetazolamide challenge test: feasibility. Radiology 2004;231(3):906–913 [DOI] [PubMed] [Google Scholar]
- 5.Laslo AM, Eastwood JD, Chen FX, Lee TY. Dynamic CT perfusion imaging in subarachnoid hemorrhage-related vasospasm. AJNR Am J Neuroradiol 2006;27(3):624–631 [PMC free article] [PubMed] [Google Scholar]
- 6.Cenic A, Nabavi DG, Craen RA, Gelb AW, Lee TY. A CT method to measure hemodynamics in brain tumors: validation and application of cerebral blood flow maps. AJNR Am J Neuroradiol 2000;21(3):462–470 [PMC free article] [PubMed] [Google Scholar]
- 7.Olivot JM, Mlynash M, Thijs VN, et al. Optimal Tmax threshold for predicting penumbral tissue in acute stroke. Stroke 2009;40(2):469–475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Davis SM, Donnan GA. Advances in penumbra imaging with MR. Cerebrovasc Dis 2004;17(Suppl 3):23–27 [DOI] [PubMed] [Google Scholar]
- 9.Rose SE, Janke AL, Griffin M, Finnigan S, Chalk JB. Improved prediction of final infarct volume using bolus delay-corrected perfusion-weighted MRI: implications for the ischemic penumbra. Stroke 2004;35(11):2466–2471 [DOI] [PubMed] [Google Scholar]
- 10.Sasaki M, Kudo K, Honjo K, Hu JQ, Wang HB, Shintaku K. Prediction of infarct volume and neurologic outcome by using automated multiparametric perfusion-weighted magnetic resonance imaging in a primate model of permanent middle cerebral artery occlusion. J Cereb Blood Flow Metab 2011;31(2):448–456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kudo K, Sasaki M, Ogasawara K, Terae S, Ehara S, Shirato H. Difference in tracer delay-induced effect among deconvolution algorithms in CT perfusion analysis: quantitative evaluation with digital phantoms. Radiology 2009;251(1):241–249 [DOI] [PubMed] [Google Scholar]
- 12.Kudo K, Sasaki M, Yamada K, et al. Differences in CT perfusion maps generated by different commercial software: quantitative analysis by using identical source data of acute stroke patients. Radiology 2010;254(1):200–209 [DOI] [PubMed] [Google Scholar]
- 13.Christensen S, Mouridsen K, Wu O, et al. Comparison of 10 perfusion MRI parameters in 97 sub-6-hour stroke patients using voxel-based receiver operating characteristics analysis. Stroke 2009;40(6):2055–2061 [DOI] [PubMed] [Google Scholar]
- 14.Dani KA, Thomas RG, Chappell FM, et al. Computed tomography and magnetic resonance perfusion imaging in ischemic stroke: definitions and thresholds. Ann Neurol 2011;70(3):384–401 [DOI] [PubMed] [Google Scholar]
- 15.Wintermark M, Albers GW, Alexandrov AV, et al. Acute stroke imaging research roadmap. Stroke 2008;39(5):1621–1628 [DOI] [PubMed] [Google Scholar]
- 16.Ostergaard L, Weisskoff RM, Chesler DA, Gyldensted C, Rosen BR. High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. I. Mathematical approach and statistical analysis. Magn Reson Med 1996;36(5):715–725 [DOI] [PubMed] [Google Scholar]
- 17.Wu O, Østergaard L, Weisskoff RM, Benner T, Rosen BR, Sorensen AG. Tracer arrival timing-insensitive technique for estimating flow in MR perfusion-weighted imaging using singular value decomposition with a block-circulant deconvolution matrix. Magn Reson Med 2003;50(1):164–174 [DOI] [PubMed] [Google Scholar]
- 18.Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol 1954;6(12):731–744 [DOI] [PubMed] [Google Scholar]
- 19.Davis SM, Donnan GA, Parsons MW, et al. Effects of alteplase beyond 3 h after stroke in the Echoplanar Imaging Thrombolytic Evaluation Trial (EPITHET): a placebo-controlled randomised trial. Lancet Neurol 2008;7(4):299–309 [DOI] [PubMed] [Google Scholar]
- 20.Straka M, Albers GW, Bammer R. Real-time diffusion-perfusion mismatch analysis in acute stroke. J Magn Reson Imaging 2010;32(5):1024–1037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Calamante F, Christensen S, Desmond PM, Ostergaard L, Davis SM, Connelly A. The physiological significance of the time-to-maximum (Tmax) parameter in perfusion MRI. Stroke 2010;41(6):1169–1174 [DOI] [PubMed] [Google Scholar]
- 22.Mouridsen K, Friston K, Hjort N, Gyldensted L, Østergaard L, Kiebel S. Bayesian estimation of cerebral perfusion using a physiological model of microvasculature. Neuroimage 2006;33(2):570–579 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.