Fast hydrogen exchange affects ¹⁵N relaxation measurements in intrinsically disordered proteins

Abstract

Unprotected amide protons can undergo fast hydrogen exchange (HX) with protons from the solvent. Generally, NMR experiments using the out-and-back coherence transfer with amide proton detection are affected by fast HX and result in reduced signal intensity. When one of these experiments, ¹H-¹⁵N HSQC, is used to measure the ¹⁵N transverse relaxation rate (R₂), the measured R₂ rate is convoluted with the HX rate (k_HX) and has higher apparent R₂ values. Since the ¹⁵N R₂ measurement is important for analyzing protein backbone dynamics, the HX effect on the R₂ measurement is investigated and described here by multi-exponential signal decay. We demonstrate these effects by performing ¹⁵N R₂^CPMG experiments on α-synuclein, an intrinsically disordered protein (IDP), in which the amide protons are exposed to solvent. We show that the HX effect on R₂^CPMG can be extracted by the derived equation. In conclusion, the HX effect may be pulse sequence specific and results from various sources including the J coupling evolution, the change of steady state water proton magnetization, and the D₂O content in the sample. To avoid the HX effect on the analysis of relaxation data of unprotected amides, it is suggested that NMR experimental conditions insensitive to the HX should be considered or that intrinsic R₂^CPMG values be obtained by methods described herein.

Introduction

¹⁵N backbone transverse relaxation experiments (R₂) using the CPMG (Carr–Purcell–Meiboom–Gill) pulse train (¹⁵N R₂^CPMG) have been used to investigate dynamics of backbone amides in globular proteins (Farrow et al. 1994; Kay et al. 1989; Mandel et al. 1995) and have also been applied to study NMR dynamics of intrinsically disordered proteins (IDPs) (Buevich and Baum 1999; Buevich et al. 2001; Eliezer 2009; Mittag and Forman-Kay 2007; Wright and Dyson 2009). ¹⁵N R₂^CPMG rates have been important indicators for protein backbone dynamics and have provided information about the structural mobility on the ps to ns timescale and about conformational exchange processes on the μs to ms timescale (Mittermaier and Kay 2009; Palmer III 2004; Wang and Palmer 2003). When backbone amide protons in proteins are not protected from the solvent water, those protons undergo fast hydrogen exchange (HX). Although HX rates of amide protons and R₂^CPMG rates of amide nitrogens are measurements of different events in protein dynamics, fast HX may affect the measurement of ¹⁵N R₂^CPMG rates. Since ¹⁵N R₂^CPMG rates are measured indirectly with ¹H-¹⁵N HSQC using the out-and-back coherence transfer with a prolonged relaxation time in the pulse sequence, measured rates can be modulated due to the signal intensity of the HSQC vulnerable to fast HX. Some NMR experiments have been designed to measure fast HX rates indirectly during the ¹⁵N time evolution or relaxation. In the R_1zz relaxation experiment of two spin order (N_zH_z) (Skrynnikov and Ernst 1999), the HX effect destroys the N_zH_z spin operator and this results in the combined HX and R_1zz relaxation rate. In the ¹⁵N R₂ relaxation experiment of the HCN-type coherence transfer (Kateb et al. 2007), the fast HX effect that dephases the ¹⁵N spin operator is correlated with the ¹J_NH coupling evolution. The presence or absence of ¹H decoupling during the relaxation time results in a significant difference in the HX effect on ¹⁵N R₂ relaxation rates. In the ¹⁵N^H/D-SOLEXSY experiment using the (HACACO)NH pulse sequence, H/D exchange rates were measured during the ¹⁵N t₁ evolution in H₂O/D₂O (50%/50%) (Chevelkov et al. 2010). Based on these experiments, it is expected that the ¹⁵N R₂^CPMG relaxation rate measured by the HSQC-type NMR experiments may be modulated by fast HX although the mechanism of the HX effect is different from previously reported mechanisms and includes the spin state of ¹⁵N, the J-coupling evolution, or the solvent environment.

Here we show that R₂^CPMG rates are modulated by fast HX rates in α-synuclein (αSyn), a protein associated with Parkinson’s disease (Chiti and Dobson 2006; Goedert 2001). If ¹⁵N R₂^CPMG rates are modulated by both conformational exchange and HX, it will be complicated to interpret the relaxation data without knowing the magnitude of the HX effect on the ¹⁵N R₂^CPMG rates. In particular, when residues with large conformational exchange are located at the solvent accessible surface areas, ¹⁵N R₂^CPMG rates may be a combination of both conformational exchange and fast HX rates (Bertini et al. 2002; Tugarinov and Kay 2003). αSyn is an intrinsically disordered protein (IDP) (Eliezer et al. 2001; Uversky et al. 2000; Wu et al. 2008) and forms structurally disordered ensembles in solution which possess enhanced HX rates at neutral pH and high temperature (Croke et al. 2008). We demonstrate the relationship between fast HX and the ¹⁵N R₂^CPMG rates at different pH states and show that the ¹⁵N relaxation rates that are affected by fast HX can be corrected quantitatively. The methods discussed here may be applied to other IDPs or partially folded proteins that are studied at neutral pH to distinguish the inherent R₂ values from those associated with fast hydrogen exchange.

Materials and methods

Preparation of αSyn protein

The expression and purification of ¹⁵N-labeled αSyn was done by previously described protocols (Wu et al. 2009). Lyophilized αSyn was dissolved in phosphate buffer at pH 7.4 and 6.2 (10 mM phosphate, 137 mM NaCl, 2 mM KCl). Prior to applying NMR experiments, samples were filtered by a 100 kDa filter (Millipore) to remove invisible small aggregates. Final sample concentrations were adjusted to 250 μM with 10% (v/v) D₂O for all NMR experiments.

NMR data acquisition

The ¹⁵N R₂^CPMG experiment was performed using a modified pulse sequence of gNhsqc from the Varian BioPack library; the main modification is an optional condition for the proton steady state (SS) pulse in the beginning of the pulse sequence (Fig. 2). The NMR data were collected twice at a proton frequency of 800 MHz and 15 °C without and with the SS pulse. Relaxation time delays for R₂^CPMG experiments were 0.01, 0.03, 0.05, 0.07, 0.09, 0.13, 0.17, 0.21, and 0.25 (s) at pH 7.4 and pH 6.2. The CPMG inter-pulse delay (2τ) was 1.25 ms and the recycle delay (d₁) for each scan was 2 seconds. Spectral complex points were 1024 and 256 in the t₂ and t₁ dimensions, respectively. Relaxation data were acquired by interleaving relaxation time delays and t₁ increments. Data were processed and analyzed by NMRPipe (Delaglio et al. 1995). The relaxation data were fit by two different methods to measure the apparent R₂^CPMG values; (1) single exponential fit as described in other previous studies (Bertoncini et al. 2007; Bussell and Eliezer 2001) and (2) multi-exponential fit introduced in this paper (discussed in results) to remove the HX effect.

Fig. 2.

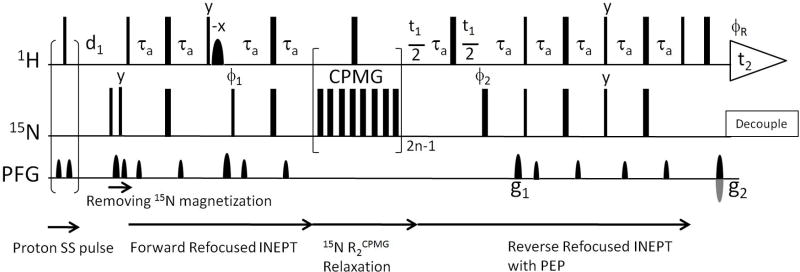
The ¹⁵N R₂^CPMG pulse sequence. The gNhsqc (with T2 = ‘y’) from the Varian BioPack library is outlined. 90° and 180° hard pulses are represented by narrow and wide rectangles. Pulse phases are written on the pulses but if not mentioned, phases are on the x-axis. The sinc shaped water flip-back pulse is used during the forward refocused INEPT to minimize the water saturation by bringing the water magnetization to the z-axis. Delay τ_a is 0.25/¹J_NH. Phase cycles are φ₁ = x, −x, φ₂ = x, x, y, y, −x, −x, −y, −y, and φ_R = x, −x, −x, x. To test the HX effect, an optional proton steady state (SS) pulse is introduced in the beginning of the pulse sequence. The implemented SS pulse is gradient – RF pulse – gradient where the RF pulse is a proton 90° hard pulse and the gradient is the strength of 10 gauss/cm and the duration of 0.5. 2n-1 ( = 1, 3, 5, etc) cycles of ¹⁵N CPMG pulse trains are applied for the R₂^CPMG measurement where the single cycle takes the 10 ms relaxation delay and a 180° proton pulse. The inter-pulse delay between 180° ¹⁵N pulses in CPMG is 1.25 ms. The gNhsqc adapts the sensitivity enhanced HSQC with PEP (Preservation and Equivalent Pathways) and the gradient coherence selection (by g₁ and g₂). Other experimental details are available from Varian BioPack.

To measure hydrogen exchange rates (k_HX), CLEANEX (Hwang et al. 1998) experiments including a fast ¹H-¹⁵N HSQC detection scheme were performed by using the pulse sequence of gCLNfhsqc from the Varian BioPack library. The following mixing times were used; 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07 (s) at pH 7.4 and 0.01, 0.02, 0.04, 0.06, 0.08, 0.1, 0.12 (s) at pH 6.2. The reference fast ¹H-¹⁵N HSQC spectra were acquired to serve as V₀ in the recommended fitting equation (Hwang et al. 1998). The recycle delay for each scan was 2 seconds and spectral complex points were 1024 and 256 in the t₂ and t₁ dimensions, respectively. Hydrogen exchange data were acquired by interleaving mixing times and t₁ increments. Data were processed and analyzed by NMRPipe (Delaglio et al. 1995). The intensity build-ups by mixing times were fitted to obtain two unknown k_HX and R_{1A, app} (apparent R₁ of amide protons) with a fixed R_{1B, app} (apparent R₁ of water protons, 0.6 Hz).

Results and Discussion

The ¹⁵N R₂^CPMG relaxation data of αSyn acquired at pH 7.4 and pH 6.2 (Fig. 1) were acquired by using the pulse sequence (Fig. 2) without the proton steady state pulse and the data were analyzed with single exponential fits as described in other previous studies (Bertoncini et al. 2007; Bussell and Eliezer 2001). The resulting ¹⁵N R₂^CPMG values showed that values at pH 7.4 were elevated relative to those at pH 6.2 and also showed some sequence-specific differences; specifically the N-terminal residues have slightly larger values overall than the C-terminal residues (Fig. 1). Individual R₂^CPMG values showed non-uniform deviations along residues and averages of reported ¹⁵N R₂^CPMG values were 4.21 ± 0.55 Hz at pH 7.4 and 3.54 ± 0.46 Hz at pH 6.2. The discrepancy in ¹⁵N R₂^CPMG values between two pH’s may arise from changes in dynamics of αSyn or by changes in conformational exchange or folding states of the protein.

Fig. 1.

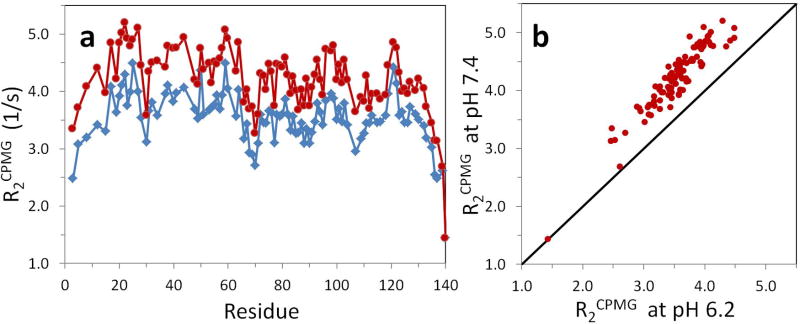
(a) Apparent R₂^CPMG values of αSyn at pH 7.4 (red circles) and pH 6.2 (blue rhombi) at 15°C. R₂^CPMG relaxation data acquired without the proton SS pulse (Fig. 2) were fit with a single exponential decay function. There are large and systematic differences between them in addition to small random deviations. (b) Correlation between R₂^CPMG values at pH 7.4 and pH 6.2.

However, pH-dependent water hydrogen exchange (HX) rates of amide protons may be a primary cause for large differences in ¹⁵N R₂^CPMG values since αSyn is known as an IDP (Eliezer et al. 2001; Uversky et al. 2000; Weinreb et al. 1996; Wu et al. 2008) and measurement of HX rates show that the protein undergoes very fast HX on the order of 5 to 20 Hz (Croke et al. 2008) and that its amide protons are not protected from H/D hydrogen exchange. In Supporting Information, HSQC spectra of αSyn acquired at various experimental conditions were similar to each other except for the residue H50 due to the pH titration of the imidazole. This supports that the intrinsic properties (including R₂^CPMG values) of αSyn are similar to each other at pH7.4 and pH 6.2. In this paper, we show that the pH-dependent differences in ¹⁵N R₂^CPMG can be derived from the pH-dependent hydrogen exchange (HX) rates. Improvement of the correlation between ¹⁵N R₂^CPMG values between pH 7.4 and pH 6.2 is demonstrated and ¹⁵N R₂^CPMG values without HX effect are obtained.

To describe the HX effect on the backbone ¹⁵N R₂^CPMG NMR experiment, the conventional H/D exchange (exchange between amide hydrogen and solvent deuterium) is considered as one of HX mechanisms because of the mixed solvent environment of 90% H₂O and 10% D₂O. For H/D exchange, it is assumed temporarily that the protein ¹⁵N spin is 100% locked in the N_x spin state during the ¹⁵N relaxation measurement period (t) and H/H exchange (exchange between amide hydrogen and solvent hydrogen) has no HX effect. The pulse sequence of the ¹⁵N R₂^CPMG NMR experiment using refocused HSQC is outlined in Fig. 2. The out-and-back nature of HSQC requires the NH chemical integrity, which selects the protein-NH by forward refocused INEPT and detects the same protein-NH by reverse refocused INEPT. By H/D exchange, the in-phase N_x spin state (H_EN_x) after forward refocused INEPT can lose the attached H population (H_E) and the deuterium populated D_EN_x spin state is generated. Then, the D_EN_x state fails to produce the NMR signal through reverse refocused INEPT.

In H/D exchange, the loss of proton occupancy on the amide is directly proportional to the D₂O content in the solvent. When H₂O/D₂O fractions in the mixed solvent are Q/(1-Q), populations of NH/ND are Q/(1-Q) in equilibrium. However, the initial NH population selected by the forward refocused INEPT is repopulated into NH and ND by multiplying Q and (1-Q) if HX is completed during the relaxation period. Since the reverse refocused INEPT selects only the NH population, the HSQC signal is subject to signal loss by a maximum of (1-Q). By introducing the HX rate constant (k_HX), the NMR signal intensity decay (I) can be a multi-exponential in equation 1 in combination with the ¹⁵N R₂^CPMG during the CPMG relaxation time (t).

$$I(t)=I_0\{Q+(1-Q)e^{-k_{HX}t}\}{e}^{-R_2^{\mathit{CPMG}}t}$$ (1)

Equation 1 is valid when the pseudo-first order kinetics can be applied for HX at the slow exchange regime (k_HX < R₂^CPMG). At prolonged relaxation times under k_HX > R₂^CPMG, HX reaches equilibrium and the backward exchange (from ND to NH) cannot be ignored in the time scale of the R₂^CPMG relaxation. This requires the Bloch-McConnell equation for chemical exchange (Hansen and Led 2003; McConnell 1958) which includes two different R₂^CPMG rates (R₂^NH for the protonated nitrogen and R₂^ND for the deuterated nitrogen) instead of a single R₂^CPMG in equation 1. At the extreme fast exchange (k_HX ≫ R₂^NH), the R₂^CPMG (from equation 1) appears as a population-weighted average of R₂^NH and R₂^ND and the relative error of R₂^CPMG (from equation 1) to R₂^NH (from Bloch-McConnell equation) is a maximum of 5.5 % in our calculation (see Supporting Information). Especially under our experimental conditions (k_HX / R₂^CPMG ≤ about 10 and Q = 0.9), the relative error of R₂^CPMG is estimated to be less than 4.5 % (see Supporting Information). Since it is difficult to obtain R₂^NH and R₂^ND separately from a single data set of a multi-exponential signal decay, equation 1 can be used as a good approximation to interpret the HX effect resulting in the large difference of R₂^CPMG values as shown in Figure 1.

In the case of H/H exchange happening during the ¹⁵N relaxation time period (t), the H_EN_x state needs to be elaborated by using single element spin operators; H_EN_x = (0.5H^α + 0.5H^β)N_x to understand the role of the exchanged protons. By H/H exchange, an exchanging proton spin replaces H^α and H^β with c₁H^α + c₂H^β where c₁ and c₂ are probability coefficients from the water proton and their ensemble averages are 0.5 each. As shown in equation 2, coefficients (c₁ and c₂) of the exchanged H are not correlated with coefficients of 0.5 but the ensemble average generates the original H_EN_x spin state back. If the water proton magnetization has c₁ = 0.5 + δ and c₂ = 0.5 − δ where δ indicates a negligible population difference, the exchanged H_zN_x term does not contribute to the signal through the reverse refocused INEPT. Thus the result of H/H exchange during the ¹⁵N R₂^CPMG relaxation has no effect on the N_x spin operator.

$$\begin{array}{l}{H}_E{N}_x=(0.5H^{\alpha }+0.5H^{\beta })N_x\\ \stackrel{HX}{\to }\{0.5(c_1{H}^{\alpha }+c_2{H}^{\beta })+0.5(c_1{H}^{\alpha }+c_2{H}^{\beta })\}{N}_x\\ =\{(0.5H^{\alpha }+0.5H^{\beta })+\delta (0.5H^{\alpha }-0.5H^{\beta })\}{N}_x\\ =(H_E+H_z)N_x\\ \approx H_E{N}_x\end{array}$$ (2)

The H/H exchange needs an additional consideration which is not necessary for H/D exchange since protons are the directly observed nucleus and variable pulses and durations are applied. In the pulse sequence (Fig. 2), 180° pulses are incremented by 2n-1 with the increase of the ¹⁵N R₂^CPMG relaxation delay (t). Even though the experiment starts with many dummy scans to reach a steady state, we need to be careful about the relationship between the maintenance of the steady state and the increase in the R₂^CPMG relaxation delay. The different number of proton pulses and delays with an increase in the ¹⁵N R₂^CPMG relaxation delay may perturb the steady state of the proton magnetization, particularly the bulk water proton magnetization. The pulse sequence (Fig. 2) is designed to minimize the saturation of the water proton magnetization but additional pulses and delays may result in increased saturation of the water proton magnetization. With the increment in the number of 180° proton pulses, the water proton magnetization may be partially and progressively saturated. This causes a different amount of HX between amide and water protons during the fixed recycle delay (d₁) when d₁ is shorter than at least 5 times the water T₁ relaxation time which is a typical experimental condition. It means that the steady state of the water proton magnetization can be altered depending on the ¹⁵N R₂^CPMG relaxation delay and it modulates the steady state of the amide proton magnetization through HX.

It will be difficult to quantify how much water proton magnetization is affected by proton pulses and delays during the ¹⁵N R₂^CPMG relaxation delay due to radiation damping but this effect can be removed by applying a steady state (SS) pulse (or a purge pulse) right after the acquisition time (t₂) and before the recycle delay (d₁). The proton SS pulse destroys the effect of the water flip-back pulse designed for minimizing water saturation (Fig. 2) and randomizes (saturates and dephases) the water proton magnetization right after acquisition. Although the SS pulse attenuates the ¹H-¹⁵N HSQC signal intensity through HX when the amide hydrogen is under fast HX, it will ensure that the same amount of H/H exchange happens during the d₁ delay regardless of the change of pulses and delays in the pulse sequence. For this reason, ¹⁵N R₂^CPMG experiments were run with and without the proton SS pulse to test HX effect. The implemented SS pulse in the ¹⁵N R₂^CPMG experiment is gradient - ¹H 90° pulse - gradient in Fig. 2 but the other type of SS pulses such as the x-axis trim pulse followed by the y-axis trim pulse will be effective, as well.

When the in-phase N_x spin state is not locked completely by the CPMG pulses during the relaxation period, a minor population of anti-phase ¹⁵N magnetization is present by the ¹J_NH coupling evolution. The HX effect on the anti-phase ¹⁵N magnetization (2N_yH_z) will be different from the HX effect on the in-phase magnetization N_x. The H/H exchange effect on 2N_yH_z (equation 3) is considered in a similar way to the case of the H/H exchange of the in-phase N_x spin state (equation 2). The resulting coefficients of (c₁ – c₁) and (c₂ – c₂) by HX will become zero by ensemble averaging.

$$\begin{array}{l}2H_z{N}_y=(0.5H^{\alpha }-0.5H^{\beta })N_y\\ \stackrel{HX}{\to }\{0.5(c_1{H}^{\alpha }+c_2{H}^{\beta })-0.5(c_1{H}^{\alpha }+c_2{H}^{\beta })\}{N}_y\\ =\{0.5(c_1-c_1)H^{\alpha }+0.5(c_2-c_2)H^{\beta }\}{N}_y\\ \approx \mathit{zero}\end{array}$$ (3)

Since in-phase and anti-phase spin states undergo different HX effect, in-phase / anti-phase populations in the ¹⁵N R₂^CPMG NMR experiment need to be known and have been formulated in equation 4 through the time-averaged R₂ of the exchanging in-phase and anti-phase magnetizations via J-coupling

$$R_2^{\mathit{CPMG}}=0.5\{1+sinc(2\pi J\tau )\}{R}_2^{in}+0.5\{1-sinc(2\pi J\tau )\}{R}_2^{\mathit{anti}}$$ (4)

where R₂ⁱⁿ and R₂^anti are transverse relaxation rates of in-phase and anti-phase spin states, J is the ¹J_NH coupling constant, and is the CPMG refocusing delay (Griesinger and Ernst 1988; Palmer III et al. 1992). Coefficients of R₂ⁱⁿ and R₂^anti are effective fractions of in-phase and anti-phase states; f_in = 0.5{1+sinc(2πJτ)} and f_anti = 0.5{1-sinc(2πJτ)}. The fraction of the anti-phase state (f_anti) is estimated as 0.011 with τ = 0.625ms and ¹J_NH = 93Hz under the experimental conditions. Since the HX effect on ¹⁵N relaxation is included only in the anti-phase spin state, the apparent R₂ (R₂^app) is approximated by R₂^CPMG + f_antik_HX which includes the HX effect along with equation 4. By combining this and equation 1, the resulting multi-exponential function for HX effect is in equation 5.

$$I(t)=I_0\{{Qe}^{-f_{\mathit{anti}}{k}_{HX}t}+(1-Q)e^{-k_{HX}t}\}{e}^{-R_2^{\mathit{CPMG}}t}$$ (5)

Thus the total HX effect in the ¹⁵N R₂^CPMG NMR experiment using refocused HSQC results from the combined effects of H/D exchange, H/H exchange, and in-phase/anti-phase J-coupling exchange. A relevant kinetic model is presented in scheme 1 and the derivation of equation 5 is in Supporting Information. In scheme 1, the total k_HX was divided into Qk_HX and (1-Q)k_HX where Q is the preserved hydrogen fraction through H/H exchange. Therefore, Qk_HX is the H/H exchange rate and (1-Q)k_HX is the H/D exchange rate in the mixed solvent of H₂O and D₂O. The multi-exponential fit of the R₂^CPMG relaxation data with five parameters (I₀, Q, f_anti, k_HX, and R₂) shown in equation 5 is not plausible but can be reduced to a fit with two unknown parameters (I₀ and R₂) and with three known Q, f_anti, and k_HX parameters. Since Q (= 0.9) and f_anti (= 0.011) are estimated from the H₂O content and the anti-phase fraction under the controlled experimental condition, k_HX rates need to be measured separately.

Scheme 1.

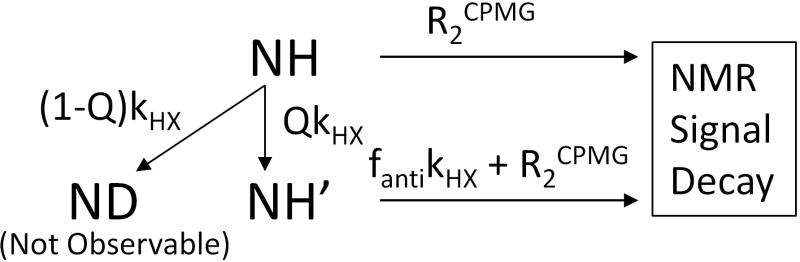
Hydrogen exchange effect during the ¹⁵N R₂ relaxation time period. The H/H exchange rate is Qk_HX and the H/D exchange rate is (1-Q)k_HX when the H₂O content in the sample solvent is Q and the D₂O content is (1-Q). In H/H exchange, the product NH′ is distinguished from the reactant NH.

To find k_HX, the CLEANEX (Hwang et al. 1998) experiments were performed at pH 7.4 and pH 6.2 and measured k_HX rates of αSyn were plotted in Fig. 3. The k_HX values at pH 7.4 are significantly different from the values at pH 6.2 and also show variations across the protein sequence. Compared to the apparent R₂^CPMG values (Fig. 1) obtained from the single exponential decay, the difference in overall k_HX values between pH 7.4 and pH 6.2 were much greater than the difference in apparent R₂^CPMG values indicating that the R₂^CPMG experiment suppresses a significant amount of the HX effect despite the fact that the HX effect is still observable on the apparent R₂^CPMG values.

Fig. 3.

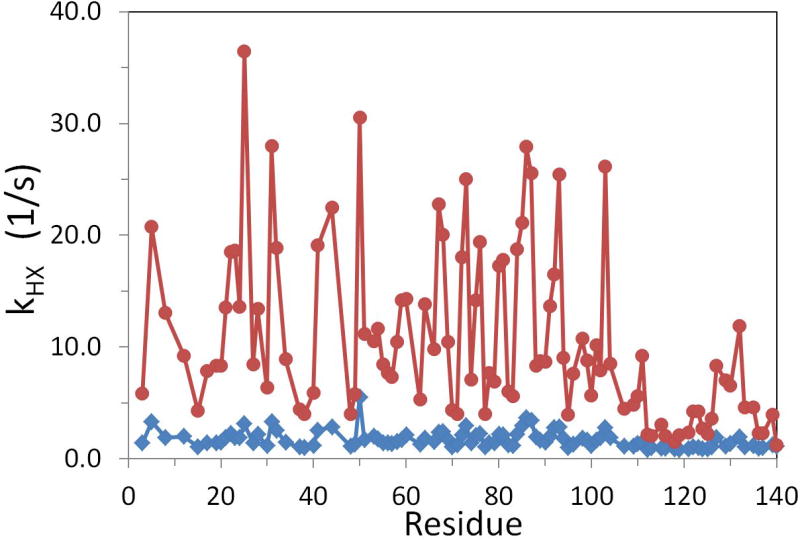
pH-dependent k_HX values. k_HX values of αSyn were measured by CLEANEX method at pH 7.4 (red circles) and pH 6.2 (blue rhombi) at 15 °C. The large increase of k_HX values at pH 7.4 is prominent by increasing pH.

To ensure the steady state of amide and water proton magnetization, the R₂^CPMG pulse sequence with the proton SS pulse (Fig. 2) was used and R₂^CPMG relaxation data were acquired again at pH 7.4 and pH 6.2. With Q = 0.9, f_anti = 0.011, and known k_HX values from Fig. 3, multi-exponential fits to the R₂^CPMG relaxation data were performed with equation 5. The optimized R₂^CPMG values at pH 7.4 and pH 6.2 were plotted in Fig. 4. The large discrepancies in the apparent R₂^CPMG values of αSyn shown in Fig. 1 were eliminated by including the HX effect in the data analysis. R₂^CPMG values at pH 7.4 reported in Fig. 1 were corrected more than pH 6.2, R₂^CPMG values since k_HX values at pH 7.4 were generally much greater than these values at pH 6.2. Average ¹⁵N R₂^CPMG values at pH 7.4 and pH 6.2 in Fig. 4 were 3.27 ± 0.46 Hz and 3.13 ± 0.44 Hz and the difference of average R₂^CPMG values between two pH’s was reduced to 0.14 Hz comparing to the difference of 0.67 in Fig. 1.

Fig. 4.

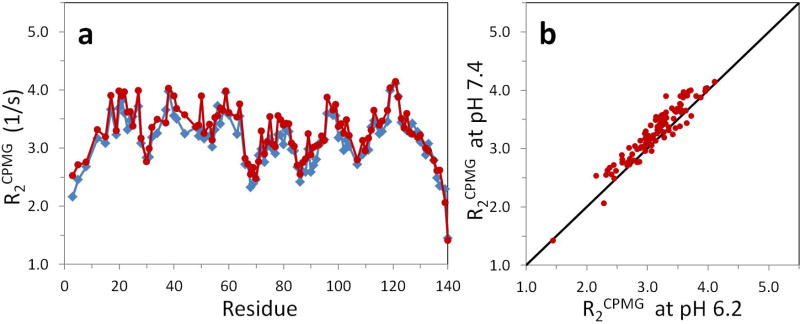
(a) Corrected R₂^CPMG values at pH 7.4 and 6.2. R₂^CPMG values at pH 7.4 (red circles) and pH 6.2 (blue rhombi) were obtained with the multi-exponential decay function (equation 5) using Q = 0.9, f_anti = 0.011, and k_HX values from Fig. 3. The relaxation data were acquired with the SS pulse. The large differences seen in Fig. 1 were corrected. (b) Correlation between R₂^CPMG values at pH 7.4 and pH 6.2.

To demonstrate how the HX impacts on the R₂^CPMG relaxation data, examples of the relaxation data with (filled squares) and without (filled circles) the proton SS pulse were plotted in Fig. 5 for residue G25 under fast HX (k_HX = 36.3 Hz) at pH 7.4. Regardless of the SS pulse, multi-exponential fittings (solid lines) resulting from equation 5 improve the goodness of fit comparing to single exponential fittings (dotted line) in the presence of fast HX. Between multi-exponential fits of relaxation data with and without the proton SS pulse, it may be hard to judge whether the resulted R₂^CPMG values are correct or not by comparing the goodness of fits. However, R₂^CPMG values from the use of the SS pulse are smaller than those resulting from no SS pulse and represent the R₂^CPMG values without HX effect. The overall good agreement of the R₂^CPMG values between pH 7.4 and pH 6.2 (Fig. 4) can be achieved by acquiring the relaxation data with the proton SS pulse and analyzing the data with equation 5. Therefore, in the presence of observable HX, the R₂^CPMG relaxation data are affected by HX and these corrections are favorable.

Fig. 5.

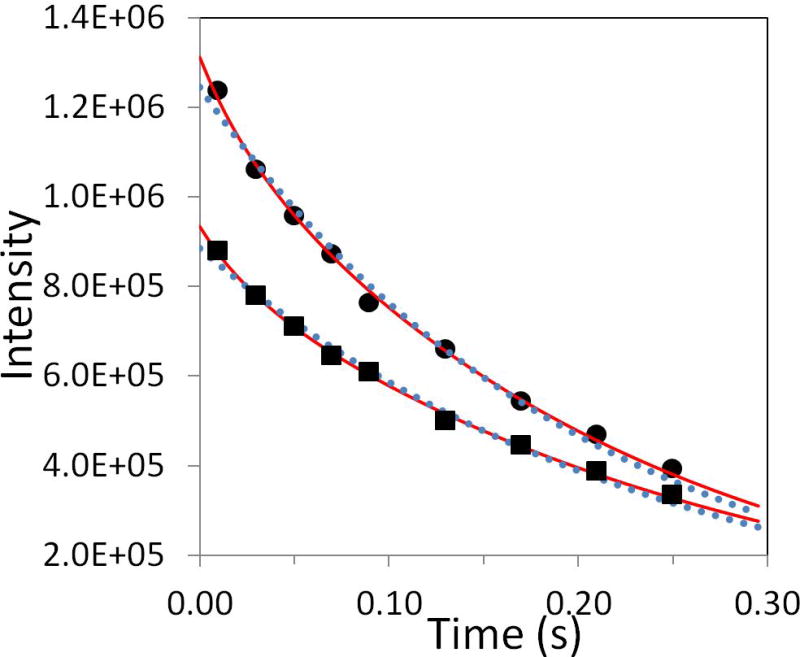
Examples of data fitting for residue G25. Experimental R₂^CPMG relaxation data for residue G25 at pH 7.4 were obtained with and without the proton SS pulse. The data (filled circles) without the proton SS pulse were fit with a single exponential (dotted line, I₀ = 1.25×10⁶, R₂^CPMG = 4.90 Hz, and R² = 99.1 %) and a multi-exponential (equation 5) (solid line, I₀ = 1.31×10⁶, Q = 0.9, f_anti = 0.011, k_HX = 36.3 Hz, R₂^CPMG = 4.13 Hz, and R² = 99.8 %), where R² is the coefficient of determination for the goodness of fit. The data (filled squares) with the proton SS pulse were also fit with a single exponential (dotted line, I₀ = 8.85×10⁵, R₂^CPMG = 4.11 Hz, and R² = 99.2 %) and a multi-exponential (equation 5) (solid line, I₀ = 9.35×10⁵, Q = 0.9, f_anti = 0.011, k_HX = 36.3 Hz, R₂^CPMG = 3.37 Hz, and R² = 99.8 %).

In the presence of fast HX, it seems difficult to eliminate the HX effect in the R₂^CPMG experiment and also hard to identify the HX effect in the data analysis as shown in Fig. 5. Using a protein sample prepared in 100% H₂O (Iwahara et al. 2007) will suppress the HX effect on R₂^CPMG data but incomplete suppression is still expected due to no control of the water proton magnetization by the steady state pulse and the anti-phase populations. Without correcting the HX effect, the elevated apparent R₂^CPMG values could be mis-interpreted as a result of other contributions such as conformational exchange or protein aggregation. In this context, conformational exchange of αSyn proposed at 37 °C may be due to HX effect on R₂^CPMG at these high temperatures (McNulty et al. 2006). When ¹H-¹⁵N HSQC signal intensities are vulnerable by removing the water flip-back pulse and dephasing the water magnetization (Chen and Tjandra 2011), fast HX may play a role to attenuate the the signal intensity because of saturated water magnetization. In that situation, the HX effect needs to be under control in the acquisition scheme and in the data analysis as proposed here.

To minimize the HX effect on the R₂^CPMG experiment, relaxation rates need to be obtained by working under conditions for which fast HX does not exist such as low temperatures and low pH’s. In Supporting Information, dramatic intensity changes of HSQC spectra by HX effect were demonstrated by acquiring spectra at (pH 7.4, 35 °C), (pH 7.4 15 °C), (pH 6.1, 35 °C), and (pH 6.1, 15 °C). When sample conditions for removing fast HX cannot be obtained, we have shown that the ¹⁵N R₂^CPMG pulse sequence needs to contain SS pulses in order to remove water saturation effects and that quantitative corrections of the ¹⁵N relaxation rates for fast HX need to be performed. When the experiment is performed on a protein sample in mixed H₂O/D₂O solvent, use of the multi-exponential fit to the ¹⁵N R₂^CPMG relaxation data by equation 5 is a necessary to extract ¹⁵N R₂^CPMG values without HX effect. Other approaches that may simplify the data analysis include running the experiment in 100%H2O as practiced by Clore’s group (Iwahara et al. 2007). This removes the H/D exchange effect and the multi-exponential fit by equation 5 is changed to the single exponential fit with the rate constant of (f_anti · k_HX + R₂^CPMG). The required HX rates in data analysis can be measured independently from R_1zz (Skrynnikov and Ernst 1999), MEXICO (Gemmecker et al. 1993), CLEANEX (Hwang et al. 1998), or ¹⁵N^H/D-SOLEXSY (Chevelkov et al. 2010) experiments. As an alternative to R₂^CPMG, the ¹⁵N R_1ρ experiment has been also used for R₂ measurement after correction of off-resonance effects (Korzhnev et al. 2002; Palmer III et al. 2001). If the anti-phase population is negligible (f_anti ≅ 0) in the ¹⁵N R_1ρ experiment by applying a strong spin-lock on N_x, then equation 5 becomes the single exponential fit with the rate constant of R_1ρ with the use of 100% H₂O. A noticeable merit of this approach is no requirement of measuring k_HX values. However, it is important that the SS pulses are used for any variation of experiments to assure the steady state HX equilibrium during the inter-scan recycle delay.

Although we demonstrated the HX effect on the backbone ¹⁵N R₂^CPMG relaxation data applied to the IDP αSyn, the HX effect may be present in other protein samples and various NMR experiments. In addition to IDPs, globular proteins with unstructured elements such as large loop regions, or partially folded proteins that have a large number of amides exposed to the solvent may have increased apparent ¹⁵N R₂^CPMG values due to fast HX. Other NMR experiments that have long evolution times to measure relaxation and diffusion should be potentially considered for modulation by fast HX effects as well (Dempsey 2001; Zhang et al. 1995). Like ¹⁵N R₂^CPMG experiments, NMR experiments that use the indirect detection scheme also need to be considered with caution although heteronuclear NMR properties other than ¹H are observed.