Figure 1.

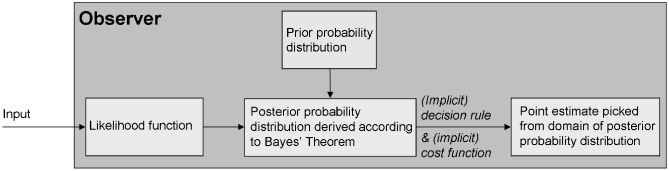
The standard Bayesian observer model (Geisler and Kersten, 2002) embodies the assumption that perception is based on two sources of information: prior beliefs about the state of the world are updated by incoming sensory information; perceptual decisions are then based on the updated beliefs. For the purpose of modeling, the psychological concepts of belief, sensory processing, perception, and decision are mapped onto mathematical concepts derived from probability theory: respectively, these are the prior, the likelihood function, the posterior, and the cost function. Specifically, the observer's belief about the statistical regularities of the world is modeled by a probability distribution (the prior); the observer's noisy sensory processing is reflected in a measurement distribution, which specifies a likelihood function; the combination of prior and likelihood according to Bayes' theorem models the combination of belief and sensory information; this results in an a posteriori probability distribution (the posterior), representing the space on which the perceptual decision is made. One value picked from the domain of this distribution according to an implicit decision rule, determined by gains and losses specified in a cost function, represents the ultimate percept of the observer.