A Model of H-NS Mediated Compaction of Bacterial DNA

Abstract

The histone-like nucleoid structuring protein (H-NS) is a nucleoid-associated protein, which is involved in both gene regulation and DNA compaction. H-NS can bind to DNA in two different ways: in trans, by binding to two separate DNA duplexes, or in cis, by binding to different sites on the same duplex. Based on scanning force microscopy imaging and optical trap-driven unzipping assays, it has recently been suggested that DNA compaction may result from the antagonistic effects of H-NS binding to DNA in trans and cis configurations. To get more insight into the compaction mechanism, we constructed a coarse-grained model description of the compaction of bacterial DNA by H-NS. These simulations highlight the fact that DNA compaction indeed results from the subtle equilibrium between several competing factors, which include the deformation dynamics of the plasmid and the several binding modes of protein dimers to DNA, i.e., dangling configurations, cis- and trans-binding. In particular, the degree of compaction is extremely sensitive to the difference in binding energies of the cis and trans configurations. Our simulations also point out that the conformations of the DNA-protein complexes are significantly different in bulk and in planar conditions, suggesting that conformations observed on mica surfaces may differ significantly from those that prevail in living cells.

Introduction

The chromosomal DNA of bacteria is folded into a compact body, called the nucleoid, which is distinctly different from the rest of the cytoplasm. Bacteria employ a number of nucleoid-associated proteins that influence the organization of the nucleoid by bending, wrapping, or bridging DNA (1–4). In addition, most of these proteins act as global regulators of gene expression (5,6). The histone-like nucleoid structuring protein (H-NS) is a key player in genome organization by forming bridges between DNA duplexes (7,8). Moreover, H-NS is an important global regulator (regulating several hundreds of genes) and may function as an environmental sensor (9,10) that perceives changes in the growth conditions of the bacterium and facilitates physiological changes required for adaptation to the new conditions. H-NS is a small protein (137 residues, 15.5 kDa), which is functional as a dimer. Each monomer is composed of an N-terminal dimerization domain (residues 1–64) (11,12) connected to a C-terminal DNA-binding domain (residues 91–137) (13) through a flexible linker (14). The dimer can bind to DNA in two different ways, namely in trans, by binding to two separate DNA duplexes, and in cis, by binding to different sites on the same duplex (7,8,15,16). The contemporary view reflects that H-NS initially binds to specific nucleotide sequences (13,17), followed by additional H-NS dimers binding to adjacent sites on DNA (14,18).

Despite the enormous effort of many research groups, there are several aspects of H-NS that remain controversial or completely unknown (19). Up to now, a complete, high-resolution structure of full-length H-NS, either free or complexed with DNA, has proven elusive. Structural models for the N-terminal dimerization domain have been determined by NMR spectroscopy (11,12) and x-ray crystallography (18), showing that dimerization occurs through the formation of a coiled-coil interaction motif. However, the degree of oligomerization of H-NS in solution is unclear, because dimers, tetramers, and larger oligomers have been observed under different conditions (11,20–23). An NMR spectroscopy study on the DNA-binding domain revealed that a specific sequence in the domain binds to the minor groove (13). A genome-wide analysis identified a strong correlation between H-NS binding sites and AT-rich regions on the DNA (24), and in addition, a 10-basepair (bp) high-affinity H-NS binding site was also discovered in the proV promoter (25). Still, the specific mechanisms for recognition of these regions by H-NS remain unclear. Furthermore, the mechanism by which an H-NS dimer determines to bind in trans or in cis mode is unknown. By probing H-NS/DNA interactions through equilibrium H-NS-mediated DNA looping scanning-force microscopy imaging and dynamic optical trap-driven unzipping assays, Wiggins et al. (15) suggested that observed DNA loops may result from the antagonistic effects of trans- and cis-binding.

Molecular simulations can complement experiments by providing details at high spatial and temporal resolution. For example, coarse-grained Monte Carlo simulations recently indicated that H-NS bridge formation occurs preferentially at planar bends in the DNA (26). In this article, we aim to shed additional light on the H-NS mediated compaction of DNA by using a Hamiltonian coarse-grained model for H-NS binding to DNA. Such models have proven to be very helpful in understanding facilitated diffusion, i.e., the various mechanisms by which proteins scan DNA sequences while searching for their target site (27–29). In this model, trans- and cis-binding are not introduced a priori, but follow instead from the explicit interaction energy function between DNA and the proteins. The results presented in this article highlight the fact that DNA compaction is indeed driven by the subtle equilibrium between several competing factors, including the deformation dynamics of the plasmid and the several binding modes of protein dimers to DNA. Moreover, simulations of DNA constrained to a planar system suggest that the conformations of DNA/H-NS complexes deposited on mica surfaces may differ substantially from those that prevail in living cells.

Methods

Construction of the coarse-grained model was aimed at mimicking the DNA/H-NS incubation conditions used by Dame et al. (7). The Supporting Material gives a detailed description of the model. In brief, it consists of a pUC19 plasmid and 224 H-NS dimers (i.e., 1 dimer:12 bp, as in Dame et al. (7)) at a temperature of T = 298 K (1 k_BT ≈ 2.48 kJ/mol) enclosed in a sphere of radius R₀ = 0.434 μm or a half-sphere of radius R₀ = 0.547 μm. As in previous work (27–30), DNA is modeled as a chain of beads, where each bead represents 15 DNA basepairs (bp). This level of coarse-graining is reasonable, because studies have shown that an H-NS DNA-binding domain occupies ∼15 bp (31). As a consequence, the 2686-bp pUC19 plasmid is modeled as a cyclic chain of 179 beads. To keep the same level of coarse-graining, H-NS dimers are modeled as chains of three beads. The chosen equilibrium distance between two successive beads (L₀ = 7.0 nm) corresponds to the two N-terminal domains of H-NS dimers being arranged in anti-parallel (12) rather than in parallel (11) geometries. Electric charges are placed at the center of each bead ($-12\overline{e}$ on DNA beads, $4\overline{e}$ on H-NS terminal beads, and $-8\overline{e}$ on H-NS central beads, where $\overline{e}$ denotes the absolute charge of the electron) and the DNA molecule and the H-NS dimers interact through the sum of electrostatic terms (Debye-Hückel potentials) and excluded volume terms. The parameter χ of the excluded volume terms was chosen such that the computed enthalpy change upon a single H-NS molecule binding to DNA matches the experimental value at T = 298 K (31). For a dimer binding to DNA, the computed enthalpy change is ΔH = 11.1 k_BT (see Fig. S1 in the Supporting Material), and the enthalpy change of an H-NS dimer binding two DNA sites in the trans configuration is twice this value, 22.2 k_BT. Because at equilibrium H-NS dimers are assumed to be linear, the enthalpy change of an H-NS dimer binding two DNA sites in the cis mode depends on its bending rigidity G. We performed simulations with two different values of G, namely G = 2 k_BT and G = 4 k_BT, which correspond to cis-binding enthalpy changes of 19.2 k_BT (see Fig. S2) and 16.8 k_BT (see Fig. S3), respectively.

The dynamics of the system was investigated by numerically integrating the Langevin equations of motion for 10 ms with a time step of 20 ps. Two different sets of simulations were performed. The first set of simulations, hereafter labeled 3D, aimed at mimicking the motion of the system in bulk buffer by allowing all molecules to move freely inside the sphere. The second set of simulations, hereafter labeled 2D, aimed at mimicking DNA molecules deposited on cleaved mica surfaces by restricting the motion of H-NS dimers to a half-sphere, and constraining the plasmid to remain in the neighborhood of the limiting disk. Four 2D simulations were run for each value of G starting from circular plasmid conformations and eight 3D simulations were run for each value of G starting from thermalized plasmid conformations. Analysis of the simulations consisted in counting every 10 μs the number of bound H-NS dimers. An H-NS dimer was considered bound to DNA if at least one bead was within a distance of 2 nm from a DNA bead (see the Supporting Material and Fig. S4 for a discussion on the choice of 2 nm for the distance threshold). Also, the nature of the bound H-NS dimers was tracked. A dimer was considered to be bound in cis if the two terminal beads were interacting with DNA beads separated by at most two DNA beads. If instead, the H-NS dimer was interacting with two DNA beads separated by (strictly) more than two DNA beads, the H-NS/DNA interaction was counted as a trans bond. Finally, the dimer was considered to be dangling, if only one bead of the dimer was interacting with the DNA. Furthermore, the radius of gyration of the plasmid, i.e., the square-root of the trace of its gyration tensor, was also computed every 10 μs.

Results and Discussion

As described in Methods, the model consists of a cyclic DNA molecule with 179 binding sites and 224 H-NS dimers, which move under the action of thermal noise and interaction forces, enclosed in a sphere. When an H-NS dimer comes close to a free DNA site, binding can occur between this DNA bead and a terminal bead in the H-NS dimer, due to the electrostatic attraction between the positive charge placed on the H-NS terminal beads and the negative charge placed on the DNA bead. Subsequently, the other, dangling bead of the H-NS dimer can bind to another site on the DNA. If the second site is within three beads of the first one, the H-NS dimer has bound in cis mode. Alternatively, the second binding site can be located far away from the first site from a sequence point of view, resulting in an H-NS dimer bound in trans. All bonds between H-NS and DNA are reversible, which means that a twice-bound H-NS dimer can return to the dangling configuration and that a dangling H-NS can detach from DNA or slide along the sequence. As only trans-binding dimers contribute to DNA compaction (cis-binding and dangling dimers contribute to DNA stiffening (16)), the number of trans-binding H-NS dimers is the key quantity to measure DNA compaction. In contrast, cis-binding dimers tend to render the DNA inactive, as they prevent binding sites from participating in DNA compaction. The dangling dimers have a more versatile role. Even though they do not contribute to compaction at the current timestep, their probability to form a trans-binding dimer at later timesteps may be high.

The motion of DNA plays a significant role in the global dynamics of H-NS dimers in the presence of DNA. The simulations show that thermal noise, introduced by the Langevin equations of motion, is sufficient to severely deform the cyclic plasmid chain, allowing for two sites, widely separated in sequence, to eventually come close in space. Upon two sequentially distant sites approaching each other, one of three events may occur:

• 1.If no H-NS dimer is bound, the sites will again move apart after a short while.
• 2.If both sites contain a cis-binding or dangling H-NS dimer, both sites will also move apart again.
• 3.In the case of one free site and one site occupied by a dangling H-NS dimer approaching each other, trans-binding can occur.

A single trans-binding bridge is not very strong by itself and is likely to be broken by further deformation of the plasmid chain due to thermal noise. Nevertheless, a single trans-bound dimer keeps the two sites in close vicinity for a substantially longer time. As a consequence, additional trans-binding bridges are more likely to form at sites close to the first trans-binding dimer, provided that other pairs of free and dangling dimer sites are available. Therefore, under suitable conditions (7) the first trans-binding dimer can act as a seed to propagate compaction, a mechanism sometimes referred to as cooperativity.

The effect of the H-NS dimer cis-binding energy on DNA compaction

Because there are many interacting possibilities at each step, the final state of the system will be very sensitive to small changes in the description of the interactions. To begin, we investigated the effect of changing the cis interaction energy. This energy depends on the bending rigidity G. At higher values of G, the H-NS dimer is stiffer and less likely to bend. Therefore, we expect that at higher values of G, fewer H-NS dimers will bind in cis mode, because bending of the H-NS molecule is required for cis-binding. We performed three-dimensional simulations for G = 2 k_BT and G = 4 k_BT, which correspond to cis-binding enthalpy differences ΔH of 19.2 k_BT and 16.8 k_BT, respectively. Fig. 1 shows the time evolution of the number of H-NS dimers bound to DNA for G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot), partitioned in dangling dimers, cis- and trans-binding dimers. For both values of G, the average number of dangling proteins is comparable, tending toward a value close to 50 at long times. In contrast, there is a huge difference in the number of cis-binding dimers. Indeed, for G = 2 k_BT the average number of cis-binding dimers tends toward 25 or 30 at long times, while this number remains very small, close to 5, for G = 4 k_BT. Conversely, the number of trans-binding dimers at long times is close to 5 and 25 for G = 2 k_BT and G = 4 k_BT, respectively. This indicates that the moderate difference in the value of the cis-binding energy is sufficient to induce large changes in the average number of cis- and trans-binding dimers. In contrast, the time evolution of the fraction of DNA sites occupied by H-NS dimers, shown in Fig. S5, indicates that the value of G has little effect on the occupation of DNA sites by H-NS. Indeed, the fraction of occupied sites after 10 ms is close to 0.65 for both values of G.

Figure 1.

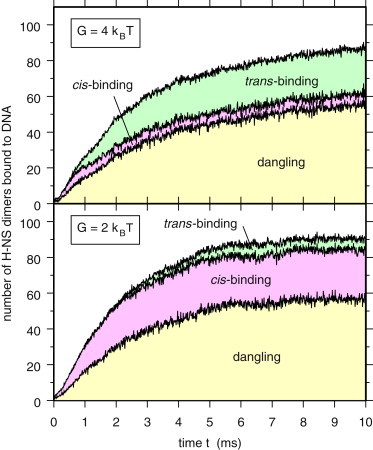
Time evolution of the number of H-NS dimers bound to DNA (3D simulations). Area charts showing the time evolution of the number of H-NS dimers bound to DNA, and the partitioning into dangling dimers and cis- and trans-binding dimers, for 3D simulations with G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot). The system consists of 224 H-NS dimers and one plasmid with 179 binding sites. Results were averaged over eight different trajectories starting from thermalized plasmid conformations.

The huge difference in the number of cis- and trans-binding dimers for the two different bending rigidities has profound effects on the dynamics of the condensed plasmid, as illustrated in Fig. 2. This figure shows the occupation of DNA sites by trans-binding H-NS dimers, which contribute to compaction, for G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot). At G = 4 k_BT, the large number of trans-binding dimers facilitates many bridges between DNA sites located everywhere in the sequence. As a result, the plasmid molecule acquires a globular shape, which changes little with time, as demonstrated by the almost constant value of its radius of gyration, plotted in Fig. 3 for a single simulation and in the top plot of Fig. S6 for eight different simulations. In contrast, for G = 2 k_BT, the small number of trans-binding H-NS dimers allows for only a few, short-lived bridges, which form and break with fluctuations in the plasmid conformation (see Fig. 2). As a consequence, the plasmid molecule displays a very rich dynamics, with compact shapes following more loosely packed conformations and vice versa. This behavior is again clearly reflected in the time evolution of the radius of gyration of the plasmid, shown in Fig. 3 for a single simulation and in the bottom plot of Fig. S6 for eight different simulations. Movie S1 and Movie S2 in the Supporting Material, showing the time evolution of the plasmid conformations for the simulations also shown in Figs. 2 and 3, clearly illustrate the differences in the plasmid dynamics.

Figure 2.

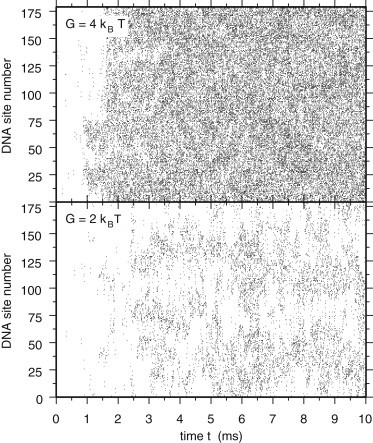
Time evolution of bridged DNA sites (3D simulations). Diagrams showing the time evolution of bridged DNA sites for single 3D simulations with G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot). DNA sites are numbered from 1 to 179 and reported on the vertical axis. Every 10 μs, the DNA sites occupied by a trans-binding H-NS dimer are listed and ticks are placed in the diagram at the corresponding locations.

Figure 3.

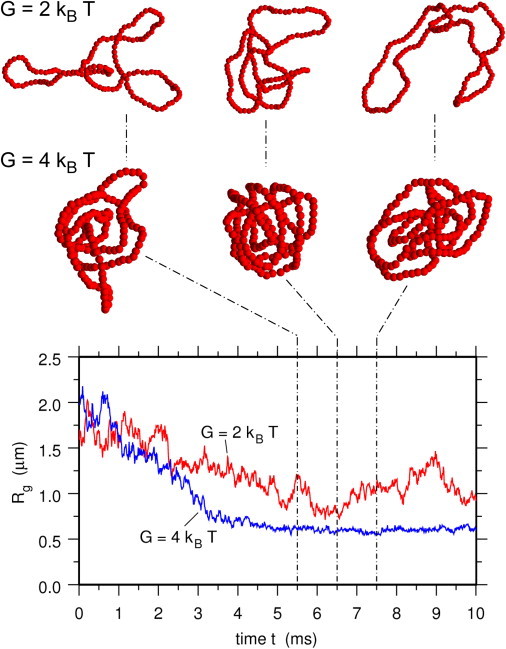
Time evolution of the radius of gyration of the plasmid molecule (3D simulations). (Bottom plot) Time evolution of the radius of gyration of the plasmid molecule for single simulations with G = 2 k_BT and G = 4 k_BT. (Insets above plot) Conformations of the plasmid molecule at t = 5.5 ms, 6.5 ms, and 7.5 ms for G = 2 k_BT (top row) and G = 4 k_BT (second row). H-NS dimers are not shown for clarity.

A comparison of H-NS mediated compaction in bulk and on a surface

The simulations discussed above mimicked bulk solution conditions. However, in the scanning force microscopy imaging experiments of Dame et al. (7), solutions containing DNA/H-NS complexes were deposited on freshly cleaved mica surfaces followed by gentle drying of the mica disks. Deposition on a surface plate may significantly alter the conformations displayed by naked DNA in comparison to the bulk solution situation (32). Magnesium ions mediate the binding of DNA to mica, by forming bridges between the negative charges on the phosphate backbone and the negatively charged mica sites. These bridges are strong, because DNA molecules do not return into the solution after deposition onto the surface under standard conditions (32). Moreover, when deposited on untreated freshly cleaved mica, DNA molecules equilibrate onto the surface as in an ideal 2D solution, while the conformations of DNA molecules deposited on glow-discharged or H⁺-exchanged mica resemble the projection of the bulk 3D conformations onto a 2D plane (32). The latter results from increasing the interaction energy between DNA and the surface by discharging, soaking, or rinsing the mica plate with deionized water, which displaces the metal ions. These stronger binding energies prevent lateral diffusion and equilibration of the DNA molecule.

To our knowledge, the deposition of DNA/H-NS complexes on mica surfaces has not been studied in such detail. It is, however, interesting to note that Dame et al. (7) deposited the complexes on freshly cleaved surfaces without prior treatment, representing conditions where naked DNA would equilibrate as in an ideal 2D solution. We therefore investigated the effects of constraining the DNA plasmid to remain close to a plane (see Methods and the Supporting Material for more detail on these calculations). Constraining DNA to move in 2D rather than in 3D has a huge impact on the elastic bending energy, the apparent rigidity of the molecule, the number of cis- and trans-bonds that can be formed, and therefore on the whole compaction dynamics. Fig. 4 shows the time evolution of the number of H-NS dimers bound to DNA obtained from 2D simulations with G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot), including the partitioning in dangling dimers and cis- and trans-binding dimers. Comparison of 2D and 3D simulations indicates that the general trends observed in 3D are preserved in 2D, in particular the swapping of the numbers of cis- and trans-binding H-NS dimers when switching from G = 4 k_BT to G = 2 k_BT. However, the number of trans-binding dimers is substantially smaller in 2D than in 3D for both values of G. For G = 2 k_BT, this number has become so small that it cannot be distinguished anymore in the bottom plot of Fig. 4. When looking at the degree of compaction, measured by the number of DNA sites occupied by trans-binding H-NS dimers, it is clear that compaction hardly takes place in 2D for G = 2 k_BT (bottom plot of Fig. 5), while it is rapid and quite homogeneous for G = 4 k_BT (top plot of Fig. 5).

Figure 4.

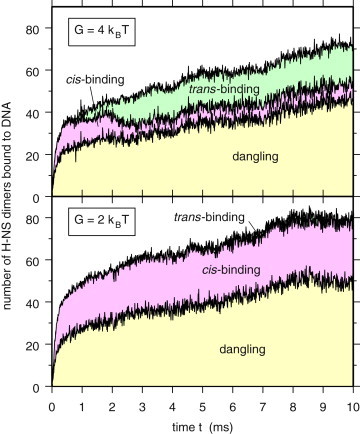
Time evolution of the number of H-NS dimers bound to DNA (2D simulations). Area charts showing the time evolution of the number of H-NS dimers bound to DNA, and the partitioning into dangling dimers and cis- and trans-binding dimers, for 2D simulations with G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot). The system consists of 224 H-NS dimers and one plasmid with 179 binding sites. Results were averaged over four different trajectories starting from circular plasmid conformations.

Figure 5.

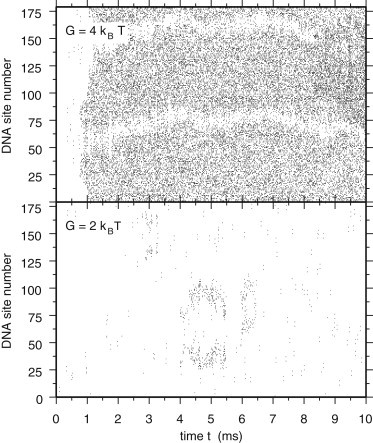
Time evolution of bridged DNA sites (2D simulations). Diagrams showing the time evolution of bridged DNA sites for single 2D simulations with G = 2 k_BT (bottom plot) and G = 4 k_BT (top plot). DNA sites are numbered from 1 to 179 and reported on the vertical axis. Every 10 μs, the DNA sites occupied by a trans-binding H-NS dimer are listed and ticks are placed in the diagram at the corresponding locations.

The differences between condensed conformations in 2D and 3D are even more striking. For G = 4 k_BT, condensed planar plasmid molecules resemble coil-shaped filaments, caused by the many parallel trans-binding H-NS dimers (see Fig. 6), whereas in 3D they adopt a more globular shape (see the snapshots in Fig. 3 and see Movie S1). Similarly, for G = 2 k_BT the (eventually) condensed planar plasmids consist of open loops connected by bridges (see Fig. 6), which differ markedly from the more intricate conformations observed in 3D (see the snapshots in Fig. 3 and see Movie S2). Interestingly, the condensed conformations computed in 2D for G = 2 k_BT are quite similar to those observed by Dame et al., who reported that open end-loops are present on all observed DNA/H-NS complexes (7). It is therefore tempting to conclude that the correct value for G, i.e., the one that correctly predicts the experimental compaction results, is G = 2 k_BT. However, this conclusion is premature because the reproducible observation of open end-loops may merely reflect the higher affinity of the mica surface for complexes with open DNA end-loops than for completely condensed DNA molecules (7). Stated in other words, if coil-shaped filaments detach preferentially from the surface during rinsing, then one would observe only complexes with open end-loops during scanning force microscopy experiments, even if coil-shaped filaments had also formed during the equilibration phase. Simulations with a more realistic description of the interactions between DNA and the surface, thus facilitating a comparison between the surface binding strengths of coiled versus open end-looped conformations, would therefore be of great interest in obtaining a firm estimate for the value of G.

Figure 6.

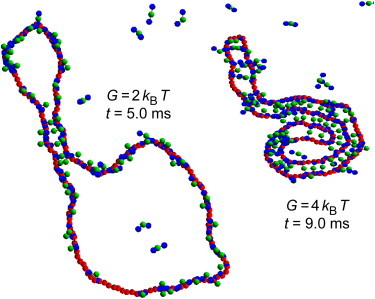
Typical 2D plasmid conformations. Typical conformations of the plasmid for the trajectories shown in Fig. 5. Snapshots were taken at t = 5.0 ms (for G = 2 k_BT) and t = 9.0 ms (for G = 4 k_BT), respectively.

Nevertheless, the results of the 2D simulations agree much better with experimentally observed condensed complexes than those of the 3D simulations. This suggests that relaxation of the DNA/H-NS complexes on a mica surface strongly affects their geometry and that the conformations observed in the course of AFM experiments may consequently not be the mere projections of bulk conformations on the surface, but may instead differ significantly from those that prevail in living cells.

Conclusion

In this work, we have constructed a coarse-grained model description of the compaction of bacterial DNA by H-NS proteins. The level of coarse-graining of the model is sufficiently high to allow for the numerical integration of trajectories for 10 ms but fine enough to match the experimental observation that each bound H-NS molecule occupies ∼15 bp. Results of the simulations highlight the fact that DNA compaction is driven by the subtle equilibrium among several competing factors, including the deformation dynamics of the plasmid and the several binding modes of protein dimers, i.e., dangling configuration and cis- and trans-binding. In particular, the simulations showed that condensed DNA conformations are very sensitive to the binding energy difference between the cis- and trans-binding conformations. If H-NS cis-binding dimers are not substantially less stable than trans-binding dimers, then cis-binding and dangling dimers occupy most of DNA binding sites, and the number of trans-binding dimers, equal to the number of bridges between two DNA sites that are at least three beads apart, remains small. This leads to moderately condensed DNA conformations, which are still able to deform strongly. In contrast, if cis-binding dimers are substantially less stable than the trans-binding ones, then the number of trans-binding proteins becomes large, resulting in DNA rapidly acquiring a globular conformation, which changes little in time. Our simulations also pointed out that the conformations of DNA/H-NS complexes are significantly different in 2D and in 3D. This observation suggests that the relaxation of complexes on a mica surface has a strong influence on the observed conformations and, consequently, that conformations observed on mica plates may differ from those that prevail in living cells.

There are several lines along which the model described in this work can be extended and improved.

First of all, a more realistic description of the interactions between the plasmid and the mica surface would be of great interest to confirm that the conformations observed during scanning force microscopy experiments indeed result from the equilibration of globular bulk conformations on the mica surface. To this end, one should first construct a suitable interaction term between DNA and the surface, which would lead to correct predictions for the dynamics of naked DNA deposition, in particular regarding the complete relaxation of DNA at low surface charge density and the freezing of lateral motion at higher charge density. By using this interaction potential for DNA/H-NS complexes, the simulations can shed light on whether H-NS bridges are sufficient to prevent equilibration or if the bridges that exist before deposition break and/or reorganize during deposition and equilibration.

A straightforward extension of this work consists of performing similar simulations close to in vivo conditions, instead of the experimental conditions of Dame et al. (7). As a necessary benchmark to adjust the parameters of the model, the simulations reported in this article were indeed performed with one 2686 bp plasmid and 224 H-NS dimers to allow for comparison with experiments. In contrast, bacterial DNA may be several million basepairs long and each cell contains approximately one H-NS dimer per 200 DNA basepairs, instead of one H-NS dimer per 12 DNA basepairs as in the experiment by Dame et al. (7). Performing simulations in in vivo conditions could provide interesting information, such as, for example, an estimation of the compaction factor due to H-NS, but will also certainly be very expensive from the computational point of view.

Yet another step closer to simulating the actual bacterial genome would involve including additional different proteins, known to play an important role in the compaction of bacterial DNA, such as HU, IHF, StpA, Dps, or FIS. StpA, which is homologous to H-NS, is also able to form bridges between two separate DNA duplexes (33). During the stationary phase, Dps binds to chromosomal DNA, thereby forming a stable complex called a biocrystal, but the mode of the DNA/Dps interaction is not yet fully understood (34). Fis induces compaction of DNA essentially due to bending (35). At last, HU and IHF, which are homologous to each other, condense DNA by bending and undertwisting it (36). Introducing all these different proteins into a single model is a formidable task, but one could, as a first step, investigate the essential properties of each of them by using a similar mesoscopic model as used here for H-NS.