Effects of cochlear loading on the motility of active outer hair cells

Abstract

Outer hair cells (OHCs) power the amplification of sound-induced vibrations in the mammalian inner ear through an active process that involves hair-bundle motility and somatic motility. It is unclear, though, how either mechanism can be effective at high frequencies, especially when OHCs are mechanically loaded by other structures in the cochlea. We address this issue by developing a model of an active OHC on the basis of observations from isolated cells, then we use the model to predict the response of an active OHC in the intact cochlea. We find that active hair-bundle motility amplifies the receptor potential that drives somatic motility. Inertial loading of a hair bundle by the tectorial membrane reduces the bundle’s reactive load, allowing the OHC’s active motility to influence the motion of the cochlear partition. The system exhibits enhanced sensitivity and tuning only when it operates near a dynamical instability, a Hopf bifurcation. This analysis clarifies the roles of cochlear structures and shows how the two mechanisms of motility function synergistically to create the cochlear amplifier. The results suggest that somatic motility evolved to enhance a preexisting amplifier based on active hair-bundle motility, thus allowing mammals to hear high-frequency sounds.

Our ears are amazing signal detectors that reconcile great sensitivity with an enormous dynamic range. The faintest sounds that we can hear vibrate our eardrums by less than 1 pm and are a trillion times less intense than the loudest sounds that we can tolerate (1, 2). We can distinguish pure tones that differ in frequency by less than 0.2%, yet the frequency range of our ears exceeds a thousandfold (2). These features are all the more remarkable given that the mechanoreceptive organ of Corti operates in liquid and is therefore highly damped (3).

An active process enhances the performance of the mammalian ear by augmenting sound-induced vibrations in the cochlea (2–6). This process results from the action of specialized outer hair cells (OHCs) whose motility boosts the motion of the cochlea in response to sounds, thus amplifying the signal transmitted to the brain. These cells counteract the damping that would otherwise limit the cochlea’s sensitivity and frequency discrimination (3, 7). OHCs exhibit two forms of mechanical activity, hair-bundle motility and somatic motility, which may both contribute to the cochlear amplifier.

Named for the mechanosensitive hair bundles protruding from their apices, hair cells transduce vibrations of their bundles into an electrical response. Cochlear hair cells are housed in the cochlear partition, which includes the organ of Corti sandwiched between the tectorial and basilar membranes (Fig. 1A). The hair bundle of each OHC is connected at its tip to the acellular tectorial membrane, and the soma of each OHC is linked to the basilar membrane through a rigid Deiters’ cell (8). These membranes mechanically load each OHC with mass, damping, and stiffness.

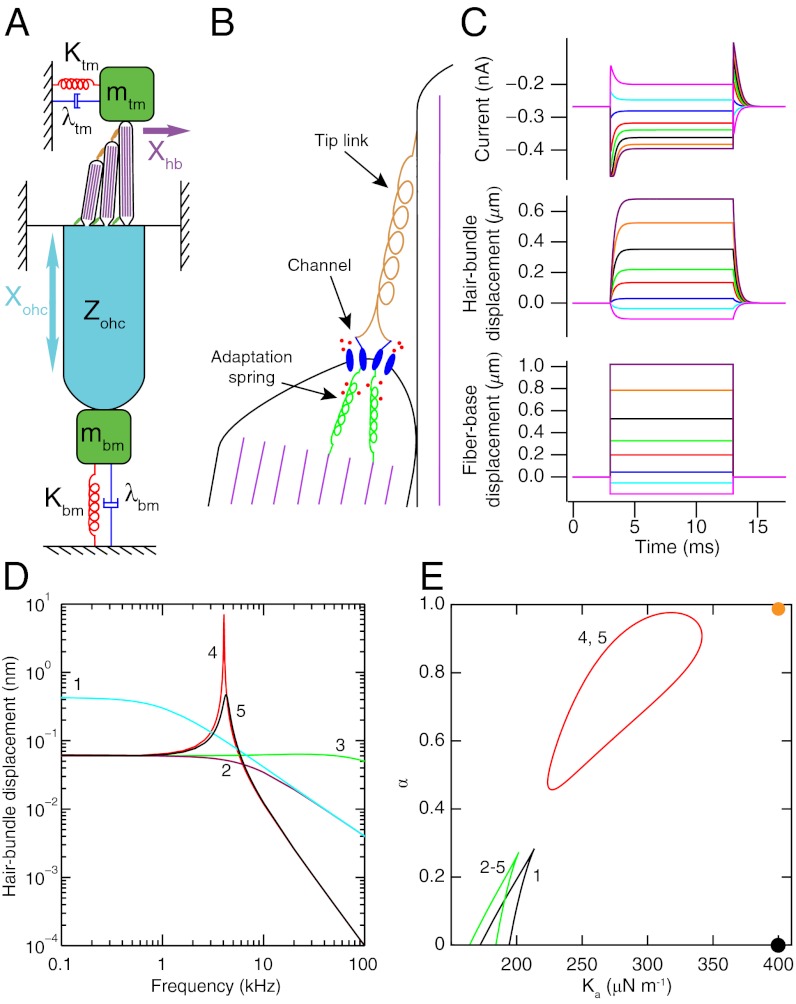
Fig. 1.

(A) A schematic drawing portrays an OHC and the associated cochlear structures that provide its mechanical loads. The hair bundle has three rows of stereocilia with progressively increasing heights. Filled with filamentous actin (purple), each stereocilium pivots about its base and is connected to its tallest neighbor through a tip link (orange). The bundle is loaded by the mass m_tm, damping λ_tm, and stiffness K_tm associated with the tectorial membrane. The soma of the OHC confronts the mass m_bm, damping λ_bm, and stiffness K_bm of the basilar membrane. The mechanical impedance Z_ohc of the soma is described in Fig. 2A. The hair bundle’s displacement X_hb and the soma’s extension X_ohc are indicated by arrows. (B) Adjacent stereocilia within a hair bundle are connected by a tip link at the lower end of which are thought to reside two mechanically gated cation channels. Ca²⁺ (red circles) enters the stereocilium through the channels and binds to the adaptation springs connecting the channels to the actin cytoskeleton (purple), thereby reducing their stiffness. The deformation of the membrane at the tip of the shorter stereocilium by the tension in the tip link is known as tenting. (C) Step displacements of the base of a flexible fiber attached atop the hair bundle of an active 4-kHz hair cell evoke a simulated hair-bundle displacement and transduction current. (D) The hair bundle’s simulated response to sinusoidal stimulation 13 pN in amplitude is shown under different conditions (SI Appendix, Table S1). (1) The active hair bundle is loaded by a fiber’s stiffness K_f and damping λ_f. (2) The stiffness of the load is increased to equal the effective stiffnesses of the tectorial membrane and basilar membrane K_tm. (3) The load’s damping λ_tm is given a negative value to capture the effect of somatic feedback. (4) The mass m_tm of the tectorial membrane is added. (5) Hair-bundle activity is removed by reducing the Ca²⁺ sensitivity α. (E) A state diagram, parameterized by α and the adaptation springs’ maximal stiffness K_a, describes the bundle dynamics associated with the various conditions enumerated above. Wedge-shaped regions of bistability are demarcated by lines of fold bifurcations. Inside the region enclosed by a red line of Hopf bifurcations the hair bundle oscillates spontaneously; elsewhere the bundle is monostable. The orange and black circles denote the operating points for an active and a passive hair bundle, respectively.

Hair bundles produce a variety of active movements including spontaneous oscillations (9). The significance of active hair-bundle motility in mammals is uncertain, however: Hair bundles do not seem to be well positioned to apply forces that amplify the movements of the basilar membrane (5, 10). Moreover, only low-frequency spontaneous oscillations have been observed in nonmammals. Finally, inasmuch as the mechanical properties of experimental probes restrict the speed at which hair bundles respond in experiments (11), the organ of Corti and associated structures in contact with each OHC might likewise limit the response rate in an intact cochlea (12).

Somatic motility, also known as electromotility, is the capacity of OHCs to alter the length of their cell bodies in response to a change in membrane potential (13). These length changes are as great as 5% in isolated cells, operate to frequencies exceeding 80 kHz, and are required for sensitive hearing (14, 15). The extent of somatic motility in the cochlea is limited, however, by the mechanical load imposed by surrounding structures (16). Furthermore, the receptor potential that drives electromotility suffers severe attenuation at high frequencies by the resistance and capacitance of the OHC’s membrane, an issue known as the RC time-constant problem (14, 17). It therefore remains unclear how somatic motility can augment the motion of the cochlea at high frequencies.

Although models have been developed to incorporate both types of motility (18–21), their complexity obfuscates how an active OHC can influence the motion of structures that are much stiffer, more damped, and more massive than the cell itself. In this paper, we attempt to bridge this gap by using experimental data to construct a simple model OHC with physiologically realistic properties for a high-frequency location in the cochlea. We then use the model to examine the effects of coupling an active OHC to structures with the mass, damping, and stiffness found in the actual cochlea.

To distinguish the effects of hair-bundle motility from those of somatic motility we hold the apical surface of the OHC in a fixed position and consider each form of motility separately before analyzing how these processes interact with one another to amplify the motion of the cochlear partition. Because the apex of the OHC is prevented from moving in this model, the hair bundle cannot apply forces on the basilar membrane. Nonetheless, we find that active hair-bundle motility amplifies the transduction current and can thus influence the basilar membrane by enhancing the receptor potential that drives somatic motility.

Results

Active Hair-Bundle Motility.

The hair bundle comprises dozens to hundreds of actin-packed tubular processes, the stereocilia, that protrude from a hair cell’s apex (9) (Fig. 1A). Each stereocilium is connected to its tallest neighbor by a proteinaceous tip link at whose lower end are thought to lie two mechanoelectrical-transduction channels (Fig. 1B) (22). Increased tension in the tip link as a result of hair-bundle deflection promotes opening of these channels and thus initiates a transduction current.

Active hair-bundle motility stems from a Ca²⁺-dependent adaptation process that alters the channel’s open probability during bundle displacement (9). Adaptation manifests itself most clearly through a decline in the transduction current during the application of a force step in the positive direction, toward the bundle’s tall edge. Two adaptation mechanisms are thought to exist, corresponding to the short and long time scales associated with this decrease in current.

The machinery for fast adaptation must be in close proximity to the transduction channels so that the speed of adaptation is not unduly limited by the diffusion of Ca²⁺ (23). We accordingly introduce a model for fast adaptation at the base of each tip link, the probable location of the transduction channels (22). The model accords with the observation that the membrane of a stereociliary tip is sometimes observed to bulge outward, or “tent,” at the site of the tip link’s insertion (24), which may reflect the extension of an intracellular element in series with the tip link (Fig. 1B). We propose that each channel is anchored to the stereociliary cytoskeleton by a viscoelastic connection whose stiffness decreases dynamically as the local Ca²⁺ concentration grows. An influx of Ca²⁺ thus causes the channel to reclose as the adaptation spring extends owing to its increased compliance. This mechanism could easily be quick enough to account for fast adaptation.

The hair-bundle displacement X_hb and the adaptation-spring extension X_a are described by two nonlinear, coupled differential equations (SI Appendix, section 1). The activity of the bundle reflects the force in the adaptation springs,

in which K_a is the springs’ maximal stiffness and X_r is their reference length. If the adaptation springs lie sufficiently close to the transduction channels then the local Ca²⁺ concentration is proportional to the channels’ open probability P_o (23); α is then the dimensionless sensitivity of channel opening. The hair bundle’s activity is maintained by three energy sources: the endocochlear potential, the OHC’s resting potential, and the Ca²⁺ gradient across the stereociliary membrane (SI Appendix, section 2). Because these sources of energy determine K_a and α, altering either of these two parameter values adjusts the level of bundle activity.

The nonlinearity of the hair bundle arises from the dependence of P_o upon X_hb, which is described by a Boltzmann function (9). We find that the observed sensitivity of P_o to changes in X_hb (25) may have been underestimated, however, for fast adaptation alters P_o during measurements with current techniques (SI Appendix, section 3).

The adaptation-spring model reproduces the responses of hair bundles to step stimulation with a glass fiber, in particular those from the 4-kHz place in the cochlea that has been examined experimentally (Fig. 1C) (11). The values of four parameters, including K_a and α, are chosen such that the maximal and steady-state transduction currents and displacements agree with experimental observations. Other hair-bundle properties are selected to agree with independent measurements (SI Appendix, Table S1).

A radial segment of the basilar membrane one OHC in width experiences a force with an amplitude of 13 pN during sinusoidal stimulation at a sound-pressure level of 30 dB. We can use the model to predict a hair bundle’s response under various loading conditions to forcing of this magnitude (Fig. 1D). When the hair bundle is loaded by a fiber, it acts as a low-pass filter with a cutoff frequency of about 1 kHz. The operating point of the system lies in the monostable part of the bundle’s state diagram, far from any bifurcation (Fig. 1E). Adding a stiffness load equal to that of the tectorial membrane reduces the low-frequency response by a factor of 7 and increases the cutoff frequency to about 7 kHz, but the response declines at the 4-kHz characteristic frequency. It has been proposed that somatic motility produces a feedback force on the hair bundle that decreases its damping (19). Although we find that reducing the bundle’s damping increases the cutoff frequency beyond 100 kHz, this change has little effect on the motion at 4 kHz.

Adding to the hair bundle’s load a mass similar to that of the tectorial membrane has a striking effect: A sharply tuned resonance appears at 4.1 kHz, increasing the response at that frequency by more than two orders of magnitude (Fig. 1D). Simultaneously, a set of operating points appears in the bundle’s state diagram at which the bundle oscillates spontaneously. The boundary between this region and the surrounding quiescent points is known as a line of Hopf bifurcations (Fig. 1E). Tuning is sharp and the response is large when the system operates near such a bifurcation (23). The maximal response of the hair bundle decreases by an order of magnitude if the bundle’s activity is eliminated by setting α = 0, thus distancing the operating point from the Hopf bifurcations.

The resonant frequency f_r of the loaded hair bundle depends on both the passive load and the active properties of the bundle (SI Appendix, section 4). If the system behaved like a damped harmonic oscillator then the resonant frequency would be proportional to the square root of the system’s stiffness (SI Appendix, Eq. S12). The resonant frequency of the active system with a low mass is instead directly proportional to the stiffness. This result implies that the gradient in characteristic frequency along the cochlea depends on the active process (12, 19) and indicates why the measured ranges of the cochlea’s passive properties are insufficient to explain its full frequency range (26).

Somatic Motility.

The basolateral surface of an OHC has a unique three-layered structure (27). The plasma membrane bears several million molecules of prestin, the protein responsible for somatic motility. Beneath this lies a cortical lattice consisting of a regular network of actin and spectrin filaments connected to the membrane by pillars. Finally, subsurface cisternae form one or more layers beneath the cortex.

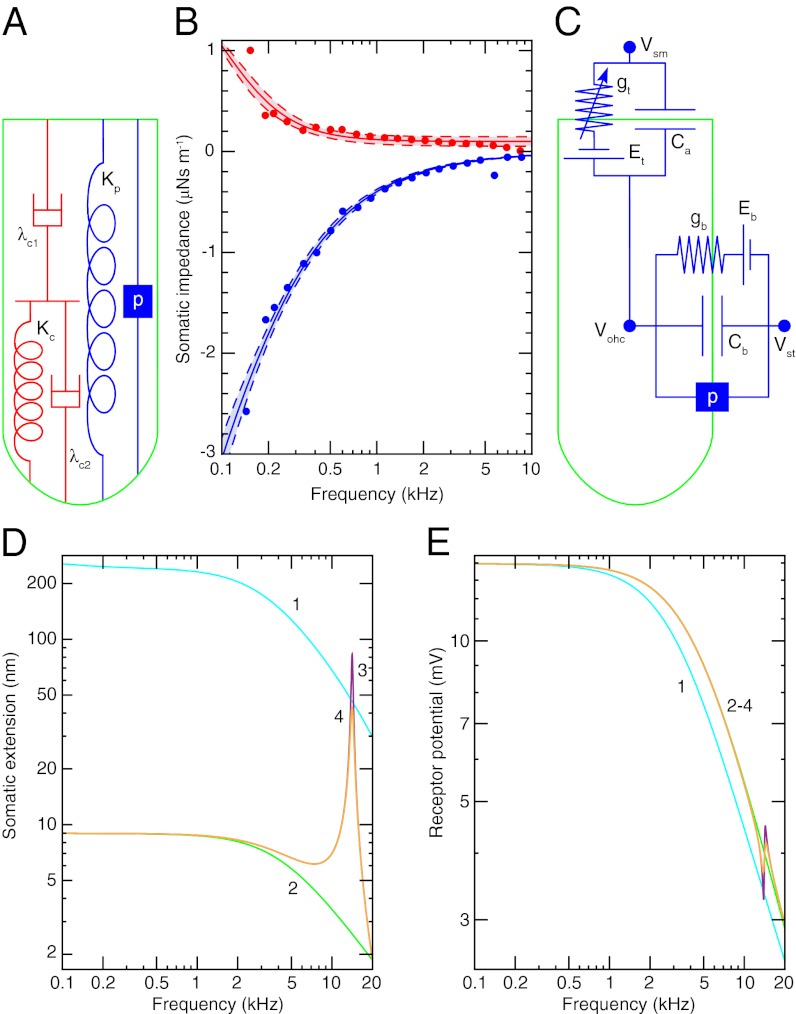
Somatic motility occurs when prestin undergoes a conformational change in response to alterations in the membrane potential (28). The impedance Z_ohc of an OHC from the 14-kHz place in response to sinusoidal forcing at frequencies up to 10 kHz has been measured after the application of anthracene-9-carboxylic acid (9AC) (29), which apparently reduces the stiffness of OHCs without affecting their damping (30). To explain the impedance measurements, we propose a simple mechanical model of the basolateral surface (Fig. 2A) (SI Appendix, section 5). The model comprises two dashpots and two springs and fits the experimental observations well when the springs have the same stiffness (Fig. 2B). The real part of Z_ohc, which corresponds to damping by the OHC, decreases as a function of frequency to about 100 nN⋅s⋅m⁻¹ at 10 kHz. The damping at high frequencies thus resembles the drag on a sphere of the same diameter as the cell.

Fig. 2.

(A) The cortical lattice and subsurface cisternae of an OHC are described by the two dashpots λ_c1 and λ_c2 and the spring K_c. The plasma membrane is represented by a spring K_p in parallel with a piezoelectric element p betokening the prestin molecules. (B) The experimentally determined real part (red circles) and imaginary part (blue circles) of the mechanical impedance of a 14-kHz OHC are simultaneously fit by the model depicted in A with the constraints of no electromotility, 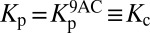, and p = 0 (R² > 0.98, solid lines). The fit yields K_c = 1.32 ± 0.04 mN⋅m⁻¹ (P value < 10⁻²⁸), λ_c1 = 2.00 ± 0.28 μN⋅s⋅m⁻¹ (P value < 10⁻⁷), and λ_c2 = 104 ± 25 nN⋅s⋅m⁻¹ (P value < 0.001). The dashed lines represent 95% confidence intervals. (C) The transduction current flowing across the apical membrane of the OHC responds to changes in the potential difference between the hair cell’s interior and the scala media, V_ohc − V_sm. The potentials of the scala media V_sm at the OHC’s apical surface and of the scala tympani V_st at the OHC’s basolateral membrane are approximately constant. The apical membrane acts as a capacitor C_a in parallel with a variable conductance g_t that represents the transduction channels and has a reversal potential E_t. Driven by the reversal potential of the basolateral somatic membrane E_b, current exits the OHC through its basolateral membrane, which is described by a conductance g_b in parallel with a capacitor C_b and a piezoelectric element p. (D) The model predicts the change in somatic length of a 14-kHz OHC in response to sinusoidal changes in hair-bundle conductance of maximal amplitude around the reference value (SI Appendix, Table S1). Four conditions are considered: (1) an isolated OHC, (2) an OHC loaded by the stiffness K_bm of the basilar membrane, (3) the same after the addition of the mass m_bm of the basilar membrane, and (4) the same after the inclusion of the damping λ_bm of the basilar membrane. (E) The receptor potential is shown under the identical circumstances.

We can use the model to calculate the cell’s dynamic modulus (SI Appendix, section 6). The imaginary part of the modulus, which corresponds to damping, is only 1/1,000th that of other cells (31, 32). By virtue of their unusual cytoskeletal structure, OHCs have evidently evolved to minimize damping so that length changes owing directly to membrane-potential stimulation decrease significantly only for driving frequencies much higher than the characteristic frequency of the cell (33).

The operation of prestin is represented in the model by introducing into the plasma membrane a piezoelectric element with a linear response coefficient p and by increasing the stiffness K_p of the plasma membrane–prestin complex to match measurements of OHC stiffness (27). Because washout of 9AC restores somatic motility and has a negligible effect on the imaginary part of Z_ohc, prestin contributes little additional damping. The electrodynamics of an OHC is described by a simple circuit including the apical and basolateral conductances and capacitances of the cell (Fig. 2C and SI Appendix, Table S1).

To separate the effects of somatic motility from the influence of hair-bundle nonlinearity and activity, we consider the linear response of an OHC to sinusoidal changes in the bundle’s conductance (SI Appendix, section 7). A maximal increase in the conductance produces an OHC extension of over 200 nm and a low-frequency receptor potential exceeding 10 mV (Fig. 2 D and E). Near the 14-kHz characteristic frequency of the cell, however, the responses decrease to less than 50 nm and 4 mV owing to the membrane’s time constant. If the cell is loaded by the stiffness of the basilar membrane, the extension declines by more than an order of magnitude and there is a small increase in the receptor potential. Addition of the basilar membrane’s mass introduces a resonance at 14.1 kHz, increasing the extension at that frequency 30-fold. A small resonance and antiresonance appear in the receptor potential owing to the piezoelectric reciprocity associated with somatic motility, but their effect is negligible in comparison with that on the OHC’s extension. The resonant effect is quite sensitive to damping by the basilar membrane and organ of Corti: Introducing damping for the basilar membrane equal to that of a single OHC halves the resonant extension. Although the damping associated with deformation of the basilar membrane and supporting cells is unknown, it certainly exceeds this amount.

Active Outer Hair Cell.

We may now combine the descriptions of active hair-bundle motility and somatic motility to model the response of a high-frequency OHC in situ. In the actual cochlea the hair bundle is mechanically linked to the rest of the organ of Corti and basilar membrane and can accordingly apply forces to these structures (Fig. 1A). To investigate the importance of these forces in amplification we can remove them from the model by holding the hair cell’s apical surface at a fixed position and examining the response of an OHC to forcing of the hair bundle.

To apply the hair-bundle model at the 14-kHz place we must scale its parameter values appropriately. The two main changes are that a high-frequency hair bundle is shorter and has a greater conductance than a low-frequency bundle (SI Appendix, section 8). The decrease in length raises the bundle’s stiffness and reduces its damping. Because both K_a and α depend on the transduction channel’s Ca²⁺ conductance, active hair-bundle motility is also affected.

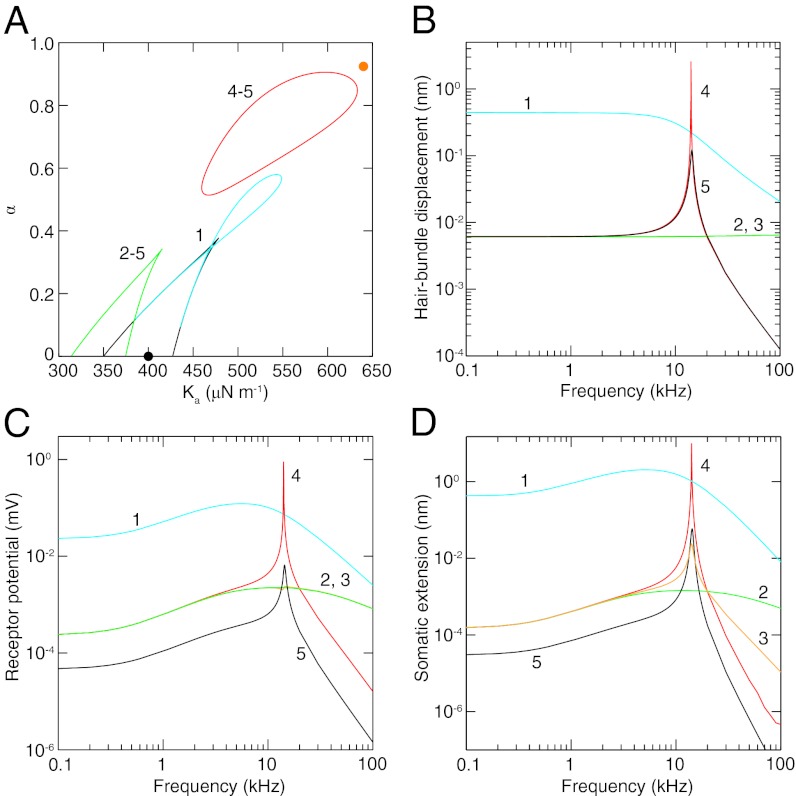
The response of an OHC depends critically on the values of K_a and α, which control active hair-bundle motility. For an unloaded OHC a loop of Hopf bifurcations adjoins a wedge of fold bifurcations in the state diagram (Fig. 3A). The hair bundle’s displacement is low-pass-filtered, however, because the operating point lies too far from the Hopf bifurcations for significant frequency tuning (Fig. 3B). In contrast, the receptor potential and thus the OHC extension exhibit broad tuning (Fig. 3 C and D). This effect results from the dependence of the receptor current on the difference between bundle displacement and adaptation-spring extension. Because these two movements decrease at different rates with increasing frequency, their difference is frequency-tuned (SI Appendix, section 9).

Fig. 3.

(A) A state diagram describes the dynamics of a 14-kHz OHC under different conditions (SI Appendix, Table S1): (1) an active, unloaded OHC, (2) an active OHC with its soma loaded by the basilar-membrane stiffness K_bm and damping λ_bm and its hair bundle loaded by the effective tectorial-membrane and basilar-membrane stiffness K_tm, (3) similar conditions with the basilar membrane’s mass m_bm added, (4) similar conditions with the tectorial membrane’s mass m_tm added, and (5) with hair-bundle activity removed by reducing K_a and α. Under conditions 2–5 the tectorial membrane’s damping coefficient λ_tm is negative to capture the effect of somatic feedback. Wedge-shaped regions of bistability are demarcated by lines of fold bifurcations. Inside the regions enclosed by the cyan loop and red line of Hopf bifurcations the system oscillates spontaneously; elsewhere the system is monostable. The orange and black circles denote the operating points for an active and a passive hair bundle, respectively. (B) Hair-bundle displacement is shown as a function of the frequency of sinusoidal hair-bundle stimulation with an amplitude of 13 pN. (C) The receptor potential of an OHC is shown as a function of the stimulus frequency. (D) The somatic extension of an OHC is shown as a function of the stimulus frequency. In each instance operation of the system near the line of Hopf bifurcations greatly enhances the response.

When the hair bundle is loaded by the tectorial membrane’s stiffness, and even though the damping is reduced to account for electromotile feedback to the bundle (19), the state diagram loses the loop of Hopf bifurcations and displays a shift in its bistable region (Fig. 3A). Loading the cell’s soma with the stiffness and damping of the basilar membrane has no effect on the state diagram by construction, but it would influence hair-bundle dynamics in a fully coupled system. The net effect of raising the load is to reduce all of the response magnitudes considerably over the frequency range considered (Fig. 3). The addition of the basilar membrane’s mass has no effect on the state diagram or the hair-bundle displacement and changes the receptor potential little. In comparison, the OHC’s extension exhibits a passive resonance that increases the response at 14.1 kHz by a factor of 17.

When the mass of the tectorial membrane is introduced, a line of Hopf bifurcations appears in the state diagram near the hair bundle’s operating point. This proximity greatly enhances all of the OHC’s responses near the resonant frequency of the system. The amplitude of the bundle’s oscillation at 14.1 kHz increases by a factor of over 400, amplifying the receptor potential and thus the somatic extension by the same amount.

The activity of the hair bundle enhances somatic extension at 14.1 kHz by more than 100-fold as a result of two independent effects. First, hair-bundle activity allows the system to operate near a Hopf bifurcation at which active amplification can occur. Second, the activity of the hair bundle situates the system’s operating point where the transduction channels are most responsive to bundle displacement. The open probability is much more sensitive to displacement when the reference probability lies near one-half in the active case than when it approaches unity in the passive case (SI Appendix, Fig. S1A). Hair-bundle activity raises the receptor potential at all frequencies by a factor of 5 simply because the transduction channels are more sensitive to bundle displacement. The cochlear response therefore depends on the slope transduction conductance (20), but active amplification by the hair bundle does not require that this conductance be maximized. Conversely, it is in principle possible to maximize the slope conductance without the hair bundle’s being active.

Discussion

To address the basis of high-frequency amplification in the cochlea we have constructed a physiologically detailed description of an active OHC. The representation of fast adaptation, a Ca²⁺-dependent adaptation spring that responds at high frequencies, reproduces experimental observations of hair-bundle motion and transduction currents. The model of somatic mechanics captures measurements of the soma’s impedance. Our analysis reveals that the damping of the OHC’s soma is remarkably small, of the same magnitude as the damping of an unloaded hair bundle.

Mass loading of an active hair bundle can lead to a sharply tuned receptor potential, for the load’s inertia reduces the reactive load on the bundle such that its active motility can influence the cochlear partition (6, 12). The motility of a hair bundle is limited at high frequencies by damping (34) that must be counteracted by positive feedback from the soma (19). The presence of this feedback mechanism is supported by observations showing that somatic motility can cause bundle motion by applying forces on the OHC’s apical surface (35, 36).

The present results clarify the mechanism for amplification described in a cochlear model coupling active hair-bundle motility and somatic motility (19). The large OHC extensions observed in that model result from the mechanism described here, amplification of the receptor potential by active hair-bundle motility and positive somatic feedback. The mechanism is the same even though the earlier model employs a different representation of adaptation, for many formulations produce similar bundle dynamics (12). In both models, enhanced sensitivity and sharp frequency selectivity require a Hopf bifurcation resulting from the combination of active hair-bundle motility and positive feedback from somatic motility.

In the actual cochlea a wave travels along the cochlear partition owing fluid coupling between cochlear segments (2, 4, 37). The measured response results from a combination of wave propagation and the response to local forcing. When the model operates close to a Hopf bifurcation the simulated tuning and sensitivity, defined by the ratio of response to input, can exceed those observed experimentally (5) for two reasons. First, we have not included in the model noise that would diminish both sensitivity and frequency selectivity (2, 9). Second, the model represents a single cochlear segment and therefore omits the viscosity of the fluid surrounding the cochlear partition and associated with wave propagation.

Despite its simplicity, the model of an active OHC offers several testable predictions. The most important is that, when the OHC is situated in the cochlea, somatic length changes are tuned owing to a combination of active hair-bundle motility and cochlear inertia. Forcing the tectorial membrane directly should therefore result in a tuned basilar-membrane response that diminishes when either active hair-bundle motility or somatic motility is blocked. In accordance with a role for cochlear inertia in tuning the length changes of OHCs, exciting somatic motility by injection of current into the cochlea elicits a tuned response of the basilar membrane (38). This result does not distinguish, however, among the three inertial effects on OHC extension: piezoelectric reciprocity bearing on the receptor potential, somatic loading altering OHC extension, or hair-bundle loading affecting the transduction current.

Another significant prediction is that loading the hair bundle of an active OHC with a mass similar to that of the tectorial membrane could cause spontaneous bundle oscillations that would alter the membrane potential and thereby trigger spontaneous somatic vibrations. These vibrations could in turn power the spontaneous otoacoustic emissions that emerge from healthy ears (39).

The model also predicts that reducing the tectorial membrane’s stiffness or damping or increasing its mass should result in more sensitive and more sharply tuned responses to low-amplitude acoustic stimulation. A reduction in damping would explain the improvement in tuning at high frequencies seen in a mutant mouse with a modified tectorial membrane (40). In contrast, there is no change in the responses of a mutant mouse with reduced tectorial-membrane stiffness at frequencies greater than those studied here (41), indicating that this stiffness may not be large at high-frequency locations. In this case the role of the membrane’s mass may be to counteract the passive stiffness of the hair bundle itself.

Another mutant mouse in which the tectorial membrane is detached from the hair bundles displays substantially reduced sensitivity and tuning in response to acoustic stimulation but not to electrical stimulation (42). This is consistent with the model, for the bundles are not stimulated significantly by acoustic input in the mutant and thus active hair-bundle motility cannot amplify the OHC’s receptor potential. However, electrical stimulation seems to dominate the OHC’s membrane potential such that active hair-bundle motility has little effect in either mutant or wild-type mice.

It has been suggested that the main effect of hair-bundle activity is to adjust the operating point of the transduction channels, thus maximizing the sensitivity of the transduction current to bundle displacement (20, 43). Adaptation does set the channels’ operating point, but so do other passive properties of the system. The chief purpose of active hair-bundle motility is instead to tune and amplify bundle motion in concert with that of the rest of the cochlear partition, thus tuning and increasing the receptor potential that drives somatic motility. Because hair-bundle activity increases with the characteristic frequency (SI Appendix, section 8) and bundle motility amplifies somatic motility, the importance of somatic motility also grows with the characteristic frequency.

Although several studies have addressed how OHCs might function at high frequencies in the cochlea, there is no consensus owing to the lack of experimental verification. It has been proposed that the RC time constant is overcome by driving somatic motility with the unattenuated extracellular potential (44), negative feedback to increase the cutoff frequency of the receptor potential (45), activation of basolateral ion channels (14), tuning and high-pass filtering of the receptor potential through resonant electromechanical filtering of the input to a passive hair bundle (43), tuning of OHC extension by inertial loading of the soma despite low-pass filtering of the receptor potential (46), a reciprocal effect of somatic motility on the receptor potential (47, 48), or resonant tectorial-membrane filtering of the input to a passive hair bundle that leads to a tuned receptor potential (10, 37, 49). Although the last three mechanisms make contributions in the present model, and the other processes may also have effects, the mechanism described here is simple and requires few assumptions.

The force produced by an OHC is maximized when the cell is prevented from changing length by its load (14, 43, 50). OHCs must change length, however, to amplify the motion of the cochlear partition in vivo. Although the impedance of the structures surrounding the OHCs might be matched with that of the OHCs’ somata to maximize power transfer (46, 51), this condition would maximize neither efficiency nor vibration amplitudes (46). Here we focus on how an active OHC can produce displacements similar to those seen experimentally despite the large cochlear load.

There has been a similar emphasis on force production by the active hair bundle (11, 20, 21, 35). In the model we have deliberately prevented the hair bundle from applying forces on the basilar membrane by holding the apical surface of the cell in a fixed position (SI Appendix, section 9). The results show that active hair-bundle motility need amplify only the motion of the bundle itself, thus enhancing the receptor potential, to boost the motion of the cochlear partition as a whole. The transduction channel’s gating force must be sufficiently large, however, for hair-bundle activity to amplify the motion of a loaded bundle. For a 4-kHz bundle, the force required is much smaller (10 pN) when the tectorial membrane’s mass is taken into account than when that mass is neglected (80 pN) (19) (SI Appendix, section 3). This observation emphasizes the importance of the bundle’s inertial load. Effective hair-bundle motility at 14 kHz necessitates almost twice the force (19 pN) required for a 4-kHz bundle. The magnitudes of the gating forces used here resemble those used in another cochlear model (20) but exceed many other determinations owing to underestimation of the channel’s sensitivity to bundle displacement (SI Appendix, section 3).

Active hair-bundle motility is ubiquitous among tetrapod vertebrates (52) and likely occurs in more basal clades as well. The present model suggests an evolutionary progression in which high-frequency hearing arose when a preexisting auditory amplifier implemented by active hair-bundle motility was augmented with an additional source of mechanical energy stemming from somatic motility.

Materials and Methods

Analytical calculations and experimental data fitting were performed with the assistance of Mathematica 7. Numerical integration was accomplished with MATLAB 7. Additional details are provided in the SI Appendix.