Fig. 1.
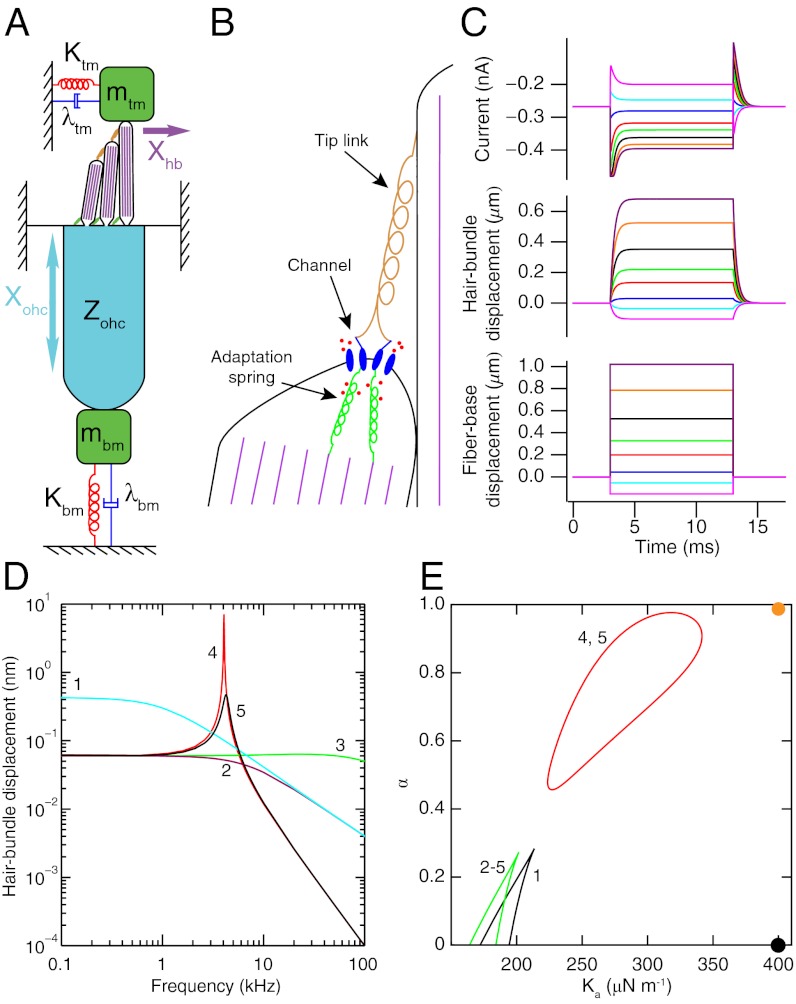
(A) A schematic drawing portrays an OHC and the associated cochlear structures that provide its mechanical loads. The hair bundle has three rows of stereocilia with progressively increasing heights. Filled with filamentous actin (purple), each stereocilium pivots about its base and is connected to its tallest neighbor through a tip link (orange). The bundle is loaded by the mass mtm, damping λtm, and stiffness Ktm associated with the tectorial membrane. The soma of the OHC confronts the mass mbm, damping λbm, and stiffness Kbm of the basilar membrane. The mechanical impedance Zohc of the soma is described in Fig. 2A. The hair bundle’s displacement Xhb and the soma’s extension Xohc are indicated by arrows. (B) Adjacent stereocilia within a hair bundle are connected by a tip link at the lower end of which are thought to reside two mechanically gated cation channels. Ca2+ (red circles) enters the stereocilium through the channels and binds to the adaptation springs connecting the channels to the actin cytoskeleton (purple), thereby reducing their stiffness. The deformation of the membrane at the tip of the shorter stereocilium by the tension in the tip link is known as tenting. (C) Step displacements of the base of a flexible fiber attached atop the hair bundle of an active 4-kHz hair cell evoke a simulated hair-bundle displacement and transduction current. (D) The hair bundle’s simulated response to sinusoidal stimulation 13 pN in amplitude is shown under different conditions (SI Appendix, Table S1). (1) The active hair bundle is loaded by a fiber’s stiffness Kf and damping λf. (2) The stiffness of the load is increased to equal the effective stiffnesses of the tectorial membrane and basilar membrane Ktm. (3) The load’s damping λtm is given a negative value to capture the effect of somatic feedback. (4) The mass mtm of the tectorial membrane is added. (5) Hair-bundle activity is removed by reducing the Ca2+ sensitivity α. (E) A state diagram, parameterized by α and the adaptation springs’ maximal stiffness Ka, describes the bundle dynamics associated with the various conditions enumerated above. Wedge-shaped regions of bistability are demarcated by lines of fold bifurcations. Inside the region enclosed by a red line of Hopf bifurcations the hair bundle oscillates spontaneously; elsewhere the bundle is monostable. The orange and black circles denote the operating points for an active and a passive hair bundle, respectively.