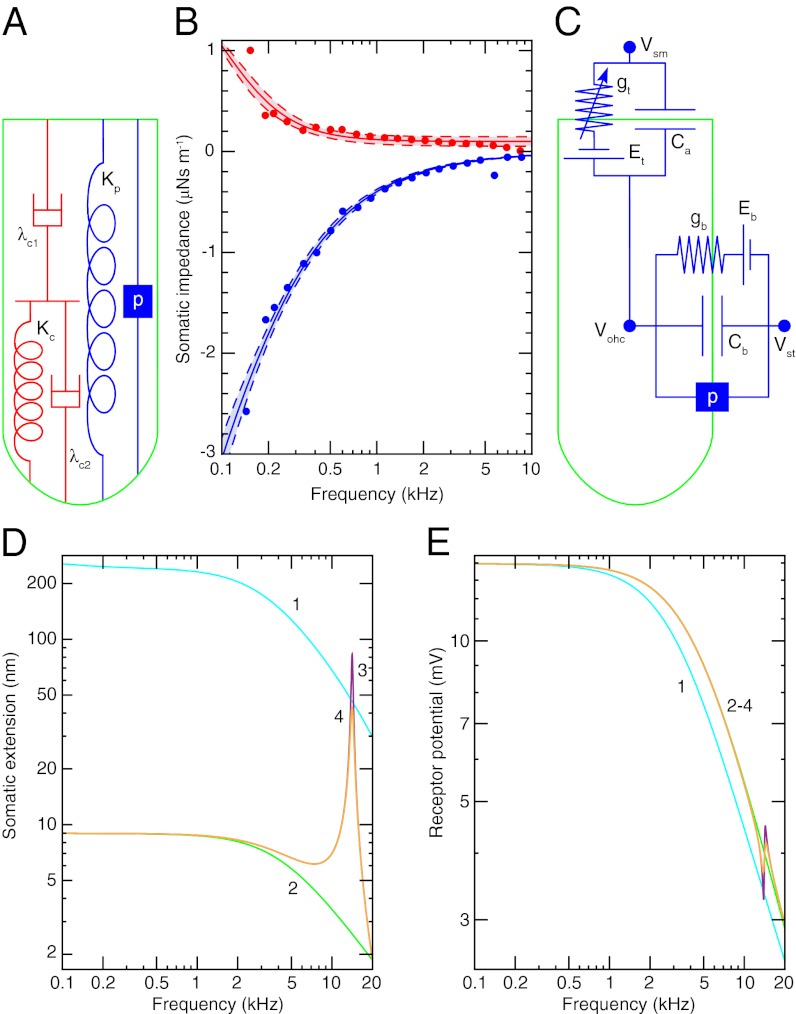
Fig. 2.

(A) The cortical lattice and subsurface cisternae of an OHC are described by the two dashpots λ_c1 and λ_c2 and the spring K_c. The plasma membrane is represented by a spring K_p in parallel with a piezoelectric element p betokening the prestin molecules. (B) The experimentally determined real part (red circles) and imaginary part (blue circles) of the mechanical impedance of a 14-kHz OHC are simultaneously fit by the model depicted in A with the constraints of no electromotility, 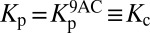, and p = 0 (R² > 0.98, solid lines). The fit yields K_c = 1.32 ± 0.04 mN⋅m⁻¹ (P value < 10⁻²⁸), λ_c1 = 2.00 ± 0.28 μN⋅s⋅m⁻¹ (P value < 10⁻⁷), and λ_c2 = 104 ± 25 nN⋅s⋅m⁻¹ (P value < 0.001). The dashed lines represent 95% confidence intervals. (C) The transduction current flowing across the apical membrane of the OHC responds to changes in the potential difference between the hair cell’s interior and the scala media, V_ohc − V_sm. The potentials of the scala media V_sm at the OHC’s apical surface and of the scala tympani V_st at the OHC’s basolateral membrane are approximately constant. The apical membrane acts as a capacitor C_a in parallel with a variable conductance g_t that represents the transduction channels and has a reversal potential E_t. Driven by the reversal potential of the basolateral somatic membrane E_b, current exits the OHC through its basolateral membrane, which is described by a conductance g_b in parallel with a capacitor C_b and a piezoelectric element p. (D) The model predicts the change in somatic length of a 14-kHz OHC in response to sinusoidal changes in hair-bundle conductance of maximal amplitude around the reference value (SI Appendix, Table S1). Four conditions are considered: (1) an isolated OHC, (2) an OHC loaded by the stiffness K_bm of the basilar membrane, (3) the same after the addition of the mass m_bm of the basilar membrane, and (4) the same after the inclusion of the damping λ_bm of the basilar membrane. (E) The receptor potential is shown under the identical circumstances.