Abstract
Understanding anatomical connectivity is crucial for improving outcomes of deep brain stimulation surgery. Tractography is a promising method for noninvasively investigating anatomical connectivity, but connections between subcortical regions have not been closely examined by this method. As many connections to subcortical regions converge at the internal capsule (IC), we investigate the connectivity through the IC to three subcortical nuclei (caudate, lentiform nucleus, and thalamus) in six macaques. We show that a statistical correction for a known distance-related artifact in tractography results in large changes in connectivity patterns. Our results suggest that care should be taken in using tractography to assess anatomical connectivity between subcortical structures.
Key words: connectivity, deep brain stimulation, diffusion tensor imaging, internal capsule, MRI, neurostimulation, subcortical structures, tractography
Introduction
Deep brain stimulation (DBS) is a successful treatment for refractory Parkinson's disease and other movement disorders (Deuschl et al., 2006; Machado et al., 2006; Rodriguez-Oroz et al., 2005). The primary targets of DBS are subcortical gray matter structures (Johnson et al., 2008). Mapping con-nections among these structures may prove important for improving treatment outcomes while providing insight into deep brain circuits such as the cortico-striato-pallido-thalamic motor circuit (McIntyre et al., 2004; McIntyre and Hahn, 2010).
Tractography can noninvasively map anatomical connections (Behrens et al., 2003; Hagmann et al., 2008a; Skudlarski et al., 2008). However, tractography is an indirect measure of anatomical connectivity. Great caution must be taken before interpreting tracks generated via tractography as representing actual white matter fascicles (Yamada, 2009). Due to the propagation of uncertainty in the fiber orientation probability density functions, there is a known artifact in probabilistic tractography in which proximal regions are systematically more highly connected than distal regions (Jones, 2008; Morris et al., 2008). Even along well-organized, straight fiber tracts, voxels close to a seedpoint will have a higher percentage of tracks than voxels further from the seedpoint because of the propagation of uncertainty (Jones, 2008). The result is a flare pattern of high track frequency in regions near the seedpoint where uncertainty is low and low track frequency further from the seed as uncertainty grows (Morris et al., 2008). Subcortical structures are particularly susceptible to this bias because of their proximity to each other. Correcting this bias may prove essential in establishing probabilistic tractography as a noninvasive tool for measuring anatomical connectivity. However, almost no work has been done to correct for uncertainty propagation in probabilistic tractography. Recently, Morris and associates (2008) have introduced a statistical correction (the Morris correction) to address this issue, but it has not been widely used.
The internal capsule (IC), a bundle of white matter fibers, is particularly important in DBS. The IC is highly connected to both subcortical and cortical structures and thus has the potential to spread stimuli far from the site of activation (Haber and Brucker, 2009). Such stimulus spread could be beneficial, allowing stimulation of a variety of target structures from one activation site. However, unintentional stimulation of the wrong structures could lead to side effects (Xu et al., 2010). Of practical importance is that white matter requires lower stimulation thresholds than gray matter nuclei—a beneficial feature for DBS performance in general (Frankemolle et al., 2010).
In this work we segment the IC in 6 macaques based on anatomical connectivity to three subcortical nuclei: the caudate, lentiform nucleus (LN), and thalamus. We perform segmentation with and without the Morris correction. The principal foci of this work are
Using tractography we demonstrate connection among deep brain structures correcting for the known distance bias. This is one of the few tractography studies of subcortical connections.
We find that the Morris correction has a large impact on connectivity results. Without the correction, the patterns of connectivity are largely governed by proximity. With the correction we find many examples in which proximity does not determine connectivity. In some studies the correction reveals areas of the IC with no significant connections to one or more target structures.
We find that the caudate is most strongly and consistently connected to the anterior limb of the IC. The LN is most strongly and consistently connected to the lateral genu of the IC. The thalamus is most strongly and consistently connected to the medial genu of the IC.
Methods
Imaging and postprocessing
Six rhesus macaques (macaca mulatta) were scanned under a protocol approved by the Cleveland Clinic Institutional Animal Care and Use Committee. Animals were anesthetized with a propofol drip and held snugly on a Plexiglas board to minimize motion. High angular resolution diffusion imaging (HARDI) (Tuch et al., 2002) (71 diffusion weighted image volumes with b=1000 sec/mm2, 8 b=0 images) was performed at high spatial resolution (96×96 mm FOV, 64×64 matrix, 1.5 mm slice thickness, yielding 1.5×1.5×1.5 mm voxels) with TR=2000 ms, TE=87 ms, NEX ranging from 23 to 36 (corresponding to acquisition time of 4–6 h) on a Siemens 3 tesla Trio (Erlangen, Germany). Partial brain scans (fourteen or fifteen 1.5-mm-thick slices) centered on the deep brain structures were performed to improve signal-to-noise ratio (SNR). The SNR was approximately 40 and 10 for the b=0 and diffusion-weighted images, respectively. At each voxel, the diffusion tensor was calculated using a standard log-linear fit (Basser et al., 1994), and fractional anisotropy (FA) was calculated from the diffusion tensor (Basser and Pierpaoli, 1996). The fiber orientation distribution (FOD) was calculated at each voxel using regularized spherical deconvolution (Sakaie and Lowe, 2007; Tournier et al., 2004). The FOD was then used as the basis of probabilistic tractography.
Tractography
We assessed anatomical connectivity between the IC and three surrounding subcortical structures: caudate, LN, and thalamus. For each study, caudate, LN, and thalamus region of interests (ROIs) were drawn by hand on coronal and axial FA images on the right side of the brain using the Saleem and Logothetis MRI histology atlas of the rhesus macaque as a reference (Saleem and Logothetis, 2006). We limited the IC at the posterior using a line between the posterior borders of thalamus and LN and at the anterior using a line between anterior borders of caudate and LN (Zarei et al., 2007). The medial and lateral borders of the IC were easy to distinguish because of the sharp contrast between the bright white matter of the IC and the dark surrounding gray matter. The superior and inferior borders were defined based on the boundaries of the caudate, LN, and thalamus in conjunction with the Saleem atlas. Figure 1 shows an example of a manual ROI for one study.
FIG. 1.
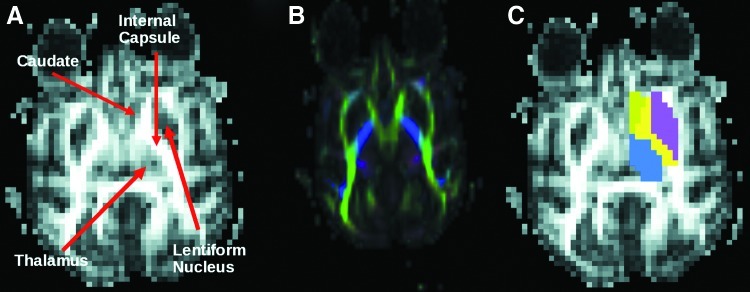
Example of manual ROIs drawn on an FA map. (A) The FA map with labeled arrows pointing to the IC, caudate, LN, and thalamus. (B) The color FA image, and (C) the ROIs drawn on this slice. ROI, region of interest; FA, fractional anisotropy; IC, internal capsule; LN, lentiform nucleus.
Probabilistic tractography was used to define anatomical connectivity between each voxel in the IC and the three subcortical structures of interest. We ran an in-house algorithm using a rejection sampling approach based on the FOD (Lowe et al., 2008; Tournier et al., 2005). We generated 250 tracks per IC seed voxel with a step length of 1.125 mm and maximum bending angle of 90°. Tracks initiated in the seed region (IC) proceeded throughout the entire brain until the tracks left a mask defined using a robust range threshold on the b=0 image (Smith, 2002).
The Morris correction
As the tractography algorithm is probabilistic, a given voxel in the IC typically exhibited connections to each nucleus. To correct for distance-related bias, we performed the correction developed by Morris and associates (2008). The correction provides a framework for determining whether connectivity between a seed voxel and a given target is statistically significant. The method has been shown to account for distance artifact in anatomical connectivity results. The key insight of the Morris correction is to compare track counts generated by probabilistic tractography to a null distribution, thus allowing the statistical comparison. In practice, the null distribution is simply achieved by repeating the tractography with an isotropic FOD. The null distribution therefore provides a map of connections due purely to chance instead of the directionality inferred from diffusion anisotropy.
Connection profiles and segmentation
To assess the impact of the Morris correction, we generated an anatomical connectivity profile of the IC to each subcortical nucleus and then performed a so-called hard segmentation of the IC (Zarei et al., 2007). The anatomical connectivity profiles were generated by superimposing the target ROIs on the whole brain tractography results seeded from each IC voxel and adding up the number of tracks that intersect that ROI. The hard segmentation classified each IC voxel according to which target had the highest number of connecting tracks. The connectivity profiles and the segmentation were performed with and without the Morris correction.
Results
Figure 2 demonstrates the overall impact of the Morris correction. Connectivity through the IC from caudate is shown with and without the Morris correction. For comparison, the null distribution map is also shown. As the null distribution map does not include information from tissue microstructure, it primarily reflects the proximity between individual voxels of the IC and the caudate. The null distribution map and the connectivity map without the Morris correction demonstrate a high degree of similarity. After the correction, the connectivity profile is qualitatively different from the null distribution map.
FIG. 2.
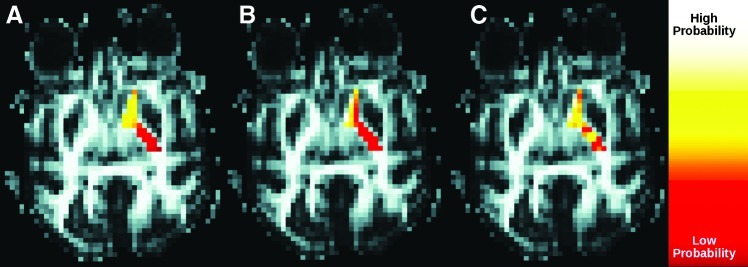
Overall impact of Morris correction on profile of connections from caudate through the IC. (A) shows the null distribution map. (B) and (C) show connection profiles before and after the correction, respectively.
Figure 3 demonstrates the effect of the Morris correction on the anatomical connectivity profile. Before the correction, regions of IC close to the caudate are more connected than those further away—there are many connections from caudate running through the anterior limb of the IC, fewer connections between caudate and genu of IC, and fewer still from caudate running through the posterior limb of IC. The correction results in a large reorganization of the connection pattern. The anterior limb is still highly connected. However, a portion of the genu and posterior limb (both relatively far from the caudate) become highly connected after the correction. Some of the posterior limb remains weakly connected, showing that the impact of the filter is not uniform. Variability of connectivity is particularly high in the posterior limb of IC even after the correction.
FIG. 3.
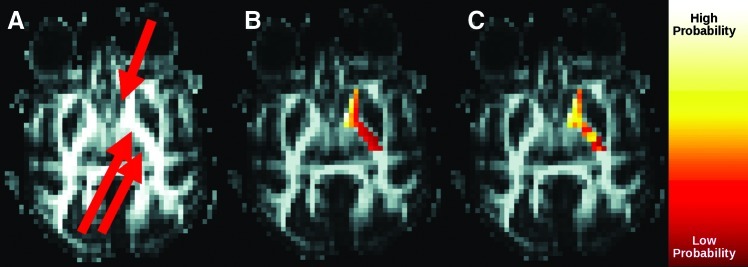
Effect of Morris correction on connectivity between IC and caudate. (A) Fractional anisotropy image indicating location of the caudate (single arrow) and IC (double arrow). Connectivity (B) without and (C) with correction.
Figures 4 and 5 show reorganization of IC connections to the LN and thalamus due to the Morris correction. Without the correction, regions located closer to the LN or thalamus are systematically more connected than those further away. After the correction, lateral genu of IC shows high connectivity to the LN, whereas medial genu of the IC shows high connectivity to thalamus. These patterns are consistent among subjects.
FIG. 4.
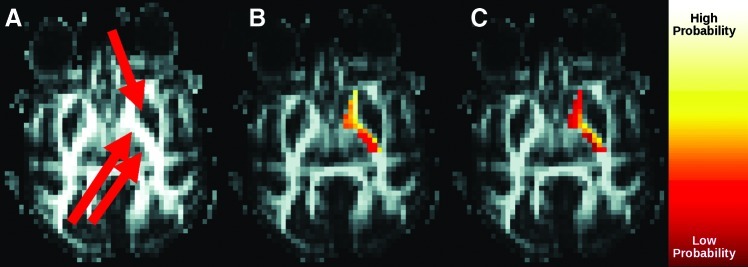
Effect of Morris correction on connectivity between the IC and LN. (A) Fractional anisotropy image, indicating location of the LN (single arrow) and IC (double arrow). Connectivity (B) without and (C) with correction.
FIG. 5.
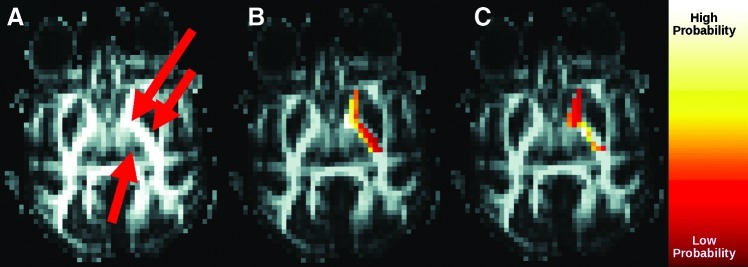
Effect of Morris correction on connectivity between the IC and thalamus. (A) Fractional anisotropy image indicating location of the thalamus (single arrow) and IC (double arrow). Connectivity (B) without and (C) with correction.
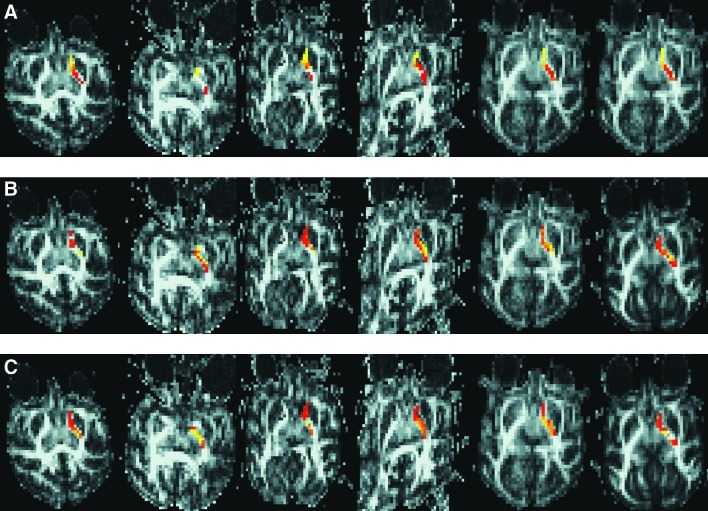
Figure 6 shows the connectivity profile after correction for each of the three targets across the six studies. Row A shows the connectivity profiles for the caudate, row B for the LN, and row C for the thalamus. We observe similar connection patterns to those mentioned above where caudate is most connected to anterior limb of IC, LN to lateral genu, and thalamus to medial genu. Significantly, with the correction we see that numerous regions across the different targets have no significant connections at all. Many voxels in the genu of the IC have no significant connections to the caudate (row A). Interestingly, there are still significant connections between the caudate and the distant posterior IC even in studies where voxels in the genu of the IC show no significant connection. The LN shows least connection and occasional dropout of connection to posterior limb of IC and medial genu. The thalamus has highest connectivity throughout the entire IC with minimal number of insignificantly connected voxels in the anterior limb and lateral genu.
FIG. 6.
Connectivity maps after the Morris correction for all three structures across all six studies. The top row (A) shows connectivity profiles between IC and caudate, the middle row (B) profiles between IC and LN, and the bottom row (C) between IC and thalamus. Across the three structures we observe regions in the IC with no significant connections.
Hard segmentation provides a means for comparing connection differences among the three target structures. The statistical correction had a strong impact on hard segmentation results as 23%±6% of voxels change classification. However, there does not appear to be an obvious pattern to which regions change classification because of the correction. Figure 7 shows hard segmentation results for all six studies before (row A) and after (row B) the correction.
FIG. 7.
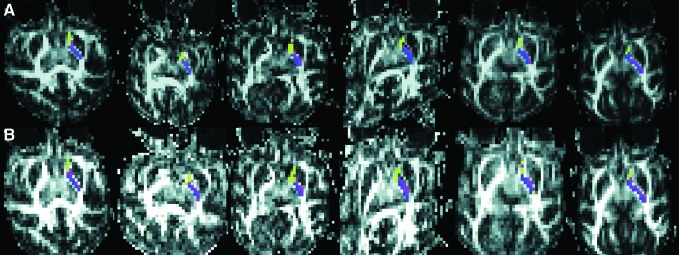
Impact of correction on hard segmentation across the six studies. Of the three target structures green regions had the highest probability of connection to caudate, and purple and blue to LN and thalamus, respectively. The top row (A) shows segmentation before the correction, and the bottom row (B) after correction. Many voxels in the IC change classification because of the correction, and although patterns seem similar in the top and bottom row, it is not clear how the Morris correction impacted results.
Discussion and Conclusions
We investigated anatomical connectivity of the IC to three bordering subcortical structures (caudate, LN, and thalamus) with particular focus on the impact of a statistical correction to account for distance-related bias. In general, the correction shifts connectivity patterns away from one in which proximity determines the degree of connectivity. After the correction, the caudate is most strongly and consistently connected to the anterior limb of the IC with some connection to the posterior limb. The LN is most strongly and consistently connected to the lateral genu of the IC. The thalamus is most strongly and consistently connected to the medial genu of the IC.
Tracer studies provide support for the results. Leichnetz and Astruc (1976) found connections between the anterior limb of the IC and the caudate. Yeterian and Pandya (1991) noted a similar result. Morecraft and associates (2002) observed a medial–lateral division in the anterior IC where medial regions were more connected to caudate and lateral regions to LN. These results agree with the caudate and LN connectivity maps and the hard segmentation results. Tanaka (1976) found some evidence that medial regions in the genu and posterior limb were connected to the thalamus. However, these tracer studies primarily focused on cortical–subcortical connections and only noted if tracts passed through the IC along the way from subcortical nuclei to the cortex. Existing tracer studies therefore do not provide a comprehensive picture of connectivity between subcortical nuclei and the IC.
This study complements recent tractography-based studies of connectivity of the IC. Zarei and associates (2007) studied connectivity of cortical structures through the IC, showing connectivity largely consistent with anatomical tracer studies. Sullivan and associates (2010) showed age-related changes of FA and diffusivity measures in IC segmented by cortical connections. In general, patterns of cortical connectivity of the IC show organization along the anterior–posterior direction. However, we find a distinct pattern in the organization of connections to subcortical nuclei along the lateral–medial direction.
The individual connectivity profiles may be more useful for DBS presurgical planning than hard segmentation results. To illustrate, Figure 8 compares corrected hard segmentation with connectivity profiles indicating connectivity between IC and each of the three subcortical nuclei of interest. Although hard segmentation classifies the indicated voxel as most highly connected to thalamus, connectivity to caudate is nearly as large. This region would therefore be a poor target if selective stimulation of a single nucleus is expected to provide optimum therapeutic benefit.
FIG. 8.
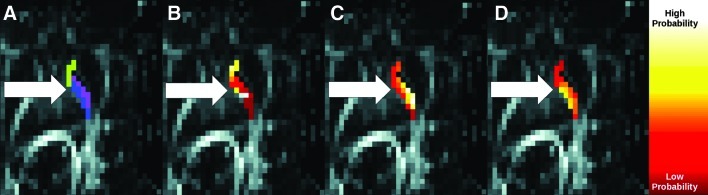
Comparison of hard segmentation (A) with connectivity profiles for caudate (B), LN (C), and thalamus (D). The arrow indicates a region most connected to thalamus, but which is also highly connected to caudate.
This study was limited with regard to the ROIs. These limitations will be addressed in future studies. Although we followed the methodology of Zarei and associates (2007) using FA maps to define ROIs, ROI selection is typically performed on high-resolution anatomical images. However, HARDI images in this study covered only part of the brain in the inferior–superior direction as part of a trade-off between the need for high spatial resolution, adequate SNR, and memory limitations of the scanner. Unfortunately, we found it impossible to reliably coregister these partial-brain images with high-resolution anatomical scans with standard techniques. Further, distortions from the echo planar acquisition for the HARDI images typically result in the need for manual editing of ROIs using the FA maps after coregistration.
The inability to coregister to anatomical scans also prevented us from coregistering studies into a common space. Consequently, we were unable to generate average connectivity maps or quantify map consistency.
ROIs were determined manually, leading to systematic errors that can be addressed by automatic segmentation. Although there are widely used tools for automated segmentation of cortical structures, fewer tools exist for segmenting subcortical structures. Further, these tools were optimized for human, not macaque, anatomy. As macaques are an important model for studies of the central nervous system, dedicated, automated methods for anatomical analysis of macaque images are an important need for the research community in general.
Although we follow others' precedents in using FA to identify regions (Zarei et al., 2007), other diffusion-based contrasts can be used to identify regions. For example, generalized FA (Tuch, 2004) should improve contrast particularly in regions with crossing fibers and partial volume averaging.
A number of algorithms exist for tractography. Streamline tractography (Mori et al., 1999) is commonly used, but probabilistic tractography is required to perform the Morris correction. Although we have demonstrated the use of the Morris correction using an in-house algorithm, the correction is completely compatible with publicly available tools such as FSL (Smith et al., 2004), Camino (Cook et al., 2006), and MRtrix (J-D Tournier, Brain Research Institute, Melbourne, Australia; www.brain.org.au/software/ [last accessed April 15, 2011]). Future work will evaluate the impact of the correction on different probabilistic tractography methodologies.
The definition of anatomical connectivity is an open question for the research community at large. One important methodological issue is partial volume averaging. As the subcortical regions are small, a relatively large layer of voxels at the border of each region is, in fact, a mixture of the tissue of interest and other tissue. A substantial fraction of tracks passing through these border voxels therefore do not truly intersect the tissue of interest, but neighboring tissue. The approach taken here simply assumes that if a track intersects the user-defined ROI, it intersects the tissue of interest. The partial volume effect may be addressed by close examination of the trajectory of each track, excluding those that graze the edge of the tissue of interest. Future work will examine the extent of this effect on measured connectivity values.
The rejection sampling algorithm used to generate the tracks is simple, and further refinements may improve performance. Partial volume effects due to crossing fibers are accounted for by use of the FOD. However, beyond the relatively permissive 90° bending criterion, no further constraints were placed on track shapes. For example, tracks were not forbidden from looping back on themselves or re-entering the subcortical nuclei. Future work will examine appropriate constraints on track geometries for the assessment of anatomical connectivity.
An important distinction should be made regarding the nature of the Morris correction. The correction works on overall statistics of track counts, but not on the track geometries themselves. For example, the correction does not filter tracks with improbable shapes from a mixture of tracks with plausible and implausible trajectories. An alternative approach examining the statistics of shapes may be a valuable approach with better properties, but is beyond the scope of this article.
Relatively little work has examined anatomical connectivity of subcortical structures by noninvasive means. The work of Iturria-Medina and associates (2007, 2008) examined the connectivity patterns of a large number of brain regions, including subcortical regions. An important issue to be examined is the degree to which the Morris correction would alter such patterns.
Future work will examine the efficacy of the Morris correction and subcortical connections in detail. For example, simulations on digital phantoms can be used to quantitatively test the ability of the Morris correction to account for the distance-related falloff in anatomical connectivity. Such simulations can also be used to clarify distinctions in performance of the Morris correction in conjunction with different probabilistic tractography algorithms. Further, consistency with ground-truth studies of connectivity using anatomical tracers (e.g., Stephan et al., 2001; Modha and Singh, 2010) is another indirect method for validating anatomical connectivity results. This type of approach has been taken by Hagmann and associates (2008b).
A number of opportunities for optimizing the methodology of measuring anatomical connectivity are available. Beyond the algorithmic approaches mentioned earlier in the discussion, details of the image acquisition such as spatial resolution, diffusion-weighting, and gradient acquisition scheme can each play an important role.
Optimization requires a reliable methodology for ground-truth validation. Beside simulations and comparison with known anatomical connectivity patterns in macaques, it may also be possible to use electrophysiology measurements taken in humans during DBS placement. There have been several recent clinical studies using tractography in surgical planning for DBS. Gutman and associates (2009) analyzed the connectivity patterns of subcallosal cingulate and anterior limb of IC, two common stimulation sites for depression. Barkhoudarian and associates (2010) looked at tractography results for three DBS patients, suggesting that tractography could help clinicians characterize potential effects and side effects on a patient by patient basis. Coenen and associates (2011) used tractography to implicate the dentate-rubro-thalamic tract in controlling tremor in a single DBS patient. None of these seem to have addressed the distance artifact.
DBS is attractive to study with tractography precisely because it provides some possibility of optimizing tractography parameters via cross-validation with interoperative electrophysiology and surgical outcomes. Modeling of stimulation patterns from implanted electrodes (Miocinovic et al., 2009) can be used to determine consistency between connectivity profiles and observed clinical outcomes and side effects. Upon validation of the connectivity profiles, we hope to prospectively inform DBS implantation and stimulation parameters for improved clinical outcomes.
Acknowledgments
We gratefully acknowledge funding from NIH R01 NS047388, 5R21N9059571, R21NS059571, and the Choose Ohio First Scholarship Program.
Author Disclosure Statement
No competing financial interests.
References
- Barkhoudarian G, et al. A role of diffusion tensor imaging in movement disorder surgery. Acta Neurochir. 2010;152:2089–2095. doi: 10.1007/s00701-010-0742-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ. Mattiello J. Lebihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser PJ. Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, et al. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat Neurosci. 2003;6:750–757. doi: 10.1038/nn1075. [DOI] [PubMed] [Google Scholar]
- Coenen VA. Mädler B. Schiffbauer H. Urbach H. Allert N. Individual fiber anatomy of the subthalamic region revealed with DTI—a concept to identify the DBS target for tremor suppression. Neurosurgery. 2011;68:1069–1076. doi: 10.1227/NEU.0b013e31820a1a20. [DOI] [PubMed] [Google Scholar]
- Cook PA, et al. Camino: Open-Source Diffusion-MRI Reconstruction and Processing. In Proceedings of the 14th Meeting of ISMRM, Seattle; Washington, USA. 2006. p. 2759. [Google Scholar]
- Deuschl G, et al. A randomized trial of deep-brain stimulation for Parkinson's disease. N Engl J Med. 2006;355:896–908. doi: 10.1056/NEJMoa060281. [DOI] [PubMed] [Google Scholar]
- Frankemolle AMM, et al. Reversing cognitive–motor impairments in Parkinson's disease patients using a computational modelling approach to deep brain stimulation programming. Brain. 2010;133:746–761. doi: 10.1093/brain/awp315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutman DA. Holtzheimer PE. Behrens TE. Johansen-Berg H. Mayberg HS. A tractography analysis of two deep brain stimulation white matter targets for depression. Biol Psychiatry. 2009;65:276–282. doi: 10.1016/j.biopsych.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN. Brucker JL. Cognitive and limbic circuits that are affected by deep brain stimulation. Front Biosci. 2009;14:1823–1834. doi: 10.2741/3344. [DOI] [PubMed] [Google Scholar]
- Hagmann P, et al. Mapping the structural core of the human cerebral cortex. PLoS Biol. 2008a;6:e159. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P. Gigandet X. Meull R. Kötter R. Sporns O. Wedeen V. Quantitative Validation of MR Tractography Using the CoCoMac Database. In Proceedings of the 16th Annual Meeting of ISMRM; Toronto, Ontario, Canada. 2008b. p. 427. [Google Scholar]
- Iturria-Medina Y, et al. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage. 2007;36:645–660. doi: 10.1016/j.neuroimage.2007.02.012. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y. Sotero RC. Canales-Rodríguez EJ. Alemán-Gómez Y. Melie-García L. Studying the human brain anatomical network via diffusion-weighted MRI and Graph Theory. Neuroimage. 2008;40:1064–1076. doi: 10.1016/j.neuroimage.2007.10.060. [DOI] [PubMed] [Google Scholar]
- Johnson MD. Miocinovic S. McIntyre CC. Vitek JL. Mechanisms and Targets of Deep Brain Stimulation in Movement Disorders. Neurotherapeutics. 2008;5:294–308. doi: 10.1016/j.nurt.2008.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK. Studying connections in the living human brain with diffusion MRI. Cortex. 2008;44:936–952. doi: 10.1016/j.cortex.2008.05.002. [DOI] [PubMed] [Google Scholar]
- Leichnetz GR. Astruc J. The efferent projections of the medial prefrontal cortex in the squirrel monkey (Saimiri sciureus) Brain Res. 1976;109:455–472. doi: 10.1016/0006-8993(76)90027-5. [DOI] [PubMed] [Google Scholar]
- Lowe MJ, et al. Resting state sensorimotor functional connectivity in multiple sclerosis inversely correlates with transcallosal motor pathway transverse diffusivity. Hum Brain Mapp. 2008;29:818–827. doi: 10.1002/hbm.20576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado A. Rezai AR. Kopell BH. Gross RE. Sharan AD. Benabid A. Deep brain stimulation for Parkinson's disease: surgical technique and perioperative management. Mov Disord. 2006;21:S247–S258. doi: 10.1002/mds.20959. [DOI] [PubMed] [Google Scholar]
- McIntyre CC. Hahn PJ. Network perspectives on the mechanisms of deep brain stimulation. Neurobiol Dis. 2010;38:329–337. doi: 10.1016/j.nbd.2009.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC. Savasta M. Kerkerian-Le Goff L. Vitek JL. Uncovering the mechanism(s) of action of deep brain stimulation: activation, inhibition, or both. Clin Neurophysiol. 2004;115:1239–1248. doi: 10.1016/j.clinph.2003.12.024. [DOI] [PubMed] [Google Scholar]
- Miocinovic S, et al. Experimental and theoretical characterization of the voltage distribution generated by deep brain stimulation. Exp Neurol. 2009;216:166–176. doi: 10.1016/j.expneurol.2008.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modha DS. Singh R. Network architecture of the long-distance pathways in the macaque brain. PNAS. 2010;107:13485–13490. doi: 10.1073/pnas.1008054107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morecraft RJ, et al. Localization of arm representation in the corona radiata and internal capsule in the non-human primate. Brain. 2002;125:176–198. doi: 10.1093/brain/awf011. [DOI] [PubMed] [Google Scholar]
- Mori S. Crain BJ. Chacko VP. van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Morris DM. Embleton KV. Parker GJ. Probabilistic fibre tracking: differentiation of connections from chance events. Neuroimage. 2008;42:1329–1339. doi: 10.1016/j.neuroimage.2008.06.012. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Oroz MC, et al. Bilateral deep brain stimulation in Parkinson's disease: a multicentre study with 4 years follow-up. Brain. 2005;128:2240–2249. doi: 10.1093/brain/awh571. [DOI] [PubMed] [Google Scholar]
- Sakaie KE. Lowe MJ. An objective method for regularization of fiber orientation distributions derived from diffusion-weighted MRI. Neuroimage. 2007;34:169–176. doi: 10.1016/j.neuroimage.2006.08.034. [DOI] [PubMed] [Google Scholar]
- Saleem KS. Logothetis NK. A Combined MRI and Histology Atlas of the Rhesus Monkey Brain in Stereotaxic Coordinates. London, UK: Academic Press; 2006. [Google Scholar]
- Skudlarski P. Jagannathan K. Calhoun VD. Hampson M. Skudlarska BA. Pearlson G. Measuring brain connectivity: diffusion tensor imaging validates resting state temporal correlations. Neuroimage. 2008;43:554–561. doi: 10.1016/j.neuroimage.2008.07.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Stephan KE. Kamper L. Bozkurt A. Burns GA. Young MP. Kötter R. Advanced database methodology for the collation of connectivity data on the macaque brain (CoCoMac) Philos Trans R Soc Lond B Biol Sci. 2001;356:1159–1186. doi: 10.1098/rstb.2001.0908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan EV. Zahr NM. Rohlfing T. Pfefferbaum A. Fiber tracking functionally distinct components of the internal capsule. Neuropsychologia. 2010;48:4155–4163. doi: 10.1016/j.neuropsychologia.2010.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka J. Thalamic projections of the dorsomedial prefrontal cortex in the rhesus monkey (Macaca mulatta) Brain Res. 1976;110:21–38. doi: 10.1016/0006-8993(76)90206-7. [DOI] [PubMed] [Google Scholar]
- Tournier JD. Calamante F. Gadian DG. Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage. 2004;23:1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Tournier JD. Calamante F. Gadian DG. Connelly A. Probabilistic Fibre Tracking Through Regions Containing Crossing Fibres. In Proceedings of the 13th Annual Meeting of ISMRM; Miami, Florida, USA. 2005. p. 1343. [Google Scholar]
- Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Tuch DS. Reese TG. Wiegell MR. Makris N. Belliveau JW. Wedeen VJ. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med. 2002;48:577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- Xu W. Miocinovic S. Zhang J. Baker K. McIntyre CC. Vitek JL. Dissociation of motor symptoms during deep brain stimulation of the subthalamic nucleus in the region of the internal capsule. Exp Neurol. 2010;228:294–297. doi: 10.1016/j.expneurol.2010.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada K. Diffusion tensor tractography should be used with caution. PNAS. 2009;106:E14. doi: 10.1073/pnas.0812352106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeterian EH. Pandya DN. Prefrontostriatal connections in relation to cortical architectonic organization in rhesus monkeys. J Comp Neurol. 1991;312:43–67. doi: 10.1002/cne.903120105. [DOI] [PubMed] [Google Scholar]
- Zarei M. Johansen-Berg H. Jenkinson M. Ciccarelli O. Thompson AJ. Matthews PM. Two-dimensional population map of cortical connections in the human internal capsule. J Magn Reson Imaging. 2007;25:48–54. doi: 10.1002/jmri.20810. [DOI] [PMC free article] [PubMed] [Google Scholar]