Abstract
Purpose: The authors previously reported on a three-dimensional computer-generated breast phantom, based on empirical human image data, including a realistic finite-element based compression model that was capable of simulating multimodality imaging data. The computerized breast phantoms are a hybrid of two phantom generation techniques, combining empirical breast CT (bCT) data with flexible computer graphics techniques. However, to date, these phantoms have been based on single human subjects. In this paper, the authors report on a new method to generate multiple phantoms, simulating additional subjects from the limited set of original dedicated breast CT data. The authors developed an image morphing technique to construct new phantoms by gradually transitioning between two human subject datasets, with the potential to generate hundreds of additional pseudoindependent phantoms from the limited bCT cases. The authors conducted a preliminary subjective assessment with a limited number of observers (n = 4) to illustrate how realistic the simulated images generated with the pseudoindependent phantoms appeared.
Methods: Several mesh-based geometric transformations were developed to generate distorted breast datasets from the original human subject data. Segmented bCT data from two different human subjects were used as the “base” and “target” for morphing. Several combinations of transformations were applied to morph between the “base’ and “target” datasets such as changing the breast shape, rotating the glandular data, and changing the distribution of the glandular tissue. Following the morphing, regions of skin and fat were assigned to the morphed dataset in order to appropriately assign mechanical properties during the compression simulation. The resulting morphed breast was compressed using a finite element algorithm and simulated mammograms were generated using techniques described previously. Sixty-two simulated mammograms, generated from morphing three human subject datasets, were used in a preliminary observer evaluation where four board certified breast radiologists with varying amounts of experience ranked the level of realism (from 1 = “fake” to 10 = “real”) of the simulated images.
Results: The morphing technique was able to successfully generate new and unique morphed datasets from the original human subject data. The radiologists evaluated the realism of simulated mammograms generated from the morphed and unmorphed human subject datasets and scored the realism with an average ranking of 5.87 ± 1.99, confirming that overall the phantom image datasets appeared more “real” than “fake.” Moreover, there was not a significant difference (p > 0.1) between the realism of the unmorphed datasets (6.0 ± 1.95) compared to the morphed datasets (5.86 ± 1.99). Three of the four observers had overall average rankings of 6.89 ± 0.89, 6.9 ± 1.24, 6.76 ± 1.22, whereas the fourth observer ranked them noticeably lower at 2.94 ± 0.7.
Conclusions: This work presents a technique that can be used to generate a suite of realistic computerized breast phantoms from a limited number of human subjects. This suite of flexible breast phantoms can be used for multimodality imaging research to provide a known truth while concurrently producing realistic simulated imaging data.
Keywords: breast cancer, medical imaging, phantom, simulation, modeling, morphing
INTRODUCTION
The landscape of breast cancer imaging is constantly evolving with the introduction of novel imaging modalities, improved algorithms, and multimodality and data fusion imaging techniques.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 New imaging methods require several iterations of preclinical and clinical studies to evaluate and optimize their performance; these studies can be both time consuming and costly.
Computerized breast phantoms22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43 offer a cost-effective and practical approach to breast cancer imaging research because of their ability to produce realistic data and simulate the variability of human anatomy, which allows researchers to quantitatively optimize parameters without exposing patients to unnecessary radiation or time consuming procedures. Our group has previously presented a methodology to generate three-dimensional breast phantoms from human subject data. The phantoms include a realistic compression simulation model and are capable of simulating multimodality imaging data.31, 32, 33, 42, 43, 44, 45 The computerized breast phantoms generated from our project are a hybrid of the two phantom generation techniques, combining empirical data with flexible computer graphics techniques. They are based on dedicated breast computed tomography datasets (bCT) of human subjects,2, 3, 4 thus encompassing the variability and complexity of real human anatomy, and by using computer-graphics techniques they also have the flexibility intrinsic in a mathematical phantom.31, 32, 33, 43 However, to date, these phantoms have been based on a small cohort of human subjects, constraining the breast variability that an imaging phantom ideally possesses. The goal of this current effort was to utilize image morphing in order to generate multiple realistic phantoms from a limited set of bCT data.
Image morphing is a technique used to construct new images by gradually transitioning between two sets of images. This is done by applying geometric transformations that generate distorted datasets. There have been numerous morphing techniques developed for the computer graphics field and the medical imaging field that can be used to deform images, for example: mesh warping, field morphing, multidimensional spline deformation, energy minimization, and free-form deformations.46, 47, 48, 49, 50, 51, 52, 53 The deformation can be applied to the image data, or to finite element or surface meshes generated from the image data.
The concept of producing new datasets by deforming and morphing CT data is not new.54, 55 There have been efforts to generate supplementary datasets for clinicians to analyze during training. Deformation and morphing of real human images allow for the simulation of a diversity of disease states to complement the available data for study. In addition, deformation and morphing techniques are already used for medical image registration to perform temporal change assessments and for multimodality registration.49, 56, 57 However, to our knowledge this is the first report of producing new breast phantom datasets by deforming and morphing clinical bCT datasets of human subjects.
A basic deformation and morphing method employing mesh warping on the bCT image data is described herein. Mesh warping is a method that uses two images: a “base” image (IB) and a “target” image (IT). Both images have a mesh associated with them, referred to as MB and MT, respectively. MB specifies the coordinates of the control points used in IB, and MT specifies their corresponding positions in IT. MB and MT are used to generate a spatial transformation that maps all points from IB onto IT. Several different MT meshes can be generated that change the deformation of MB, which result in several unique realizations of a deformed and morphed IB. Although some deformation and morphing can be minor, we demonstrated previously31 that changing the structure of the phantom slightly can greatly affect the mechanical response of the breast during simulated compression and the resulting appearance of the simulated images. Therefore, a basic deformation can make a large impact in generating new and unique datasets.
This work presents a technique that can be used to generate a large number of computerized breast phantoms based on empirical data from a limited number of human subjects. However, the utility of a phantom is primarily dependent on how realistic the resulting anatomical data appear. Therefore, a preliminary observer evaluation was subsequently conducted to illustrate the realism of simulated anatomy generated using the morphing approaches described herein. The goal of this work is to produce a suite of flexible breast phantoms that will be distributed along with the XCAT phantom package44, 45, 58 to be used for multimodality breast imaging research. This suite of phantoms should make practical, large technology optimization trials by providing a known truth while concurrently producing reasonably realistic simulated imaging data of a large number of simulated subjects.
MATERIALS AND METHODS
The dedicated bCT datasets that provided the human subject basis for this work were provided by Dr. Boone's group at UC Davis2, 3, 4 and segmented with a technique that has been described in detail previously.31, 32, 33 The segmented datasets of two different human subjects were used as the “base” and “target” for deformation and morphing to generate new morphed data. The segmented datasets consisted of 300 coronal slices (each 384 × 384 voxels) with 500 μm isotropic resolution and contained three different tissue types: fat, glandular, and skin. Multiple image deformation and morphing strategies were implemented: glandular translation, breast rotation, glandular tissue rotation, glandular tissue displacement, glandular tissue erosion, morphing between breast shapes, and morphing between glandular structures. The level and complexity of the morph was user defined and then automatically executed using MATLAB R2007a (The Mathworks, Inc., Natick, MA) to perform all deformation and morphing functions.
Initial shape transformation
The initial transformations involved simple changes to the shape and orientation of the “target” breast by rotating the “target” breast or making the shell of the “target” breast wider or narrower. A mask of the “target” breast was generated to encompass the outer bounds of the breast data. Erosion and dilation of coronal slices of the “target” breast mask using a disk structuring element with a radius of 2 pixels (1 mm) was done to shrink or grow the diameter of the morphed breast data mask. The “imrotate” function, which rotates an image around its center point, was used on the coronal slices of the “target” mask to rotate the shell of the morphed breast by a user defined angle. Angles chosen for this study were 0°, 45°, 60°, and 75°. The shape- and orientation-transformed data became the new “target” data for transformative mesh generation.
Transformative mesh generation
The original “base” and “target” breasts differed in their overall size, shape, and orientation; thus it was necessary to generate a transformative mesh to map between the “base” dataset and the “target” dataset in order to produce the morphed data. These meshes provided a three-dimensional series of points of correspondence within the volumes of the breast phantoms to transfer information in the “base” breast to that in the “target” breast. The methods to do this transformative mapping differed between the sagittal and coronal planes.
The transformation in the sagittal (chest-to-nipple) direction was determined through a mapping of the coronal slice number of the “base” breast data to that of the “target” breast data in which every slice in the “base” data was mapped to a slice in the “target” data. If the “target” data chest-to-nipple distance was greater than that of the “base’ breast data, there would be “target” slices that would not have any “base” slice mapped to it; these intermediary slices were interpolated to be a linear combination of the nearest defined slices, as described in the mapping step [Eqs. 1, 2].
FS = First Slice; LS = Last Slice
| (1) |
| (2) |
In the case where the “target” chest-to nipple distance was less than that of the “base” breast data, there would be multiple coronal slices in the ‘base” data that map to a single slice in the “target” data. In such a case, for simplicity, we chose a single slice from the base, the slice farthest from the chest wall, to be mapped to the “target” slice.
The transformation in the coronal plane was determined using a radial mesh that was generated for both the “base” and the “target” data (Fig. 1). The center of each coronal slice was determined by using the halfway point between the outer bounds of the coronal breast slice. The breast diameter through the center and across a coronal slice of the “base” breast was divided into 50 uniform segments. This was repeated for each breast diameter at 0.5° increments (angular diameter) for 180° to fully cover the breast data and form the mesh of radial control points. The corresponding angular diameters of the “target’ breast were also divided into 50 segments to form a “target” mesh. Different strategies to morph the “base” breast data were implemented by changing the spacing of the control points in the “target” mesh as described below and illustrated in Fig. 1.
Figure 1.
Radial grid patterns for mesh generation. This figure illustrates how the radial grids implement mapping from the “base” to the “target” in order to implement deformations. (a) “base” breast radial grid; (b) “target” breast radial grid (direct translation); (c) “target” breast radial grid (glandular data translation – stretch toward edge); (d) “target” breast radial grid (glandular data translation – shrink toward center); (e) “target” breast radial grid (nonuniform skewing).
Mesh deformation and morphing techniques
Direct translation of coronal data
If the uniformly spaced control points on each angular diameter of the “base” data slice were mapped directly to the uniformly spaced control points on each corresponding angular diameter of the “target” data slice, this was called a direct translation of the coronal data. This method was used to shift the breast tissue to fit into the shell of the “target” breast, without changing the general structure of the tissue. This method essentially placed the breast tissue from the “base” data into the shell of the “target” data.
Shape morphing
In order to generate phantoms of intermediate shapes beyond the simple initial shape transformation described in Sec. 2A above, the shape of the morphed breast could also be based on a combination of the “base” and “target” datasets. The user was able to define at what intermediate stage between the “base” and “target” data to set the shape of the morphed breast. This was done by comparing the length of each angular diameter from the “base” data with the length of the corresponding angular diameter of the “target” data. A user defined fraction, F, was used to define how long the new length of the morphed angular diameter would be between the two datasets. For example, if F = 0.5, and the angular diameter of the “base” was 100 units long and the angular diameter of the “target” was 140 units long, the new length of the morphed angular diameter would be 120 units long. In this study we used several different F values: 0.2, 0.4, and 0.5.
Glandular data translation
For each angular diameter in the “target” data, if the user wanted to translate the tissue of the “base” breast toward the edges of the “target” breast, the control points of the “target” mesh could be defined closer together near the edges of the breast and farther apart in the center [Fig. 1c]. If the user wanted to contract the data to be closer to the center of the breast, the “target” control points could be spread out more on the edges and more closely spaced near the center [Fig. 1d]. The spacing of the control points on each angular diameter of the “target” data was low-pass filtered with a moving average filter to smooth any sharp transitions from the translation parameters. The “target” control points were mapped to the uniformly spaced mesh control points on the corresponding angular diameter of the “base” data.
Nonuniform skewing of the coronal data
The amount of translation of the glandular data in each coronal slice could be specified in a way that would nonuniformly skew the tissue so that it was not an overall translation, but a smoothly varying targeted change that was distributed throughout the different angular diameters (a). A normal probability distribution function was defined with a user specified orientation angle (μ) and a user specified standard deviation (σ) that was used to spread the change across the adjacent angular diameters,
| (3) |
The spacing of the “target” control points on each angular diameter of the “target” data was low-pass filtered to smooth any sharp transitions from the skewing parameters. The skewed grid control points on each angular diameter in the “target” data were mapped to the uniformly spaced grid control points on the corresponding angular diameter of the “base” data. In this study, mean angles of 15°, 60°, and 170° and standard deviations of 30 and 50 were used. Figure 1e demonstrates how the nonuniform skewing results in a modification of the radial grid pattern in the “target” breast data.
Rotation of glandular data
The glandular data could also be rotated by a user defined angle (ω) separately from the overall rotation of the breast described in the initial shape transformation step described above. The translation and nonuniform skewing, described above, mapped the “base” control points on one angular diameter to the control points on the corresponding angular diameter of the “target.” In order to rotate the glandular data in the coronal slice, we simply mapped the “base” control points on one angular diameter to the control points on a noncorresponding angular diameter that was offset from the “base” by ω. Offset angles for this study were 0°, 15°, 40°, 45°, and 75°.
Mapping
For each coronal slice in the “base” data, a uniform radial mesh of control points was generated and mapped to a radial mesh of control points on the “target” data (Fig. 1). The translation from the “base” to the “target” mesh was extrapolated across the “target” breast data in the coronal slice corresponding to the coronal slice in the “base” data using MATLAB's “griddata” function, which interpolates scattered data, with the linear interpolation option specified. Mapping provided the new 3D coordinate location in the morphed data for each breast voxel in the “base” data.
Tissue deformation
During tissue deformation, the mapping specified through the prior step was used to place the segmented value of the voxel from the “base” data into its new location in the morphed dataset. In the cases where the chest to nipple distance of the “target” was larger than the base, resulting in coronal slices without a direct mapping from the base, the translation maps of the two defined coronal slices on either side (sagittally) were linearly interpolated to generate a translation for the undefined slice.
There may not have been a one-to-one mapping of the “base” data voxels to the morphed data; therefore, steps were taken to generate nonsparse structures. A mask of the “base” data was morphed and used to create a mask of the morphed data that was used to define both the fat and the skin. The coronal slice of the morphed data mask was morphologically closed with a disk structuring element of radius 10 pixels (5 mm). It was also then closed in the sagittal and transverse planes using a disk structuring element of radius 3 pixels (1.5 mm). To remove any extraneous spots or holes, the “bwmorph” “majority” function, which sets a pixel to be 1 or 0 if five or more pixels in its 3 × 3 neighborhood are 1s or 0s, respectively, was used over all the anatomical planes as well.
The altered glandular data underwent a similar set of steps to generate nonsparse glandular structures; however, the “bwmorph” “fill” operation, which changes individual 0s that are surrounded by 1s into 1s, was used first and then followed by a morphological closing using a disk structuring element with a radius of 1 pixel (500 μm). These steps allow the altered glandular tissue to maintain small structures and holes in the glandular tissue, instead of generating a large contiguous block.
Combining the glandular tissue of the “base” and “target” data
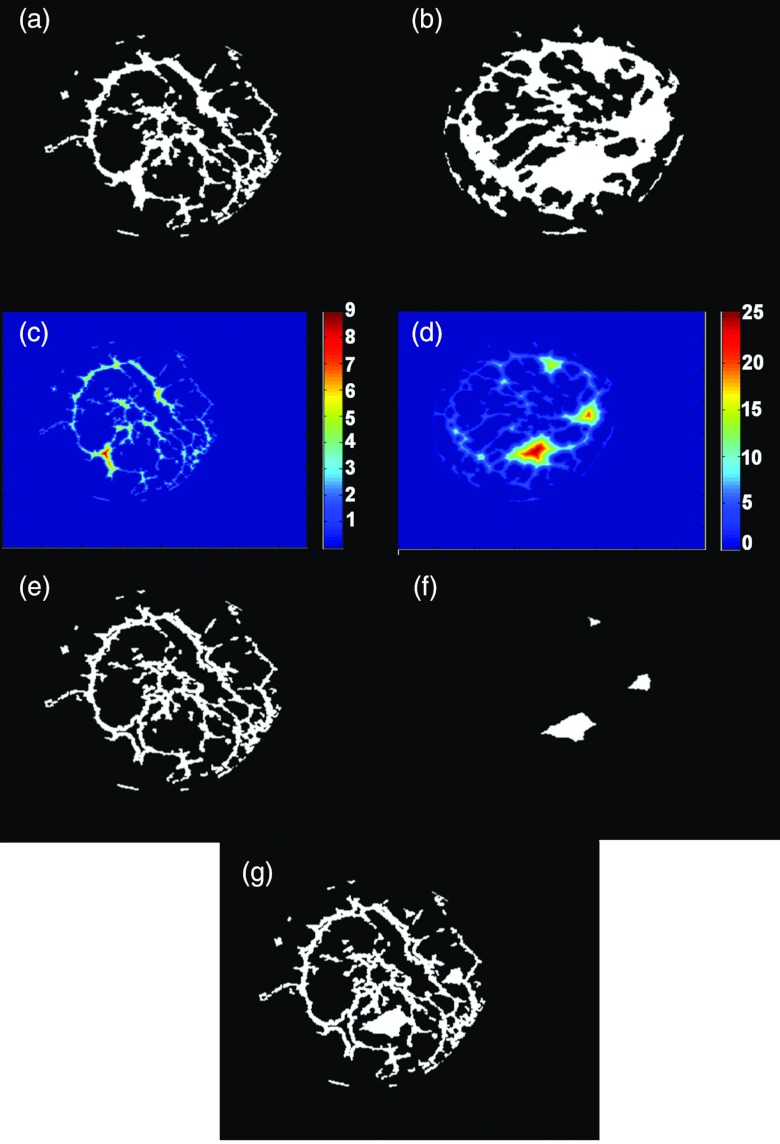
To generate morphed breasts with glandular tissue that resulted from a combination of the “base” and “target” data, a distance transform was applied to the glandular tissue of the newly generated morphed data and the “target” data's glandular tissue. The “bwdist” function, which calculates the Euclidean distance transform of a binary image, was used to separate the glandular tissue in terms of its Euclidean distance from other tissues. For example, a value of 1 would be immediately adjacent (within 500 μm) to fat or skin in any direction, and a value of 10 would be 10 voxels (5 mm) away from fat or skin in any direction. The maximum distance (dmax) of the glandular tissue for each coronal slice in both the morphed data and the “target” data was used to determine the threshold for each dataset by a user defined fraction (f) of dmax. The threshold for each dataset was applied in each coronal slice such that for one dataset, glandular voxels with distance values that were 1 to f × dmax_1 were used, and in the other dataset, voxels with distance values f × dmax_2 to dmax_2 were used. Values of f used in this study were 0.2 and 0.5. In order to ensure that there were no extraneous spots or holes, the new combinatorial glandular tissue was morphologically closed in all anatomical planes with a disk structuring element of radius 1 pixel (500 μm). While this technique did not guarantee the realistic continuity of structures between coronal slides, it allowed for the unique combination of smaller glandular structures from one dataset with the larger structures from the other dataset. Figure 2 is a demonstration of the process used to combine the glandular tissue from the base and target breast data.
Figure 2.
Demonstration of the combination of glandular tissue from two different breasts. (a) Binary coronal slice from the “base” breast; (b) binary coronal slice from the “target’ breast; (c) distance transform image from the “base” breast; (d) distance transform image from the “target” breast; (e) smaller structures chosen from the “base” breast; (f) larger structures chosen from the “target” breast; (g) morphed breast glandular data resulting from the combination of the “base” and “target” breasts glandular data.
Erosion of glandular tissue
Following the completion of morphing the glandular tissue, the user could also make the glandular tissue thinner. The sagittal and transverse planes were subject to erosion by a disk structuring element of radius 1 pixel (500 μm). Following erosion, the coronal planes were morphologically closed with the same disk structuring element.
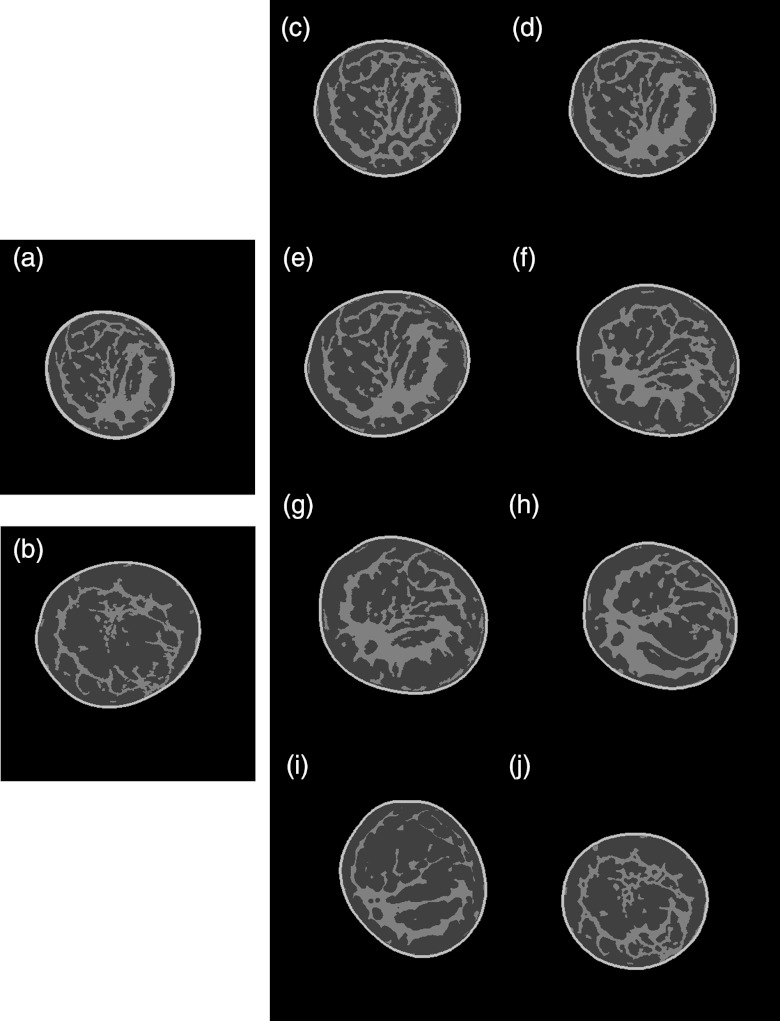
Figure 3 gives a demonstration of the effects of specific deformations described in Secs. 2A, 2B, 2C, 2D, 2E, 2F, 2G above on actual human subject breast phantom data, and illustrates visually the impact of these mathematical transformations.
Figure 3.
Sample coronal slices showing the effects of specific deformations. (a) Coronal slice from the “base” breast; (b) coronal slice from the “target” breast; (c) scaling the “base” breast glandular tissue to fit into the shell of the “target” breast; (d) scaling the “base” breast glandular tissue and fitting it into a resized shell of the “target” breast; (e) scaling and rotating the “base” breast glandular tissue and fitting it into the shell of the target breast; (f) scaling the “base” breast glandular tissue and fitting it into a rotated shell of the target breast; (g) scaling the “base” breast glandular tissue using the glandular data translation function to shrink the tissue toward the center of the “target” breast shell; (h) scaling and nonuniformly skewing the “base” breast glandular tissue and fitting it into the “target” breast shell; (i) scaling and eroding the “base” breast glandular tissue and fitting it into the “target” breast shell; (j) combining the “base” breast glandular tissue smaller structures with the “target” breast glandular tissue larger structures and fitting it into the “target” breast shell; and (k) combining the “target” breast glandular tissue smaller structures with the “base” breast glandular tissue larger structures and fitting it into the “target” breast shell.
Sagittal extension of the glandular tissue
In some cases, the different morphing methods may not have produced glandular tissue that reached the nipple. However, knowing that anatomically there should be a ductal network that branches off from the nipple, we developed a simple method to extend the glandular tissue to the farthest coronal slice from the chest wall, which was assumed to be the nipple. The glandular data in the last coronal slice that contained glandular data were assumed to be part of the ductal network, so it was morphologically dilated using a disk structuring element of radius 1 pixel (500 μm) to allow the glandular tissue to slowly grow toward the nipple. From the last slice of glandular data until the farthest coronal slice from the chest wall, every other coronal slice was dilated and the in-between slices were simply a copy of the preceding slice. While not a realistic ductal network, this ensured that each slice contained glandular data, and the assumed nipple in the morphed breast was connected to its glandular tissue.
Skin and fat assignment
In order to generate a layer of skin that was 2 mm thick,31, 33 coronal slices of the mask of the morphed breast were eroded by a disk structuring element of radius 4 pixels (2 mm). The eroded mask was then assigned to the fat region and the 2 mm thick eroded layer surrounding the fat was assigned to skin.
Glandular density assignment
Only the morphed glandular tissue that overlapped with the fat region (the region interior to the bounded skin line) was used to define the glandular tissue of the complete morphed data. The morphed dataset was interpolated out to 300 coronal images (each 768 × 768 voxels) with an in-plane resolution of 250 μm and slice thickness of 500 μm, in order to be used for tissue assignment after compression. The glandular data of the large morphed dataset was divided into three different densities33 to be used during the image generation step. This density differentiation process was previously found to more closely emulate the compositional marbling effect in clinical data where glandular and adipose tissues are interspersed in varying degrees.33 However, since there was no original bCT data to base the density groupings on, the distance transform (using “bwdist”) was applied to rank the glandular tissue according to Euclidean distance from other tissue. The distances were sorted in ascending order and the lowest half was assigned to the lowest density level, half to three-quarters of the maximum distance was assigned to the middle density level, and the highest quarter of distances was assigned to the highest density level. This technique was chosen because this trend was observed in the segmented human data.
Simulated FEM compression and image generation
Methods previously described31, 32, 33 were used to generate a tetrahedral mesh from the morphed data with 2.5 mm elements. Compression of the morphed breast was simulated using finite element methods (FEM). The modulus ratio (Fat:Glandular:Skin) chosen for the tissues was set to 1:10:88, the Poisson's ratio was set to 0.49, a coefficient of friction of 0.46 was used for the skin, and the breasts were all compressed to 5 cm thickness. The compressed tetrahedral model was assigned tissue values according to the large morphed dataset produced in the “glandular density assignment” step, and then translated into a subdivision surface model. As described in detail previously,33, 44 a simulated projection of the compressed morphed breast phantom was generated directly on the mesh model using a technique developed by Segars et al.44 with attenuation coefficients for the different tissues derived from the International Commission on Radiation Units and Measurements tissue data.59 Thus, while the datasets used for morphing were voxelized, the simulated images generated from the morphed phantoms following compression used defined mesh surfaces fit to the morphed and FEM compressed data rather than voxelized data to simulate projection images through the volume. Images were simulated with 1000 × 1000 pixels at 250 μm resolution. A sigmoid correction function was applied to the projection in order to simulate the grayscale properties of a screen-film mammogram.
Experimental evaluation—Preliminary observer rankings
To provide a preliminary estimate of the realism of images generated using the suite of breast phantoms described above, a preliminary subjective assessment was performed with a limited number of observers using a 10 point scale to assess realism where 1 was defined as “fake,” 5 as “somewhat real,” and 10 as “real.” The images were graded in terms of the realism of displayed breast parenchyma and not on the image viewing platform as the images were displayed on personal computers with limited resolution through an online album. In order to generate images for review, three original, unmorphed, breast datasets were used as the “base” and “targets” for deformation and morphing to generate 59 new datasets. The original datasets were chosen from subjects that had three different volumetric breast density levels: 14%, 28%, and 38%.
Sixty-two total simulated cranio-caudal (CC) mammograms were generated, with three images generated from breast phantoms created directly from the bCT data without deformation or morphing and 59 images generated from different combinations of deformation and morphing of the original datasets as detailed above. Results were analyzed for morphed and unmorphed groups separately, in order to ascertain if the estimated realism was noticeably degraded following the deformation techniques. Four board certified breast radiologists with varying amounts of experience (7, 16, 19, and 37 years) provided their rankings. The radiologists viewed all simulated mammograms on a web image viewer (www.Jalbum.com) with the viewing environment limited by standard web resolution and personal computer settings. Although the web format was a simple and easy way for the radiologists to quickly review the simulated images, the viewer did not provide any user controls to adjust contrast, window or level.
RESULTS
Deformation and morphing
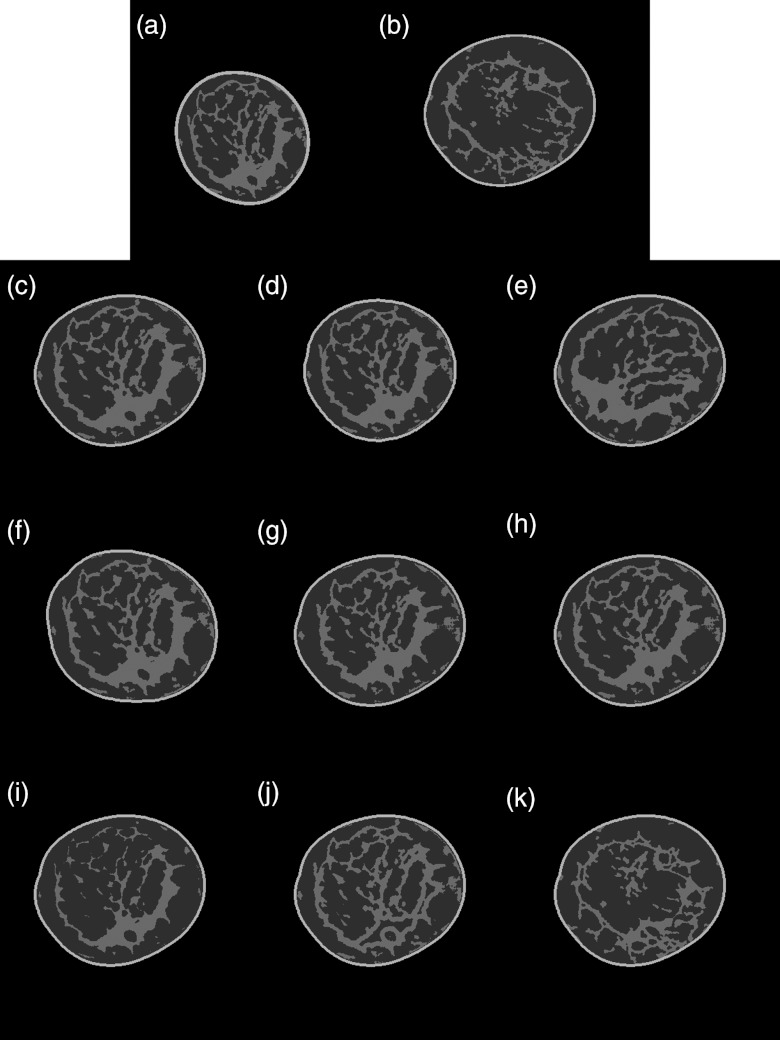
Figure 4 illustrates what coronal slices from the new, segmented datasets look like after implementing a number of different combinations of deformation and morphing techniques, including translation, nonlinear skewing, shape changes, rotation of either breast shell or glandular tissue, and morphing between the breasts. All of these coronal slices subjectively demonstrated glandular tissue definition and connectivity that were similar to that of the unmorphed datasets, and showed placement of glandular tissue with respect to the skin line roughly comparable to that of the unmorphed cases.
Figure 4.
Sample slices showing how combining different deformations affects the size, shape, and glandular distribution of the newly created morphed breast phantoms. (a) Coronal slice from the “base” breast; (b) coronal slice from the “target” breast; (c) combining the “base” breast glandular tissue smaller structures with the “target” breast glandular tissue larger structures and fitting it into a smaller “target” breast shell; (d) directly translating the “base” breast tissue into a resized smaller “target” breast shell; (e) directly translating the “base” breast tissue into the “target” breast shell; (f) rotating, nonlinearly skewing, and shrinking the “base” tissue toward the center of the “target” breast shell and combining with the larger structures of the “target” breast tissue; (g) rotating and shrinking the “base” breast tissue toward the center of the “target” breast shell and rotating the “target” breast shell; (h) rotating and nonlinearly skewing the “base” breast tissue, and then fitting it into a rotated and resized smaller “target” breast shell; (i) rotating and eroding the “base” breast glandular tissue and fitting it into a rotated and resized “target” breast shell; and (j) combining the “target” breast tissue smaller structures with the larger structures of the “base” breast and fitting it into a resized “base” breast shell.
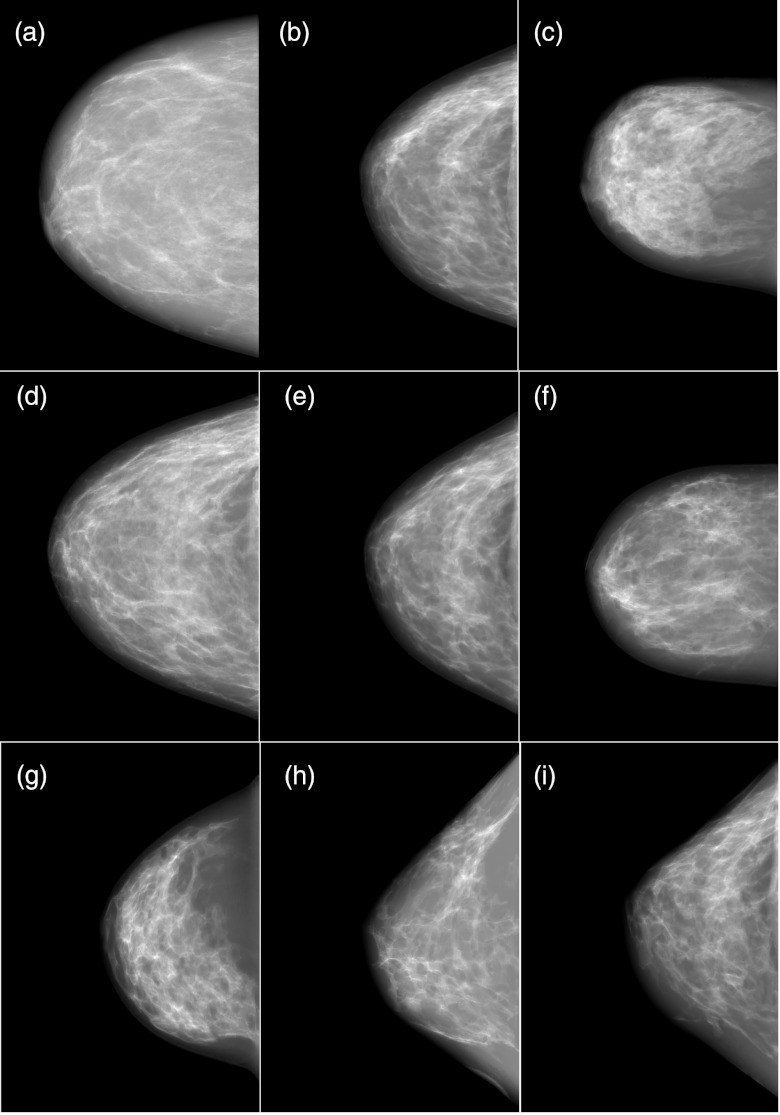
Figure 5 contains simulated mammograms generated using three datasets of original, unmorphed, segmented bCT data and six new datasets that were morphed or deformed versions of the three original datasets using methods described above.
Figure 5.
Simulated CC mammograms ranging from realism rankings of 6–8. (a) 14% dense original breast – median score 6; (b) 28% dense original breast – median score 7.5; (c) 38% dense original breast – median score 6.5; (d) deformed/morphed (a) and (b) - key morphing parameters were shape morphing and glandular combination – median score 7.5; (e) deformed/morphed (a) and (b) - key morphing parameters were erosion and glandular combination – median score 8; (f) deformed/morphed (a) and (c) - key morphing parameters were 75° rotation, erosion, and glandular combination – median score 8; (g) deformed/morphed (b) and (c) - key morphing parameters were shape morphing and 60° rotation – median score 7; (h) deformed/morphed (a) and (b) - key morphing parameters were erosion, nonuniform skew, and 60° rotation – median score 6; (i) deformed/morphed (b) and (c) - key morphing parameters were rotation, erosion, and glandular combination – median score 6.5.
Experimental evaluation—Preliminary observer rankings
The breast radiologists who reviewed the simulated mammographic images generated from the suite of 62 breast phantoms provided comments and rankings. The average realism ranking across all radiologists for all 62 images was 5.87 ± 1.99. Three of the four observers had overall average rankings of 6.89 ± 0.89, 6.9 ± 1.24, 6.76 ± 1.22, whereas the fourth observer ranked both morphed and unmorphed images noticeably lower than the other observers, with an overall average of 2.94 ± 0.7. Individual radiologist rankings for unmorphed and morphed phantom images are shown in Tables 1, 2, respectively. There was no significant difference (p value: 0.82) between the realism rankings of the unmorphed datasets, which were based on original human subject data, and the morphed datasets, which resulted from utilizing the morphing methodology presented in this work that morphs two original datasets. The individual radiologists had p values for differences between the unmorphed and morphed datasets ranging from 0.41 to 0.89. Thus, in this very limited initial evaluation of “realism,” the rankings indicated that three of the observers rated both the unmorphed and morphed datasets midway between “somewhat real” and “real,” with no significant difference between the groups. The fourth observer showed no significant difference between the groups but rated both unmorphed and morphed groups as midway between “fake” and “somewhat real.”
Table 1.
Experimental evaluation of unmorphed phantom realism.
| Radiologist 1 | Radiologist 2 | Radiologist 3 | Radiologist 4 | |
|---|---|---|---|---|
| Average ± standard deviation | 6.67 ± 0.58 | 7.0 ± 1.0 | 7.33 ± 1.15 | 3.0 ± 0.0 |
| Minimum | 6 | 6 | 6 | 3 |
| Maximum | 7 | 8 | 8 | 3 |
| Median | 7 | 7 | 8 | 3 |
Table 2.
Experimental evaluation of morphed phantom realism.
| Radiologist 1 | Radiologist 2 | Radiologist 3 | Radiologist 4 | |
|---|---|---|---|---|
| Average ± standard deviation | 6.9 ± 0.9 | 6.9 ± 1.26 | 6.73 ± 1.23 | 2.93 ± 0.72 |
| Minimum | 5 | 2 | 4 | 1 |
| Maximum | 9 | 9 | 10 | 5 |
| Median | 7 | 7 | 7 | 3 |
The radiologists commented that all of the simulated cases were of “scattered tissue or heterogeneously dense” breasts and none were “fatty replaced or extremely dense.” They also commented that the “images look very good to excellent on the whole,” some looked “really realistic,” and that “almost all cases have appropriate distribution of tissue.” The lowest ranking images had large areas of homogenous fat that does not typically appear in real images and “needed more texture” or appeared “more blurred or smudgy.”
DISCUSSION
The morphing and deformation techniques implemented in this work demonstrate the ability to generate new and unique imaging phantoms that can be used for breast imaging research. Although the level of deformation was primarily through simple transformations using rotation, translation, or small alterations in the size and shape of the breast tissue; these small changes affect the morphology of the breast and its mechanical response to finite element compression, which ultimately affects the simulated images generated from the phantoms. In this current version of the technique, all deformations and parameters were user selected and then automatically executed, however future iterations could automate the entire process.
There are several options that can change the resulting morphed data to produce a large number of unique simulated phantoms, including: choice of the “base” and “target” datasets, rotation angles, size changes, fraction choices, size, and shape of structuring elements, FEM parameter choices (for mammographic simulations), and breast density allocation percentages. The large number of variables allows for a flexible breast phantom that can generate numerous phantom realizations using a limited number of human subject datasets.
This paper presents a proof of concept of the methodologies developed to produce these breast phantoms, but not a formal evaluation of the phantoms in the context of any particular imaging modality. In order to demonstrate the resulting anatomy of the morphed phantoms, we showed the phantoms in application to mammography, but these same simulated breast phantoms can also be used as research tools in CT, nuclear medicine, MR imaging, and ultrasound, by the inclusion of modeling of those respective imaging systems. One limitation of the current work is that our demonstration of “realism” was primarily aimed toward evaluating the breast phantom anatomy itself and not so much toward the specific modeling of a given imaging system. Thus, we generated simulated mammographic projections to do a preliminary evaluation of the “realism” of the morphed phantoms compared with the unmorphed phantoms, but with a very minimalistic approach to simulating the mammographic system. We used sophisticated FEM methods to simulate breast compression but only simple ray-tracing to produce the simulated projection mammograms shown to the observers. We did not include all of the system-related factors that can affect final mammographic appearance, including modeling of the detector system MTF, correlated noise power spectrum, x-ray scatter, and focal spot blurring. The absence of these components of system modeling might well have accounted for some of the overall “realism” score when compared to actual mammograms (especially for observer 4 who recorded low scores for both morphed and unmorphed datasets). However, it is unlikely that these factors would have substantially affected the relative “realism” of the morphed versus unmorphed datasets, which was the primary end point of this primarily methodological work. In the future, large-scale observer studies using these phantoms must include a proper and careful modeling of all of the components of a given imaging system to reflect observer performance indicative of what would be obtained clinically.
There were other issues that were not addressed in the present work that will be the subject of future investigations. One of the major issues in deciding on the morphing variables was predicting how realistic the resulting datasets or simulated images would be. We tried to maintain a similar tissue distribution as the “base” and “target” images for the morphed datasets in order to preserve the level of realism provided by the original data. However, a smoothly varying, shape-based, transition between the glandular tissues of the “base” and “target” datasets was not attempted because of the complexity of the tissue, most notably the disparate distribution of the glandular tissue between different subjects. Consequently, the combination of the dissimilar glandular tissues may have resulted in a morphed dataset that contained structures that would never occur in human subjects. Therefore, computational anatomy methods, which can handle both the growth and atrophy of tissue, can be investigated to generate more realistic transitions between the ‘base” and ‘target” dataset.60 Computational anatomy methods can also be explored to refine the glandular density of the breast phantom to a user defined level, which would be an important area for future investigation since breast density is known to influence the detectability of breast cancer, and this would be a useful tool to employ for research with the breast phantom package. Supplementary breast structures such as tumors, microcalcifications, Cooper's ligaments, or lobules could be computer generated and added to the phantoms. These structures were not available in the segmented data, either because the data was based on normal breast tissue or because the structures were difficult to visualize and segment from the original bCT images. These added components would allow the phantoms to simulate different levels of health or disease and also prevent homogenous regions of fat in the phantom, which is important since that was a primary source of unrealistic simulated images from the preliminary observer evaluation. In addition, there remains the possibility of generating an inestimable number of new morphed datasets utilizing different combinations of the morphing techniques presented in this study. Therefore, it would be useful to perform a parametric analysis to determine the morphing techniques that produce the most compelling and realistic phantoms.
The preliminary observer evaluation rankings suggest that the methodology described may be a feasible means of producing adequately realistic breast phantoms for a number of observer tests requiring a large dataset of simulated human data. However, there are several important limitations to the current preliminary evaluation of “realism” described in this paper. First, the numbers of observers and phantoms in this preliminary evaluation were small, and it will clearly be necessary to conduct further studies with larger numbers of subjects and unmorphed and morphed breast phantoms. Second, the relative imbalance in the number of unmorphed and morphed cases shown to the observers may result in bias in estimating statistical significance of any difference. We believe any bias will likely disfavor rather than favor our morphed image sets because it is unlikely that morphed datasets will show better “realism” than unmorphed datasets. Nonetheless, future larger scale studies should include a larger number of unmorphed datasets (which are in limited supply currently) in order to minimize this source of any potential bias. Third, it will be necessary to conduct future larger studies with access for all observers to standardized high-quality viewing monitors. Fourth, it will be important to include sample training datasets to calibrate the observers to the phantom appearance.
Feedback from observers in this current study will enable us to refine the set of parameters used to generate the larger datasets used in future studies. Three observers had average collective rankings of 7.00 and 6.84 for unmorphed and morphed datasets, respectively, but the fourth observer rankings were notably lower at 3.00 and 2.93, respectively, indicating different interpretations of the ranking scale or standard to which to compare realism. This was most likely due to miscommunication or misinterpretation of the purpose of the study, which was to evaluate the realism of the displayed breast parenchyma and not the quality of the image viewing platform. The fourth observer commented that “…given the limitations of the reading conditions. They are of course easily recognized as breasts but do not look to me like a good quality mammogram.” We suspect that the fourth observer interpreted the purpose of the study differently than the other observers and held the simulated images to a higher standard of quality and did not evaluate the images based on the realism of the phantom structure but instead on image quality, which would be limited by standard web resolution as well as their own personal computer display. This underscores the need to clarify the purpose of the study and provide a uniform reading environment for future observers with clearly outlined objectives in order to calibrate the realism ranking. The range of responses for observers will need to be elucidated in further evaluations of these phantoms in future larger observer studies.
CONCLUSIONS
We have described a methodology to generate a suite of unique breast phantoms from a limited number of dedicated bCT datasets by using a combination of mesh deformation and morphing techniques. To our knowledge, this is the first presentation of deformation and morphing of dedicated bCT data from different subjects to create new morphed datasets. This suite of breast phantoms provides a mechanism that potentially enables a large scale clinical evaluation of multimodality breast imaging data. Future efforts will include more advanced morphing techniques to improve on the presented deformation and morphing methods; a parametric analysis of the effect and performance of different morphing practices; as well as a comprehensive user study to evaluate the level of realism achieved with a suite of computerized breast phantoms. The suite of phantoms presented in this work may provide an important tool to optimize, evaluate, and improve new and existing breast imaging techniques and devices.
ACKNOWLEDGMENTS
The authors would like to thank Dr. John Boone and his lab at UC Davis Medical Center for providing the dedicated breast CT data that was used for this work. The authors are also grateful to the breast radiologists who provided their rankings: Dr. Jay Baker, Dr. Sujata Ghate, Dr. Roberta Jong, and Dr. Kalesha Hack. Finally, the authors would like to thank Dr. Joseph Lo for his assistance with image analysis and interpretation. This work has been supported by the Department of Defense Breast Cancer Research Program (W81XWH-06-1-0732) and National Institutes of Health NIH/NCI (R01CA134658), NIH/NIBIB (R01EB001838), NIH/NCI (R01CA112437), NIH/NCI (R01CA94236).
References
- Berg W. A., Blume J. D., Cormack J. B., Mendelson E. B., Lehrer D., Bohm-Velez M., Pisano E. D., Jong R. A., Evans W. P., Morton M. J., Mahoney M. C., Hovanessian Larsen L., Barr R. G., Farria D. M., Marques H. S., and Boparai K., for the ACRIN 6666 Investigators, “Combined screening with ultrasound and mammography vs mammography alone in women at elevated risk of breast cancer,” J. Am. Med. Assoc. 299, 2151–2163 (2008). 10.1001/jama.299.18.2151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boone J. M., Kwan A. L., Yang K., Burkett G., Lindfors K. K., and Nelson T. R., “Computed tomography for imaging the breast,” J. Mammary Gland Biol. Neoplasia 11, 103–111 (2006). 10.1007/s10911-006-9017-1 [DOI] [PubMed] [Google Scholar]
- Lindfors K. K., Boone J. M., Newell M. S., and D’Orsi C. J., “Dedicated breast computed tomography: The optimal cross-sectional imaging solution?,” Radiol. Clin. North Am. 48, 1043–1054 (2010). 10.1016/j.rcl.2010.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindfors K. K., Boone J. M., Nelson T. R., Yang K., Kwan A. L., and Miller D. F., “Dedicated breast CT: Initial clinical experience,” Radiology 246, 725–733 (2008). 10.1148/radiol.2463070410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brem R. F., Fishman M., and Rapelyea J. A., “Detection of ductal carcinoma in situ with mammography, breast specific gamma imaging, and magnetic resonance imaging: A comparative study,” Acad. Radiol. 14, 945–950 (2007). 10.1016/j.acra.2007.04.004 [DOI] [PubMed] [Google Scholar]
- Fang Q., Selb J., Carp S. A., Boverman G., Miller E. L., Brooks D. H., Moore R. H., Kopans D. B., and Boas D. A., “Combined optical and x-ray tomosynthesis breast imaging,” Radiology 258, 89–97 (2011). 10.1148/radiol.10082176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glick S. J., “Breast CT,” Annu. Rev. Biomed. Eng. 9, 501–526 (2007). 10.1146/annurev.bioeng.9.060906.151924 [DOI] [PubMed] [Google Scholar]
- Gur D., Abrams G. S., Chough D. M., Ganott M. A., Hakim C. M., Perrin R. L., Rathfon G. Y., Sumkin J. H., Zuley M. L., and Bandos A. I., “Digital breast tomosynthesis: Observer performance study,” Am. J. Roentgenol. 193, 586–591 (2009). 10.2214/AJR.08.2031 [DOI] [PubMed] [Google Scholar]
- Kriege M., Brekelmans C. T. M., Boetes C., Besnard P. E., Zonderland H. M., Obdeijn I. M., Manoliu R. A., Kok T., Peterse H., Tilanus-Linthorst M. M. A., Muller S. H., Meijer S., Oosterwijk J. C., Beex L. V. A. M., Tollenaar R. A. E. M., de Koning H. J., Rutgers E. J. T., Klijn J. G. M., and G. the Magnetic Resonance Imaging Screening Study, “Efficacy of MRI and mammography for breast-cancer screening in women with a familial or genetic predisposition,” N. Engl. J. Med. 351, 427–437 (2004). 10.1056/NEJMoa031759 [DOI] [PubMed] [Google Scholar]
- Kuhl C. K., Schrading S., Leutner C. C., Morakkabati-Spitz N., Wardelmann E., Fimmers R., Kuhn W., and Schild H. H., “Mammography, breast ultrasound, and magnetic resonance imaging for surveillance of women at high familial risk for breast cancer,” J. Clin. Oncol. 23, 8469–8476 (2005). 10.1200/JCO.2004.00.4960 [DOI] [PubMed] [Google Scholar]
- Madhav P., Crotty D. J., McKinley R. L., and Tornai M. P., “Initial development of a dual-modality SPECT-CT system for dedicated mammotomography,” IEEE Nuclear Science Symposium Conference Record, Vol. 4 (IEEE, 2006), pp. 2382–2386. 10.1109/NSSMIC.2006.354392 [DOI]
- Pisano E. D., Gatsonis C., Hendrick E., Yaffe M., Baum J. K., Acharyya S., Conant E. F., Fajardo L. L., Bassett L., D’Orsi C., Jong R., and Rebner M., “Diagnostic performance for digital versus film mammography for breast-cancer screening,” N. Engl. J. Med. 353, 1773–1783 (2005). 10.1056/NEJMoa052911 [DOI] [PubMed] [Google Scholar]
- Pisano E. D., Hendrick R. E., Yaffe M. J., Baum J. K., Acharyya S., Cormack J. B., Hanna L. A., Conant E. F., Fajardo L. L., Bassett L. W., D’Orsi C. J., Jong R. A., Rebner M., Tosteson A. N. A., and Gatsonis C. A., DMIST Investigators Group, “Diagnostic accuracy of digital versus film mammography: Exploratory analysis of selected population subgroups in DMIST,” Radiology 246, 376–383 (2008). 10.1148/radiol.2461070200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saslow D., Boetes C., Burke W., Harms S., Leach M. O., Lehman C. D., Morris E. A., Pisano E. D., Schnall M. D., Sener S., Smith R. A., Warner E., Yaffe M., Andrews K. S., and Russell C. A., “American Cancer Society Guidelines for Breast Screening with MRI as an Adjunct to Mammography,” Ca-Cancer J. Clin. 57, 75–89 (2007). 10.3322/canjclin.57.2.75 [DOI] [PubMed] [Google Scholar]
- Schilling K., Conti P., Adler L., and Tafra L., “The role of positron emission mammography in breast cancer imaging and management,” Appl. Radiol. 37, 26–36 (2008). [Google Scholar]
- Sinha S. P., Roubidoux M. A., Helvie M. A., Nees A. V., Goodsitt M. M., LeCarpentier G. L., Fowlkes J. B., Chalek C. L., and Carson P. L., “Multi-modality 3D breast imaging with x-ray tomosynthesis and automated ultrasound,” in Proceedings of the 29th Annual International Conference of the IEEE EMBS (IEEE, 2007). [DOI] [PubMed]
- Yibao W., Kai Y., Packard N., Lin F., Stickel J., Vi-Hoa T., Jinyi Q., Boone J. M., Cherry S. R., and Badawi R. D., “Characteristics of the PET component of a dedicated breast PET/CT scanner prototype,” IEEE Nuclear Science Symposium Conference Record, Vol. 4 (IEEE, 2006), pp. 2335–2339.
- Lee C. H., Dershaw D. D., Kopans D., Evans P., Monsees B., Monticciolo D., Brenner R. J., Bassett L., Berg W., Feig S., Hendrick E., Mendelson E., D’Orsi C., Sickles E., and Burhenne L. W., “Breast cancer screening with imaging: Recommendations from the society of breast imaging and the ACR on the use of mammography, breast MRI, breast ultrasound, and other technologies for the detection of clinically occult breast cancer,” J. Am. Coll. Radiol. 7, 18–27 (2010). 10.1016/j.jacr.2009.09.022 [DOI] [PubMed] [Google Scholar]
- Le-Petross H. T. and Shetty M. K., “Magnetic resonance imaging and breast ultrasonography as an adjunct to mammographic screening in high-risk patients,” Semin. Ultrasound CT MR 32, 266–272 (2011). 10.1053/j.sult.2011.03.005 [DOI] [PubMed] [Google Scholar]
- Madhav P., Crotty D. J., McKinley R. L., and Tornai M. P., “Evaluation of tilted cone-beam CT orbits in the development of a dedicated hybrid mammotomograph,” Phys. Med. Biol. 54, 3659 (2009). 10.1088/0031-9155/54/12/004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafer C. M., Samei E., and Lo J. Y., “The quantitative potential for breast tomosynthesis imaging,” Med. Phys. 37, 1004–1016 (2010). 10.1118/1.3285038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakic P., Albert M., Brzakovic D., and Maidment A., “Mammogram synthesis using a 3D simulation. I. Breast tissue model and image acquisition simulation,” Med. Phys. 29, 2131–2139 (2002). 10.1118/1.1501143 [DOI] [PubMed] [Google Scholar]
- Bakic P., Albert M., Brzakovic D., and Maidment A., “Mammogram synthesis using a 3D simulation. II. Evaluation of synthetic mammogram texture,” Med. Phys. 29, 2140–2151 (2002). 10.1118/1.1501144 [DOI] [PubMed] [Google Scholar]
- Bakic P., Albert M., Brzakovic D., and Maidment A., “Mammogram synthesis using a three-dimensional simulation. III. Modeling and evaluation of the breast ductal network,” Med. Phys. 30, 1914–1925 (2003). 10.1118/1.1586453 [DOI] [PubMed] [Google Scholar]
- Bakic P. R., Zhang C., and Maidment A. D. A., “Development and characterization of an anthropomorphic breast software phantom based upon region-growing algorithm,” Med. Phys. 38, 3165–3176 (2011). 10.1118/1.3590357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bliznakova K., Bliznakov Z., Bravou V., Kolitsi Z., and Pallikarakis N., “A three-dimensional breast software phantom for mammography simulation,” Phys. Med. Biol. 48, 3699–3719 (2003). 10.1088/0031-9155/48/22/006 [DOI] [PubMed] [Google Scholar]
- Bliznakova K., Suryanarayanan S., Karellas A., and Pallikarakis N., “Evaluation of an improved algorithm for producing realistic 3D breast software phantoms: Application for mammography,” Med. Phys. 37, 5604–5617 (2010). 10.1118/1.3491812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen B., Shorey J., R. S.SaundersJr., Richard S., Thompson J., Nolte L. W., and Samei E., “An anthropomorphic breast model for breast imaging simulation and optimization,” Acad. Radiol. 18, 536–546 (2011). 10.1016/j.acra.2010.11.009 [DOI] [PubMed] [Google Scholar]
- Gong X., Glick S. J., Liu B., Vedula A. A., and Thacker S., “A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis, and cone-beam CT breast imaging,” Med. Phys. 33, 1041–1052 (2006). 10.1118/1.2174127 [DOI] [PubMed] [Google Scholar]
- Hoeschen C., Fill U., Zankl M., Panzer W., Regulla D., and Dohring W., “A high-resolution voxel phantom of the breast for dose calculations in mammography,” Radiat. Prot. Dosim. 114, 406–409 (2005). 10.1093/rpd/nch558 [DOI] [PubMed] [Google Scholar]
- Hsu C. M. L., Palmeri M. L., Segars W. P., Veress A. I., and J. T.DobbinsIII, “An analysis of the mechanical parameters used for finite element compression of a high-resolution 3D breast phantom,” Med. Phys. 38, 5756–5770 (2011). 10.1118/1.3637500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C. M., Segars W. P., Lo J. Y., Veress A. I., Boone J. M., and J. T.DobbinsIII, “Three-dimensional computer generated breast phantom based on empirical data,” Proc. SPIE 6913, 691314 (2008). 10.1117/12.772185 [DOI] [Google Scholar]
- Li C. M., Segars W. P., Tourassi G. D., Boone J. M., and J. T.DobbinsIII, “Methodology for generating a 3D computerized breast phantom from empirical data,” Med. Phys. 36, 3122–3131 (2009). 10.1118/1.3140588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma A. K. W., Gunn S., and Darambara D. G., “Introducing DeBRa: A detailed breast model for radiological studies,” Phys. Med. Biol. 54, 4533–4545 (2009). 10.1088/0031-9155/54/14/010 [DOI] [PubMed] [Google Scholar]
- O’Connor J., Das M., Didier C., Mah’D M., and Glick S., “Comparison of two methods to develop breast models for simulation of breast tomosynthesis and CT,” Proc. IWDM ’08 International Workshop on Digital Mammography (Springer-Verlag, Berlin, 2008), pp. 417–425. 10.1007/978-3-540-70538-3_58 [DOI]
- O’Connor J., Das M., Didier C., Mah'd M., and Glick S., “Development of an ensemble of digital breast object models,” Proc. IWDM ’10 International Workshop on Digital Mammography (Springer-Verlag, Berlin, 2010), pp. 54–61. 10.1007/978-3-642-13666-5_8 [DOI]
- O’Connor J. M., Das M., Didier C., Mah’D M., and Glick S. J., “Using mastectomy specimens to develop breast models for breast tomosynthesis and CT breast imaging,” Proc. SPIE 6913, 691315 (2008). 10.1117/12.772666 [DOI] [Google Scholar]
- Shorey J., “Stochastic simulations for the detection of objects in three dimensional volumes: Applications in medical imaging and ocean acoustics,” Ph.D. dissertation, Duke University, 2007. [Google Scholar]
- Zhou L., Oldan J., Fisher P., and Gindi G., “Low-contrast lesion detection in tomosynthetic breast imaging using a realistic breast phantom,” Proc. SPIE 6142, 61425A (2006). 10.1117/12.652343 [DOI] [Google Scholar]
- Zyganitidis C., Bliznakova K., and Pallikarakis N., “A novel simulation algorithm for soft tissue compression,” Med. Biol. Engin. Comput. 45, 661–669 (2007). 10.1007/s11517-007-0205-y [DOI] [PubMed] [Google Scholar]
- Mahr D. M., “Three-dimensional, in silico breast phantom for multimodality image simulations,” M.S. thesis, University of Illinois at Urbana-Champaign, Bioengineering, 2009. [Google Scholar]
- Hsu C. M. L., “Three-dimensional computerized breast phantom based on empirical data,” Ph.D. dissertation, Duke University, 2010. [Google Scholar]
- Li C. M., Segars W. P., Lo J. Y., Veress A. I., Boone J. M., and J. T.DobbinsIII, “Computerized 3D breast phantom with enhanced high-resolution detail,” Proc. SPIE 7258, 72580S (2009). 10.1117/12.813529 [DOI] [Google Scholar]
- Segars W. P., Mahesh M., Beck T. J., Frey E. C., and Tsui B. M. W., “Realistic CT simulation using the 4D XCAT phantom,” Med. Phys. 35, 3800–3808 (2008). 10.1118/1.2955743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segars W. P., Sturgeon G., Mendonca S., Grimes J., and Tsui B. M. W., “4D XCAT phantom for multimodality imaging research,” Med. Phys. 37, 4902–4915 (2010). 10.1118/1.3480985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolberg G., “Image morphing: A survey,” Visual Comput. 14, 360–372 (1998). 10.1007/s003710050148 [DOI] [Google Scholar]
- Davis M. H., Khotanzad A., Flamig D. P., and Harms S. E., “A physics-based coordinate transformation for 3D image matching,” IEEE Trans. Med. Imaging 16, 317–328 (1997). 10.1109/42.585766 [DOI] [PubMed] [Google Scholar]
- Rueckert D., Sonoda L. I., Hayes C., Hill D. L. G., Leach M. O., and Hawkes D. J., “Nonrigid registration using free-form deformations: application to breast MR images,” IEEE Trans. Med. Imaging 18, 712–721 (1999). 10.1109/42.796284 [DOI] [PubMed] [Google Scholar]
- Pluim J. P. W., Maintz J. B. A., and Viergever M. A., “Mutual-information-based registration of medical images: A survey,” IEEE Trans. Med. Imaging 22, 986–1004 (2003). 10.1109/TMI.2003.815867 [DOI] [PubMed] [Google Scholar]
- Brock K. K., Sharpe M. B., Dawson L. A., Kim S. M., and Jaffray D. A., “Accuracy of finite element model-based multi-organ deformable image registration,” Med. Phys. 32, 1647–1659 (2005). 10.1118/1.1915012 [DOI] [PubMed] [Google Scholar]
- Guo Y., Sivaramakrishna R., Lu C.-C., Suri J., and Laxminarayan S., “Breast image registration techniques: A survey,” Med. Biol. Eng. Comput. 44, 15–26 (2006). 10.1007/s11517-005-0016-y [DOI] [PubMed] [Google Scholar]
- Lee S.-Y., Chwa K.-Y., Hahn J., and Shin S. Y., “Image morphing using deformation techniques,” J. Visualization Comput. Animat. 7, 3–23 (1996). [DOI] [Google Scholar]
- Roose L., Mollemans W., Loeckx D., Maes F., and Suetens P., “Biomechanically based elastic breast registration using mass tensor simulation,” Proc. Med. Image Comput. Comput.-Assist. Interv. MICCAI 2006 (Springer, 2006), pp. 718–725. [DOI] [PubMed]
- Bergeron B. P., Sato L., and Rouse R. L., “Morphing as a means of generating variation in visual medical teaching materials,” Comput. Biol. Med. 24, 11–18 (1994). 10.1016/0010-4825(94)90033-7 [DOI] [PubMed] [Google Scholar]
- Krol A., Unlu M. Z., Baum K. G., Mandel J. A., Lee W., Coman I. L., Lipson E. D., and Feiglin D. H., “MRI/PET nonrigid breast-image registration using skin fiducial markers,” Phys. Medica 21, 39–43 (2006). 10.1016/S1120-1797(06)80022-0 [DOI] [PubMed] [Google Scholar]
- Maes F., Collignon A., Vandermeulen D., Marchal G., and Suetens P., “Multimodality image registration by maximization of mutual information,” IEEE Trans. Med. Imaging 16, 187–198 (1997). 10.1109/42.563664 [DOI] [PubMed] [Google Scholar]
- Maintz J. B. A. and Viergever M. A., “A survey of medical image registration,” Med. Image Anal. 2, 1–36 (1998). 10.1016/S1361-8415(01)80026-8 [DOI] [PubMed] [Google Scholar]
- Segars W. P. and Tsui B., “MCAT to XCAT: The evolution of 4D computerized phantoms for imaging research,” Proc. IEEE 97, 1954–1968 (2009). 10.1109/JPROC.2009.2022417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- U. S. Natl. Bur. Stand, Report of the task group on reference man: Anatomical values for reference man, 1975.
- Miller M. I., “Computational anatomy: Shape, growth, and atrophy comparison via diffeomorphisms,” NeuroImage 23, S19–S33 (2004). 10.1016/j.neuroimage.2004.07.021 [DOI] [PubMed] [Google Scholar]