Figure 4.
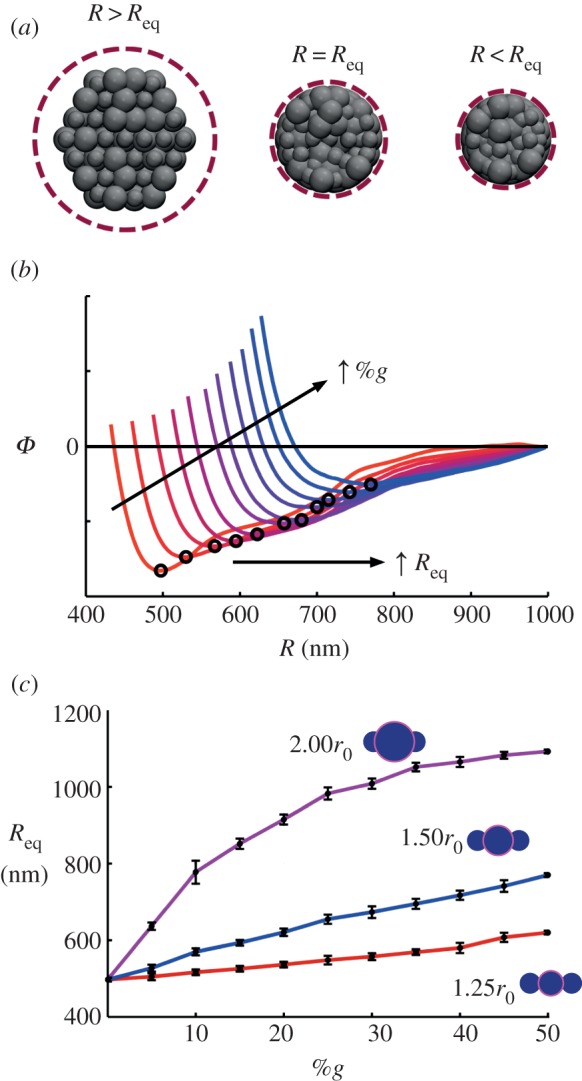
Attaining equilibrium (stress-free) fibre radii, Req. (a) Depiction of fibre cross section upon equilibration, subject to cylindrical compression. For a confining volume of R > Req, the fibrils maintain a configuration close to the initial hexagonal arrangement. To attain an equilibrated structure (R = Req), the cylinder decreases radius at a constant rate, and the potential energy (ϕ) of the fibre system is tracked to determine a minimum. (b) Representative plot of potential energy versus confining cylinder (e.g. fibre) radius, R, for rg = 1.50r0, %g from 5% to 50%. The equilibrium radius, Req, is then taken as the minimum of the energy–radius curve (indicated). As anticipated, there is a constant increase in equilibrium radii with increasing globules, but is irregular due to the random distribution. Moreover, the magnitude of the energetic minimum decreases with an increase in %g. (c) Results for three globule sizes, all %g distributions. Error bars indicate statistical distribution for three model samples. (Online version in colour.)
