Figure 9.
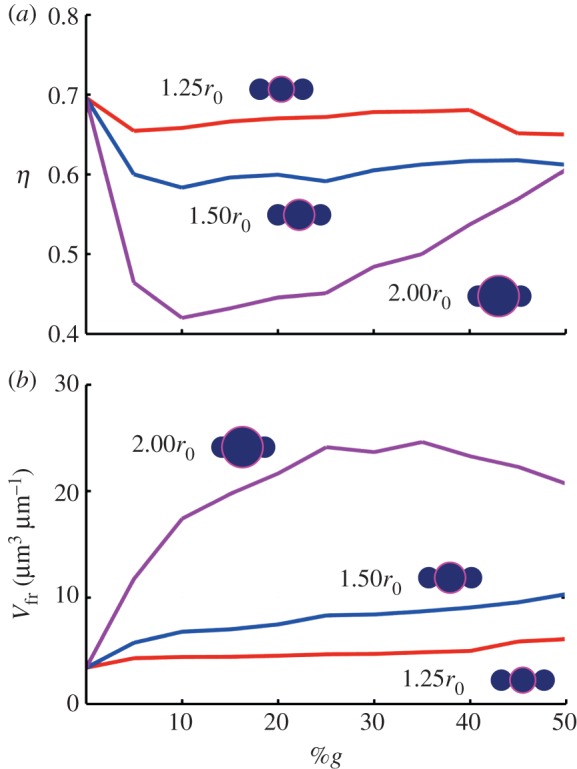
Fibril packing efficiency (η) and fibre free volume (Vfr). Beyond metrics of strength, the addition of globules also effect the geometrical character of the fibres. (a) Plot of volume fraction (η; a measure of packing efficiency; see equation (3.2)) versus %g. Note the highest packing efficiency at 0%g (η ≈ 0.7), where the fibrils are the most compact owing to their uniformity. The addition of larger globules results in less efficient packing. Indeed, owing to the imposed connectivity of the particulates, they cannot arrange freely in the most efficient manner. For both rg = 1.25r0 and 1.50r0, the packing efficiency is near-constant, regardless of %g (with η ≈ 0.67±0.01 and η ≈ 0.60±0.01, respectively). For rg = 2.0r0, however, we see a large drop in packing efficiency owing to the large required equilibrium radius with the addition of a few globules (η ≈ 0.44 at 10%g). The subsequent addition of globules enhance the packing, effectively filling the wasted space, but the discrepancy between globule and fibril radii leads to relatively inefficient packing (and thus less fibril interaction) even at high %g (η ≈ 0.63 at 50%g). (b) Plot of free volume versus %g. Available free volume may facilitate the known process of supercontraction [70–73], whereby absorbed water leads to significant shrinkage in an unrestrained silk fibre [12,73,74]. To trigger supercontraction, solvent must penetrate the fibre, enhanced by the presence of fibril globules due to an increase in free volume (and thus exposed surface area). The free volume is normalized by the length of the fibril to attain volume per length (μm3 μm−1). Correspondingly, we see large available free volume for rg = 2.00r0, whereas there are nominal gains for both rg = 1.25r0 and 1.50r0. (Online version in colour.)
