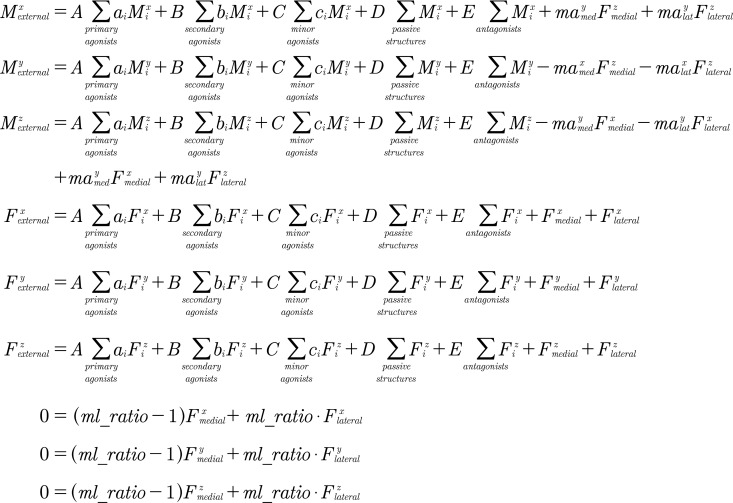Fine Tuning Total Knee Replacement Contact Force Prediction Algorithms Using Blinded Model Validation

Short abstract

The purpose of this study was to perform a blinded comparison of model predictions of total knee replacement contact forces to in vivo forces from an instrumented prosthesis during normal walking and medial thrust gait by participating in the “Third Grand Challenge Competition to Predict in vivo Knee Loads.” We also evaluated model assumptions that were critical for accurate force predictions. Medial, lateral, and total axial forces through the knee were calculated using a previously developed and validated parametric numerical model. The model uses equilibrium equations between internal and external moments and forces to obtain knee joint contact forces and calculates a range of forces at instances during the gait cycle through parametric variation of muscle activity levels. For 100 instances during a normal over-ground gait cycle, model root mean square differences from eTibia data were 292, 248, and 281 for medial, lateral, and total contact forces, respectively. For 100 instances during a medial thrust gait cycle, model root mean square differences from eTibia data were 332, 234, and 470 for medial, lateral, and total contact forces, respectively. The percent difference between measured and predicted peak total axial force was 2.89% at the first peak and 9.36% at the second peak contact force for normal walking and 3.94% at the first peak and 14.86% at the second peak contact force for medial thrust gait. After unblinding, changes to model assumptions improved medial and lateral force predictions for both gait styles but did not improve total force predictions. Axial forces computed with the model compared well to the eTibia data under blinded and unblinded conditions. Knowledge of detailed knee kinematics, namely anterior-posterior translation, appears to be critical in obtaining accurate force predictions.

Introduction

Forces at the knee joint are of major interest for both the understanding of joint disease and the design of total knee replacements (TKRs). Mathematical modeling has long been the only avenue for obtaining information about knee joint forces during walking and other activities of daily life [1,2]. Mathematical determination of knee joint forces is difficult because of mathematical indeterminacy of the knee. Paul [3] and Morrison [4] were among the first to calculate contact forces at the tibio-femoral articulation. Paul modeled the entire lower extremity and solved for as many unknowns as there were equations of motion. Morrison grouped the various muscles and ligaments around the knee joint into functional units and, thus, created a statically determinate problem. Many studies followed their example and reduced the number of unknown quantities (e.g., number of unknown muscle forces). However, since these “reduction methods” eliminate or combine muscles of similar function they cannot account for measured muscle activation or muscle co-contraction. Other approaches to overcome indeterminacy use “optimization methods.” Seireg and Arvikar [5] pioneered this approach by establishing objective functions where the sum of muscle forces and weighted sum of residual joint moments were minimized. Optimization methods are not necessarily driven by physiological criteria, which, in fact, are largely unknown. Furthermore, the objective function may be different between subject groups and vary from normal for individuals with joint pathology and/or TKRs.

Recently, in vivo force data have become available for patients implanted with instrumented TKRs [6–14]. Because these in vivo instrumented force data are limited to a small number of subjects and two implant designs, the generalizability of the data is uncertain. Further, data are only available for a few gait styles and activities. Therefore, mathematical models are still valuable for evaluating knee loads for large patient cohorts, for different knee designs, and under variable daily activities. In addition, mathematical modeling may provide more than just a data set by allowing insight into mechanistic strategies. Nonetheless, in vivo measured force data are the gold standard for mathematical model validation.

In order to advance the field of mathematical modeling, Fregly et al. [2] initiated a competition that would allow investigators to blindly validate models against measured data. The model discussed in this paper differs from previous approaches in that a parametric approach to the indeterminate problem is taken [15,16]. Muscles are categorized into groups based on their physiological function and muscle activation is parametrically varied within each group. This approach results in a statically determinate problem at the expense of precision, i.e., a range of contact forces describing a solution space rather than an exact answer is calculated for each time point due to variable muscle activation. This loss in precision is not necessarily negative, as a person may use slightly different muscle strategies from trial to trial. The solution space captures this potential variability and represents a physiological envelope of knee joint contact forces during an activity.

The purpose of this study was to expand our previous model validation work [17] by participating in the “Third Grand Challenge Competition to Predict in vivo Knee Loads” to perform a blinded validation study. We had three aims: (1) to directly compare blinded model predictions to measured in vivo forces for a single motion trial of normal over-ground gait and a single trial of medial thrust gait, (2) to determine strategies that improved our model algorithms after forces were unblinded, and (3) to apply the improved model to multiple trials of each activity and evaluate the predictions. It was hoped that these three aims would allow us to make recommendations for the modeling community and describe what knowledge is essential for accurate force prediction.

Methods

Grand Challenge Competition Data from SimTK Website.

Raw data from the “Third Grand Challenge Competition to Predict in vivo Knee Loads” was obtained from the SimTK website2 (Table 1). Specifically, we used laser scans of the femoral and tibial components of the eTibia implant, a single static trial of marker trajectories and analog force plate data, marker trajectories and analog force plate data of normal walking and medial thrust gait trials, and synchronized eTibia force files (after unblinding). The data were for a single subject (female, height 167 cm, weight 78.4 kg) with an eTibia instrumented left-side TKR. Further details of the competition data are reported in Fregly et al. [2].

Table 1.

Files used from the data available for the third grand challenge competition at https://simtk.org/home/kneeloads

Laser scans	Marker trajectories	Synchronized eTibia force files
Femoral component.stl	SC_staticfor_again1.c3d	SC_ngait_og5_knee_forces.csv
Tibial insert.stl	SC_ngait_og5.c3d	SC_ngait_og6_knee_forces.csv*
	SC_ngait_og6.c3d*	SC_ngait_og7_knee_forces.csv
	SC_ngait_og7.c3d	SC_ngait_og8_knee_forces.csv
	SC_ngait_og8.c3d	SC_ngait_og9_knee_forces.csv
	SC_ngait_og9.c3d	SC_medialthrust3_knee_forces.csv
	SC_medialthrust3.c3d	SC_medialthrust4_knee_forces.csv*
	SC_medialthrust4.c3d*	SC_medialthrust5_knee_forces.csv
	SC_medialthrust5.c3d	SC_medialthrust6_knee_forces.csv
	SC_medialthrust6.c3d	SC_medialthrust8_knee_forces.csv
	SC_medialthrust8.c3d

^* indicates competition trial.

Kinetic and Kinematic Input Data.

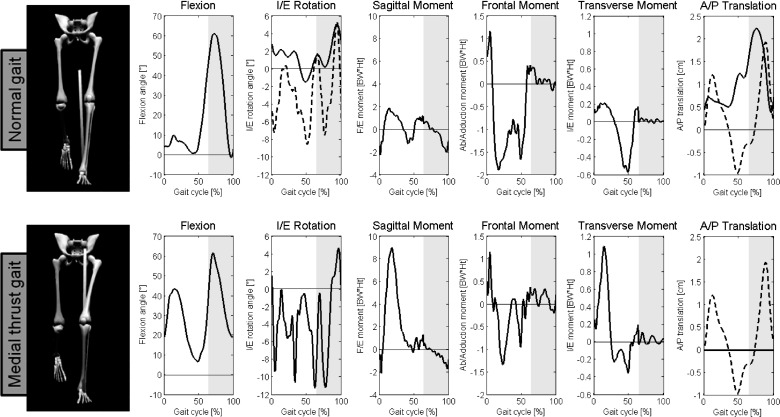
Raw motion analysis data made available for the competition were acquired using a modified Cleveland Clinic marker set [18]. To obtain inverse dynamics data from the marker trajectories, a bilateral lower limb skeletal model (The MotionMonitor, Innovative Sports Training Inc., Chicago, IL) was developed using a toes-forward static standing trial. The left and right knee joint centers were defined as the midpoint of medial and lateral static knee markers, which had been placed on the medial and lateral epicondyles of the femur. Marker trajectories and ground reaction forces were low-pass filtered before kinetic and kinematic calculation at 15 Hz and 100 Hz, respectively. The beginning and end of the gait cycle were defined as the onset of ground reaction force on two different force plates under two successive heel strikes of the left foot. Three-dimensional knee joint external moments; hip, knee, and ankle flexion angles; and knee internal-external rotation angles required for force calculations were calculated from the skeletal model, raw competition marker trajectories, and analog force plate data (Fig. 1). The path of contact between the tibial and femoral TKR components is another necessary model input and was calculated with the kinematics and previously developed software [19].

Fig. 1.

Gait kinematics and kinetics used as inputs to the parametric model were computed in MotionMonitor for normal and medial thrust gait. Solid lines show the data used in blinded model predictions. Dashed lines show the kinematics that were changed for unblinded model predictions: internal-external (I/E) rotation. and anterior-posterior (A/P) translation for normal gait, and A/P translation for medial thrust gait. Gray areas of the graph represent the swing phase. Note for blinded predictions of medial thrust gait, A/P translation was set to zero throughout the gait cycle. Units for external moments are in percent body weight times height (BW*Ht).

Calculation of TKR Contact Forces Overview.

A previously developed [15] and validated [17] parametric numerical model was used to calculate TKR contact forces. Six equilibrium equations balanced the external knee joint forces and moments with the internal forces and moments from muscles, passive structures, and contact forces for the medial and lateral aspects of the tibial plateau in a three-dimensional coordinate system. Three additional equations defined the ratio of forces between the medial and lateral aspects of the tibial plateau. With nine total equations, nine unknowns were computed: six contact force components and three muscle group activation levels (Fig. 2).

Fig. 2.

Nine equilibrium equations used to solve for 9 unknowns. $F_{\mathrm{medial}}^x$, $F_{\mathrm{lateral}}^x$, $F_{\mathrm{medial}}^y$, $F_{\mathrm{lateral}}^y$, $F_{\mathrm{medial}}^z$, and $F_{\mathrm{lateral}}^z$ are the unknown medial and lateral tibial plateau contact force components. $A$, $B$, and $C$ are the unknown muscle group activation levels. $D$ is the activation of passive structures (0 or 1). $E$ is the antagonist activation level. $M_{\mathrm{external}}^x$, $M_{\mathrm{external}}^y$, and $M_{\mathrm{external}}^z$ are the external knee joint moments, and $F_{\mathrm{external}}^x$, $F_{\mathrm{external}}^y$, and $F_{\mathrm{external}}^z$ are the external knee joint forces. $M_i^x$, $M_i^y$, and $M_i^z$ are the maximum physiological muscle moments, and $F_i^x$, $F_i^y$, and $F_i^z$ are the maximum physiological muscle forces. $a_i$, $b_i$, and $c_i$ are the parametrically varied relative muscle activation levels. ${\mathit{ma}}_{\mathrm{med}}^x$, ${\mathit{ma}}_{\mathrm{lat}}^x$, ${\mathit{ma}}_{\mathrm{med}}^y$, ${\mathit{ma}}_{\mathrm{lat}}^y$, ${\mathit{ma}}_{\mathrm{med}}^z$, ${\mathit{ma}}_{\mathrm{lat}}^z$ define the location of the contact point from the center of the medial (med) and lateral (lat) tibial plateau. $\mathit{ml}\_\mathit{ratio}$ is the ratio of medial to total contact force through the knee. $x$, $y$, and $z$: point laterally, anteriorly, and superiorly, respectively, from the center of the surface of the tibial plateau. Note that in the coordinate system a right-hand rule is used for a right knee and a left-hand rule is used for a left knee where $y$ points in the direction of walking.

All muscles crossing the knee joint that served to balance the external knee moments during a given instance of gait were categorized into three “agonist” muscle groups: primary, secondary, and minor agonists. Muscles that did not serve to balance the external knee moments in all three planes were categorized into an “antagonist” muscle group. Within each group, muscles were allowed to retain their own line of action and physiological maximum muscle force. Physiological maximum muscle forces were obtained with the knee kinematics and a musculoskeletal model modified from Delp et al. [20] and developed in OpenSim v.2.2.1 [21]. The relative activation levels of muscles within a particular group were parametrically varied from 0.1 to 1.0. An overall activation level was calculated for each agonist group by the model (three of the nine calculated unknowns). The overall activation level for the antagonist group was also parametrically varied up to 5%. The parametric variation of relative muscle activation levels resulted in a solution space or envelope of calculated knee joint forces representing different strategies a person may use while performing the activity.

Blinded (Original) Model Assumptions.

Four assumptions were needed to calculate TKR axial forces from competition data: (1) anterior-posterior knee translations, (2) the ratio of medial knee force to total knee force, (3) the contribution of passive structures to force and moment balance across the knee joint, and (4) friction. First, knee joint anterior-posterior translation was used both when calculating the path of contact between the tibia and the femur and in force calculations. Because fluoroscopic data were unavailable for the trials of interest and the provided marker set was not sensitive to translations at the knee, anterior-posterior translation was not available from the patient. In the case of normal walking we substituted anterior-posterior translation and internal-external rotation from an over-ground walking trail of TKR patient with a similar implant design [11]. The external knee joint moments of the walking trial with the substituted kinematics were similar to the competition trial. Because no analogous trial was available for medial thrust gait, anterior-posterior translation at the knee was set to zero throughout the gait cycle (Fig. 1).

Second, we assumed that the ratio between the force passing through the medial tibial plateau and the total knee force was proportional to the change in the external knee frontal plane moment as previously reported in the literature [9]. Equation (1) was used to calculate the ratio of medial force to total force, ml_ratio(t), at each percentage of the gait cycle t.

$$\mathit{ml}\_\mathrm{ratio}(t)=-\frac{0.175}{{\overline{M}}_{\max }^y-{\overline{M}}_{\min }^y}M(t){}^y+0.5$$ (1)

The mean maximum ${\overline{M}}_{max}^y$ and minimum ${\overline{M}}_{min}^y$ external frontal plane moments were obtained from the stance phases of ten steps of normal walking from the competition data. ${\overline{M}}_{max}^y$ was equal to 0.9336 Body Weights*Height and ${\overline{M}}_{min}^y$ was equal to −2.5437 Body Weights*Height. In Eq. (1), the difference between the mean maximum and mean minimum external knee frontal plane moments was scaled to 17.5% and multiplied by the external frontal plane moment $M(t){}^y$. The 0.5 intercept term assumes that frontal plane moments of zero result in equal load share between the medial and lateral tibial plateau. The equation resulted in ratios of medial to total force ranging from ∼40% to ∼65% during stance.

Third, we assumed passive structures only contributed to contact force solutions if muscles in the group with moments attributed to transverse plane equilibrium (“minor agonists,” Fig. 2) could not balance the entire external transverse plane moment. In this case, the remainder of the external transverse plane moment minus the summed minor agonists group muscle moment was assumed to be balanced by a couple moment produced by passive structures. Fourth, the dynamic coefficient between the TKR bearing surfaces was assumed to be 0.1. After the solution space was calculated, solutions resulting in shear forces that exceeded 0.1 times the axial force were excluded.

Model Assumptions After Unblinding.

Our strategy for changing the model after unblinding of instrumented forces included re-examining the four assumptions outlined above. First, we changed our original assumption that knee anterior-posterior translation was the same as that of another patient with a similar prosthesis during normal walking, and that anterior-posterior translation did not occur during medial thrust gait. Instead, we modified the average anterior-posterior translation from a subset of TKR patients with NexGen CR prostheses previously evaluated in our laboratory [22,23] for use with the competition data. An anterior-posterior translation profile was created from the profile of a subset of patients with high total anterior-posterior translation during walking gait cycles [24]. The timings of the transitions from anterior to posterior sliding directions were adjusted to correspond with the timings of zero crosses of the external sagittal plane moment from the normal walking competition trial. The same anterior-posterior translation was substituted for both normal walking and medial thrust gait trials (Fig. 1).

Second, our original scaling of the ratio between medial and total forces (Eq. (1)) was adjusted to match regressed medial and lateral contact forces from the eTibia output. Medial and lateral contact forces for both over-ground walking and medial thrust gait were calculated from unfiltered three-dimensional total forces and moments measured by the eTibia instrument using the regression equations provided by the competition. A linear regression to determine the scaling and intercept terms for Eq. (1) (previously 0.175 and 0.5, respectively) was performed between the external frontal plane knee moment and the eTibia medial to total force ratio. The regression was computed from heel strike of the left foot at the beginning of the gait cycle, into terminal stance at the percentage of the gait cycle when the right foot had a higher ground reaction force than the left foot. For over-ground normal walking, the mean amplitude of Eq. (1) was scaled to 45.76%, and the medial-lateral ratio was set at 0.6272 for zero moment (Eq. (2)). For medial thrust gait, the mean amplitude of Eq. (1) was scaled to 22.93%, and the medial-lateral ratio was set at 0.5992 for zero moment (Eq. (3)). ${\overline{M}}_{max}^y$ and ${\overline{M}}_{min}^y$ were the same (0.9336 and −2.5437, respectively).

$$\mathit{ml}\_{\mathit{ratio}}_{\genfrac{}{}{0ex}{}{\mathrm{normal}}{\mathrm{gait}}}(t)=-\frac{0.4576}{{\overline{M}}_{max}^y-{\overline{M}}_{min}^y}M(t){}^y+0.6272$$ (2)

$$\mathit{ml}\_{\mathit{ratio}}_{\genfrac{}{}{0ex}{}{\mathrm{medial}}{\mathrm{thrust}}}(t)=-\frac{0.2293}{{\overline{M}}_{max}^y-{\overline{M}}_{min}^y}M(t){}^y+0.5992$$ (3)

Third, our original assumption that passive structures only served to balance the remaining transverse plane moment after the muscles in the minor agonists group had already contributed their maximum amount was revisited. Passive structures were allowed to contribute twice the remaining transverse plane moment that muscles could not balance and either half (normal walking) or equal to (medial thrust gait) the remaining frontal plane moment that muscles could not balance. This allowed passive structures to enter into model solutions even when muscles could balance the entire moment themselves, resulting in a wider solution space at some points during gait or allowing the model to obtain solutions at instances where previously none were obtained.

Fourth, our original assumption that the coefficient of friction of 0.1 between the TKR bearing surfaces was increased to 0.2. Our assumption was that when tractive rolling (simultaneous rolling and sliding) occurs, the coefficient of friction can reach higher values up to 0.2 [25].

Reported Results.

The means of the model predicted solution space for medial, lateral, and total axial force at 100 instances during the normal walking and medial thrust gait competition trials were compared to regressed eTibia data. The model with new assumptions was also applied in a blinded fashion to four additional trials of each gait pattern. Root-mean-square (rms) deviation was calculated for total force, medial force, and lateral force between model predictions and eTibia results for the entire trials (all 100 instances). The eTibia device does not directly output medial and lateral axial forces, only total axial forces and torques. For comparison to model results, medial and lateral axial forces were regressed from the total axial force, lateral direction force, and torque about the anterior-posterior axis using a numerical model as provided by the competition [9].

Results

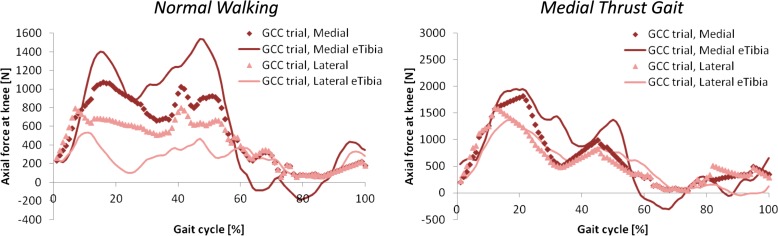
The blinded medial and lateral axial force predictions compared well to the output and regressions of the eTibia data (Fig. 3). The total axial force compared slightly better to the eTibia data than did the medial and lateral axial forces separately as shown by lower rms values (Table 2). For normal walking, total predicted axial force underestimated the eTibia data by 52 N (2.89%) at the first peak and 188 N (9.36%) at the second peak. For medial thrust gait, total predicted axial force underestimated the eTibia data by 131 N (3.94%) at the first peak and 318 N (14.86%) at the second peak. After unblinding the eTibia force data, the adjustments to model assumptions resulted in normal walking force predictions with medial and lateral magnitudes closer to those regressed from eTibia data for the competition trial (Fig. 4). rms deviation values decreased after unblinding when the medial and lateral forces were considered separately but did not change or slightly worsened for the total force (Table 2). Predictions of the medial thrust gait competition trial also improved mildly (Fig. 4).

Fig. 3.

Original blinded model predictions of axial force in the medial (dark diamonds) and lateral (light triangles) compartments of the knee compared to the regressed eTibia medial (dark line) and lateral (light line) axial forces for the normal walking and medial thrust gait competition trials. Note different y-axis scales.

Table 2.

Root-mean-square (rms) deviation values comparing model predicted axial forces to the associated measured total axial forces and regressed medial and lateral axial forces over the entire gait cycle

				Additional trials
Gait style	Side	Competition trial, unblinded	Competition trial, unblinded	Trial 1	Trial 2	Trial 3	Trial 4
Normal walking	Medial	292	238	148	187	192	227
	Lateral	248	100	144	121	90.8	114
Total	281	293	208	258	218	300
Medial thrust gait	Medial	332	351	310	238	268	250
	Lateral	234	200	200	186	143	194
Total	470	473	423	367	311	370

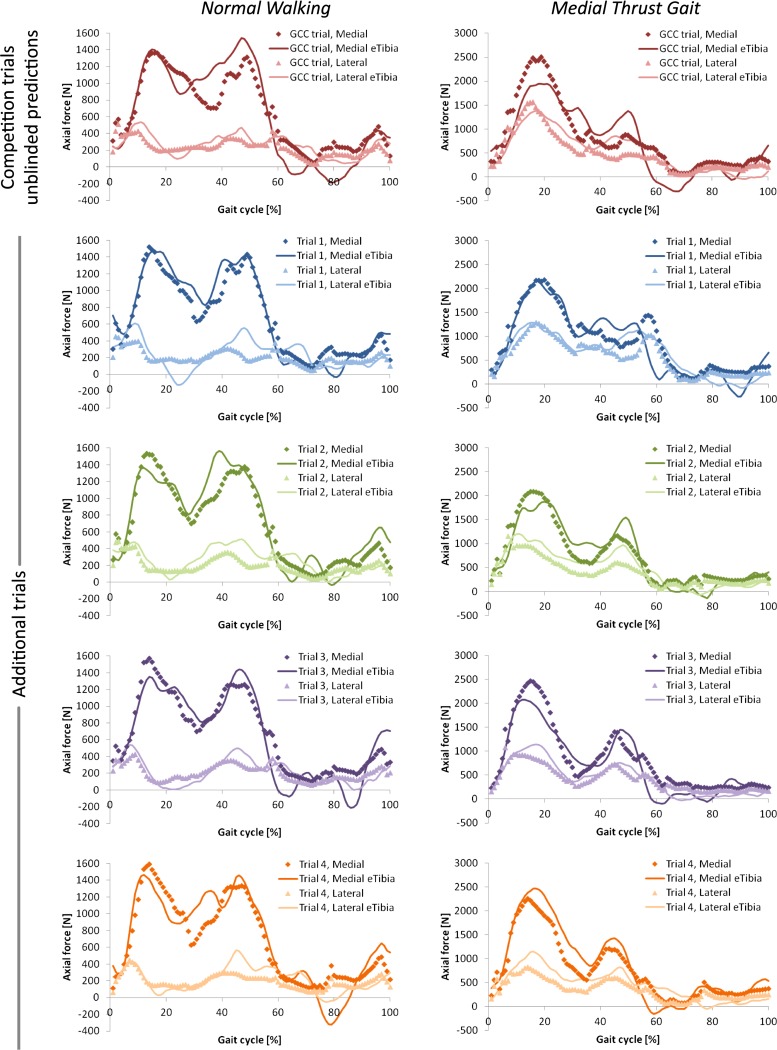
Fig. 4.

Unblinded model predictions of axial force in the medial (dark diamonds) and lateral (light triangles) compartments of the knee compared to the regressed eTibia medial (dark line) and lateral (light line) axial forces for five normal walking trials and five medial thrust gait trials. Note different y-axis scales for each gait style.

When the model with new assumptions was applied in blinded fashion to four additional trials of each gait pattern, the predictions resulted in consistently lower rms deviation values than the competition trial predictions. The profiles of the medial and lateral predicted axial forces matched the regressed eTibia data well, although the model had a tendency to underestimate the magnitude of the second force peak during stance (Fig. 4). Over all five normal walking trials, total predicted axial force was different from the eTibia data by an average of 94.2 (SD 99.7) N or 5.61% at the first peak and 368 (SD 30.1) N or 18.41% at the second peak. Over all five medial thrust gait walking trials, total predicted axial force was different from the eTibia data by an average of 453 (SD 541) N or 13.54% for the first peak and 399 (SD 335) N or 17.51% at the second peak.

Discussion

The first aim of the study, to directly compare blinded model predictions to measured in vivo forces for a single trial of normal over-ground gait and a single trial of medial thrust gait, showed that the model compared very well to the in vivo data for both medial and lateral normal forces through the tibial plateau. The medial force predictions were slightly underestimated by the blinded model. Medial thrust gait showed a much greater total force through the implant, particularly in the first half of stance, which was driven by the high external sagittal plane knee moment in the first half of stance. The second aim of the study, to determine strategies that improved our model predictions after unblinding of the in vivo forces, resulted in better medial and lateral force predictions for both gait styles but did not improve predictions of total force through the joint. The third aim of the study, to evaluate all trials of both gait styles after updating the model assumptions to best fit the competition trials, resulted in generally better comparisons between the model and the in vivo forces than the original competition trials.

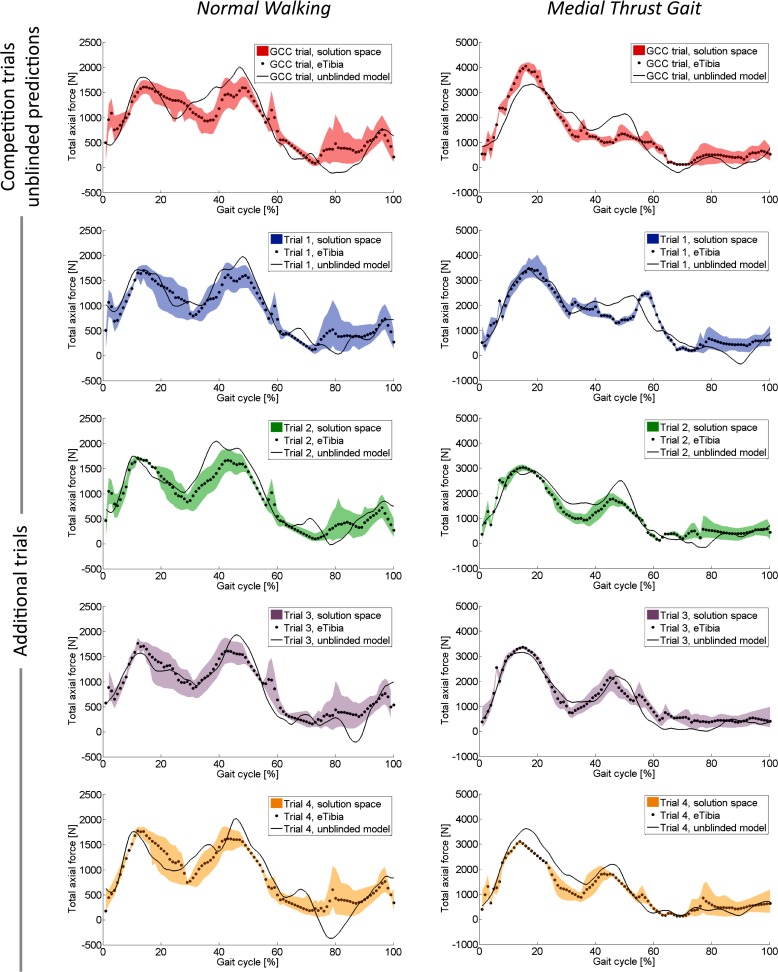
The solution spaces computed by the model allow for the evaluation of variability in contact forces due to internal knee joint structures versus knee joint kinematics and external kinetics. The range of eTibia total forces over all five trials of each gait style was a maximum of 821 N and a minimum of 77 N for normal walking, and a maximum of 1467 N and a minimum of 221 N for medial thrust gait. The envelope of total forces for the solution spaces of forces predicted by the model over all five trials was a maximum of 2186 N and a minimum of 326 N for normal walking and a maximum of 910 N and a minimum of 195 N for medial thrust gait. This suggests that variation in contact forces due to muscle activity was greater than variation in contact forces due to kinematic and kinetic variation for normal walking but not for medial thrust gait. This may be because medial thrust gait is a learned activity and would have more variation in the knee joint kinematics and external kinetics than normal walking, although this was not evaluated in this study.

The strategies for improving model predictions after unblinding of the instrumented TKR forces were not evaluated independently to judge their individual effect on predicted force. In two previous studies we investigated the effect of independently varying (1) single kinematic degrees of freedom, (2) the tibio-femoral contact path, (3) medial-lateral load share, and (4) passive structure contribution [26,27]. While the influence on contact force with regard to variation in tibial rotation and anterior-posterior translation were small (less than 0.1 Body Weight for every ±1 deg or ±1 mm change) the change in maximum contact force was substantial when the tibio-femoral path of contact was varied. Gait-specific tibial translations of the knee were unavailable for this competition. Although the model is relatively insensitive to changes in single degrees of freedom on the order of marker tracking errors, aggregate changes in the patterning and magnitude of multiple joint motions (that would alter the tibio-femoral path of contact) have a larger effect.

Tibio-femoral contact movement has always been perceived as a biomechanically important variable. Anterior-posterior translation directly influences the quadriceps lever arm and, thus, the flexion moment transfer [28]. Femoral rollback helps to increase the mechanical efficiency of the quadriceps muscle but undercuts the effectiveness of the hamstring musculature [17]. Hence, tibio-femoral movement aids in reducing the flexor and extensor forces required for equilibrium. Previous measurements from a cohort of 29 TKR patients demonstrated that tibio-femoral contact movement during gait can be considerable in a TKR device with little constraint [23]. For the competition trials, after unblinding, we used data from a subset of patients with a particularly high anterior-posterior translation of 29.0 mm. This strategy helped to more closely match the medial and lateral peaks not only for normal walking but also for medial thrust gait. It is understood that these motions are implant design specific [29] and dependent on activity and/or gait style [30]. Ideally, these quantities would have been available, either from biplanar fluoroscopy [31] or from marker techniques that allow soft tissue deformation correction [32].

Another limitation was that the generic musculoskeletal model used in OpenSim is based on a male subject while the patient was female. However, an earlier study evaluating the effect of anatomical variation on TKR contact forces suggested only a moderate effect on outcome (typically < 5% variation in force maximum) [27]. Also, we did not utilize the available electromyography (EMC) signals as input to the model. EMG templates could be helpful to reduce the range of the solution space and improve our assumption of up to 5% muscle activation for the antagonist muscle group. This would have been particularly important for the swing phase where the model relied entirely on inertial properties of the body segments. Currently, we are working on strategies to derive indices from EMG to help define antagonistic muscle activity [33]. This may result in improved contact force estimates in the future.

With our model, medial-lateral force predictions are limited by the assumption of the relationship between the forces of the medial and lateral tibial plateaus and the external frontal plane knee moment. The original scaling factor of 17.5% was chosen to result in medial to total contact force ratios ranging from ∼40% at the beginning and end of stance to ∼65% during midstance, which compares well to reports of the medial-lateral load share in the literature [9] and our previous validation study [17]. Since Halder et al. published medial-lateral load sharing up to 90% in their patient population [34], after unblinding, we used linear regression of the single limb stance portion of the frontal plane moment and to compute different scaling factors. This resulted in medial-lateral load share that compared well to the regressions of medial and lateral instrumented forces. Currently, there is uncertainty about the exact correlation between medial-lateral force ratio and adduction moment. Halder et al. [34] recently documented a linear correlation with limb alignment for five subjects with a telemetric knee device. Hence, our use of a linear correlation between the load share and external knee frontal plane moment seems to make sense, as suggested by applying rigorous mechanics.

Contact force predictions improved after changing the passive structure contribution to force and moment equilibrium. In the blinded case, passive structures contributed to the transverse moment balance through a force couple. A force couple could be representative of the resistance to internal-external knee rotation provided by the intraarticular eminence of the tibial plateau. The pattern and magnitude of passive structure contribution (∼10 Nm) compared well to axial torque measured in instrumented total knees [26,35]. In the unblinded case, the additional passive contributions to the frontal plane moment and forces could be representative of constraint provided by the medial or lateral collateral ligaments. In the future, ligaments and other soft tissues can be individually modeled as discrete structures capable of sharing load through the knee.

Finally, yet importantly, this study was limited by the choice of data reporting. Our model calculates a solution space or envelope of contact forces during the gait cycle—not a single solution—and, thus, represents multiple strategies of muscle activation that a person could use during gait. For this study, we compared the eTibia data to the mean force solution at each instance of the gait cycle (which is not necessarily the most likely force solution). When comparing the entire range of contact forces, the solution space overlaps the medial and lateral eTibia forces during the majority of the gait cycle, adding confidence to our model (Fig. 5). Although the mean of the solution space compared well to the eTibia data, additional information should be used in the future to further constrain (i.e., limit possible muscle contributions with EMG data) or expand the solution space in narrow areas (i.e., allow passive structures a reasonable load share).

Fig. 5.

Unblinded model mean predictions (dots) and solution spaces (shaded area) of total axial force compared to the total axial force from eTibia data (line) for five normal walking trials and five medial thrust gait trials. Note different y-axis limits for each gait style.

Conclusions

In this study we directly compared predictions from a mathematical knee model to measured in vivo forces for a single motion trial of normal over-ground gait and a single trial of medial thrust gait. We found that:

• (1)When blinded, we were able to reasonably forecast medial and lateral tibio-femoral contact forces with rms deviation values over 100 points of the entire gait cycle ranging from 234 to 332. Predicted solution spaces of total forces overlapped the instrumented total force patterns, and force maxima were within 15% of instrumented total forces for both gait styles. Specifically, model predictions would have lead to advising the patient against the use of medial thrust gait to lower her medial contact forces.
• (2)After unblinding, the medial and lateral force predictions could be improved by implementation of published knee kinematics typical for cruciate retaining TKR. We, therefore, conclude that knowledge of the trial specific contact kinematics would have increased our model accuracy.
• (3)Applying the improved model to additional trials not part of the competition yielded average rms deviation values of 180 for normal and 233 for medial thrust gait.

In aggregate we, therefore, believe that knowledge of the anterior-posterior knee translation is critical for obtaining accurate force predictions for mathematical knee models following a similar approach as described herein.