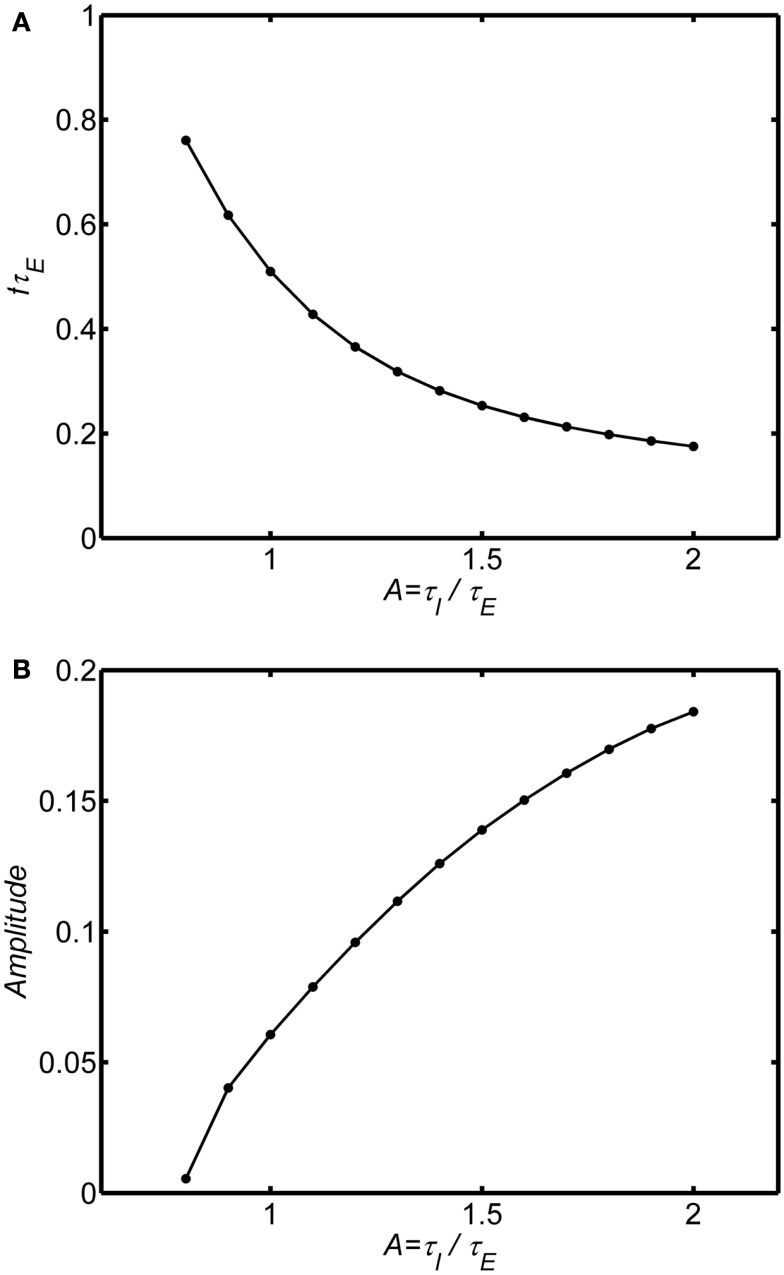
Figure 5.

Effect of the ratio of inhibitory to excitatory time constants in the limit cycle regime. The background state is fixed as E₀(t) = I₀(t) = 0.25. Input is a step function of magnitude P(t) = 0.1. System connection weights are fixed as (w_EI, w_IE, w_II) = (50,15,0) and w_EE = 18 to fix the system in the limit cycle regime. Frequency and amplitude estimated using a Hilbert Transform of the period from of 100τ_E to 200τ_E. Normalized frequency is fτ_E. If τ_E = 10 ms, normalized frequency of 1 is 100 Hz. For A smaller than the range shown for each plot the limit cycle transitions to a damped oscillation. The main result is that increasing τ_E relative to τ_I reduces damping (increasing amplitude) and lowers the frequency of the oscillation. (A) Normalized frequency (B) Amplitude.