INCREASED VOLUNTARY DRIVE IS ASSOCIATED WITH CHANGES IN COMMON OSCILLATIONS FROM 13 TO 60 HZ OF INTERFERENCE BUT NOT RECTIFIED ELECTROMYOGRAPHY

Abstract

The purpose of this study was to compare the capability of interference and rectified electromyography (EMG) to detect changes in the beta (13–30-HZ) and Piper (30–60-HZ) bands when voluntary force is increased. Twenty adults exerted a constant force abduction of the index finger at 15% and 50% of maximum. The common oscillations at various frequency bands (0–500 HZ) were estimated from the first dorsal interosseous muscle using cross wavelets of interference and rectified EMG. For the interference EMG signals, normalized power significantly (P < 0.01) increased with force in the beta (9.0 ± 0.9 vs. 15.5 ± 2.1%) and Piper (13.6 ± 0.9 vs. 21 ± 1.7%) bands. For rectified EMG signals, however, the beta and Piper bands remained unchanged (P > 0.4). Although rectified EMG is used in many clinical studies to identify changes in the oscillatory drive to the muscle, our findings suggest that only interference EMG can accurately capture the increase in oscillatory drive from 13 to 60 HZ with voluntary force.

During voluntary contractions, cortical drive to the motor neuron pool has been typically evaluated with coherent activation between signals recorded from the brain [electroencephalogram (EEG) or magnetoencephalogram (MEG)] and surface-recorded signals from contralateral muscles [electromyogram (EMG)]. MEG–EMG and EEG–EMG coherence has been used to demonstrate common oscillations between the motor cortex and muscle primarily at two frequency bands, known as the “beta” (15–30 HZ) and “Piper” (30–60 HZ; also known as the low-gamma band) bands.¹ These bands are of interest because there is evidence that reflects the communication between higher centers (cortex) and the periphery (muscle)^1,2 and because corticomuscular coherence in these bands differs between neurological patients and healthy adults.^3–7 Recently, some studies have used coherent activation between EMG signals as an indicator of the oscillatory drive to the motor neuron pool from higher centers (EMG–EMG coherence).^3,5,8–11 Interestingly, EMG–EMG coherence appears to provide similar results for EEG–EMG coherence,^3,6,11 which means the two methods can be used interchangeably. Because the EMG–EMG coherence approach is easier to record, it will simplify the identification of the cortical drive to the motor neuron pool for movement-related research and clinical diagnosis.³

Rectification of surface EMG signals is a common processing step used prior to performing EEG–EMG coherence and EMG–EMG coherence.^3,4,10–17 The experimental evidence for rectifying the EMG signal is limited to two studies in the literature.^17,18 Specifically, Myers et al.,¹⁷ using simulations, provided evidence that rectification of the EMG signal can capture the mean discharge rate of motor units, whereas Yao et al.¹⁸ demonstrated that EEG–EMG coherence was similar when either interference EMG or rectified EMG signals were used. Recent evidence from our laboratory, however, questions the use of EMG rectification for EMG–EMG coherence.¹⁹ The findings of that study were based on manipulating EMG signals that were reconstructed from experimentally recorded EMG signals. Rectification of the EMG signal significantly impaired the accuracy of estimating the original input to the signal and the common oscillations between two EMG signals. In contrast, when the interference EMG signal was used, the known input to an EMG signal and the known common input between two EMG signals were accurately captured.

Previous findings^1,20 suggest that the strength of corticomuscular coherence in the beta band and Piper band changes differently with the level of voluntary force exerted. Specifically, the beta band decreases, and the Piper band increases with the level of voluntary force.^1,20 Although these findings occurred with the use of rectified EMG, the changes at the muscle level should be similar with both interference and rectified EMG, because MEG–EMG coherence and EEG–EMG coherence are similar regardless of whether the EMG signal is rectified or not.¹⁸ The purpose of this experiment, therefore, was to compare the sensitivity of the interference and rectified EMG wavelet spectrum to detect changes in the strength of the beta and Piper bands when voluntary force increases from 15% to 50% MVC. Based on findings from our previous study,¹⁹ we hypothesized that the interference but not the rectified EMG would be sensitive to changes in the beta and Piper bands in muscle activity with an increased voluntary force level. A portion of the experimental recordings have been reported in a previous study.²¹

METHODS

Subjects

Twenty young adults (20–32 years of age, 10 men and 10 women) volunteered to participate in our experiment. All subjects reported being healthy without any known neurological problems, were right-handed according to a standardized survey,²² and had normal or corrected vision. The institutional review board at Texas A&M University approved the procedures, and subjects provided written informed consent before participation in the investigation. This study was performed in accordance with the ethical standards of the 1964 Declaration of Helsinki.

Task

Subjects were instructed to accurately match the target force at 15% and 50% (three trials each) of their maximal isometric force with abduction of the index finger. Visual feedback was given with a gain equal to 12.8 pixels/N (visual angle was ~0.3°). Subjects were instructed to gradually push against a force transducer and increase the force applied to match the target force within 3 s. When the target was reached, subjects were instructed to maintain their force on the target as accurately and as consistently as possible. Each trial lasted 22 s, and visual feedback was removed at 8–12 s and at 16–20 s. To avoid possible influences of visual corrections in the EMG power spectra, only data obtained without visual feedback were analyzed in this study. The two time periods were analyzed as separate trials and then averaged.

EMG Recordings

First dorsal interosseous (FDI) muscle activity was recorded with two pairs of gold disk electrodes (4 mm; Model F-E6GH; Grass Technologies, West Warwick, Rhode Island) taped on the skin, relative to the innervation zone, which is located approximately at about one third of the muscle length.²³ One electrode from the first pair was placed around the innervation zone and the other proximal to the innervation zone. Both electrodes of the second pair were placed distal to the innervation zone, and the second electrode was placed close to the insertion of the FDI muscle. The center-to-center distance between the two electrodes was 5 mm. The reference electrode was placed over the ulnar styloid. The EMG signal was amplified (× 2000) and bandpass filtered at 3–500 HZ. Data were acquired using Spike 2 (version 6.02) software (Cambridge Electronic Design, Cambridge, UK) and analyzed off-line using custom-written programs in MATLAB (The Math-Works, Inc., Natick, Massachusetts).

Common Oscillations Quantification

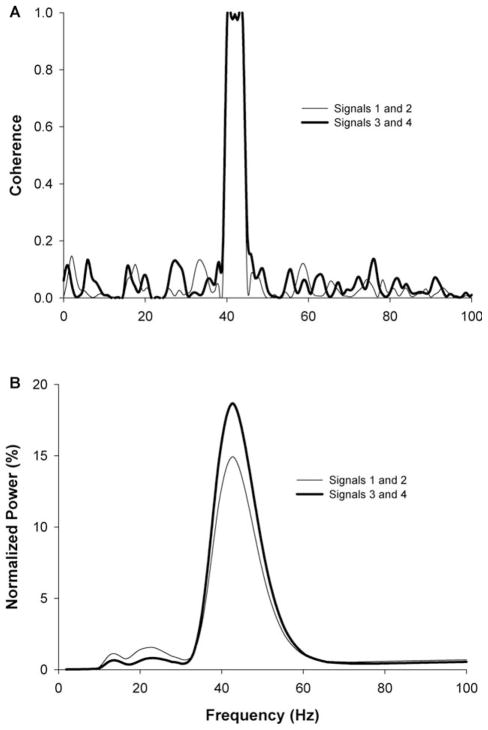
To determine the common oscillations between pairs of EMG signals, normalized cross-wavelet spectra of both the interference and rectified EMG signals were used instead of coherence. This was done because coherence does not take into account the relative strength of common frequencies from the contributing signals, as demonstrated in Figure 1 with two pairs of simulated signals. Each pair had a common frequency at 42 HZ, but different amplitudes in that frequency. It is clear that, although both the coherence and normalized cross-wavelet spectrum identify the same common frequency between the two signals, only the cross-wavelet spectrum is sensitive in identifying the amplitude differences between the two pairs. The normalized cross-wavelet spectrum, therefore, is as sensitive as coherence in identifying the common frequencies in two signals. In addition, it provides important information about the relative amplitudes of the common frequencies in the original signals, which coherence cannot do. Finally, wavelet analysis provides other significant advantages to Fourier transformation, which have been outlined elsewhere.²⁴ Thus, this technique allows for comparison of the relative strength of common oscillations across different frequency bands and across different conditions.

FIGURE 1.

Coherence and normalized cross-wavelet power spectra for two pairs of 10-s simulated signals with 3 dB of noise. The first pair of signals (thin line) were (numbers in parentheses represent the amplitude of each frequency): signal 1—23 (5) HZ and 42 (5) HZ for the first half of the signal (0–5 s) and 13 (5) HZ and 42 (5) HZ for the second half (5–10 s); signal 2—13 (5) HZ and 42 (5) HZ for the first half of the signal and 23 (5) HZ and 42 (5) HZ for the second half. The second pair of signals (thick line) were: signal 3—23 (5) HZ and 42 (20) HZ for the first half of the signal and 13 (5) HZ and 42 (20) HZ for the second half; signal 4—13 (5) HZ and 42 (20) HZ for the first half of the signal and 23 (5) HZ and 42 (20) HZ in the second half. This figure demonstrates that the normalized cross-wavelet can identify the common frequencies between two signals equally well to coherence and it provides information regarding the amplitude of the common frequencies that the coherence does not.

Cross-Wavelet Spectra

To obtain the cross-wavelet spectra for a pair of EMG signals, first the continuous wavelet transforms of each EMG signal were calculated separately. The wavelet transform of an EMG signal determines both the amplitude-versus-frequency characteristics of the signal and how this amplitude varies with time. The wavelet represents a set of functions with the form of small waves created by dilations and translations from a simple generator function, Ψ(t), which is called the mother wavelet.²⁵ To perform a wavelet transform several different generator functions can be used. In this investigation, as in most studies that have used wavelet transforms to quantify the frequency content of EMG signals,^26–29 the Morlet mother wavelet was used³⁰:

$${\mathrm{\Psi }}_0(t)={\pi }^{-\frac{1}{4}}{e}^{i{\omega }_0\eta }{e}^{\frac{-{\eta }^2}{2}}$$ (1)

where η is dimensionless time and w₀ is dimensionless frequency (in this study we used w₀ = 6, as suggested by Grinsted and colleagues³¹).

The Morlet wavelet (with w₀ = 6) is appropriate when performing wavelets and cross-wavelet analyses, because it provides a reasonable balance between time and frequency localization.³¹ The wavelet transform applies the wavelet function as a bandpass filter to the time-series eq. (2). To modify its frequency content, the wavelet function is stretched in time by varying its scale (s) (dilation). For the Morlet wavelet used in this study the wavelet scale is almost equal to the Fourier period (Fourier period = 1.03 s):

$$W{(s,\tau )}^X=\int X(t){\mathrm{\Psi }}_{s,\tau }^{\ast }(t)dt$$ (2)

where s represents the dilation parameter (scale shifting), τ represents the location parameter (time shifting), and the basic function Ψ_sτ(t) is obtained by dilating and translating the mother wavelet Ψ₀(t).²⁵

Morlet wavelet transforms were obtained using a base algorithm, developed by Torrence and Compo³⁰ (available at: http://paos.colorado.edu/research/wavelets). From the wavelet transform of both signals, the cross-wavelet transform was calculated:

$$W{(s,\tau )}^{XY}=W{(s,\tau )}^{X}W{(s,\tau )}^{Y\ast }$$ (3)

where W(s,τ)^XY is the cross-wavelet transform of signals X(t) and Y(t), W(s,τ)^X is the wavelet transform of signal X(t), and W(s,τ)^Y* is the complex conjugate of the wavelet transform of signal Y(t). The cross-wavelet power spectrum (XWPS) is defined as the modulus of the cross-wavelet transform, eq. (4)³⁰; it exposes regions with high common power between the two signals³¹:

$$\mathit{XWPS}{(s,\tau )}^{XY}=\mid W^{XY}(s,\tau )\mid$$ (4)

We defined the normalized cross-wavelet scale-averaged power spectrum (NXWPS; Fig. 2) as the weighted modulus of the cross-wavelet transform normalized by the weighted average of the cross-wavelet power spectrum over all scales:

$$\mathit{NXWPS}{(s,\tau )}^{XY}=\frac{\mid W^{XY}(s,\tau )\mid /s}{{\sum }_s{\sum }_t\left(\frac{\mid W^{XY}(s,\tau )\mid }{s}\right)/n}\times 100(\%)$$ (5)

where n is the number of samples in signals X(t) and Y(t). The normalized cross-wavelet scale-averaged power spectrum (hereafter referred to as the normalized cross spectrum) shows the relative importance of each frequency of the wavelet power spectrum. It considers the relative importance of the commonalities in the variance of the two signals in different frequencies through time. Thus, the normalized cross spectrum can be used to compare the strength through time of common oscillations within the same pair of EMG signals and among different pairs of EMG signals.

FIGURE 2.

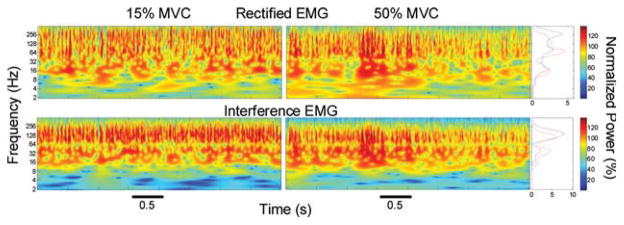
Examples of normalized cross-wavelet power spectra (image plot, four graphs at the center of the figure) and mean normalized cross-wavelet power spectra (line plots, two graphs at the right side of the figure). Cross-wavelet spectra were obtained from rectified (top row) and interference (bottom row) EMG signals from the same subject, while performing contractions at 15% (left column; blue lines) and 50% (right column; red lines) of the MVC. The interference cross-wavelet spectra and mean cross-wavelet spectra showed an increase in normalized power around 16–64 HZ and a decrease around 64–256 HZ when comparing the higher force level with the lower force level. In contrast, the rectified cross-wavelet spectra and mean cross-wavelet spectra showed no significant changes at 16–64 HZ, an increase in normalized power around 64–128 HZ, and a decrease around 128–500 HZ, when comparing 50% MVC force level with 15% MVC force level. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Using the normalized cross-wavelet spectrum, we quantified the normalized power and normalized power per HZ from seven different frequency bands (5–13, 13–30, 30–60, 60–100, 100–150, 150–200, 200–500 HZ). Normalized power of a certain frequency band was defined as the total power averaged in time within the band. Normalized power per HZ of a certain frequency band was defined as the normalized power of the band divided by its frequency range (e.g., divided by 30 HZ for the 30–60-HZ frequency band).

Cross-Talk and Common Input

Given the small size of the FDI and the proximity of the electrodes to one another, it is possible that common oscillations estimated by the cross-wavelet are caused by cross-talk. Although previous studies have used other techniques to identify cross-talk,³² we performed the following to determine whether potential differences in the normalized power within the beta and Piper bands from low to high forces could be entirely explained by cross-talk: (1) quantification of the ratio of the normalized wavelet spectrum between the first (EMG1) and second (EMG2) pair of electrodes (EMG1:EMG2); and (2) comparison of EMG1:EMG2 across five frequency bands that were within the beta and Piper bands (12–20, 20–28, 28–36, 36–44, 44–52 HZ) and across force levels. If the ratio was similar across frequencies in both force levels, then changes within the bands of interest could have been entirely explained by cross-talk. However, if the ratio changed differently across frequencies and force levels, it would imply that EMG1 and EMG2 were different from each other within the bands of interest, and thus cross-talk would not entirely explain the common oscillations.

Statistical Analyses

A three-way analysis of variance (ANOVA; 2 EMG methods × 2 force levels × 7 frequency bands) with repeated measures on all factors was used to compare the normalized power and the normalized power per HZ of the cross-wavelet power spectra of the interference EMG and rectified EMG signals across the two different force levels. In addition, a two-way ANOVA (2 force levels × 5 frequency bands) with repeated measures on all factors was used to compare the EMG1:EMG2 across frequency bands and force levels. Analyses were performed with SPSS (version 16.0) statistical software (SPSS, Inc., Chicago, Illinois). Significant interactions from the ANOVA models were followed by appropriate post hoc analyses. For example, differences among conditions and frequencies were followed with paired t-tests and one-way ANOVAs. Multiple t-test comparisons were corrected using the Bonferroni correction. The alpha level for all statistical tests was 0.05. Data are reported as mean ± SD in the text and as mean ± standard error of the mean (SEM) in the figures. Only the significant main effects and interactions are presented, unless otherwise noted.

RESULTS

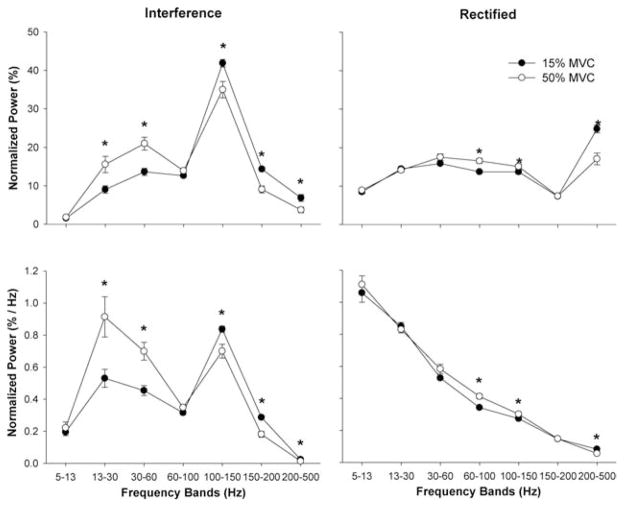
The cross-wavelet power spectra of the interference and rectified EMG signals (Fig. 2) were different. Specifically, there was a significant EMG method × force level × frequency band interaction for the normalized power (F_6,114 = 11.4, P < 0.001) and normalized power per HZ (F_6,114 = 8.6, P < 0.001). Post hoc analyses indicated that, at 15% of MVC, the normalized power and normalized power per HZ were significantly different (P < 0.001) between the interference and rectified EMG signals for the 5–13-, 13–30-, 100–150-, 150–200-, and 200–500-HZ frequency bands. At 50% of MVC, post hoc analyses indicated that the normalized power and normalized power per HZ were significantly different (P < 0.001) between the interference and rectified EMG signals for the 5–13-, 100–150-, and 200–500-HZ frequency bands.

The change in common EMG oscillations with voluntary force using the interference and rectified EMG method is shown in Figure 3. When the interference EMG method was used, both the normalized power and normalized power per HZ from the cross-wavelet spectra increased significantly (P < 0.001) in the beta (13–30 HZ) and Piper (30–60 HZ) bands with the increase in voluntary force (Fig. 3, left column). The power from 100 to 150 HZ decreased significantly (P < 0.001), whereas other bands were unaffected by the force change. In contrast, when the rectified EMG method was used, both the normalized power and normalized power per HZ from the cross-wavelet spectra did not change significantly (P > 0.4) in the beta and Piper bands with voluntary force (Fig. 3, right column). Normalized power in the cross-wavelet of the rectified EMG signals changed significantly (P < 0.001) from 60 to 100 HZ (increased) and 200 to 500 HZ (decreased) with force.

FIGURE 3.

The overall results for normalized power and normalized power per HZ for the interference (left column) and rectified (right column) EMG signals obtained while subjects performed contractions at 15% and 50% of their MVC. For both the normalized power and normalized power per HZ, the interference EMG signals exhibited greater power (P < 0.001) in the 13–30-HZ and 30–60-HZ frequency bands and lower power between 100 and 500 HZ (left column) at 50% compared with 15% MVC. In contrast, rectified EMG signals exhibited greater power between 60 and 150 HZ and lower power between 200 and 500 HZ (right column) at the higher force level. Asterisk indicates significant differences between the two force levels.

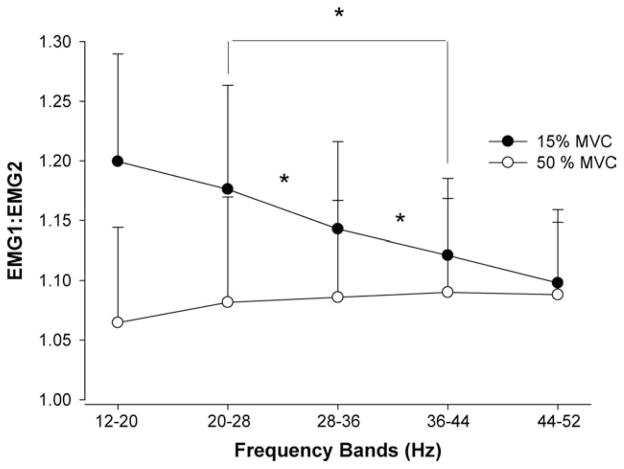
To determine whether the significant increase in the beta band and Piper band with force was entirely caused by cross-talk between the two pairs of electrodes, we quantified the changes in EMG1:EMG2 within 12–52 HZ at the two force levels (Fig. 4). There was a significant force level × frequency band interaction (F_4,76 = 3.026, P = 0.023). Post hoc analyses indicated that, at 15% MVC, EMG1:EMG2 progressively decreased from 20–28 HZ to 36–44 HZ, whereas, at 50% MVC, the power did not change significantly across frequencies. On average, EMG1:EMG2 was greater for the lower force compared with the upper force level. Subsequent analysis showed that the greater ratio in the lower force level occurred because EMG1 was greater than EMG2, whereas, during the higher force level, EMG1 and EMG2 were similar (EMG2 increased). Therefore, these results suggest that changes in normalized cross-wavelet power within those frequency bands across force levels cannot be entirely explained by cross-talk.

FIGURE 4.

The ratio of the normalized power (EMG1:EMG2) recorded from the first pair of electrodes (EMG1) and second pair of electrodes (EMG2) placed on the first dorsal interosseous muscle from 12 to 52 HZ and force levels. There was a significant force × frequency interaction, which indicated the following: (1) at 15% of MVC, the ratio was significantly higher for frequency bands at 20–28 HZ compared with 28–36 HZ and 36–44 HZ, and for 28–36 HZ compared with 36–44 HZ; and (2) across all frequency bands, EMG1:EMG2 was greater for the lower force level. Asterisk indicates significant differences between frequency bands.

DISCUSSION

Previous studies have used rectified EMG signals to identify oscillatory drives in muscle activity.^{3–5,11–18} However, based on recent EMG simulations,¹⁹ there is evidence that the rectified EMG signal does not accurately capture the imposed oscillations in the EMG signal. Only the interference EMG signal reliably captured the imposed oscillations. In this study we sought to determine whether using interference EMG would also be advantageous over the use of rectified EMG signal when the oscillatory drive varied physiologically. To accomplish this we varied the voluntary force from 15% to 50% of maximum. Based on previous corticomuscular coherence findings^1,20 and the proposition that corticomuscular coherence is similar with the use of the interference and rectified EMG,¹⁸ a reasonable expectation is that the strength of the oscillatory drive at the muscle level would decrease from 13 to 30 HZ (beta band) and increase from 30 to 60 HZ (Piper band) with increased voluntary force for both the interference and rectified EMG signals. In contrast, our findings clearly demonstrate that the expected increase in oscillatory drive from 30 to 60 HZ with voluntary force was captured only with the use of interference EMG signals but not with the use of rectified EMG signals. In addition, we found that oscillatory drive to the muscle also increased from 13 to 30 HZ with the interference EMG signal but did not change for the rectified EMG signal. These results, therefore, extend our recent simulation findings to physiological recordings and suggest that interference EMG signals and not rectified EMG signals must be used to accurately capture changes in the oscillatory activation of muscle.

Identifying Oscillatory Changes in Muscle Activity with Interference and Rectified EMG

The finding that the normalized power of the cross-wavelet from 30 to 60 HZ increased with voluntary force supports previous claims that an increase in the voluntary descending input to the motor neuron pool is associated with stronger oscillatory drives at the Piper band (30–60 HZ).^1,20 However, our results clearly demonstrate that to be able to reliably see this increase in oscillatory drive at the Piper band, the interference EMG signal and normalized cross-wavelet spectrum must be used. The rectified EMG was insensitive to changes in voluntary force at the bands of interest. Therefore, this result extends our previous findings,¹⁹ which were based on simulated changes in the oscillatory drive, to physiological variations in the oscillatory drive. Overall, both studies challenge the use of rectified EMG as an accurate way to identify the strength of common oscillatory drives between two EMG signals, especially when the bands of interest are at 13–60 HZ. The inability of the rectified EMG to accurately identify common oscillatory drives may be related to the non-linear transformation of frequencies when the EMG is rectified.^18,19,33

Interestingly, muscle activity oscillations also increased from 13 to 30 HZ with voluntary force. This is contrary to our expectations, which were based on previous findings,²⁰ that the power in the beta band would decrease with voluntary force. The following reasons may explain this discrepancy: (1) The study by Brown et al.²⁰ examined MEG–EMG coherence with force, whereas our study determined the changes in muscle activity oscillations with force. Therefore, it is possible that, although activation of the muscle included greater oscillations from 13 to 30 HZ with force, MEG–EMG coherence decreased because the oscillatory activity of the motor cortex decreased at that frequency band with force. The 13–30-HZ oscillations in muscle, therefore, may come from other sources, including sensory feedback.^34,35 (2) Coherence from 13 to 30 HZ became non-significant (close to 0) at maximal force contractions. At moderate force levels the coherence was still significant and close to that observed at low force levels. In this study, our high force level was 50%, which can be considered moderate. (3) The MEG–EMG coherence in the study by Brown et al.²⁰ was quantified by using rectified EMG signals. The findings clearly demonstrate that rectified EMG did not change significantly at 13–60 HZ with voluntary force. Therefore, their results may be heavily influenced by changes at the cortical level and not necessarily by changes at both the cortical and muscle levels. Future studies should compare corticomuscular coherence at various force levels with the interference EMG signal.

Cross-Talk and Changes in Common Input

For the following reasons we believe that the observed increases in the normalized cross-wavelet from 13 to 60 HZ with force likely represent a stronger common oscillatory drive to the motor neuron pool with force and are not caused only by amplified cross-talk between our electrodes. First, we demonstrated (see Fig. 4) that the two pairs of electrodes were recording significantly different signals. If the two pairs were recording similar signals due to their proximity in a small muscle (cross-talk), then the ratio between them should be constant across frequency bands. However, we found that, at 15% MVC, the ratio changed across frequency bands, which indicates that the two pairs of electrodes were not recording the same signal. Second, we demonstrated that there were significant differences between the signals recorded at 15% and 50% MVC. The ratio was significantly greater for 15% MVC compared with 50% MVC. The greater ratio occurred because the first pair of electrodes exhibited greater normalized wavelet power than the second pair of electrodes at 15% MVC, whereas the two pairs of electrodes exhibited similar normalized wavelet power at 50% MVC due to a selective increase in the normalized wavelet power from the second pair of electrodes (the first one did not change). This finding suggests that additional motor units were selected during the higher force level, and they were likely motor units that had a significant number of fibers closer to the distal part of the first dorsal interosseous muscle (where we placed the second pair of electrodes). Therefore, these findings suggest that cross-talk cannot entirely explain the increased normalized power in the beta and Piper bands with force. Finally, even if the normalized power from 13 to 60 HZ does not represent a clean measurement of common input to the motor neuron pool, our findings do demonstrate that greater voluntary force is associated with increased oscillations in muscle activity from 13 to 60 HZ.

Clinical and Neural Control Implications

These findings have significant clinical and neural control implications. For example, there has been an effort to use the strength of the common frequencies between pairs of surface EMG electrodes (EMG–EMG coherence) as an indicator of corticomuscular coherence.^3–5,7,10 This technique is preferable in the clinic for diagnostics because of its simplicity and ease of use on patients.³ In addition, the present findings have implications for understanding the neural control of movements in healthy adults during different conditions. For example, EMG–EMG coherence was recently used to determine the effect of alcohol on postural control,⁸ the influence of fatigue on hand muscle synergy,³⁶ and the consequence of visuomotor skill training on leg muscle activity.³⁷ Nonetheless, the results from this study, along with our simulated findings,¹⁹ suggest that the conclusions drawn from all of these previous studies may be limited, because they used rectified EMG instead of interference EMG.

In conclusion, our findings demonstrate that greater voluntary force is associated with increased oscillatory muscle activity from 13 to 30 HZ and 30 to 60 HZ. Hence, our data support previous findings²⁰ that demonstrated increased corticomuscular coherence from 30 to 60 HZ with stronger contractions. Most importantly, we found that interference EMG signals and not rectified EMG signals must be used to accurately capture the increase in oscillatory drive at the Piper (30–60-HZ) band with voluntary force, which extends recent findings using simulations¹⁹ to physiological recordings.

Abbreviations

ANOVA

analysis of variance

EEG

electroencephalogram

EMG

electromyography

FDI

first dorsal interosseous

MEG

magnetoencephalogram

MVC

maximum voluntary contraction