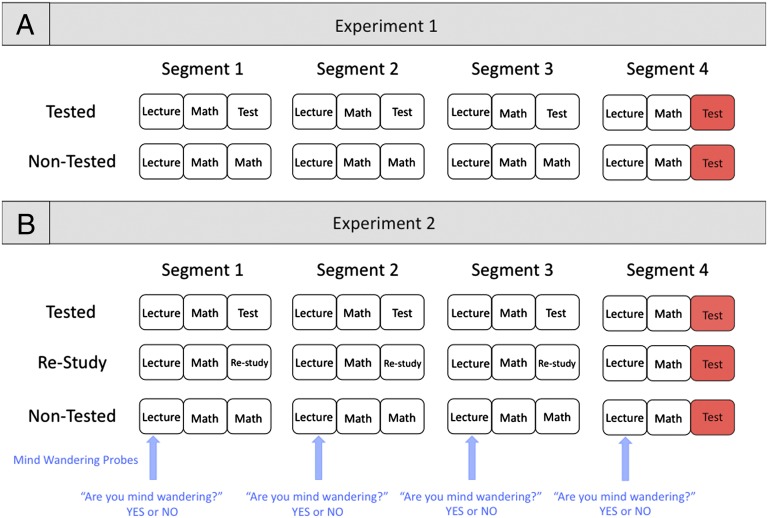
Fig. 1.

Schematic of the design of experiments 1 and 2. (A) In experiment 1, students were instructed that they would learn a 21-min excerpt of a statistics lecture that was divided into four segments (∼5.5 min each). Students were further told that each lecture segment would be followed first by 1 min of arithmetic problems (e.g., 13 × 7; six problems; 10 s per problem), and then either a 2-min quiz about the most recent lecture segment (e.g., “Explain the relation between a population and a sample”; six questions; 20 s per question) or 2 more min of arithmetic (12 problems; 10 s per problem). In fact, there were two testing schedules. One group of students was tested after each lecture segment (tested), whereas another group was only tested after the fourth lecture segment (nontested). To assess the learning of the end of the lecture, we compared the proportion of questions students in the tested and nontested groups correctly answered about the fourth lecture segment. (B) In experiment 2, students were told that each lecture segment, and the arithmetic problems that followed, would be followed by either (i) a 2-min quiz about the most recent lecture segment (tested group; six questions; 20 s per question), (ii) a restudy phase during which participants would be presented with answers to key questions about the most recent lecture segment (restudy group; six question–answer pairs; 20 s per question–answer pair; same questions as tested group), or (iii) more arithmetic problems (nontested group; 12 problems; 10 s per problem). To assess learning of the end of the lecture, we compared the proportion of questions students in the tested, restudy, and nontested groups correctly answered about the fourth lecture segment. Additionally, students in experiment 2 were asked to indicate whether their minds had wandered away from the content of the lecture at four random intervals during the lecture (once per lecture segment).