Computational Investigation of the pH Dependence of Loop Flexibility and Catalytic Function in Glycoside Hydrolases

Background: Solution pH affects cellulase enzyme activity.

Results: We used simulation to predict pH-dependent behavior in cellulases, including pK_a values for the catalytic machinery, ring distortion, and loop flexibility.

Conclusion: pH increases active site tunnel flexibility and affects the −1 carbohydrate ring distortion, suggesting pH-dependent mechanisms for complexation and catalysis of cellulose chains.

Significance: These results provide molecular-level understanding of pH effects on cellulases.

Abstract

Cellulase enzymes cleave glycosidic bonds in cellulose to produce cellobiose via either retaining or inverting hydrolysis mechanisms, which are significantly pH-dependent. Many fungal cellulases function optimally at pH ∼5, and their activities decrease dramatically at higher or lower pH. To understand the molecular-level implications of pH in cellulase structure, we use a hybrid, solvent-based, constant pH molecular dynamics method combined with pH-based replica exchange to determine the pK_a values of titratable residues of a glycoside hydrolase (GH) family 6 cellobiohydrolase (Cel6A) and a GH family 7 cellobiohydrolase (Cel7A) from the fungus Hypocrea jecorina. For both enzymes, we demonstrate that a bound substrate significantly affects the pK_a values of the acid residues at the catalytic center. The calculated pK_a values of catalytic residues confirm their proposed roles from structural studies and are consistent with the experimentally measured apparent pK_a values. Additionally, GHs are known to impart a strained pucker conformation in carbohydrate substrates in active sites for catalysis, and results from free energy calculations combined with constant pH molecular dynamics suggest that the correct ring pucker is stable near the optimal pH for both Cel6A and Cel7A. Much longer molecular dynamics simulations of Cel6A and Cel7A with fixed protonation states based on the calculated pK_a values suggest that pH affects the flexibility of tunnel loops, which likely affects processivity and substrate complexation. Taken together, this work demonstrates several molecular-level effects of pH on GH enzymes important for cellulose turnover in the biosphere and relevant to biomass conversion processes.

Introduction

Plant biomass is the most abundant and renewable resource for conversion to sustainable fuels and chemicals in the near term (1, 2). In nature, organisms secrete multifunctional cellulase enzyme mixtures, consisting of endoglucanases, cellobiohydrolases, β-d-glucosidases, and lytic polysaccharide monooxygenases (3–5), which work synergistically to degrade cellulose in plant cell walls, and these natural mixtures provide an excellent starting point for the development of enzymatic catalysts to convert plant cell walls to monomeric sugars for the production of renewable fuels (6). Cellulase enzymes comprise many glycoside hydrolase (GH)³ families (7); among them, cellobiohydrolases from GH family 6 (GH6) and GH family 7 (GH7) are often found as the two most abundant enzymes in native fungal secretomes, as observed in the well characterized model ascomycete fungus Hypocrea jecorina (Trichoderma reesei) (8, 9). In particular, H. jecorina Cel6A hydrolyzes cellulose chains from the nonreducing end via an inverting mechanism to produce α-cellobiose, whereas H. jecorina Cel7A cleaves β-cellobiose from the reducing end via a retaining mechanism (10–15).

Solution pH is a critical experimental parameter that has long been known to affect the activity of cellulase enzymes. Many experimental studies have been conducted to understand and modify the pH-dependent activities of cellulase enzymes (16–21). H. jecorina Cel6A and Cel7A function optimally at pH ∼5 on cellotetraose (Cel6A) (22), 3,4-dinitrophenyl lactoside (Cel7A) (16), and 4-nitrophenyl α-d-glucopyranoside (Cel7A) (23), and their activities decrease dramatically at other pH values. Experimental studies using directed evolution have revealed that certain mutants of H. jecorina Cel7A and Cel5A have higher pH optima compare with the wild type (16, 19). Carboxyl-carboxylate pair mutations have been used to stabilize H. jecorina Cel6A at neutral or alkaline pH (21). Additionally, Cockburn et al. (24, 25) demonstrated that replacing the general base residue Asp-392 with cysteine sulfinate and removing the surface-charged residues in Cellulomonas fimi GH6 endoglucanase cellulase A (CenA) induced both a broadening and an acidic shift in the pH profile of CenA. Understanding the pH optimum shifts in these mutant cellulases at the molecular level is essential to design new cellulase mutants to function optimally at the desired pH values.

Recently, Pingali et al. (26) used small angle neutron scattering to examine the solution structures of Cel7A at different pH values, and their results suggest that the Cel7A catalytic domain (CD) becomes more flexible near the optimal pH for enzyme activity. They speculated that increased flexibility has the potential to enhance substrate access to the active site, thus increasing the enzyme activity. This study provides important insights into the pH dependence of the structure of the Cel7A CD. However, these experiments were not able to identify the flexible regions in the CD at the molecular level, which can be elucidated by computational studies.

Molecular dynamics (MD) simulation can provide a molecular-level understanding of cellulase action as a complement to experimental studies (2, 27). Several computational studies have used MD to identify new functions of cellulase subdomains (28–31) and to characterize the binding affinity of cello-oligomer ligands for wild-type and mutant cellulases (32–34). Most previous computational studies of cellulases have been conducted under the conventional MD schemes, wherein the protonation state of ionizable residues (aspartic acid, glutamic acid, and histidine) is fixed based on their pK_a values. This assumption of static protonation is problematic for certain questions of interest because the pK_a of an ionizable residue is typically unknown in its protein environment, whereas the protonation/deprotonation process is coupled to the dynamics of the protein local environment. Neglecting the dynamics of the ionization equilibrium can potentially preclude detailed understanding of pH-coupled biological phenomena. To accommodate the protonation/deprotonation process of a titratable residue, the constant pH molecular dynamics (CPHMD) method was developed to directly couple solution pH conditions to the protonation states of protein ionizable residues, which can fluctuate in response to solution pH and the protein local conformational state (35, 36).

Here, we used a novel, hybrid, solvent-based CPHMD method combined with pH-based replica exchange (pH-REX) (37) to investigate the pH optima of H. jecorina Cel6A and Cel7A with and without a substrate bound in the CD. The hybrid solvent model utilizes the efficiency of the generalized Born implicit solvent model (38) for calculating the solvation force acting on the titration coordinates, whereas the protein conformation is still driven by the more accurate explicit solvent model (37). The pH-REX method enables exchange between replicas simulated at different solution pH values, thus enhancing the sampling of protein conformational space and protonation state of titratable residues (39). Additionally, as GH activity depends on strained, non-chair conformations at the −1 ligand-binding sites (40), we investigated how solution pH can affect the conformation of glucose at the −1 position of both enzymes. Finally, we examined the overall structures of the Cel6A and Cel7A CDs at different solution pH values, particularly the flexibility of the tunnel-forming loops, to compare with the experimental small angle neutron scattering study (26). Our results elucidate several molecular-level aspects of how pH affects cellulase action.

EXPERIMENTAL PROCEDURES

Structure Preparation

The atomistic models of the CDs of Cel6A and Cel7A were constructed using the reported crystal structure (Protein Data Bank code 1QK2) (41) and the theoretical model (code 8CEL) (14), respectively. The substrate-bound systems, referred to hereafter as “bound” systems, consisted of a cellohexaose oligomer in the active site of Cel6A and a cellononaose oligomer bound in the active site of Cel7A. Systems referred to as “free” hereafter contained the enzyme excluding the cellodextrin. Glycosylation of cellulases was not considered in this work.

All simulations were conducted using CHARMM (42). The CHARMM22 force field parameters (42, 43) with the CMAP correction (44–46) were used for the enzymes, and the C35 carbohydrate force field parameters (47, 48) were used for the cellodextrin substrates. The proteins were placed in an equilibrated truncated octahedral box of TIP3P water molecules (49, 50). Ions were added into the system to maintain charge neutrality. The systems were equilibrated in the NPT ensemble at 300 K using a Nosé-Hover thermostat (51, 52) and 1 atm for 100 ps with a step size of 1 fs. SHAKE was used to fix the covalent bonds to hydrogen atoms (53). The non-bonded interactions were truncated with a 10 Å cutoff. The electrostatic interactions were calculated using the particle mesh Ewald method (54) with a sixth-order b-spline interpolation, a Gaussian distribution width of 0.34 Å, and a mesh size of 96 × 96 × 96 for Cel7A and 72 × 72 × 72 for Cel6A. The final system size was ∼56,000 atoms for Cel7A and 36,000 atoms for Cel6A.

CPHMD

The CPHMD method is based on the λ-dynamics approach to free energy calculations (55), allowing the titratable protein residues to switch continuously between protonated and deprotonated states. An alchemical titration coordinate, λ, is introduced for each titratable protein residue to accommodate protonation and deprotonation. More details of the CPHMD method can be found elsewhere (35, 56). There are a total of 33 titratable residue (20 aspartic acid, 9 glutamate, and 4 histidine residues) in Cel6A and 47 titratable residues (24 aspartic acid, 19 glutamate, and 4 histidine residues) in Cel7A. All of the titratable residues were subjected to ionization in the CPHMD simulations. The CPHMD simulations were conducted using the PHMD facility in CHARMM (42). The solvation forces on the titration coordinates were calculated using the generalized Born with simple switching implicit solvent model (57) with the refined atomic input radii of Nina et al. (58, 59). All simulations were performed in the NPT ensemble at 300 K and 1 atm using the same parameters as the equilibrium simulations with a step size of 2 fs.

pH-REX

pH-REX MD simulations were conducted for both free and bound enzymes. Twelve pH replicas using the same CPHMD conditions and parameters as described above were used in the pH-REX simulations of Cel6A, ranging from pH 2.0 to 7.5, with a spacing of 0.5 pH units. Eighteen pH replicas were used in Cel7A, ranging from pH 1.0 to 7.8, with a spacing of 0.4 pH units to ensure an acceptance ratio of 40%. The exchange in pH was attempted every 500 dynamics steps or 1 ps. Each replica was simulated for 8 ns in the NPT ensemble.

Calculation of pK_a Values

The populations of protonated and deprotonated states from simulations of different pH replicas were recorded. The pK_a values of titratable residues in protein can be computed by fitting the deprotonated fractions (S) to the generalized Henderson-Hasselbach equation (60): S = 1/(1 + 10^n(pKa−pH)), where n is the Hill coefficient, which represents the slope of the transition region of the titration curve. The statistical uncertainty was estimated as half of the difference between the pK_a values calculated from the first and second halves of the 8-ns CPHMD simulation.

Potential of Mean Force (PMF) for Ring Pucker

We used umbrella sampling (61) to construct the free energy profiles associated with the conformational change in the glucose ring from a chair conformation to a skew conformation at the −1 site at different solution pH values. Umbrella sampling simulations were conducted at pH 2, 5, and 7. For each pH case, the reaction coordinate is the Cremer-Pople ring pucker amplitude (62) of the glucose residue at the −1 site. The ²S₀ conformation at the −1 site in Cel6A is defined by an amplitude of 0.73 Å, and the chair conformation is defined by an amplitude of 0.57 Å (63). The possible ¹S₃ and ^1,4B conformations at the −1 site in Cel7A are both located at the equator in the Cremer-Pople coordinates and thus have the same pucker amplitude as ²S₀. Therefore, the Cremer-Pople ring pucker amplitude was sampled in 12 separate umbrella sampling windows, each centered at 0.55, 0.57, 0.59, 0.61, 0.62, 0.63, 0.65, 0.67, 0.69, 0.71, 0.73, and 0.75 for each umbrella sampling simulation. We note that three Cremer-Pople ring pucker parameters were needed to fully define glucose ring conformations. Although we chose only one parameter as the reaction coordinate, we examined the other two parameters to ensure that we were sampling from the desired distorted conformation to the chair conformation (supplemental Fig. S1).

The initial conformations of the 12 windows were chosen from a skew-to-chair transition region observed in 10-ns CPHMD simulations conducted at pH 2, 5, and 7 without applying pH-REX for Cel6A and 2.5-ns CPHMD simulations conducted at the same pH values without applying pH-REX for Cel7A (supplemental Fig. S2). Each umbrella sampling window was run for 5 ns in the NPT ensemble. The harmonic force constants on the ring pucker amplitudes were 800 kcal/(mol·Å²) for windows 0.61, 0.62, and 0.63, and 400 kcal/(mol·Å²) for other windows. We chose these force constants to ensure sufficient sampling around the barriers. The weighted histogram analysis method was used to construct the PMF, and the error analysis was conducted with bootstrapping (64).

Loop Flexibility Measurement

Conventional MD simulations (200 ns) with a time step of 2 fs were conducted for Cel6A and Cel7A at pH 5 and 7 by fixing the protonation states of the titratable residues based on the calculated pK_a values. For example, we treated the catalytic acid residue Asp-221 in Cel6A as deprotonated at pH 7 but protonated at pH 5 because its calculated pK_a is 6.41. Considering the possible systematic error, the cutoff pK_a used to determine the protonation state of a titratable residue at solution pH 5 was chosen to be 4.5. This indicates that all of the titratable acid residues with pK_a values larger than 4.5 would remain protonated during the regular MD simulation at pH 5. Specifically, Glu-107, Asp-170, Asp-175, Glu-219, Asp-221, Asp-263, Glu-326, and Asp-366 in Cel6A were protonated, and Asp-173, Glu-190, Glu-193, Asp-214, Glu-217, Glu-223, Asp-257, Glu-295, Glu-317, Glu-325, Glu-334, Glu-335, Asp-368, and Asp-378 in Cel7A were protonated at pH 5. All titratable acid residues were deprotonated during the MD simulation at pH 7. We then measured the root mean square fluctuation (RMSF) of the protein residues in both the free and bound states.

RESULTS AND DISCUSSIONS

pK_a of Key Residues in Cel6A

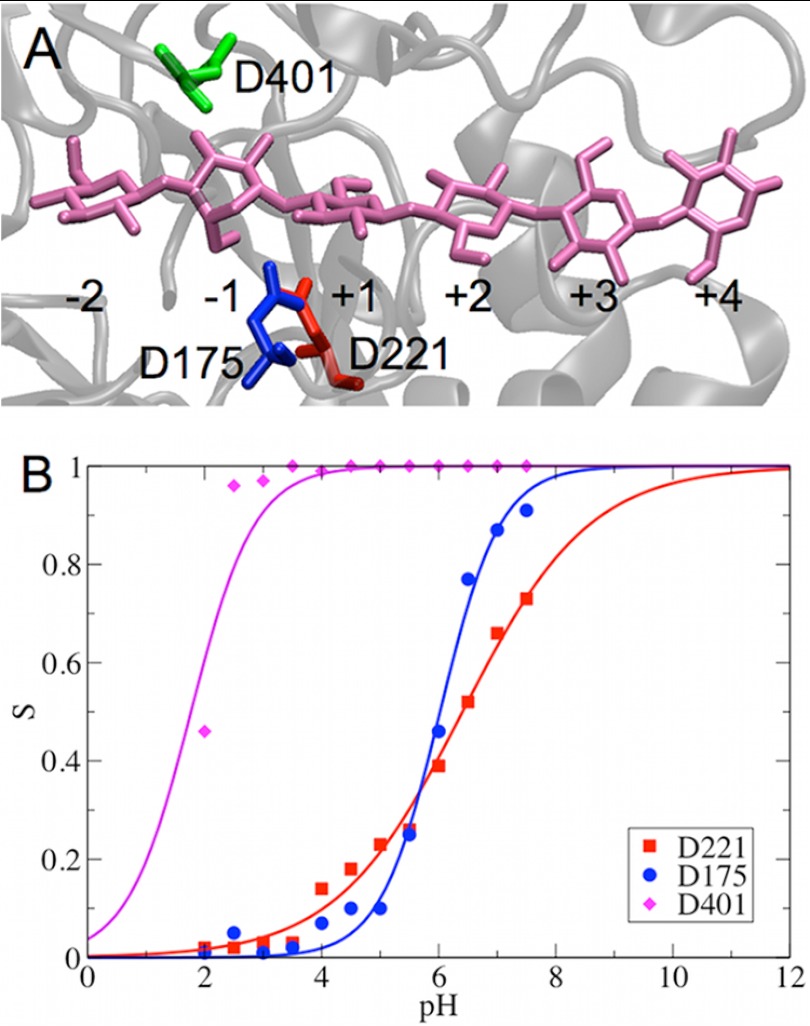
Cel6A hydrolyzes glycosidic bonds via an inverting mechanism (15). Structural studies have suggested that two aspartic residues, i.e. Asp-221 and Asp-175, at the active site of Cel6A are close to the glycosidic oxygen atom and have been observed in some structures to form a hydrogen bond with one another (41, 65). Mutagenesis and enzyme kinetic studies suggest that Asp-221 is the catalytic acid, whereas Asp-175 can affect protonation of Asp-221 and stabilize the transition state (65). The hydrolysis reaction is proposed to involve the following steps from the catalytic resting state: (a) the Asp-221 side chain rotates toward the glycosidic oxygen and breaks the H-bond with Asp-175; (b) Asp-221 transfers its proton to the glycosidic oxygen, breaking the glycosidic bond; and (c) a water molecule, serving as the nucleophile, attacks the anomeric carbon atom. The water proton may be transferred to Asp-175 by proton hopping via another water molecule that has been observed in a Cel6A crystal structure (65). Another aspartic acid, Asp-401, has been suggested to possibly serve as the catalytic base due to its position relative to Asp-221 (66, 67). A close examination of the crystal structure also suggests a low pK_a for Asp-401 due to the numerous hydrogen bonds formed between Asp-401 and the side chains of nearby residues Arg-353, Tyr-306, and Lys-395 (65). However, a structural study suggests that the carboxylate group of Asp-401 interacts with the O3 hydroxyl of glucose at the −1 site (41), indicating that Asp-401 is not a potential catalytic base.

The calculated pK_a values of the key catalytic residues Asp-221, Asp-175, and Asp-401 in Cel6A are summarized in Table 1. The pK_a values of all other titratable acid residues are shown in supplemental Table S1. We also plotted the deprotonation fraction of Asp-221 as a function of time for each pH replica to demonstrate the convergence (supplemental Fig. S3A). The results in Table 1 suggest that the substrate bound in the catalytic tunnel, as shown in Fig. 1A, can significantly affect the pK_a values of the titratable acid residues at the active site. Specifically, the pK_a values of Asp-221 and Asp-175 are shifted to more basic by ∼2 units and ∼1 pH unit, respectively. Because various substrates might have different effects on modifying the pK_a values of the catalytic residues, this offers a potential explanation for the observation that the pH optima of cellulases are also substrate-dependent (68). The calculated titration curves for bound Cel6A are shown in Fig. 1B.

TABLE 1.

Calculated pK_a values of key residues in Cel6A

	pKa
	Asp-221	Asp-175	Asp-401
Without substrate	4.43 ± 0.12	4.91 ± 0.43	1.79 ± 0.03
With substrate	6.41 ± 0.11	6.02 ± 0.06	1.77 ± 0.07

FIGURE 1.

Structure of the catalytic tunnel in Cel6A (A) and titration curve measured for catalytic residues (B). The key catalytic residues are highlighted as red, green, and blue sticks around the cellodextrin, which is shown as mauve sticks. The glucose ring bound at the −1 site exhibits a ²S₀ conformation.

The calculated pK_a values of the key acid residues in the active site enable us to interpret their roles during catalytic hydrolysis. The two apparent pK_a values obtained from the experimentally measured pH-dependent activity profiles of Cel6A are at pH ∼2 and ∼6 (65). The calculated pK_a of Asp-221 in the bound state is 6.41, which is comparable to the apparent pK_a obtained from the basic portion of the pH-dependent activity profile of Cel6A and supports its proposed role as the catalytic acid. The calculated pK_a of Asp-175 is 6.02, which suggests that Asp-175 may not function as a catalytic base at first glance because the pK_a of the catalytic base should be lower than the pH optimum of Cel6A to enable the base residue to be deprotonated and able to accept a proton from the reacting water molecule. However, a detailed examination of the interactions between Asp-221 and Asp-175 indeed indicated that Asp-175 could be deprotonated in the catalytically active state, thus serving as a base to accept a water proton. We discuss the role of Asp-175 in detail below. Our results also suggest that the interactions between the side chain of Asp-401 and the O3 hydroxyl of glucose at the −1 site remain intact during the entire MD simulation, thus supporting the experimental hypothesis of the role of Asp-401 (41). The calculated pK_a of Asp-401 is 1.77, which supports the structural prediction of its pK_a (65).

Asp-221/Asp-175 Interactions in Cel6A

The crystal structure of Cel6A identified that Asp-221 and Asp-175 are at H-bonding distance from each other in the catalytic resting state. Previous MD simulations revealed that the side chain of Asp-221 can rotate away and break the contact with Asp-175, thus bringing the protonated oxygen of Asp-221 closer to the glycosidic oxygen atom with a distance of 3.3 ± 0.3 Å before the hydrogen bond re-forms between Asp-221 and Asp-175 (65). Therefore, side chain rotation of Asp-221 is proposed to be one component of the catalytic mechanism in Cel6A.

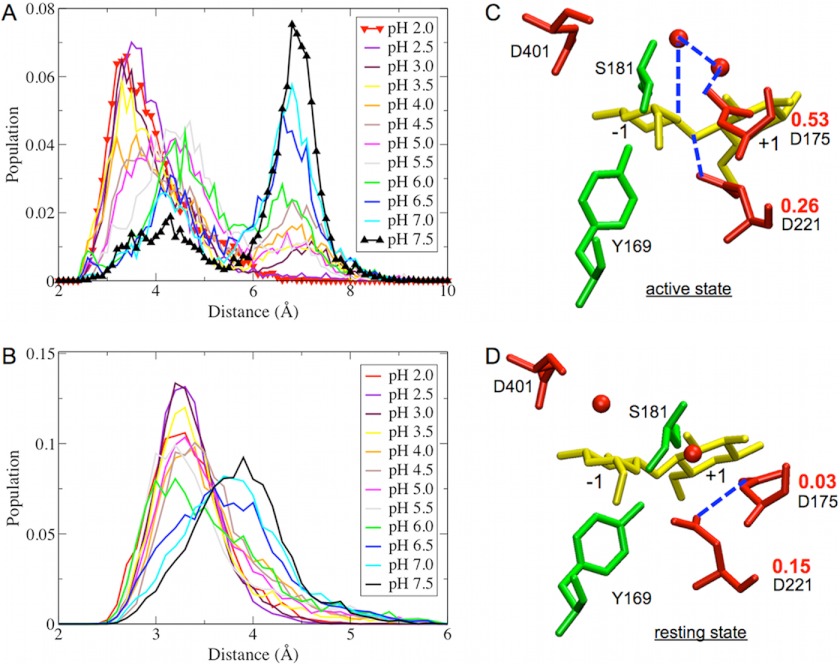
Because the distance between Asp-221 and Asp-175 may have important implications in the Cel6A catalytic activity, we plotted the distributions of the minimum distance between the carboxylate oxygen atoms of Asp-221 and Asp-175 at each solution pH, as shown in Fig. 2A. The 12 peaks cluster into three populations centered at ∼3.5, 4.5, and 7.0 Å. The results suggest that there are strong H-bonding interactions between Asp-221 and Asp-175 in the pH range 2.0–4.0. The interactions of Asp-221 with Asp-175 remain (although they become weaker) at pH 4.5–5.5. In the region of pH 2.0–5.5, the relative population of the state in which Asp-221 interacts with Asp-175 ranges from ∼50 to 85%, as shown in Fig. 3, whereas this population drops to ∼20–35% at pH 6.0–7.5 because both Asp-221 and Asp-175 will be deprotonated at a more basic pH, and the repulsive interactions between the two negatively charged residues thus separate Asp-221 and Asp-175.

FIGURE 2.

Shown are the distributions of minimum distances between Asp-221 and Asp-175 carboxylate groups (A) and Asp-221 and the glycosidic oxygen atom (B). Asp-221 and Asp-175 are catalytic residues of Cel6A. Shown are the structures of the active site in the catalytically active state (C) and in the resting state (D). The deprotonation fractions of Asp-221 and Asp-175 in the two states are shown in red. The blue dashed lines indicate H-bonding distance between two residues. The red spheres are water molecules denoted by the oxygen position (hydrogen atoms not shown).

FIGURE 3.

Integrated probability distribution of the Asp-221/Asp-175 distance from 0 to 4.5 Å in Fig. 2A.

We examined the protonation states of Asp-221 and Asp-175 in the separated clusters identified in Fig. 2A. Specifically, we calculated the deprotonation fraction of Asp-221 and Asp-175 at pH 5 using a subset of the total sampled structures in which the distance between Asp-221 and Asp-175 was either <3.5 Å (resting state) or >7.0 Å (catalytically active state). In the resting state, as shown in Fig. 2D, Asp-221 and Asp-175 form a H-bond, and Asp-221 is far away from the glycosidic oxygen. The deprotonation fractions are 0.15 and 0.03 for Asp-221 and Asp-175, respectively. This indicates that the populations of the protonated states for Asp-221 and Asp-175 are 0.85 and 0.97, respectively, suggesting the both Asp-221 and Asp-175 are protonated in the resting state; thus, Asp-175 cannot act as a base. In the catalytically active state, as illustrated in Fig. 2C, Asp-221 rotates away from Asp-175 to break the H-bond between them and presents itself in H-bonding distance from the glycosidic oxygen. The calculated deprotonation fractions are 0.26 and 0.53 for Asp-221 and Asp-175 in the active state, respectively. The protonation state of Asp-221 does not change significantly overall; however, the protonation state of Asp-175 changes from 0.03 in the catalytic resting state to 0.53 in the catalytically active state. This indicates that 53% of Asp-175 is deprotonated in the active state at pH ∼5, which enhances the ability of Asp-175 to accept a proton and function as a catalytic base. We note that the CPHMD approach treats water molecules as conventional neutral water molecules without additional protons, and thus, we did not investigate the protonation states of the two catalytic water molecules in Cel6A.

The distributions of the minimum distance between the carboxylate oxygen atoms of Asp-221 and the glycosidic oxygen atom of glucose at the −1 site are shown in Fig. 2B. This distance is ∼3.3 Å at pH 2.0–6.0, consistent with the minimum distance observed in previous MD simulation studies (34, 65). The H-bonding distance between the carboxylate oxygen of Asp-221 and the glycosidic oxygen is necessary for the protonation of the glycosidic oxygen by Asp-221. This distance slightly increases to 4.0 Å at pH 6.5–7.5, suggesting that the hydrolysis reaction in Cel6A is less likely to occur beyond pH 6.5.

pK_a of Key Residues in Cel7A

As a retaining cellulase, Cel7A catalyzes the glycosidic bond hydrolysis via a double-displacement mechanism (40, 69), which consists of two steps: 1) the catalytic acid Glu-217 protonates the glycosidic oxygen, and the nucleophile Glu-212 attacks the anomeric carbon to form a glycosyl-enzyme intermediate; and 2) Glu-217, now becoming the catalytic base, deprotonates a water molecule, which then attacks the anomeric carbon likely via an S_N2 reaction and replaces the bond to Glu-212 (70). A third acid residue, Asp-214, is also important for catalysis by possibly attenuating the pK_a of Glu-212 (71).

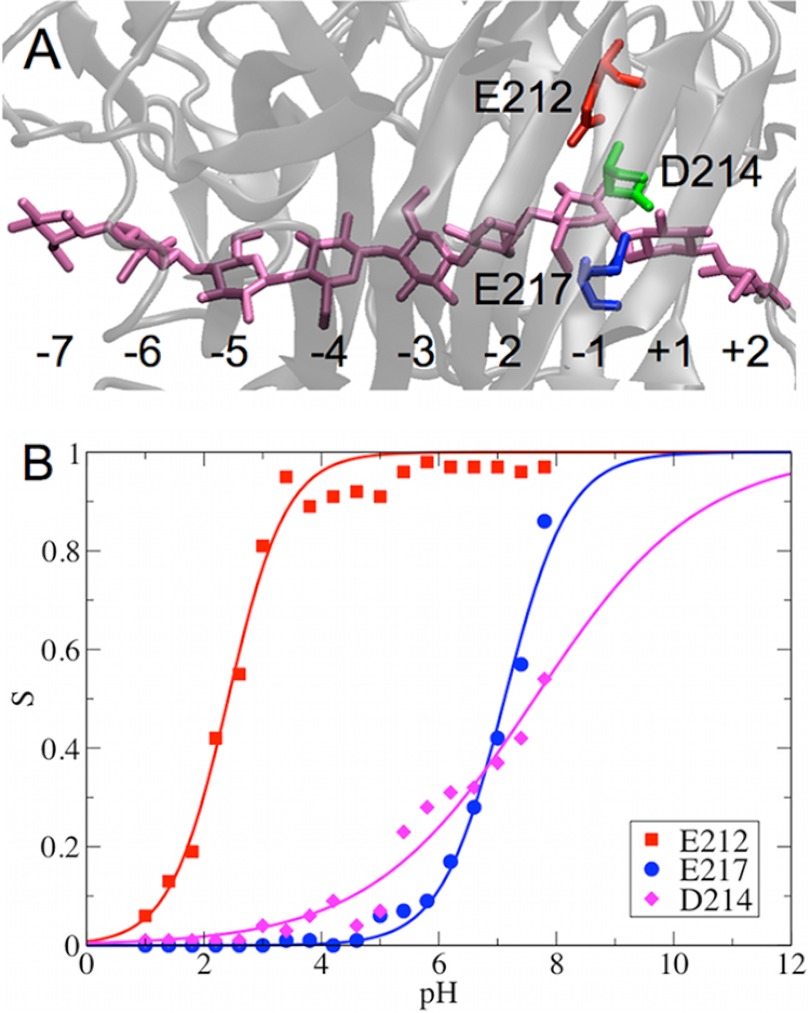
Similar to Cel6A, the substrate bound in the catalytic tunnel of Cel7A, as shown in Fig. 4A, significantly affects the pK_a values of the titratable acid residues at the active site. Specifically, the pK_a of Asp-214 in Cel7A is shifted to more basic by ∼2 pH units (Table 2). The pK_a values of Glu-212 and Glu-217 are shifted toward basic pH by ∼1 unit. The calculated titration curves for bound Cel7A are shown in Fig. 4B. As an additional convergence check, the deprotonation fraction of Glu-217 as a function of time for each pH replica is shown in supplemental Fig. S3B.

FIGURE 4.

Structure of the catalytic tunnel in Cel7A (A) and titration curve measured for catalytic residues (B). The catalytic residues around the substrate are highlighted as red, green, and blue sticks. The substrate is shown as mauve sticks.

TABLE 2.

Calculated pK_a values of key residues in Cel7A

	pKa
	Glu-212	Glu-217	Asp-214
Without substrate	1.41 ± 0.45	5.99 ± 0.36	5.33 ± 0.17
With substrate	2.41 ± 0.32	7.12 ± 0.20	7.63 ± 0.08

The computed pK_a values of the nucleophile Glu-212 and acid/base Glu-217 in Cel7A are 2.41 ± 0.02 and 7.12 ± 0.20, respectively, which are comparable with the apparent pK_a values obtained from experimental measurements of the pH-dependent activity of Cel7A (68). As mentioned above, the experimentally measured pH activity profiles are substrate-dependent. The apparent pK₁ and pK₂ values are 2.22 ± 0.03 and 5.99 ± 0.02, respectively, for 3,4-dinitrophenyl lactoside hydrolysis, whereas these values are 2.94 ± 0.11 and 6.45 ± 0.06, respectively, for 2-chloro-4-nitrophenyl lactoside hydrolysis (68). The small difference between our calculated pK_a values and experimentally measured apparent pK_a values may be due to the different substrates used in the simulations and the experiments. Finally, we note that the calculated pK_a values of Asp-401 in Cel6A and Asp-214 in Cel7A may have larger errors due to less sampling of the protonation states at the boundary regions, i.e. pH 2 is the lower limit used in Cel6A pH-REX simulations, and pH 7.8 is the upper limit used in Cel7A pH-REX simulations.

The fitted Hill coefficients (n), representing the slope of a titration curve, are 0.47 for Asp-221 in Cel6A and 0.31 for Asp-214 in Cel7A, whereas n ranges from 0.80 to 0.88 for the other four catalytic residues. In general, a small value of n indicates that the titration of this residue is strongly coupled to another titratable residue. For instance, the titration of Asp-221 might be coupled to Asp-175 in Cel6A, and the titration of Asp-214 might be coupled to Glu-212 in Cel7A.

PMF for Ring Pucker in Cellulases

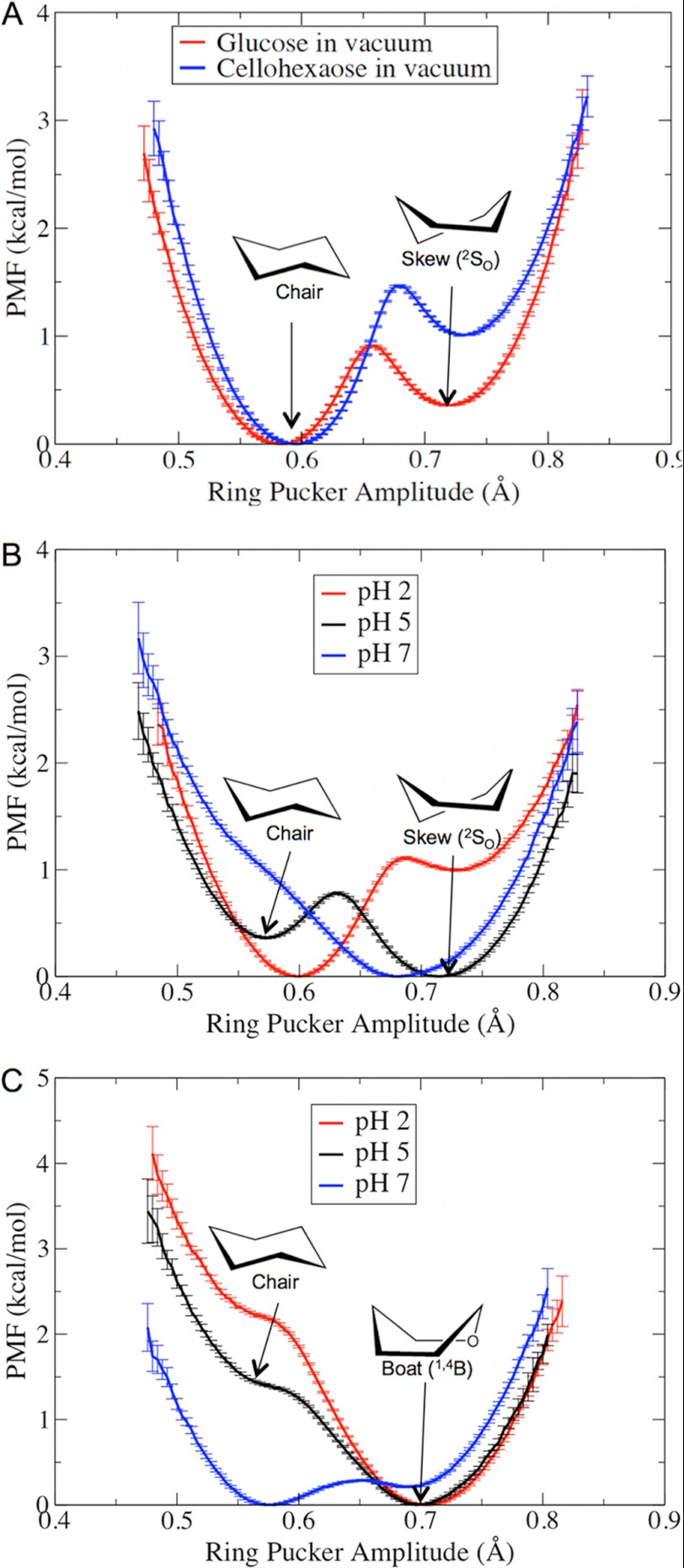
A key step in GH catalysis is the carbohydrate ring distortion at the −1 site (41) to a non-chair conformation, which is thought to prime the ligand for nucleophilic attack. We hypothesized that changes related to the protonation states of the residues around the −1 ligand-binding site will affect the relative thermodynamic stability of the non-chair conformation in both Cel7A and Cel6A. To test this hypothesis, as described below, we conducted free energy calculations to examine the free energy changes in Cel7A from the ^1,4B conformation to the ⁴C₁ chair conformation and in Cel6A from the ²S₀ conformation to the ⁴C₁ chair conformation. However, we first conducted umbrella sampling simulations of ring pucker in a glucose molecule and a cellohexaose molecule in vacuum to determine whether or not the classical force field is able to distinguish that non-chair conformations (from Cel6A) are higher in free energy as has been shown with quantum mechanical calculations (72) and experiments (73, 74). Each umbrella window was run for 100 ns for glucose and 50 ns for cellohexaose. The constructed PMF, as shown in Fig. 5A, suggests that the chair conformation is more thermodynamically favorable for both glucose and cellohexaose molecules in vacuum, as expected. Interestingly, the results also that show a glucose ring located in a cellodextrin chain will prefer a chair conformation more strongly than a single glucose molecule does. A close examination of the other two ring pucker parameters (θ and φ) confirmed that the two stable states observed in Fig. 5A represent the chair and the ²S₀ skew conformations (supplemental Fig. S1, A and B).

FIGURE 5.

PMF of the glucose ring pucker in vacuum (A), at the −1 ligand-binding site of Cel6A (B), and at the −1 site of Cel7A (C) at various solution pH values.

The calculated PMF profiles of the ring pucker at the −1 ligand-binding sites in Cel6A and Cel7A are provided in Fig. 5 (B and C). Computer simulations in Cel6A have shown that the glucose ring at the −1 site cycles between chair and skew conformations, with skew being the energetically favorable conformation (34). Our results suggest that at pH 5, which is the optimal pH for Cel6A, the skew conformation is slightly more thermodynamically favorable than the chair conformation. Additional examination of the other two Cremer-Pople ring pucker parameters (θ and φ) confirmed that the stable skew conformation at pH 5 is ²S₀ and that the less stable chair conformation is ⁴C₁ (supplemental Fig. S1, C and D). At pH 2, the glucose ring is more thermodynamically stable in the chair conformation. At pH 7, although the ²S₀ conformation is also thermodynamically favorable, the pK_a of the catalytic acid Asp-221 suggests that this residue will be most populated in the deprotonated state; thus, Asp-221 cannot provide a proton to the glycosidic oxygen atom.

Similar to Cel6A, our results suggest that at the optimal pH of Cel7A, the glucose at the −1 site favors a distorted conformation, whereas a chair conformation is slightly thermodynamically stable at more basic pH. A distorted conformation is also more thermodynamically stable at pH 2. However, the nucleophile Glu-212 will be mostly protonated at pH 2 based on its pK_a value and thus will be unable to attack the anomeric carbon to form a glycosyl-enzyme intermediate.

There have been several studies on the glucose ring conformation at the −1 site in Cel7A, suggesting possible conformations such as ⁴H₃ (θ = 60°, φ = 210°) and ⁴E (θ = 60°, φ = 240°) (75), as well as ¹S₃ (θ = 90°, φ = 210°) and ^1,4B (θ = 90°, φ = 240°) (76, 77). In this work, we used a theoretical model of Cel7A (Protein Data Bank code 8CEL) consisting of a cellononaose ligand in the catalytic tunnel to construct our model system (14). The structures from our umbrella sampling simulations suggest a ^1,4B conformation for the glucose at the −1 site (supplemental Fig. S1, E and F). We note that because we were using a classical force field, the free energy profiles obtained via umbrella sampling should be interpreted only semiquantitatively.

Loop Flexibility of Cel6A

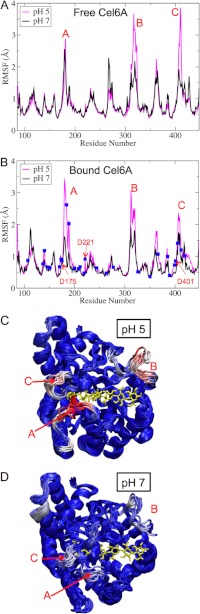
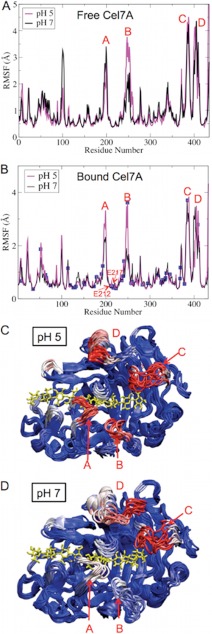
Due to the demanding requirement of CPHMD simulations for computer resources and the necessity of conducting much longer MD simulations to obtain any meaningful information regarding the loop flexibility of cellulases, we performed conventional MD simulations for 200 ns for Cel6A and Cel7A at pH 5 and 7 by fixing the protonation states of the titratable residues based on the calculated pK_a values. The RMSF profiles of Cel6A residues during the 200-ns fixed protonation state MD simulations are shown in Fig. 6. Not surprisingly, the two loops forming the roof of the catalytic tunnel, i.e. loops A and C, are among the most flexible regions in Cel6A. Additionally, loop B, located near the tunnel entrance, also exhibits strong flexibility. The bound substrate stabilizes loops A and C, but it does not affect the flexibility of loop B because the substrate does not directly interact with loop B. It has been hypothesized that some flexibility in the tunnel-forming loops may be important in catalytic engagement and substrate threading in Cel6A (41). Our results illustrate that the active site loops are more flexible at the optimal pH than at neutral pH, which supports the experimental hypothesis (26), and indicate that the loop flexibility also plays a key role in determining the pH optima of cellulases, in addition to the pK_a values of catalytic residues. The pH-dependent flexibility of active site loops is caused by modifications of the protonation states of titratable residues located near these loops, corresponding to changes in solution pH. As demonstrated in Fig. 7, the H-bonding network is significantly modified at these loops, and the number of H-bonds decreases when the solution pH changes from 7 to 5. Protonation of Glu-326 at pH 5 results in the breaking of several H-bonds involving His-266, Asn-307, Ser-316, Tyr-317, and Thr-318. We note that when the pK_a of a titratable residue is close to the solution pH, both protonated and deprotonated states will equally coexist, which is a known limitation of examining flexibility with fixed protonation states.

FIGURE 6.

Shown are the RMSF profiles of Cel6A residues in the free (A) and bound (B) states during 200-ns fixed protonation state MD simulations. The positions of titratable acid residues are shown as blue squares. Snapshots of the Cel6A structures at pH 5 (C) and pH 7 (D) are shown. The color is coded by the β-factor, with blue being the lowest fluctuations to white to red being the highest fluctuations. The bound cellodextrin is shown as a yellow stick model.

FIGURE 7.

Shown is the H-bonding network observed in loops A and C of Cel6A at pH 5 (A) and pH 7 (B) and in loop B at pH 5 (D) and pH 7 (E). Hydrogen atoms were omitted for clarity. The histograms of the number of H-bonds at pH 5 and 7 are also shown for loops A and C (C) and loop B (F).

Loop Flexibility of Cel7A

The RMSF profiles of Cel7A residues during the 200-ns fixed protonation state MD simulations are shown in Fig. 8. The most flexible regions in Cel7A are composed of four loops. The most significant pH-dependent flexibility is observed at loop B, which is more flexible at pH 5 than at pH 7 in both the free and enzymes. Our results thus support the experimental small angle neutron scattering measurements of the solution structure of the CD of Cel7A, which suggested that the Cel7A CD becomes more flexible at the optimal pH (26). We note that the catalytic site of Cel7A is stable regardless of the solution pH, as demonstrated by the small RMSF values of the catalytically important residues Glu-212, Asp-214, and Glu-217.

FIGURE 8.

Shown are the RMSF profiles of Cel7A residues in the apo-state (A) and in the bound state (B) during 200-ns fixed protonation state MD simulations. The positions of the titratable acid residues are show as blue squares. Snapshots of Cel7A structures at pH 5 (C) and pH 7 (D) are shown.

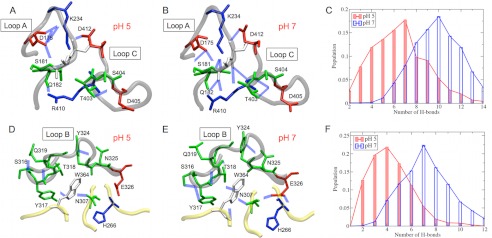
Similar to Cel6A, the pH-dependent flexibility of tunnel loops in Cel7A is also induced by the changing of the protonation states of titratable residues. As shown in Fig. 9, the number of H-bonds decreases as the solution pH changes from 7 to 5. The protonation of Asp-257 at pH 5 results in the loss of several H-bonds involving Ser-248, Arg-251, and Asp-259, which impairs the stability of loop B.

FIGURE 9.

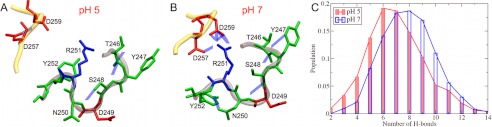
Shown is the H-bonding network in loop B of Cel7A at pH 5 (A) and pH 7 (B) and the histograms of the number of H-bonds at pH 5 and 7 (C).

GH7 cellobiohydrolases have been shown to be able to bind to insoluble cellulose via an endo-initiation mode, creating new chain ends for further processive action (78, 79). A recent computational study of three GH7 cellobiohydrolases suggests that H. jecorina Cel7A exhibits reduced tunnel opening and flexibility compared with Heterobasidion irregulare Cel7A and Phanerochaete chrysosporium Cel7D (80). To investigate the effect of pH on the opening of tunnel-forming loops, which certainly influences enzyme processivity and the likelihood of endo-initiation, we measured the pairwise minimum distance among three loops across the catalytic tunnel, as shown in Fig. 10. The minimum distance between loops B and C increases from 4.3 to 8.2 Å as the solution pH changes from 7 to 5. The minimum distance between loops A and B also slightly increases by 0.6 Å. Additional data showing the histograms of the minimal distances are provided in supplemental Fig. S4. We hypothesized that the increased minimum distance between the tunnel-forming loops at the optimal pH may assist in the initial binding of substrate via endo-initiation mode and subsequent cellodextrin threading, thus enhancing the enzyme activity. Similar observations were also made for Cel6A. The minimal distance between loops B and C in Fig. 7 increases by 1.8 Å as the solution pH changes from 7 to 5, although the minimal distances between loops A and C and between loops A and B slightly decrease by ∼0.2–0.5 Å (supplemental Fig. S5).

FIGURE 10.

A, three loops surrounding the catalytic tunnel of Cel7A. B and C, the minimum distance of loop B from neighboring loops C and A, respectively.

Conclusions

In this work, we have characterized the pK_a values of all titratable residues, including the key catalytic residues in the well characterized H. jecorina cellulases Cel6A and Cel7A. Our results demonstrate that substrate bound in the catalytic tunnel can significantly influence the pK_a values of the titratable acid residues at the active site. A detailed examination of the dynamics of Asp-221 and Asp-175 supports their previously proposed roles, i.e. Asp-221 acts as the catalytic acid, and Asp-175 may function as a base in a proton transfer chain. The calculations also support that Glu-212 is the nucleophile in Cel7A and that Glu-217 acts as catalytic acid/base. Additionally, it has long been recognized that the ring pucker conformation of saccharides in the transition state is a crucial element in the catalytic mechanisms of GHs (40). The calculated free energy profiles of glucose ring pucker suggest that the glucose residue at the −1 ligand-binding site is more thermodynamically stable in the experimentally determined distorted conformations in both Cel6A and Cel7A at the optimal pH. Finally, our results demonstrate that the loops across the catalytic tunnels in Cel6A and Cel7A are more flexible at the optimal pH than at neutral pH, which is due to the modification of the H-bonding interactions induced by the protonation of titratable acid residues located near the tunnel-forming loops, corresponding to changes in solution pH. At the optimal pH, Cel7A exhibits a more open active site tunnel than it does at neutral pH, which may aid in substrate access to the catalytic tunnel. These results provide a molecular-level understanding of the pH-dependent conformation changes in Cel7A as observed in experimental studies (26). Taken together, this work suggests that pH significantly affects the ring pucker conformation of glucose at the −1 site necessary for catalysis and the flexibility of the tunnel-forming loops, the latter which will affect processivity and substrate complexation.