Dynamic interpretation of maternal inputs by the Drosophila segmentation gene network

Abstract

Patterning of body parts in multicellular organisms relies on the interpretation of transcription factor (TF) concentrations by genetic networks. To determine the extent by which absolute TF concentration dictates gene expression and morphogenesis programs that ultimately lead to patterns in Drosophila embryos, we manipulate maternally supplied patterning determinants and measure readout concentration at the position of various developmental markers. When we increase the overall amount of the maternal TF Bicoid (Bcd) fivefold, Bcd concentrations in cells at positions of the cephalic furrow, an early morphological marker, differ by a factor of 2. This finding apparently contradicts the traditional threshold-dependent readout model, which predicts that the Bcd concentrations at these positions should be identical. In contrast, Bcd concentration at target gene expression boundaries is nearly unchanged early in development but adjusts dynamically toward the same twofold change as development progresses. Thus, the Drosophila segmentation gene network responds faithfully to Bcd concentration during early development, in agreement with the threshold model, but subsequently partially adapts in response to altered Bcd dosage, driving segmentation patterns toward their WT positions. This dynamic response requires other maternal regulators, such as Torso and Nanos, suggesting that integration of maternal input information is not achieved through molecular interactions at the time of readout but through the subsequent collective interplay of the network.

The macroscopic patterns of multicellular organisms are established by the molecular interplay within transcription factor (TF) networks that give rise to corresponding patterns of gene expression during the earliest stages of embryonic development (1). During these stages, individual cells acquire information about their position within the embryo by interpreting multiple TF concentration gradients and other factors that are inhomogeneously distributed in the egg (2–5). However, the quantitative and dynamic nature of this interpretation and the subsequent response of the network are not well understood. Specifically, little is known about the ability of individual DNA loci to measure TF concentrations precisely or how these loci integrate information from measurements of multiple input concentrations. One can distinguish between two broad classes of system-level viewpoints of how this information is interpreted by the network. In one view, information-rich maternal gradients provide all the spatial cues for the final patterns and the information is relayed in a step-by-step feed-forward manner, consistent with the traditional threshold-dependent readout model (6). In the other view, maternal gradients provide the initial spatial cues to downstream genes that then cross-regulate in an otherwise self-organized network (7–16).

The Drosophila embryo provides an excellent system in which these problems can be addressed in a physiologically relevant context and the influences from different input factors can be disentangled (4, 5, 17). Soon after the egg is activated, naturally varying protein gradients establish in the developing egg, which are interpreted by zygotic genes in a concentration-dependent manner. One such gradient is the anterior determinant Bicoid (Bcd) (18, 19), whose mRNA is maternally deposited at the anterior pole of the egg (20, 21). Bcd acts as a TF and activates target genes, such as the gap gene hunchback (hb) and the primary pair-rule gene even-skipped (eve) (22, 23). This cascade of regulatory events generates spatial patterns that are precise enough to distinguish neighboring nuclei based on their levels of gene expression (24), and these patterns are reproducible from embryo to embryo (25–28).

If Bcd concentration directly controls cell fate as predicted by the traditional threshold-dependent readout model (6), the Bcd-dependent patterning markers must always form at the same absolute Bcd concentration, even in genetic backgrounds of altered bcd copy numbers of variable strengths (18, 22, 29) (Fig. S1). The cephalic furrow (CF), a morphological feature that separates the head and thoracic region of the early embryo, has provided a useful test for this idea. In embryos with altered bcd copy numbers, the CF’s location along the anterior-posterior (AP) axis shifts with respect to WT, but likely not in a strict concentration-dependent manner (18, 25, 30). However, to test how Bcd is interpreted quantitatively, it is necessary to measure actual Bcd protein concentration instead of relying on the bcd copy number. The expression of bcd could be negatively regulated, and expression levels could vary for exogenous bcd alleles, because transgenes insert randomly in the genome and their expression levels depend on the chromosomal insertion site (31).

To address the above, we generated an allelic series of transgenic fly strains with various absolute Bcd concentrations, exploiting the chromosome position effect (31). Performing precise measurements on embryos of these fly strains, we quantified the expression levels of the various transgenes. We found that multiple insertions in the same embryo add their individual strengths in an entirely linear manner over a fivefold range in Bcd concentration, suggesting no feedback is involved in Bcd expression. When we measure the network’s reaction to fivefold absolute Bcd concentration changes, we observe that the network responds nearly perfectly to Bcd at early developmental stages but subsequently adapts to the dosage alteration, partially restoring the shifted AP patterns to their WT positions. Interestingly, this dynamic process vanishes when these measurements are repeated in flies mutant for other maternal inputs, such as torso (tor) or nanos (nos). These findings suggest that the dynamic response is a result of interacting inputs and that the system achieves integration of positional information from various inputs not by molecular interactions at a specific enhancer when Bcd is turning on genes but through the subsequent downstream interplay of the network.

Results

Generation of 20 Fly Lines with 5.7-Fold Bcd Concentration Changes.

To vary Bcd concentrations, we first generated six Drosophila fly lines to use as founder lines, in which endogenous Bcd is replaced by the bcd^E1 null phenotype and Bcd activity was supplied by a transgene producing a fully functional fluorescent EGFP-Bcd fusion protein (called Bcd-GFP hereafter). We performed live imaging to measure absolute Bcd concentrations and compared nuclear Bcd-GFP gradients across these fly lines. Nuclear Bcd-GFP concentration gradients were extracted from individual embryos in coronal optical sections (Fig. 1 A and B) using a custom-built two-photon microscope with significantly improved signal-to-noise ratios compared with previous measurements (SI Materials and Methods). The gradient reproducibility is ∼15% across almost the entire AP axis, except for the most anterior and posterior ends (Fig. 1C). Statistically, the accuracy with which we can distinguish between Bcd dosages of two fly lines is set by our measurement noise and by the intrinsic reproducibility of Bcd concentrations in a population of embryos, which we determined at 14.5% by the dosage fluctuations within a single fly line (Fig. 1D); thus, the discrimination accuracy in a typical imaging session with a sample size of ∼10 embryos approaches 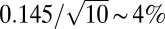. The final Bcd dosage of a typical fly line was measured by comparing its average Bcd-GFP gradient with a concurrently imaged average Bcd-GFP gradient of a reference fly line named 2X_A (Fig. 1E and SI Materials and Methods), whose Bcd concentration is close to the endogenous WT Bcd concentration (see below). The Bcd dosages of the six founder lines range from 0.77 to 1.09, with an average measurement error of 7 ± 2% (Fig. 1E, Inset).

Fig. 1.

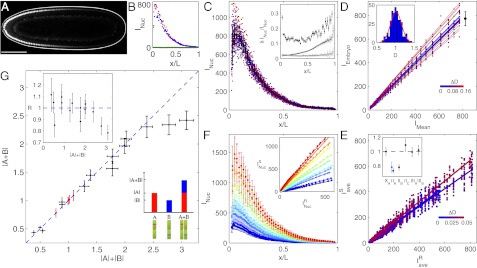
Absolute Bcd-GFP concentration and dosage measurements. (A) Scanning two-photon microscopic image of a Drosophila embryo (dorsal view of midcoronal plane) expressing a Bcd-GFP fusion protein (reference fly line 2X_A; described in the main text). (Scale bar: 100 μm.) (B) Apparent Bcd-GFP nuclear intensity, I_Nuc, in each visible nucleus in A plotted vs. AP position x in units of egg length L; the left and right sides of the AP axis are shown in red and blue, respectively (∼70 nuclei each). The background (green) is measured in 12 WT embryos (same imaging conditions). (C) Nuclear Bcd-GFP intensities of 2X_A embryos measured in a single imaging session (different colors for 21 individual embryos); means and SDs of nuclei in 50 equidistant bins are shown in black. (C, Inset) For each bin, the SD, δI_Nuc, divided by the mean I_Nuc is shown as a function of fractional embryo length x/L (dark points); error bars are determined from bootstrapping. Dark and light gray curves show imaging noise and image processing error, respectively. (D) Scatter plots (dots) and linear fits (lines) of embryo intensity, I_Embryo (I_Nuc of each of the 21 binned Bcd-GFP gradients in C) vs. mean intensity, I_Mean [average binned Bcd-GFP gradient (black curve in C)]. The slope of each linear fit defines the dosage D of an individual embryo, relative to the average Bcd dosage of the given fly line. Color encodes fractional change from mean dosage D = 1 (color bar). The black error bar represents dosage spread in this particular imaging session (σ = 8%). (D, Inset) Histogram of 360 single-embryo dosages (2X_A embryos, 33 imaging sessions). The red line is a Gaussian fit with an SD of 14.5%. (E) Dosage measurement of sample fly line 2II_A. Different colors correspond to four independent imaging sessions. Dots are 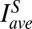(binned means of nuclear Bcd-GFP concentrations of individual embryos) plotted against 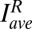(average binned mean nuclear Bcd-GFP concentration of the reference fly line 2X_A) measured side by side in the same imaging session. The dosage extracted per imaging session from the slope of a linear fit (solid lines) is D = {0.73, 0.71, 0.70, 0.78}. Color encodes the fractional change from the mean dosage D = 0.73 ± 0.03 for the four sessions (color bar), implying a dosage reproducibility of ∼4%. (E, Inset) Average dosage for 6 homozygous fly lines with respect to dosage D = 1 (dashed line). Black data points correspond to a single fit to the combined data of all imaging sessions; error bars are determined from bootstrapping. For fly line 2II_A, a linear fit to data from pooled imaging sessions (light blue) and the average of linear fits to individual imaging sessions (dark blue) are shown. (F) Average binned Bcd-GFP gradients of 11 fly lines with Bcd-GFP dosages as indicated in Table S1; error bars are across all nuclei of all embryos in a given bin. (F, Inset) Linear fits to scatter plots of average Bcd-GFP gradients of the sample fly lines compared with the average Bcd-GFP gradients of the reference fly line 2X_A. The “+” symbol depicts average of data in E. (G) Scatter plot of measured Bcd-GFP dosage 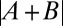of fly line A + B and the expected Bcd-GFP dosage 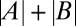from individual measurements of fly lines A and B. The means and SDs of the measured Bcd-GFP dosage of the 6 founder lines and the 14 genetically constructed fly lines are shown in red and black, respectively. Vertical error bars correspond to uncertainty in dosage determination. Horizontal error bars are obtained from error propagation (SI Materials and Methods). The blue dashed line shows 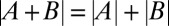. (G, Inset) Deviation from 1 of the ratio 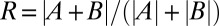is less than 20% for all fly lines.

Using these 6 founder lines, we generated a series of 20 Bcd-GFP expressing fly lines by genetic combination (Fig. 1F and Table S1). The copy numbers of egfp-bcd transgene insertions range from one to six, and Bcd dosages relative to WT span a range of 0.44–2.4, which is well within the linear range of our imaging setup (Fig. S2). Taking advantage of the small dosage differences between the founder lines, the relative increment of the Bcd dosage is comparable to the variability of the Bcd concentration within individual fly lines (Fig. 1D), allowing us to tune Bcd dosage systematically over an almost sixfold range with very fine (<10%) discrete steps. As a result, we have created an effective tunable parameter of input concentration that changes in precise and discrete quantities, comparable to the well-known inducible systems in yeast or bacteria (32). Note that as the absolute Bcd concentration changes across fly lines, neither the shape nor the reproducibility of the gradients changes significantly (Fig. S3). However, in our live Bcd-GFP measurements, the delayed EGFP maturation alters the shape of the Bcd gradient slightly, increasing the mean length constant by ∼15% (SI Materials and Methods and Fig. S4).

Multiple bcd Alleles Operate Perfectly Linearly.

To check whether there is a range around the WT dosage where dosage perturbations are linear and whether individual alleles operate independently, we tested our genetically constructed fly lines arithmetically. We evaluated whether the sum of two fly lines A and B with dosages |A| and |B| is identical to the dosage |A + B| measured in the fly line A + B that is the genetic composition of the two individual lines (cartoon in Fig. 1G). Surprisingly, for the 14 combined fly lines we tested, all data points within the dosage range of 0.44 and 2.3 fall within error bars on the blue dashed line of |A + B| = |A| + |B|, and the ratio of measured to expected dosages is within 20% of unity (Fig. 1G). Thus, the amount of Bcd produced in the combined fly line A + B is the exact summed amount of Bcd produced from the individual fly lines A and B. Only for the two largest dosages that we constructed, 2.34- and 2.4-fold the reference dosage, did we observe a deviation from the diagonal, with predicted dosages of 2.8 and 3.1, respectively. These measurements demonstrate a fivefold physiological dosage range in which Bcd concentrations can be linearly manipulated, allowing us to probe the network’s response to absolute input concentration in a quantitative, systematic manner.

These results indicate that Bcd expression levels are set by a simple linear feed-forward mechanism, and that the amount of Bcd protein produced from each bcd allele in the genome is independent of any of the other bcd alleles present in the same genome. This suggests that the extraordinary reproducibility of the Bcd gradients observed above and in previous work (28) is unlikely to involve any feedback regulation on Bcd expression. We can essentially exclude mechanisms involving Bcd autoregulation that could lead to the precise control of (i) the number of bcd mRNA deposited during oogenesis or (ii) the number of Bcd protein molecules produced during the early stages in the zygote. It further means that in the identified linear range, the system must be devoid of any adjustment scheme that would shift dosage levels back to a WT set point. No limiting factor is present in the system, which would lead to a saturated operation level in setting up the Bcd source, and hence would not be able to cope with too much or too little Bcd in the system.

Quantitative Measurements of CF Shifts on Absolute Bcd Concentration Changes.

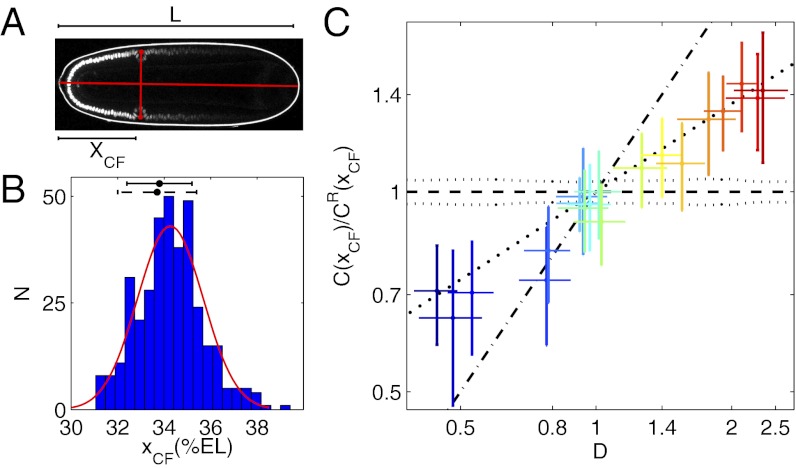
Classically, the most straightforward way to assess the effect of bcd copy numbers on the downstream gene regulatory network is to quantify the location of the CF (18, 33). Here, we follow this traditional approach but ask whether the absolute Bcd concentration in cells of the forming CF is unchanged in fly lines with different overall Bcd dosage. The CF appears at the onset of gastrulation as a change in shape and apical positioning of a single row of cells. Genetically, the position of the invaginating cells is defined by the overlapping expression of two Bcd targets: the head gap gene buttonhead and eve (34). This position can be easily determined either directly by bright-field microscopy or, as in our case, by residual Bcd-GFP that remains in anterior nuclei during gastrulation (Fig. 2A). Thus, conveniently, Bcd gradients and CF positions can be measured in the same embryo, developmentally separated by ∼50 min.

Fig. 2.

CF position measurements and response to Bcd dosage perturbations. (A) Scanning two-photon microscopic image of the same Drosophila embryo as in Fig. 1A, ∼1 h later in its development. The CF position is defined relative to embryo length L as x_CF = X_CF/L, where X_CF is the distance from the anterior pole to the intersection between the AP axis and the line connecting left and right CF invaginations (red dots, manually selected). (B) Histogram of x_CF of 364 2X_A embryos. The red line is a Gaussian curve plotted with the corresponding distribution mean (34.3%EL) and SD (1.2%EL). The CF positions measured by bright-field microscopy (dorsal view) for 2X_A (dark dashed error bar) and WT embryos (dark error bar) are 33.7 ± 1.7%EL and 33.8 ± 1.4%EL, respectively. Experimental measurement errors (0.3–0.6% EL) are illustrated in Fig. S5. (C) Log-log plot of the relative Bcd-GFP concentration at CF positions, C(x_CF)/C^R(x_CF), as a function of Bcd dosage D for 20 fly lines. C(x_CF) and C^R(x_CF) are Bcd-GFP concentrations at the CF position of the sample fly line and the reference fly line 2X_A, respectively. Error bars are SDs of relative C(x_CF) (vertical) and D (horizontal). Different colors represent different fly lines. The slope of the linear fit (bold dotted line) to 1,187 single embryo data points is 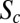= 44 ± 2% (R² = 0.74). Dashed and dotted lines, respectively, show the expected means and SDs of relative C(x_CF) in a scenario in which C(x_CF) is unchanged in the different dosage backgrounds. The dash-dotted line shows the expected relative C(x_CF) if CF location is independent of Bcd dosage.

To measure the location of the CF (x_CF) reliably, great control has to be exerted on embryo orientation and on the exact timing of the measurement (SI Materials and Methods and Fig. S5). Systematic errors are minimized when embryos are imaged from a dorsal view in the coronal plane (Fig. 2A). Under these conditions, we obtained a value of x_CF = 34.3 ± 1.2% embryo length (EL) for our reference fly line 2X_A (Fig. 2B), which is nearly identical to the WT (Oregon-R) CF position of 33.8 ± 1.4%EL, measured via bright-field microscopy (Fig. 2B). The latter agreement justifies our assessment that the Bcd dosage in fly line 2X_A is very close to the endogenous WT Bcd dosage.

A direct test of whether changing the Bcd concentration is equivalent to changing the position is to test whether the Bcd concentration at x_CF, C(x_CF), remains constant on changes in Bcd dosage D in the different fly lines. Fig. 2C shows a log-log plot of the measured maturation-corrected mean and SD of relative C(x_CF) as a function of D for 20 fly lines (SI Materials and Methods and Fig. S6A). We detect a quasilinear relationship with a slope S_C = 44 ± 2% that deviates significantly from zero, the value predicted for the unchanged concentration readout. The magnitude of S_C expresses the deviation of C(x_CF) of a sample fly line with a particular overall Bcd dosage from the expected C(x_CF) as measured in the reference fly line 2X_A. Thus, over the fivefold change in D, we measure only a twofold change in the response, suggesting that the network adapts, but not perfectly. This means that shifts in the position of the CF are reduced compared with predicted values from the unchanged concentration readout (Fig. S6B), confirming previous qualitative observations (18, 25). Overall, these results indicate that the naive assumption that changes in position and in concentration space are equivalent holds only to within a factor of 2. However, it remains unclear whether this discrepancy is informative about the general functioning of the system.

Segmentation Network Responds Dynamically to Bcd Dosage Alterations.

The CF is a positional marker that is regulated by the segmentation gene network and only generated at the end of the maternal/gap/pair-rule gene cascade. This raises the question of whether we also observe a relationship for the earlier underlying gene expression patterns similar to the one we discovered between Bcd concentrations in CF-forming cells and the overall Bcd dosage. If the fate and position of the CF reflect the initial reading of the Bcd gradient, we also expect to see the same twofold change in Bcd concentration at the early patterning boundaries of the gap and pair-rule genes. On the other hand, if the initial response is perfectly concentration-dependent, we expect to see Bcd concentrations at these positions to vary only within 0.1-fold (or 10%; i.e., the limit set by the precision of our measurements).

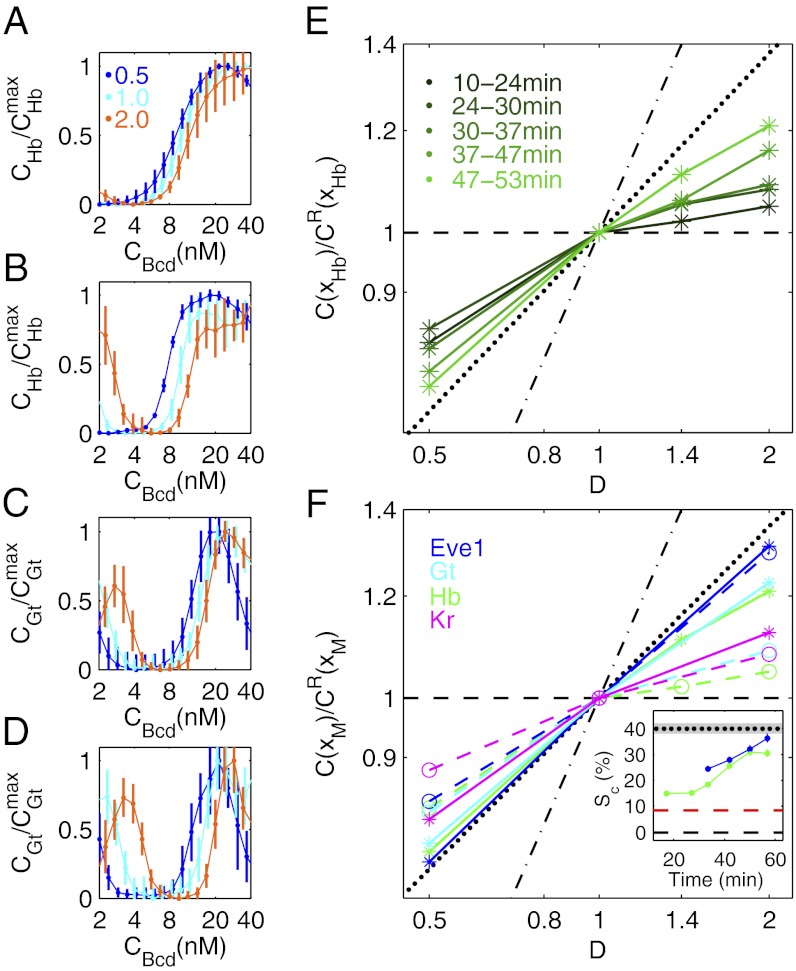
To address this question, we measured the effective input-output relationships between Bcd and the gap genes in fly lines with differing Bcd-GFP dosages. Fig. 3 A–D shows representative input-output functions for the gap genes Hb and Giant (Gt) for early and late time points in nuclear cycle (n.c.) 14. Interestingly, the functions evolve with time. At early stages, they generally tend to overlap and are independent of overall Bcd dosage. At later stages, the gaps between the different dosage curves widen, suggesting an overall dynamic response of the gap gene network. Dynamic gap gene expression patterns have been reported previously (9, 13, 16, 35); the dynamic we observe here, however, is specific in that it is a response to altered overall input dosage.

Fig. 3.

Dynamic network response to Bcd dosage alterations. Average input-output relations of gap genes hb (A and B) and gt (C and D) as a function of input Bcd concentration for three Bcd dosages D: 0.5 (blue), 1.0 (cyan), and 2.0 (orange). Hb and Gt concentrations (C_Hb and C_Gt) are extracted from immunofluorescence profiles of fixed embryos, staged using the invagination depth of the membrane furrow (35), and normalized by the respective maximum concentrations, 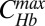and 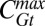. Profiles are shown for n.c. 14 stages at 8–24 min (A and C) and at 47–53 min (B and D). Error bars are SDs in bins of size 3%EL. (E) Log-log plot of relative Bcd-GFP concentration at the Hb boundary, C(x_Hb)/C^R(x_Hb), as a function D. Embryos are separated into five time classes (10–24 min, 24–30 min, 30–57 min, 37–47 min, and 47–53 min) into n.c. 14, shown as shades of green. Black lines are as in Fig. 2C. (F) Log-log plot of relative Bcd-GFP concentrations at four representative segmentation marker positions as a function of Bcd dosage D, including the most anterior peak of the expression pattern of Eve (blue), the posterior boundaries of anterior patterns of Gt (cyan) and Hb (green), and the posterior boundary of Kr (magenta). The dashed and solid colored lines are for early (12 ± 7 min; Eve at 34 ± 3 min) and late (50 ± 3 min) n.c. 14, respectively. Black lines are as in E. (F, Inset) Time dependence of the slope 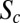for x_Hb (green) and x_Eve1 (blue) (extracted from Fig. S6D; SI Materials and Methods). For comparison, the black dotted line (gray zone) is the average (SD) of the final slope for the CF (linear fit in Fig. 2C and Fig. S6B; SI Materials and Methods). The red dashed line shows 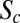for the CF of maternal mutant fly lines (Fig. S6C). The black dashed line is expectation from the threshold-dependent readout model.

We can make this observation more quantitative by measuring Bcd concentration at the location of the posterior boundary of the anterior Hb pattern, C(x_Hb), for the different Bcd dosages (SI Materials and Methods and Figs. S7 and S8). Early during n.c. 14, regardless of the dosage background, C(x_Hb) is very close to the Bcd concentration of cells at x_Hb in a WT background (Fig. 3E), as expected within a threshold-dependent readout model (6). However, as development progresses, relative C(x_Hb) continually changes toward the relative Bcd concentrations in cells of forming CFs, as portrayed in Fig. 2C and shown by the dotted lines in Fig. 3 E and F. This change demonstrates a dynamic response of the Hb profile to altered Bcd input dosages. On a fourfold Bcd dosage change, the change of C(x_Hb) is only 0.3-fold (or 30%) early in n.c. 14, and it keeps increasing to reach a 1.6-fold change later in n.c. 14. Consequently, in altered Bcd dosage backgrounds, the Hb pattern boundaries are continuously driven toward their WT locations by a dynamic process (Fig. S7D). We notice that originally anteriorly shifted boundaries for D < 1 migrate posteriorly and originally posteriorly shifted boundaries for D > 1 migrate anteriorly. The more the Bcd dosage is altered, the more relative shifts occur as development progresses.

Fig. 3F summarizes the changes in Bcd concentrations at particular positions of several representative segmentation markers, including Hb, Gt, Krüppel (Kr), and Eve (the equivalent plot for the CF position is shown in Fig. 2C). For early Gt and Kr profiles, fourfold dosage changes leave Bcd concentrations at the respective boundaries nearly unchanged (within 27% and 23%, respectively). In later stage n.c. 14 embryos, Bcd concentrations at the gap gene boundaries have changed by as much as those of CF-forming cells, as can be seen by the similarity in their respective slopes. We see a similar dynamic evolution for the effective Bcd concentration readout of cells defining stripe 1 of the Eve pattern (Eve–Stripe-1), which, as expected, coincides with the CF at late n.c. 14 stages (Fig. 3F).

Maternal Factors Contribute to Dynamic Adjustments.

To uncover the mechanism underlying the observed dynamic adjustments of the segmentation gene network on Bcd dosage changes, we measured the network response in genetic backgrounds of null mutations for the maternal genes torso-like (tsl) and/or nos, which provides positional information independent of Bcd. Because tsl is required to trigger the activation of Tor receptor tyrosine kinase, disabling tsl blocks Tor function. Although Bcd, Nos, and Tor belong to anterior, posterior, and terminal maternal coordinate systems, respectively, there are several lines of evidence that they do not work independent of each other (4, 5, 17, 36). Therefore, Tor and/or Nos could indeed contribute to the observed dynamic changes of the anterior segmentation markers.

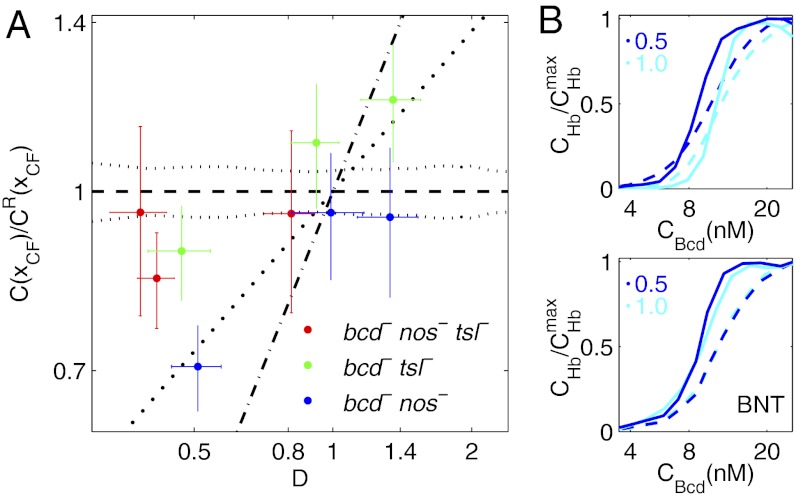
We repeated our CF measurements in fly lines that carry a null mutation for tsl and/or nos and have Bcd dosage backgrounds ranging from 0.4- to 1.4-fold the WT dosage (Table S1). Fig. 4A shows Bcd concentrations at CF positions vs. Bcd dosage measurements in nine of such maternal mutant fly lines. The fly lines in a tsl-null background (green data points in Fig. 4A) have Bcd concentrations in CF-forming cells that are independent of overall dosage for D < 1 (i.e., they fall close to the black dotted line corresponding to WT Bcd concentrations at that particular position). Hence, the effect that we saw in WT backgrounds of altered effective Bcd concentrations has vanished. This result is confirmed in the double-null mutant for tsl and nos (red data points in Fig. 4A). On the other hand, disabling nos only is insufficient to cause the effect to disappear (blue data points in Fig. 4A). These results indicate that for D < 1, the maternal factor Tsl, but not Nos, contributes to the Bcd concentration adjustment at the CF location on Bcd dosage changes, leading to larger positional CF shifts than in the WT case (Fig. S6C). Therefore, tsl has a likely role in the observed dynamics of the segmentation gene network, and multiple maternal inputs are integrated over time to generate the final state of the system. Remarkably, we see a similar, albeit weaker, effect for D > 1; in this regime, however, the roles of nos and tsl seem to be inverted, which may simply indicate that for posterior boundary shifts, it is the maternal Nos gradient that influences the system more significantly than the posterior Tor gradient.

Fig. 4.

Network response to Bcd dosage alterations in maternal mutant backgrounds. (A) Log-log plot of the relative C(x_CF) vs. Bcd dosage D for fly lines carrying various copies of the Bcd-GFP transgene in maternal mutant backgrounds. Red, green, and blue data points represent means and SDs of C(x_CF) normalized by C^R(x_CF) of the reference fly line 2X_A (vertical error bar) and Bcd dosage (horizontal error bar) of fly lines with the maternal mutations bcd^E1nos^BNtsl⁻, bcd^E1tsl⁻, and bcd^E1nos^BN, respectively. The black lines correspond to their identical counterparts in Fig. 2C, which are in a bcd^E1 mutant background. (B) Comparison of the dynamic response of the Bcd-Hb input-output relations to Bcd dosage perturbations [D = 0.5 (blue) and D = 1 (cyan)] in a bcd^E1 background (Upper) and in a bcd^E1nos^BNtsl⁻ (BNT) mutant background (Lower). Hb concentration 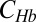is normalized by its maximum value 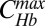. Dashed and solid lines are Bcd-Hb input-output relations extracted from embryos at 8–24 min and at 47–53 min into n.c. 14, respectively.

We further confirmed that the dynamic response of the segmentation network indeed vanishes when the maternal factors Tor and Nos are both nonfunctional. Fig. 4B shows a comparison of the effective input-output relationships between Bcd and Hb. In contrast to fly lines with WT background, the fly lines carrying double-null mutations for both tsl and nos have overlapping effective input-output functions under different Bcd dosage backgrounds at both early and late developmental stages. Together, these data suggest that the observed dynamic changes in concentration interpretation are the result of multiple inputs.

Discussion

One potential origin of the observed dynamic adjustment lies in a dynamic integration of maternally provided positional information by the segmentation gene network (10, 37, 38). At early developmental stages, initial gap gene expression boundaries are solely determined by maternal factors. The posterior boundaries of Hb and Gt are determined by the activation of Bcd, whereas the anterior boundaries of Knirps (Kni) and Kr are determined by the repression of maternal Hb, which is regulated by Nos (39). As development progresses, however, accumulated gap gene products engage in cross-regulation (39) and mediate the integration of positional information of multiple independent maternal factors at the various boundary interfaces. This mechanism could restrict shifts of one boundary resulting from a particular maternal factor by the opposing boundary. Hence, the observed dynamic adjustment could function as an intrinsic mechanism to reduce variability of shifting segmentation patterns due to perturbations by maternal inputs, which is consistent with the increased variability of the posterior Hb boundary in Kr and kni double mutants (8). Together, these findings suggest that neither maternal factors nor the gap genes alone are sufficient for the reduction of the boundary variability; instead, a collective synergy of the entire segmentation gene network is needed. More interestingly, the observed dynamic adjustment mechanism suggests that this network integrates positional information from different maternal factors not by a direct molecular interaction at a particular time point of readout but via a dynamic interplay among the downstream components that occurs at a slightly later stage and also on a slower time scale.

According to a faithful, simple threshold-dependent readout (SI Materials and Methods and Fig. S1A), the concentration at a boundary position on altered Bcd dosage should be unchanged. However, we observe that the relative Bcd concentration at the location of the CF is higher than expected for increased Bcd dosage, and vice versa (Fig. 2C). Quantitatively, it follows a quasilinear relationship 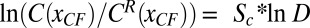with a slope of 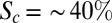instead of 0% as predicted by the simple threshold model. Sixty-three percent of this discrepancy can be attributed to the observed dynamical adjustment, as demonstrated by the adjusted relative Bcd concentration at the Hb boundary and at the position of Eve–Stripe-1 during n.c. 14 (Fig. 3F, Inset). Multiple scenarios are possible for the remaining 37%. The observed dynamics of the downstream genes are prone to begin earlier than at 10 min into n.c. 14, when we can measure them reliably (during n.c. 13, when boundaries are significantly shallower, we were unable to measure with sufficient accuracy and our data remain inconclusive), making them likely major contributors to the observed discrepancy. Nevertheless, we expect the total contribution of the dynamics to be less than ∼80%. In the case of the maternal mutants, when no dynamic adjustments are observed, 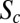is still ∼9% (Fig. S6C), setting a bound on the impact of the dynamics. The remaining discrepancy could result from, for example, combining multiple inputs from a system of repressors for Bcd-regulating genes (5) or a pre–steady-state decoding of Bcd gradients (40). Both mechanisms could contribute to reduce the variability of the segmentation patterns on Bcd dosage perturbations before the dynamic adjustment mechanism is engaged. Future experiments will be needed to clarify if dynamic adjustments, the repressor system, and pre–steady-state decoding are indeed mechanistically unrelated or if they are, in fact, dependent on the combinatorial influence of the maternal products.

Even though our data indicate that the initial response to Bcd could be consistent to within less than 10% with an absolute concentration-dependent readout acting above a predefined threshold (6), the subsequent dynamic adjustment of the boundary location suggests that the Bcd concentration at the final location is no longer relevant; it was the Bcd concentration at the earlier time point when it was first read out that most mattered. Its influence on the network becomes less important as the activity of the gap genes kicks in. This supports the view that maternal gradients provide the initial spatial cues to a network of cross-regulatory interactions between otherwise self-organized downstream genes (5, 18). In this context, the measured precision of the input gradients, such as Bcd (28), remains intriguing, given that the downstream network could, in principle, correct for potential fluctuations (8, 9), as shown by our study. We speculate that something about the concentration set point at the early Bcd readout must be a critical cue for the system and will require further investigation.

The perturbations that we are able to measure here point to a fundamental and unique understanding about the interpretation of TF concentrations. We are able to observe such subtle effects only because we are applying a physics approach based on highly precise measurements to biological specimens. For example, improvements in imaging were necessary to see nuclei containing Bcd-GFP all the way to the posterior end, leading to a dramatic reduction in systematic errors in low nuclear Bcd concentration measurements. Because of this reduction, we were able to show that gradient reproducibility is greatly increased in the posterior half of the embryo, a major prerequisite, together with identical length constants and reproducibility across different fly lines (Fig. S3), for our dosage measurements.

The series of fly lines that we have generated with both large and very small changes in absolute Bcd concentrations will prove to be a very useful tool not only to study the general properties of protein gradients but to investigate quantitatively the responses of the ensuing genetic network. Quantification of the responses to subtle input concentration perturbations can finally lead us to establish very “fine-grained” quantitative models operating at the biophysical “TF-DNA level” (41), surpassing the qualitative “coarse-grained” model from the traditional genetic mutation experiment that always has the potential to cause severe network changes. Our study has provided unique challenges for modeling attempts of the segmentation gene network that can faithfully reproduce gap gene dynamics in a WT setting (9). Our data reveal boundary shifts of the gap genes under altered Bcd input dosage conditions and a dynamic readjustment of the shifted boundaries toward their WT locations. Current models (7, 9, 30, 40) cannot reproduce these features, and a new generation of models is necessary to account for all available data.

Materials and Methods

Both Bcd-GFP gradients and CF positions were measured with live imaging using two-photon microscopy. The expression profiles of Bcd target genes were detected on immunostained embryos. More details are provided in SI Materials and Methods.