APPLYING TENSOR-BASED MORPHOMETRY TO PARAMETRIC SURFACES CAN IMPROVE MRI-BASED DISEASE DIAGNOSIS

Abstract

Many methods have been proposed for computer-assisted diagnostic classification. Full tensor information and machine learning with 3D maps derived from brain images may help detect subtle differences or classify subjects into different groups. Here we develop a new approach to apply tensor-based morphometry to parametric surface models for diagnostic classification. We use this approach to identify cortical surface features for use in diagnostic classifiers. First, with holomorphic 1-forms, we compute an efficient and accurate conformal mapping from a multiply connected mesh to the so-called slit domain. Next, the surface parameterization approach provides a natural way to register anatomical surfaces across subjects using a constrained harmonic map. To analyze anatomical differences, we then analyze the full Riemannian surface metric tensors, which retain multivariate information on local surface geometry. As the number of voxels in a 3D image is large, sparse learning is a promising method to select a subset of imaging features and to improve classification accuracy. Focusing on vertices with greatest effect sizes, we train a diagnostic classifier using the surface features selected by an ℓ₁-norm based sparse learning method. Stability selection is applied to validate the selected feature sets. We tested the algorithm on MRI-derived cortical surfaces from 42 subjects with genetically confirmed Williams syndrome and 40 age-matched controls, multivariate statistics on the local tensors gave greater effect sizes for detecting group differences relative to other TBM-based statistics including analysis of the Jacobian determinant and the largest eigenvalue of the surface metric. Our method also gave reasonable classification results relative to the Jacobian determinant, the pair of eigenvalues of the Jacobian matrix and volume features. This analysis pipeline may boost the power of morphometry studies, and may assist with image-based classification.

1. INTRODUCTION

Computer-assisted diagnostic classification is becoming increasingly popular in neuroimaging, especially given the vast number of features available to assist diagnosis in a 3D brain image. Early diagnosis and treatment of degenerative brain diseases, such as Alzheimer’s disease, depends on the ability to identify disease in its earliest stages, when brain changes may be subtle. In addition, there is interest in understanding which brain imaging features are best for diagnostic classification, as well as biomarkers to measure the severity of disease burden. Over the last decade, many methods have been proposed to study the problem of diagnostic classification based on structural magnetic resonance imaging (MRI) (Golland et al., 2001; Yushkevich et al., 2003; Fan et al., 2007; Vemuri et al., 2008; Gutman et al., 2009; Sun et al., 2009a; Xiang et al., 2009; Cuingnet et al., 2010; Cuingnet et al., 2011; Sabuncu and Van Leemput, 2011; Batmanghelich et al., 2012), positron emission tomography (PET) (Chen et al., 2011; López et al., 2011), single photon emitting computer tomography (SPECT) (Fung and Stoeckel, 2007) or a combination of multi-source datasets (Calhoun and Adali, 2009; Chen et al., 2009; Correa et al., 2010; Jack et al., 2010; Kohannim et al., 2010; Yang et al., 2010; Groves et al., 2011; Sui et al., 2011; Yuan et al., 2012). Surface-based modeling is useful in brain imaging to help analyze anatomical shapes, to detect abnormalities in cortical surface folding and thickness, and to statistically combine or compare 3D anatomical models across subjects (Drury et al., 1996; Thompson and Toga, 1996; Fischl et al., 1999; Vaillant et al., 2007; Yeo et al., 2008; Wang et al., 2010c; Wang et al., 2011b). Many surface-based morphometry studies describe structural differences at the group level, i.e., between different diagnostic groups. More recently, morphometric maps have also been used to classify individual subjects into diagnostic groups (Ferrarini et al., 2008; Sun et al., 2009a; Kohannim et al., 2010; Wang et al., 2010b; Costafreda et al., 2011). In one study (Sun et al., 2009a), maps of cortical gray matter density achieved 86.1% accuracy in discriminating psychotic patients from control subjects, in leave-one-out tests. In related work (Ferrarini et al., 2008), the notion of biomarker “nodes” was proposed, i.e. regions on surface meshes that contribute most to diagnostic classification; the authors tested their approach on ventricular surface models from Alzheimer’s disease patients and matched controls. Overall, a set of surface-based morphometric features combined with a machine learning algorithm may offer a promising way to improve the performance of computer-assisted diagnostic systems.

An important question for diagnostic classification based on voxel-based or surface-based morphometric maps is which statistics are best to analyze. Statistics derived from anatomical surface models, such as gray matter thickness maps (Thompson et al., 2003; Thompson et al., 2005), radial distances (distances from the medial core to each surface point) (Styner et al., 2004; Thompson et al., 2004a; Carmichael et al., 2006; Carmichael et al., 2007b; a; Carmichael et al., 2007c; Thompson et al., 2007; Chou et al., 2008; Chou et al., 2009; Morra et al., 2009; Apostolova et al., 2010a; Apostolova et al., 2010b; Morra et al., 2010), spherical harmonic analysis (Styner et al., 2005; Gutman et al., 2009), local area differences (related to the determinant of Jacobian matrix) (Davatzikos et al., 1996; Woods, 2003; Chung et al., 2008), Gaussian random fields (Bansal et al., 2007), Reeb graphs (another way to compute radial distances) (Shi et al., 2009) have all been applied to analyze the shape and geometry of various brain structures. Surface tensor-based morphometry (TBM) (Davatzikos et al., 1996; Thompson et al., 2000a; Woods, 2003; Chung et al., 2008) is an intrinsic surface statistic that examines spatial derivatives of the deformation maps that register brains to common templates, and can help to detect subtle differences in local surface morphometry. In recent studies (Wang et al., 2008b; Wang et al., 2009a; Wang et al., 2010c; Wang et al., 2011b), surface multivariate TBM (mTBM) was found to be more sensitive for detecting group differences than other standard TBM-based statistics. As a result, here we decided to use mTBM statistics as the surface statistics to be included in a diagnostic classifier.

Three-dimensional statistical maps can detect consistent local differences in anatomical surfaces. But, when they are applied to classification, the feature dimension is usually much larger than the number of subjects in the sample being analyzed—the “high dimension/small sample size problem”. When a vast number of variables are measured from a small number of subjects, it is often possible to divide the subjects into groups based on the observed features, but the resulting classification rules may generalize poorly to new observations. To select the most useful features, feature reduction can be beneficial. Feature selection approaches are widely used in machine learning, (e.g. (Stearns, 1976; Guyon et al., 2002; Fan et al., 2005; Kuncheva and Rodríguez, 2010)). Even so, most methods still generate very large numbers of features, making it difficult to state intuitively why features are being used to make biological inferences. To address this, sparse learning methods have been proposed to select the most biologically germane features (Tibshirani, 1996; Friedman et al., 2008). Sparse learning methods enjoy strong theoretical properties (Donoho, 2006; Candès and Wakin, 2008) and are receiving increased attention in many application areas (Candès et al., 2006; Figueiredo et al., 2007; Beck and Teboulle, 2009; Wu et al., 2009). Sparse learning has also been applied in neuroimaging to study genetic influences on the brain (Vounou et al., 2010; Hibar et al., 2011; Kohannim et al., 2011; Le Floch et al., 2011; Vounou et al., 2012; Wang et al., 2012a), functional connectivity (Huang et al., 2010; Ryali et al., 2012), and for outcome predictions (Sun et al., 2009a; Shen et al., 2010; Stonnington et al., 2010; Wang et al., 2010a; Wang et al., 2010b; Wang et al., 2011a). In many computer vision, medical imaging and bioinformatics applications, using sparsity as a prior leads to state-of-the-art results (Sun et al., 2009a; Wright et al., 2009; Liu and Ye, 2010a; Liu et al., 2010b).

Here we developed a new approach, based on conformal slit mapping (Wang et al., 2009a), multivariate tensor-based morphometry (mTBM), and sparse learning, to identify cortical biomarkers for classification problems. We hypothesized that mTBM might improve the accuracy for analyzing group differences in neuroimaging data, and for helping individual classification, when used with a sparse learning classifier. We tested our hypothesis on a dataset used in a prior work (Thompson et al., 2005): it consists of 42 subjects with genetically confirmed William syndrome and 40 age-matched controls. The point of using Williams syndrome data as a test is that the diagnosis can be verified using a genetic test. Despite many years of research on brain differences in Williams syndrome - finding differences widely distributed in the brain - no one known trait offers powerful group classification on its own. As such, we chose this dataset as an interesting test case, as it may also identify distinctive cortical features for further study.

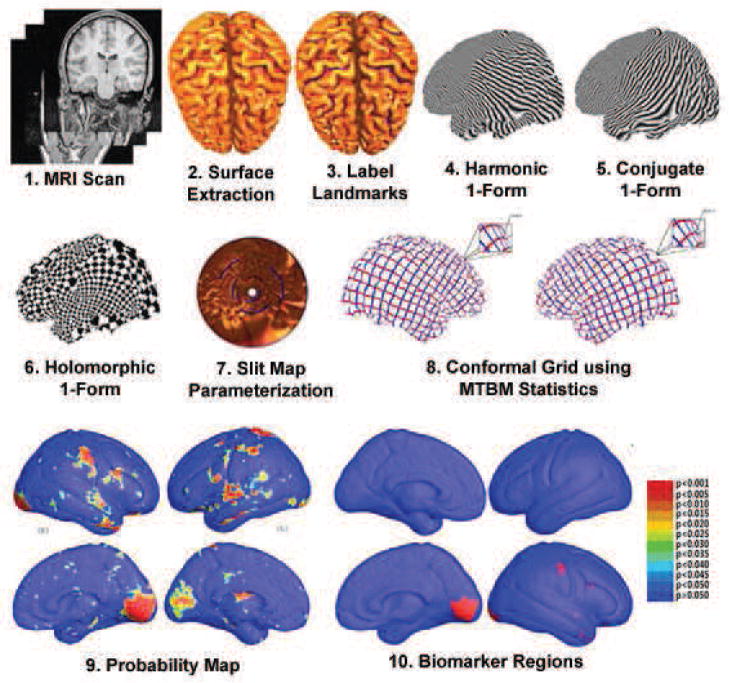
Fig. 1 summarizes the steps we used to analyze cortical surface morphometry. The cortical surface data was from our prior study (Thompson et al., 2005). With 10 selected landmarks on each cortical hemispheric surface, we computed a conformal mapping from a multiply connected mesh to the so-called slit domain, which consists of a canonical rectangle or disk in which 3D curved landmarks on the original surfaces are mapped to parallel lines or concentric slits in the slit domain (Wang et al., 2008a). In this canonical parametric domain, cortical surfaces were matched by a constrained harmonic map (Wang et al., 2007). Multivariate surface statistics were computed from the registered surfaces (Wang et al., 2010c). In one experiment, they were applied to identify regions with significant differences between the two groups. In another experiment, cortical features were fed to a sparse learning method to classify each subject into one of two groups by a leave-one-out test. We also tested other possible surface morphometry statistics to compare them with our multivariate surface statistics. Although the method is illustrated on Williams syndrome data, it is intended to be useful for other disorders as well. Tests on more diverse datasets are reserved for further work.

Figure 1.

A flow chart shows how circular slit map conformal parameterization is used to model cortical surface shapes. The resulting surfaces are analyzed using multivariate tensor-based morphometry and sparse learning methods. After cortical surfaces are extracted from MRI images and landmark curves are labeled either manually or automatically (Thompson et al., 2005), we compute circular slit map conformal parameterizations for each cortical surface, and register surfaces with a constrained harmonic map. The statistics of multivariate TBM are computed at each point on the resulting matching surfaces, revealing regions with systematic anatomical differences between groups. We also apply a sparse learning algorithm to detect some structural features suitable for classification experiments.

2. SUBJECTS AND METHODS

2.1. Subjects

We tested our algorithm on data from a prior study by Thompson et al. (2005). Subjects and brain-scanning protocols were used exactly as in the study by (Reiss et al., 2004; Thompson et al., 2005). Exclusion criteria included a history of medical conditions not typically associated with WS, such as epilepsy or other neurological conditions. All WS participants were evaluated at the Salk Institute (La Jolla, CA) as part of a program project on genetics, neuroanatomy, neurophysiology, and cognition. WS diagnosis was genetically confirmed in all cases by fluorescent in situ hybridization, which tested for deletion of one copy of the elastin gene on chromosome 7. A total of 42 subjects with genetically confirmed Williams syndrome and 40 age-matched healthy controls were included in the study. The studying subject age and sex information is listed in Table 1. Wechsler Full-Scale intelligence quotient (IQ) scores were available for 41 of the 42 WS subjects (mean, 68 ± 9; range, 46–83); the untested subject exhibited similar levels of cognitive function on other measures. As in the earlier studies (Reiss et al., 2004; Thompson et al., 2005), healthy control subjects (with no history of major psychiatric, neurological, or cognitive impairment) were recruited at both the Salk Institute and Stanford University. Control subjects were further screened to rule out any history of learning, language, or behavioral disorder. The majority of controls in the study did not have IQ testing performed. Those that did (n = 16) had a mean full-scale IQ of 104 with an SD of 12 (range, 86 – 126). All procedures were approved by the Institutional Review Boards of both institutions, and all participants provided informed consent (and parents or guardians provided written consent where appropriate). 3D MRI brain images were collected using a GE-Signa 1.5T scanner (General Electric, Milwaukee, MI). The same 3D spoiled gradient echo pulse sequence was used for all participants, with the following parameters: echo time, 5ms; repetition time, 24 ms; flip angle, 45° ; number of excitations, 2; matrix size, 256 × 192; field of view, 24cm; slice thickness, 1.2 mm; 124 contiguous. Scans were analyzed at the University of California Los Angeles Laboratory of Neuroimaging by image analysts blinded to all subject information, including age, gender, and diagnosis (Thompson et al., 2005). All MR images were processed with a series of manual and automated procedures to build brain cortical surfaces and trace landmark curves. The procedure has been described in detail in earlier studies (Thompson et al., 2003; Thompson et al., 2004b; Thompson et al., 2005). In order to extract the brain surfaces, first, non-brain tissue (i.e., scalp, orbits) was removed from the images, and each image volume was re-sliced into a standard orientation by a trained operator who “tagged” 20 standardized anatomical landmarks in each subject’s image dataset that corresponded to the same 20 anatomical landmarks defined on the International Consortium for Brain Mapping-53 average brain (Mazziotta et al., 2001; Thompson et al., 2003; Thompson et al., 2005). Next, a least-squares, rigid-body transformation spatially matched each individual to the average of the healthy control group. In this way, every individual’s brain was matched in space, but global differences in brain size and shape remained intact. Automated tissue segmentation was conducted for each volume dataset to classify voxels as most representative of gray matter, white matter, cerebrospinal fluid (CSF), or a background class (representing extra-cerebral voxels in the image) on the basis of signal intensity. The procedure fits a mixture of Gaussian distributions to the intensities in each image before assigning each voxel to the class with the highest probability (Shattuck et al., 2001). Then each individual’s cortical surface was extracted and three-dimensionally rendered using automated software (MacDonald, 1998). Each resulting cortical surface was represented as a high-resolution mesh of 131,072 surface triangles spanning 65,536 surface points (Thompson et al., 2005). An image analyst, blind to subject diagnosis, gender, and age, traced each of 10 sulci in each hemisphere on each hemisphere surface (Sowell et al., 2003) rendering of each subject’s brain^*.

Table 1.

Subject age, sex information within groups.

	Patients of WS (n=42)	Control (n=40)
Age mean ± SD	29.2 ± 9.0	27.5 ± 7.4
Age range	12–50	18–49
Male/female	19/23	16/24

2.2. Overview of Surface Conformal Slit Mapping

To compute the multivariate statistics, the images need to be registered by an accurate and efficient method, as is also true in the case of more standard morphometric mapping methods, such as voxel based morphometry (VBM) (Ashburner and Friston, 2000) and tensor based morphometry (TBM) (Hua et al., 2012). Thus the first step in our system is to register the brain surfaces from different subjects onto a common template to establish diffeomorphic (one-to-one, smooth) cross-subject correspondences. The surface parameterization process allows us to compare and analyze surface data effectively on a simpler parameter domain, instead of considering the complicated surfaces. A key direction in brain surface registration is to compute a canonical parameter space that can maintain certain properties of the 3D surface, such as geodesics and angles. The conformal slit map (Wang et al., 2008a) method is a numerically stable and efficient method that can induce parametric grids onto surfaces with complicated topologies (multiple boundaries). In this work, we chose slit mapping to construct the canonical parameter space for surface registration. In the Appendix, we briefly explain the mathematical background and implementation details of surface conformal slit mapping.

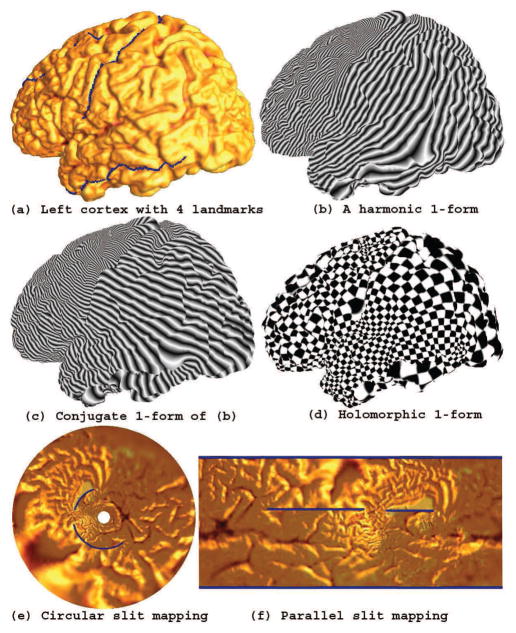
Fig. 2 illustrates the procedure to compute conformal slit mapping on a left hemisphere cortical surface. First, we converted the cortical surface to an open boundary surface by cutting along 4 specific landmark curves. Fig. 2 (a) shows the landmark curves labeled by blue color (the last landmark curve is on the back so it is invisible here). (b) shows a computed exact harmonic 1-form. (c) shows the conjugate 1-form of the exact harmonic 1-form in (b). The final conformal parameterization is illustrated by the texture mapping of the check board image (d). Its circular conformal slit mapping result is shown in (e), where two landmarks were mapped to inner and outer circles while the other two were mapped to two concentric slits. The parallel conformal slit mapping result is shown in (f), where the four landmark curves were mapped to the blue straight lines.

Figure 2. Conformal slit mapping.

After cutting along several landmark curves, we turn a cortical surface to a genus zero open boundary surface (a). By computing the holomorphic 1-form (d), this may then be conformally mapped onto either a circle (e) or a rectangle (f) where the landmarks are mapped to concentric or parallel lines in the slit domain. We then perform nonlinear surface registration in these parameter domains.

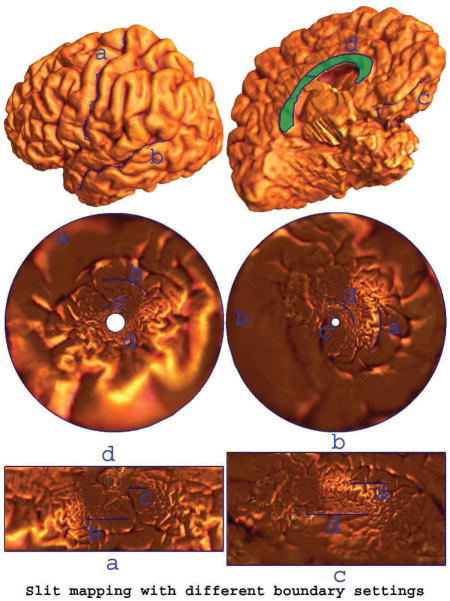
The slit mapping method conformally maps a multiply connected surface to an annulus or a strip with two parallel boundaries. The choice of which boundary is outer is flexible. This flexibility may be useful for selection of the most meaningful conformal parameterization for certain applications. Fig. 3 illustrates a conformal slit mapping result of a left hemisphere cortical surface with 4 boundaries. We selected 5 landmark curves with linking Callosal Sulcus and Inferior Callosal Outline Segment. We cut along the selected landmarks to obtain a genus zero surface with 4 boundaries. In Fig. 3, we show both circular and parallel slit mapping parameterization results while selecting two different pairs of landmark curves as the boundaries in the parameter domains.

Figure 3. Slit mapping with different boundary settings.

For a given cortical surface, we cut it open along 5 selected landmark curves and thus the surface becomes a genus zero surface with 4 open boundaries (first row). The second row shows two circular slit map conformal parameterization results with different landmark curves as outer and inner circular boundaries. The third row shows their parallel slit map conformal parameterization results with different landmark curves as the outer boundaries.

2.3. Surface Registration by Constrained Harmonic Map

Brain surface deformation studies typically require the computation of dense correspondence vector fields to match one brain surface with another. Many brain surface registration methods have been proposed (Fischl et al., 1999; Thompson et al., 2000b; Van Essen et al., 2001; Memoli et al., 2004; Vaillant and Glaunes, 2005; Wang et al., 2005; Qiu and Miller, 2007; Durrleman et al., 2008; Tosun and Prince, 2008; Auzias et al., 2009; Pantazis et al., 2010; Yeo et al., 2010; Zhong and Qiu, 2010). Here we propose to use the slit mapping method to generate a canonical surface to match brain surfaces. Conformal structure is intrinsic to surfaces. As landmark curves have similar geometric positions on different cortical surfaces, the conformal structures of the converted multiply connected components are relatively similar. As a result, their conformal parameterizations to the slit domain are similar to each other.

We propose to compute a direct correspondence between any two surfaces by solving a constrained harmonic map problem (Wang et al., 2007). A harmonic map is one of the most broadly applied methods for registration of computational models of surfaces (Gu et al., 2004; Joshi et al., 2007; Wang et al., 2007). Among its many advantages, the harmonic map (1) measures the elastic energy of the deformation, so it has a clear physical interpretation; (2) can be computed by solving an elliptic partial differential equation, so its computation is numerically stable; and (3) it continuously depends on the boundary condition, so it can be controlled by adjusting the boundary condition. Given two surfaces S₁ and S₂, their conformal slit mappings are τ₁ : S₁ → ℝ² and τ₂ : S₂ → ℝ². We want to compute a map φ : S₁ → S₂. Instead of a direct computation of φ, we can easily find a harmonic map between their parameter domains, i.e. we look for a harmonic map τ: ℝ² → ℝ², such that

$$\tau \circ {\tau }_1(S_1)={\tau }_2(S_2),\tau \circ {\tau }_1(\partial S_1)={\tau }_2(\partial S_2),\mathrm{\Delta }\tau =0.$$ (1)

Then the map φ can be obtained by $\phi ={\tau }_2^{-1}\circ \tau \circ {\tau }_1$. Since τ is a harmonic map while τ₁ and τ₂ are conformal maps, the resulting φ is a harmonic map. With the constrained harmonic map in the slit parameter domain, we are able to obtain exact landmark matching across subjects, which may boost the power of the multivariate statistics.

2.4. Multivariate Tensor-Based Morphometry (mTBM)

To study structural features of the brain, such as cortical gray matter thickness, complexity, and deformation over time, there are two basic approaches: deformation-based morphometry (DBM) (Ashburner et al., 1998; Chung et al., 2001; Chung et al., 2003; Wang et al., 2003) and tensor-based morphometry (TBM) (Davatzikos et al., 1996; Thompson et al., 2000a; Chung et al., 2008). DBM tends to analyze 3D displacement vector fields encoding relative positional differences across subjects, while TBM tends to examine spatial derivatives of the deformation maps registering brains to a common template, constructing morphological tensor maps such as the Jacobian determinant, strain, torsion, or even vorticity.

We used multivariate statistics based on the surface deformation tensors to study cortical surface morphometry (Wang et al., 2010c; Wang et al., 2011b). Suppose φ : S₁ → S₂ is a map from surface S₁ to surface S₂. The derivative map of φ is the linear map between the tangent spaces dφ : TM(p) → TM(φ(p)), induced by the map φ, which also defines the Jacobian matrix of φ. In the triangle mesh surface, the derivative map dφ is approximated by the linear map from one face [v₁, v₂, v₃] to another [w₁, w₂, w₃]. First, we isometrically embed the triangles [v₁, v₂, v₃] and [w₁, w₂, w₃] onto the plane ℝ²; the planar coordinates of the vertices of v_i, w_j are denoted using the same symbols v_i, w_j. Then we explicitly compute the Jacobian matrix for the derivative map dφ (Wang et al., 2008b).

$$d\phi =[w_3-w_1,w_2-w_1]{[v_3-v_1,v_2-v_1]}^{-1}.$$ (2)

In our work, we use multivariate statistics on deformation tensors (Brun et al., 2008; Leporé et al., 2008) and adapt the concept to surface tensors. Let J be the Jacobian matrix and define the deformation tensors as $S={(J^{T}J)}^{\frac{1}{2}}$. Instead of analyzing shape change based on the eigenvalues of the deformation tensor, we consider a new family of metrics, the “Log-Euclidean metrics” (Arsigny et al., 2006). These metrics make computations on tensors easier to perform, as the transformed values form a vector space, and statistical parameters can then be computed easily using standard formulae for Euclidean spaces (Wang et al., 2008b).

To compute group differences with mTBM, we propose to apply Hotelling’s T² test (Hotelling, 1931; Cao and Worsley, 1999; Thirion et al., 2000; Kim et al., 2012) on sets of values in the log-Euclidean space of the deformation tensors. Given two groups of n × 1-dimensional vectors, S_i, i = 1,2, …, p, T_j, j = 1,2, …, q, we use the Mahalanobis distance M to measure the group mean difference,

$$M={(\overline{S}-\overline{T})}^T{\mathrm{\sum }}^{-1}(\overline{S}-\overline{T}).$$ (3)

where S̄ and T̄ are the means of the two groups and Σ is the combined covariance matrix of the two groups (Leporé et al., 2008; Wang et al., 2010c; Wang et al., 2011b). In our study, S and T are the log-Euclidean metrics, e.g. $S_i=log{(J_i^T{J}_i)}^{\frac{1}{2}}$, i = 1,2, …, p and $T_j=log{(J_i^T{J}_j)}^{\frac{1}{2}}$, j = 1,2, …, q.

2.5. Structural Classification Feature Detection with Stability Selection

We used mTBM to detect structural features for group classification (here, i.e. WS vs. controls). For a classification algorithm based on 3D images or surface-based features, the feature dimension is usually much larger than the number of subjects in the sample, so some feature reduction is necessary. There are many feature selection approaches in the data mining literature (Kuncheva and Rodríguez, 2010). One unique challenge for mTBM based feature detection on brain surfaces is the huge dimensionality of the dataset. Therefore, feature selection is performed before the classification process.

Traditionally, feature selection methods, e.g., the recursive feature evaluation method (Guyon et al., 2002; Fan et al., 2005), Sequential Forward Selection (SFS) (Stearns, 1976), are largely based on the discriminative power of each individual variable. However, with huge dimensionality, a feature can gain statistical significance just by pure chance, without having any generalizability to new unseen datasets. In addition, many feature selection algorithms tend to select a vast number of features, which may have no biologically plausible interpretation. To address this problem, we used sparse learning to identify useful features. Sparse signal representation has proven to be an extremely powerful tool for acquiring, representing, and compressing high-dimensional signals (Candès and Tao, 2005; Bruckstein et al., 2009).

For our problem, we consider the dataset d = {(a_i, y_i)|i = 1,2, …, n}, in which a_i is the feature vector, y = ±1 is the class label, and n is the number of samples. For a linear classifier h = aw, we can learn it by solving the following optimization problem:

$${min}_w{\left|\right|Aw-Y\left|\right|}_2^2+\lambda {\mid w\mid }_1.$$ (4)

This procedure is also called the “Lasso” (Tibshirani, 1996), in which λ is the regularization term that balances between sparsity and training error. The only difference between the lasso and the well-known ridge regression (Tikhonov and Arsenin, 1977; Kohannim et al., 2011) is the second term. The ℓ₁-norm regularization will induce an interesting property, i.e., in the solution of the lasso problem, a portion of w will be exactly zero. This provides us a method that will jointly select useful features, and this can be adapted to our high-dimensional problem. After feature selection, the dataset is reduced to a reasonable size and classification is performed. In this stage, we apply ridge regression (Tikhonov and Arsenin, 1977; Kohannim et al., 2011) to discriminate between individuals with WS and healthy controls.

We employed Nesterov’s Accelerated Gradient Method (AGM) to solve the proposed formulation (Eq. 4) (Nesterov, 2007). AGM achieves the optimal convergence rate among all first-order methods (Nesterov, 2007). The core computation for AGM is the proximal operator associated with different regularization Ω(·) (Combettes and Pesquet, 2009). We have developed efficient algorithms to compute the proximal operators in our software package, SLEP (Sparse Learning with Efficient Projections) (Liu et al., 2009). SLEP achieves state-of-the-art performance for many sparse learning models (currently, the package has around 4,000 active users from 17 different countries). The SLEP tools have been applied successfully for stroke prediction (Khosla et al., 2010), craniosynostosis classification (Yang et al., 2011), joint gene expression and network data analysis (Ji et al., 2009; Liu and Ye, 2010b), to predict conversion from mild cognitive impairment (MCI) to AD (Ye et al., 2012), and for brain network analysis in Alzheimer’s disease (Sun et al., 2009b).

To validate the generalization of our model and selected biomarker sets, we changed registering template surfaces and chose stability selection (Meinshausen and Bühlmann, 2010) to select the highest ranking features. Stability selection is a bootstrapping approach to control for false discoveries in the case of finite samples and has been specifically proposed for sparse predictive modeling (Meinshausen and Bühlmann, 2010). The key to stability selection is to perturb the data many times and choose features that occur in a large fraction of the resulting selection sets. Thus, choosing the right value of the regularization parameter λ becomes much less critical and we have a better chance of selecting truly relevant features.

In our experiments, for each feature, we maintain a counting number and put its initial value as 0. The bootstrapping is done on random subsamples of {1, …, n} of size n/2, drawn without replacement. In each step, we solve Eq. 4 and obtain a sparse solution. If a feature is selected, we increase its counting number by 1. After we repeat this procedure s times (e.g. 10,000 times), we obtain a counting number, c_xgi for each feature. We define its selection probability as ${\widehat{\mathrm{\Pi }}}_k^{\lambda }=\frac{c_{{x\text{g}}_i}}{s}$. For a cut-off π_thr(0 < π_thr < 1) and a set of regularization parameters, Λ, the set Ŝ^stable of stable features k is defined by:

$${\widehat{S}}^{\mathit{stable}}=\{k:({max}_{\lambda \in \mathrm{\Lambda }}({\widehat{\mathrm{\Pi }}}_k^{\lambda })\ge {\pi }_{\mathit{thr}})\}$$ (5)

Using this method, we can determine a set of statistical significant features that may be either used for classification or for visualization of some stable feature sets to explain anatomical differences. The stability selection (Meinshausen and Bühlmann, 2010) is appealing in that it has strong theoretical guarantees. Specifically, it has been shown that subsampling/bootstrapping in conjunction with ℓ₁-regularized estimation requires much weaker assumptions on the data for asymptotically consistent feature selection than what is needed for the traditional ℓ₁-regularized scheme. It has been proven to improve estimation of discriminative features significantly, even in cases when the necessary conditions for consistency of the original Lasso method are violated. It has been adopted by some recent brain imaging research work (Ryali et al., 2012; Vounou et al., 2012; Ye et al., 2012).

3. RESULTS

We tested our method on cortical surface data from 42 subjects with genetically confirmed WS and 40 age-matched healthy controls (Thompson et al., 2005). With the slit map method, each cortical surface was conformally mapped to an annulus with concentric arcs. We then computed a constrained harmonic map to register the surfaces to a template surface, using Eq. 1. The template surface was chosen randomly from the control set. The constrained harmonic map helped us build a direct correspondence between the cortical surfaces.

Cortical surface models were cut along 10 landmark curves per hemisphere: the Central Sulcus, Superior Temporal Sulcus (Main Body), Inferior Frontal Sulcus, Middle Frontal Sulcus, Inferior Temporal Sulcus, Secondary Intermediate Sulcus, Transverse Occipital Sulcus, Inferior Callosal Outline Segment, Superior Rostral Sulcus, and Subparietal Sulcus. Landmarks were defined according to a detailed anatomical protocol (Sowell et al., 2002) based on the Ono sulcal atlas (Ono et al., 1990). The written anatomical protocol is available on the internet (Hayashi et al., 2002) and has been used in many published studies. After we cut each cortical surface open along the selected landmark curves, the cortical surface became topologically equivalent to a genus zero surface with 10 boundaries (10 landmark curves). By computing a sequence of differential geometric features on these surfaces - exact harmonic 1-forms, closed harmonic 1-forms, and holomorphic 1-forms - we built a circular slit map, which conformally mapped each surface onto an annulus with 10 boundaries (similar to Fig. 2 (e)). We then matched all surfaces by the constrained harmonic map (Wang et al., 2007). To study surface morphometry, the Jacobian matrices were computed as Eq. 2.

Group Difference Results

We used the Hotelling’s T² test (Hotelling, 1931) to identify between-group differences. Specifically, for each point on the cortical surface, given p=0.05 as the significance level, we ran a permutation test with 10,000 random assignments of subjects to groups to estimate the statistical significance of the areas with group differences in surface morphometry. Fig. 4 shows the significance map of group differences detected between WS and matched control groups, using mTBM as a measure of local surface area and the significance at each surface point to be p=0.05. In Fig. 4, the non-blue colored areas show the areas with (uncorrected) statistically significant differences between the two groups.

Figure 4.

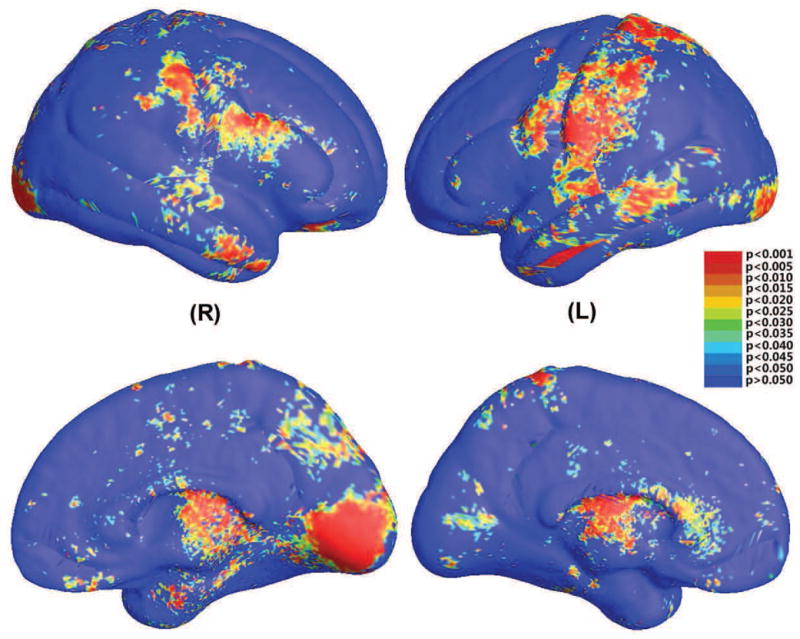
Statistical significance map (uncorrected p-map) shows group differences in regional cortical surface area between 42 WS patients and 40 healthy controls (Thompson et al., 2005). The local statistic analyzed is the multivariate TBM of the cortical parameterization. On the color-coded scale, non-blue colors denote the vertices where there are significant group differences, at the uncorrected p=0.05 level.

The overall significance of the map can be defined as the probability of finding, by chance alone, a statistical map with at least as large a surface area and a statistical threshold more stringent than the predefined level of p=0.05 (note that other methods are also possible, such as those that control the false discovery rate). This omnibus p-value is commonly referred to as the overall significance of the map (or of the features in the map), corrected for multiple comparisons. It basically quantifies the level of surprise in seeing a map with this amount of the surface exceeding a predefined threshold, under the null hypothesis of no systematic group differences. We also computed the overall significance p-values, which were p=0.0004 for the left and p=0.001 for the right hemisphere, respectively.

Classification Results

After we computed the Log-Euclidean metrics to establish a metric on the surface deformation tensors at each point, we applied the ℓ₁-norm penalty (Eq. 4) as the loss function to select sparse features for classification. We used the SLEP package (Liu et al., 2009) for the computation.

In our experiments, we took a cross validation approach to set up free parameters in the Lasso (λ in Eq. 4) and ridge regression method (λ). In our new experiments, in each round of experiments, we divided the training data into four equally sized subsets. Among them, we did cross validation to select the free parameters. Specifically, with a set of selected free parameter values with Lasso and rigid regression classifier, we used three subsets for training and tested the trained classifiers on the last subset. Continue this procedure, each time omitting one subset from the training data and then testing on the omitted one part from the training data and testing on the omitted part. Then the combined 4 part results are put together to estimate the total error rates for the performance comparisons of the free parameter values. We continuously tried all combinations of free parameters and selected the free parameter values by choosing the ones which achieved the best total error rate on the training dataset. Then we applied the chose regularization parameter set to test on the testing dataset.

A leave-one-out method was used to evaluate our classification. First, we randomly removed a sample from the dataset, and set up the free parameter values with a cross validation on the remaining set. From the solution of the Lasso problem, we selected non-zero entries as the useful features. Using only these features, we applied ridge regression to obtain the classifier. Next, the previously removed sample was examined by the classifier. The experiment continued in this leave-one-out fashion, and overall annotation accuracy was calculated at the end. This procedure was repeated 82 times, each time with a different choice for the test data. During the prediction of the ridge regression classifier, instead of the immediate label, a test sample was assigned a score, s, where a positive s value was assigned as WS class or to control (CTL, or typically developing) class. By observing the distribution of the scores for both classes, we can obtain an intuitive impression of the classification power.

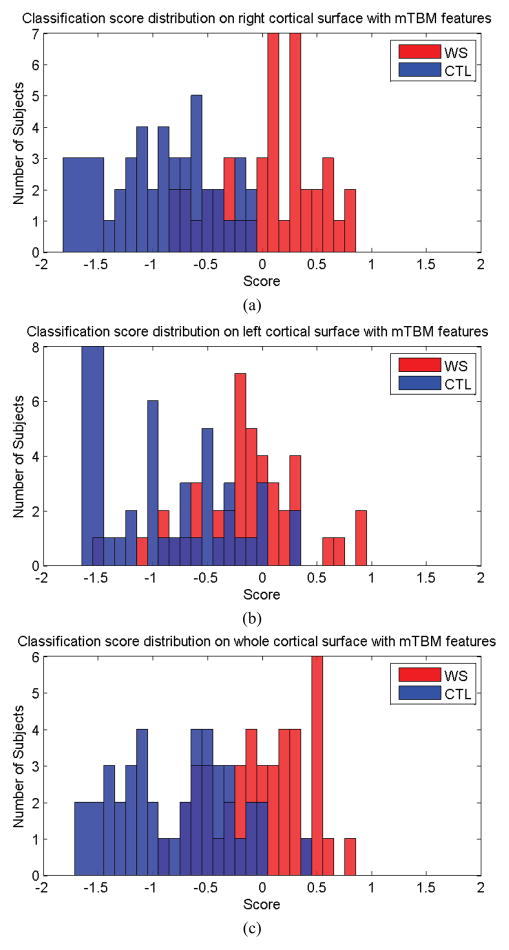
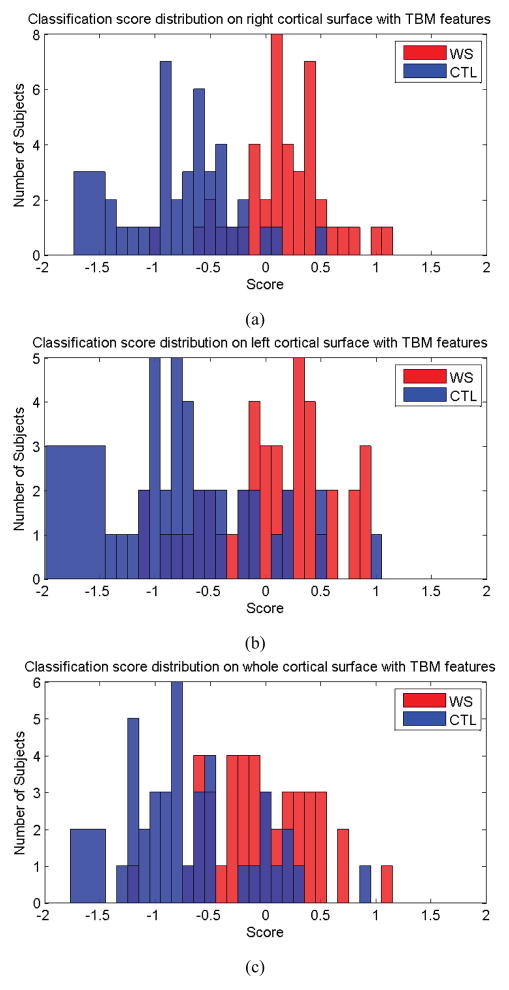
In a series of experiments, the 82 results were used to compute overall performance measures. Fig. 5 shows the classification scores for each subject in the prediction test. Fig. 5 (a) shows the scores for each subject with mTBM features only, on the right cortical hemisphere; in this case, all control subjects were correctly classified while 17 WS patients were incorrectly classified as control subjects. Fig. 5 (b) and (c) show the scores on each subject, with mTBM on the left cortical hemisphere, and using both the left and right cortical hemispheres, respectively.

Figure 5.

Classification scores obtained for both classes, using mTBM on the right hemisphere (a), left hemisphere (b), both left and right hemispheres (c).

The output of each classifier was compared to the ground truth, and a contingency table was computed to indicate the number of particular class labels that were correctly identified as members of one of two classes. The rows of the contingency table represent the true classes and the columns represent the assigned classes. The cell at row r and column c is the number of subjects whose true class is r while their assigned class is c. The possible true- and detected-state combination is shown in Table 2. Four performance measures Sensitivity, Specificity, Positive predictive value, and Negative predictive value were computed as follows:

$$\mathit{Senstivity}=\frac{N_{ww}}{N_{ww}+N_{wc}},\mathit{Specificity}=\frac{N_{cc}}{N_{cw}+N_{cc}},$$

$$\mathit{Positive}\mathit{predictive}\mathit{value}=\frac{N_{ww}}{N_{cw}+N_{ww}},\mathit{Negative}\mathit{predictive}\mathit{value}=\frac{N_{cc}}{N_{wc}+N_{cc}}$$

Table 2.

Possible combinations of ground truth and predicted classifications for two classes. This matrix is used to compute the classifier’s accuracy.

True Class	Assigned Class
	WS	CTL
WS	Nww	Nwc
CTL	Ncw	Ncc

The contingency table for mTBM features is shown in Table 3. Its performance measures are shown in rows 2–4 of Table 8. We can find that the best specificity (100.00%), sensitivity (59.52%), positive predictive value (100.00%) and negative predictive value (70.18%) were achieved when we used mTBM features from the right cortical hemisphere for the training and testing. Consistent with some data from prior WS studies (Thompson et al., 2005), the right half of the brain may contain more diagnostically useful information relevant to WS classification. This assumption is supported by our classification results.

Table 3.

Classification performance with mTBM features on right cortical hemisphere, left cortical hemisphere and both cortical hemispheres.

mTBM on right cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	25	17
	CTL	0	40
mTBM on left cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	15	27
	CTL	2	38
mTBM on both cortical hemispheres	True Class	Assigned Class
		WS	CTL
	WS	21	21
	CTL	1	39

Table 8.

Classification experimental result comparison with various feature groups.

	Sensitivity(%)	Specificity(%)	Positive Value(%)	Negative Value(%)
mTBM on right cortical hemisphere	59.52%	100.00%	100.00%	70.18%
mTBM on left cortical hemisphere	35.71%	95.00%	88.24%	58.46%
mTBM on both cortical hemispheres	50.00%	97.50%	95.45%	65.00%
TBM on right cortical hemisphere	71.43%	92.50%	90.91%	75.51%
TBM on left cortical hemisphere	52.38%	85.00%	78.57%	62.96%
TBM on both cortical hemispheres	42.86%	85.00%	75.00%	58.62%
Pair of EV of J on right cortical hemisphere	52.38%	92.50%	88.00%	64.91%
Pair of EV of J on left cortical hemisphere	50.00%	87.50%	80.77%	62.50%
Pair of EV of J on both cortical hemispheres	42.86%	90.00%	81.82%	60.00%
Volume of both cortical hemispheres	61.90%	52.50%	57.78%	56.76%

Stability Selection for Verification of Feature Sets

In our leave-one-out experiments, we randomly selected a subject as the template and used it to register other surfaces. We used this approach in our prior work (Wang et al., 2009a; Wang et al., 2012b). Our earlier work (Wang et al., 2009b) indicated that it could give rise to different performances to use different surfaces as the registering template. In Wang et al. (2009b), we used surface Ricci flow method to conformally parameterize cortical surfaces. We proposed to use conformal invariants to rank template surfaces and our empirical results showed that it may provide some assistance for template surface selection (Wang et al., 2009b). However, in general it is still challenging to address the optimal registering template selection problem because of the variety of anatomical surfaces. The problem became even more elusive here since conformal invariants proposed in (Wang et al., 2009b) are not computable when we use conformal slit mapping to parameterize cortical surfaces.

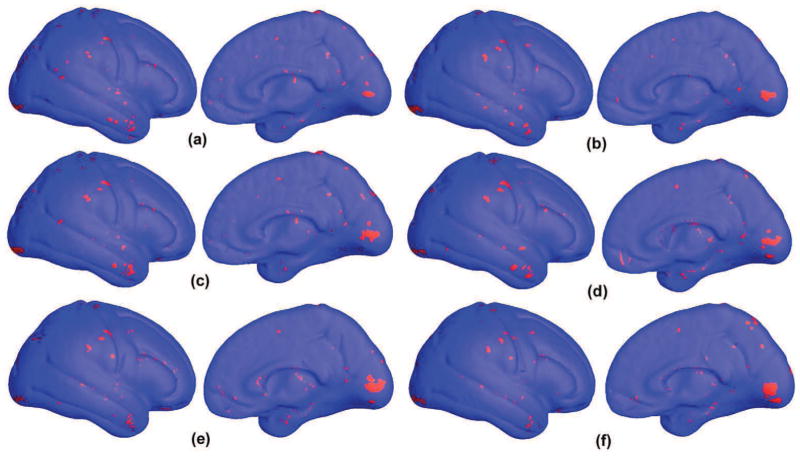
To visualize the selected feature set with different registering template surfaces, here we propose to apply the stability selection to select top features when we use six different cortical surfaces as template for surface registration. Fig. 6 shows the selected top features in these six experiments. The red pixels are selected by the stability selection method as significant features for group discrimination and diagnostic classification at the individual level: a total of 405, 429, 453, 451, 426 and 452 vertices selected in (a), (b), (c), (d), (e) and (f), respectively (π_thr=0.25); (a) is the result with the template surface we used in our leave-one-out cross validation experiments. Since all surfaces are used by the stability selection method, they are not the feature set used in each of the 82 leave-one-out experiments. However, they are a set of statistical significant features that may be used for visualization to help explain anatomical differences. As shown in Fig. 6, the selected vertices are consistent among the six feature sets. This suggests that our method is relatively robust and independent of the particular selection of template surface for surface registration. Although how much a template surface in our surface registration framework affects the final classification results requires careful validation for each application, the current results show our method can select stable feature sets for classification.

Figure 6.

Feature vertices selected by the stability selection method (Meinshausen and Bühlmann, 2010) on the average right hemisphere with three different template cortical surfaces used in the registration step. The red pixels are selected by the stability selection method as significant features for group discrimination and diagnostic classification at the individual level: a total of 405, 429, 453, 451, 426 and 452 vertices selected in (a), (b) (c), (d), (e) and (f), respectively (π_thr =0.25). The selected vertices are relatively consistent among three feature sets. Although more careful validation is needed to explore how the template surface selection affects the final classification results, the current results show our method can select stable feature sets for classification.

Group Difference Comparison between mTBM and Other Surface Morphometry Statistics

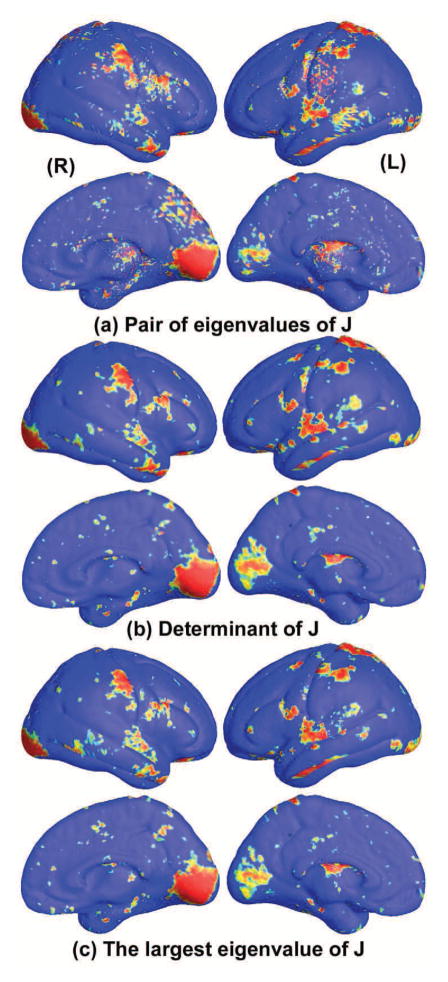
To test the power of multivariate TBM statistics, we also conducted three additional statistical tests based on different tensor-based statistics derived from the Jacobian matrix. The other statistical tests evaluated were: (1) the pair of eigenvalues (EV) of Jacobian (J) matrix, treated as a 2-dimesional vector; (2) the determinant of Jacobian matrix; (3) the largest eigenvalue of Jacobian matrix. For statistics (2) and (3), we applied a Student’s t test to compute the group mean difference at each surface point. In case of statistic (1), we used Hotelling’s T² test to compute the group mean difference. Fig. 7 shows the significance maps of group differences detected between WS and matched control groups, using surface statistics (1)–(3) as a measure of local surface area and the significance at each surface point to be p=0.05. In Fig. 7, the non-blue color areas denoted the statistically significant areas between two groups. In the experiment, all group difference p-maps were corrected using a permutation test with 10,000 random assignments of subjects to groups. In Figs. 4 and 7, we can see that the detected significant areas are consistent for all four statistics. Table 4 gives the permutation corrected p-values comparison.

Figure 7.

Comparison of p-maps for group differences (between Williams syndrome and typically developing participants) with the other three surface statistics.

Table 4.

Permutation test results with four surface statistics.

	mTBM	Pair EV of J	Determinant of J	Largest EV of J
Left hemisphere	0.0004	0.0001	0.0006	0.0009
Right hemisphere	0.001	0.0003	0.0043	0.0033

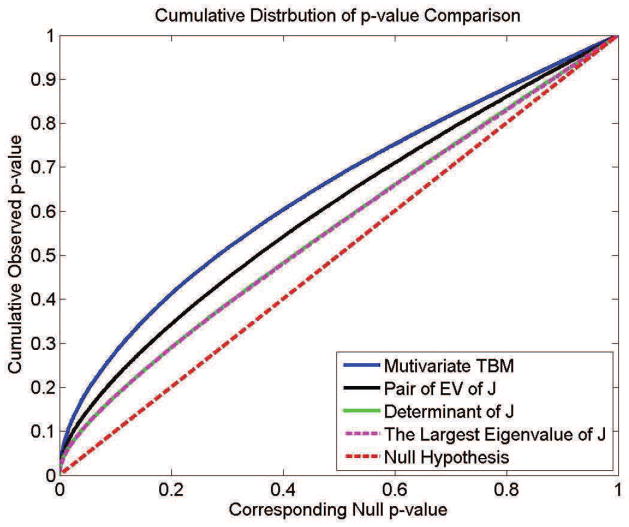
In Fig. 8, the cumulative distribution functions (CDF) of the p-values observed for the contrast of patients versus controls are plotted against the corresponding p-value that would be expected, under the null hypothesis of no group difference, for the different scalar and multivariate statistics. For null distributions, the cumulative distribution of p-values is expected to fall approximately along the line (represented by the dotted line); large deviations from that curve are associated with significant signal, and greater effect sizes represented by larger deviations (the theory of false discovery rates gives formulae for thresholds that control false positives at a known rate). We note that the deviation of the statistics from the null distribution generally increases with the number of parameters included in the multivariate statistics, with statistics on the full tensor typically outperforming scalar summaries of the deformation based on the eigenvalues.

Figure 8.

Comparison of cumulative distribution functions for group differences, using different surface statistics. Based on the FDR method, this type of QQ plot can be used to show if there is aggregate evidence of a signal in a statistical map, across all statistical thresholds.

From Table 4 and Fig. 8, we can see that the mTBM feature (Sec. 2.5) performs better than other two statistics, (2) and (3) - TBM and the largest eigenvalue of Jacobian matrix. Between mTBM and statistic (1), the pair of eigenvalues of Jacobian matrix, we can see that the latter has more significant permutation test results but mTBM has a steeper CDF curve (Fig. 8), i.e. more deviation from the null distribution curve. Considering the pair of eigenvalues is also a kind of multivariate surface statistics, we concluded that generally the multivariate tensor-based morphometry method may be able to detect more surface deformation compared with univariate statistics and produce comparable (or slightly better) results relative to other multivariate statistical approaches.

Classification Performance Comparison with Other Brain Surface features and Volume Features

We also performed additional classification experiments with other features. The features we considered included tensor-based morphometry (TBM) – the determinant of Jacobian matrix (Davatzikos et al., 1996; Thompson et al., 2000a; Woods, 2003; Chung et al., 2008), the pair of eigenvalues of Jacobian matrix and the total volume of both left and right cortical hemispheres. In the first two experiments, we first applied Lasso to select features, and then we used ridge regression to do the classification. To set up the parameters of Lasso and ridge regression, we took the same approach as the one used in mTBM experiments. In each round, we divided the training dataset into four subsets. We performed a cross validation on these four subsets with all possible combinations of the parameter values. The parameter set which achieved the best classification accuracy rates on the training dataset was used as the classifier parameters to classify the last testing dataset. We repeat all the procedure on all data, each time omitting one subset from the training data and then testing on the omitted one part from the training data and testing on the omitted part. Then the final classification results were estimated by combining all leave-one-out experiments. Fig. 9 shows the classification scores for TBM features on right hemisphere (a), left hemisphere (b) and both hemispheres (c). Their contingency tables are shown in Table 5 and their performance metrics are shown in rows 5–7 of Table 8. Fig. 10 shows the classification scores for pair EV of J features on right hemisphere (a), left hemisphere (b) and both hemispheres (c). Its contingency table is shown in Table 6 and its performance metrics are shown in rows 8–10 of Table 8.

Figure 9.

Classification scores obtained for both classes, using TBM features – the determinant of Jacobian matrix (Davatzikos et al., 1996; Thompson et al., 2000a; Woods, 2003; Chung et al., 2008) on the right hemisphere (a), left hemisphere (b), both left and right hemispheres (c).

Table 5.

Classification performance with TBM features (the determinant of Jacobian matrix) on right cortical hemisphere, left cortical hemisphere and both cortical hemispheres.

TBM on right cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	30	12
	CTL	3	37
TBM on left cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	22	20
	CTL	6	34
TBM on both cortical hemispheres	True Class	Assigned Class
		WS	CTL
	WS	18	24
	CTL	6	34

Figure 10.

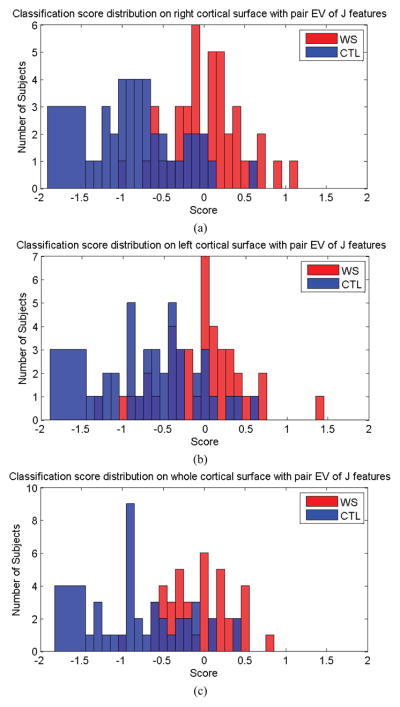
Classification scores obtained for both classes, using the pair of eigenvalues of Jacobian matrix as features for the right hemisphere (a), left hemisphere (b), and for both left and right hemispheres (c).

Fig. 11 shows the classification scores for the cortical volume features. For subject i, we represented its volume as a 2×1 vector, ( $v_l^i,v_r^i$), where $v_l^i$ and $v_r^i$ are the volumes of its left and right hemisphere, respectively. Then we directly applied ordinary least squares (Hastie et al., 2001) for the training and classification. Its contingency table is shown in Table 7 and its performance metrics are shown in row 11 of Table 8.

Figure 11.

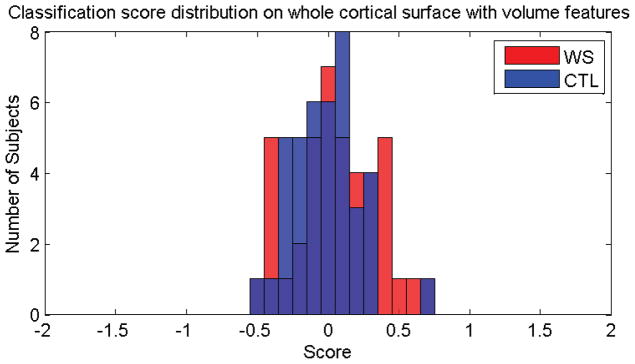
Classification scores obtained for both classes, using the cortical volumes as the features.

Table 7.

Classification performance with total cortical volume features.

TrueClass	Assigned Class
	WS	CTL
WS	26	16
CTL	19	21

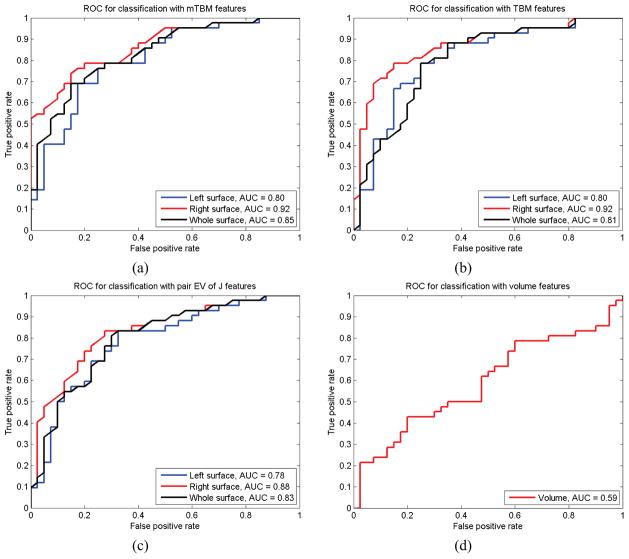
In our experimental results (Table 8), we can find that the best specificity (100%) and positive predictive value (100%) were achieved when we used mTBM features from the right cortical hemisphere for training and testing. The best sensitivity (71.43%) and negative predictive value (75.51%) were achieved when we used TBM features from the right cortical hemisphere for training and testing. To compare performance, we also generated receiver operating characteristic (ROC) curves and computed area-under-the-curve (AUC) measures. In Fig. 12, for the right cortical hemisphere, both mTBM and TBM achieved the best AUC measures (92%), which are better than the results from two other statistical features, i.e., the pair of eigen-values of the Jacobian matrix on the right cortical hemisphere (88%) and cortical volume statistics (59%).

Figure 12.

Classification performance comparison with receiver operating characteristic (ROC) curves and area under curve (AUC) measures. (a)–(d) show results for mTBM, TBM, pair eigen values (EV) of Jacobian matrix and cortical volume statistics, respecitively. With the first three statistics, the results using the right cortical hemisphere only are better than those with left cortical hemisphere and both cortical hemispheres. Among all AUC measures, mTBM on right hemisphere achieved the best performance (AUC=0.94).

4. DISCUSSION

In this paper, our overarching goal was to detect differences in brain surface morphometry. One traditional way to do this is to set up parametric grids on surfaces, and then use differential geometry to come up with useful descriptors of surface features of interest, or to summarize the geometry as a whole. Conformal maps help to induce particularly well-organized grids on surfaces. This simplifies a number of downstream computations of derivatives and metrics. In addition, the surface metric tensor, which is computable from the conformal grid, has a multivariate structure that contains a great deal of information on local surface geometry. Its components cannot simply be inserted into a standard Euclidean multivariate statistical test, as the dependencies among the tensor parameters follow a log-Euclidean law that affects their possible range of values and their statistical distributions. As a result, we end up having to employ the log transform on a matrix, or - more precisely - on a field of matrices or tensors that are defined at the coordinates of the surface grid. The resulting set of surface tensor methods practically encodes a great deal of information that would otherwise be inaccessible, or overlooked. The empirical question is then to see if this extra information is helpful for classification of disease, and if so, under what circumstances.

Our study has two main findings. First, it is possible to detect the subtle difference between or classify people with high accuracy into diseased versus healthy control groups by analyzing surface deformation tensors computed from a set of parametric surfaces using concepts from a limited number of conformal parameterizations. Our current method enforces an exact landmark curve matching on the cortex, using topology optimization. Compared to other cortical surface registration methods based on conformal parameterization, our method eliminates all singular points in the parameterization domains. The analysis of parametric meshes for computational studies of cortical structures can be made more powerful by analyzing the multivariate information inherent in the surface. This type of improvement was shown in group difference analyses. Second, our current experimental results show ℓ₁-norm penalty (sparse learning) methods - that use sparsity as a prior - lead to reasonable classification results. Stability selection method is used to visualize the consistency of selected feature points. The sparsity induced by sparse learning methods may help us to account for biological differences using efficient sets of predictors.

We validated our proposed work in a dataset used in our prior work (Thompson et al., 2005). Our earlier work (Thompson et al., 2005) focused on local surface-based cortical thickness differences, while here we explored more complex surface descriptors related to local surface area and the metric tensor. Although these two approaches might be expected to be highly related, in fact – and perhaps surprisingly – recent work by Winkler and colleagues (2010) shows that the genetic influences on cortical surface thickness and regional cortical volume (which depends on surface area as well as thickness) are almost completely non-overlapping. Although this is somewhat non-intuitive, the genetic factors that drive differences in relative area and cortical thickness seem to be very different. This was established using a quantitative genetic model that separates common and distinct sources of genetic variance. As a result, some biological processes may preferentially affect cortical thickness without greatly affecting the relative areas of parts of the cortex, and vice versa. Our current study demonstrated that it is possible to use only surface morphometry information to achieve group classification, offering a new method to determine when human diseases are associated with characteristic neuroanatomical variation.

Comparison with Two Other Conformal Parameterization Methods

The work reported here used parametric surface approaches to register brain anatomical surfaces (Davatzikos, 1996; Bakircioglu et al., 1999; Thompson et al., 2000b) and, as such, is related to ongoing research by ourselves and others on conformal mapping of brain surfaces. Brain surface parameterization has been studied intensively (Schwartz et al., 1989; Angenent et al., 1999; Timsari and Leahy, 2000; Gu et al., 2004; Hurdal and Stephenson, 2004; Wang et al., 2006; Wang et al., 2007; Wang et al., 2008b; Wang et al., 2008a; Hurdal and Stephenson, 2009; Wang et al., 2012b). Most brain conformal parameterization methods (Angenent et al., 1999; Gu et al., 2004; Hurdal and Stephenson, 2004; Joshi et al., 2004; Ju et al., 2004; Ju et al., 2005; Hurdal and Stephenson, 2009) can handle the complete brain cortex surface, but cannot deal with cortical surfaces that have boundaries. The holomorphic flow segmentation method (Wang et al., 2007) can match cortical surfaces with boundaries or landmarks, but the resulting maps have singularities, which lead to errors in practical applications. Only the Ricci flow (Wang et al., 2006; Wang et al., 2008b; Wang et al., 2012b) and slit map methods (Wang et al., 2008a) can handle surfaces with complicated topologies (boundaries and landmarks) without singularities. The Ricci flow method is a nonlinear optimization process, which is more time-consuming than the slit map method. The Ricci flow method also has higher requirements for the quality of surface tessellations. The slit map method uses a linear approach, which tends to be more efficient and robust. In this paper, the slit map method (Wang et al., 2008a) is used to conformally map a multiply connected domain to an annulus with multiple concentric arcs (called the circular slit map) or to a rectangle with multiple straight lines (called the parallel slit map). It is a global conformal parameterization method without needing the surfaces to be cut up into separate components that are handled individually. Given appropriate boundary conditions, it can compute a unique circular slit map up to a rotation around the center. The slit mapping computes the intrinsic structure of the given surface, which can be reflected in the shape of the target domain. Then the resultant parameterization is used for surface registration.

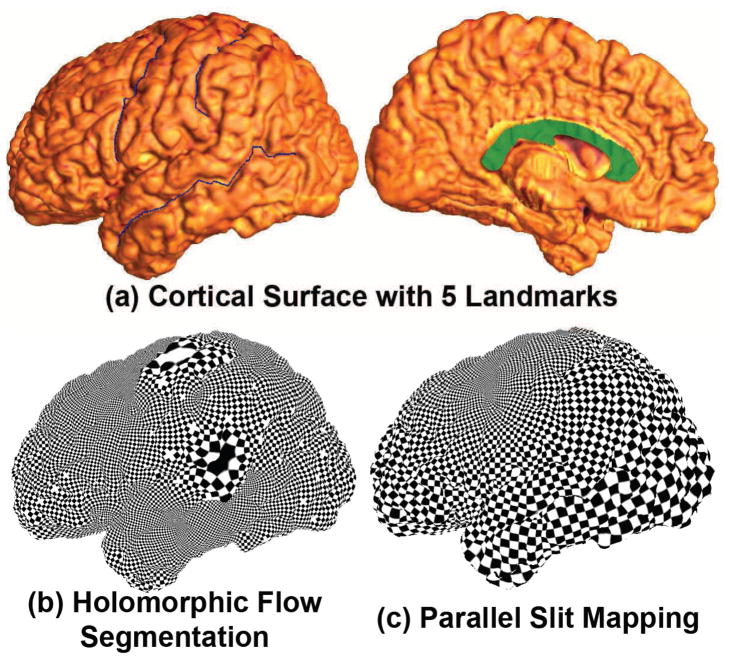
In our work, by cutting along specific landmark curves lying on the cortical surfaces, we convert a cortical surface into a multiply connected surface. We call this topology optimization. With topology optimization, we turn a limited number of important geometric features into boundaries and match them by enforcing the boundary matching conditions (Wang et al., 2008b) or analyze geometric feature statistics around these boundaries (Wang et al., 2009b). Three conformal parameterization methods, the holomorphic flow segmentation method (Wang et al., 2007), the surface Ricci flow method (Wang et al., 2006; Wang et al., 2012b) and the slit mapping method, can parameterize brain cortical surfaces with boundaries, i.e. multiply connected surfaces. Fig. 13 compares two conformal parameterization methods, the holomorphic flow method (Wang et al., 2007) and the parallel slit mapping method. To compute the conformal parameterization, the holomorphic flow method needs to use a “double covering” to turn the surface into a closed surface. The resulting conformal parameterization has singularities which cause big distortions around the singularity areas. Slit mapping works on open boundary surfaces, so that the computational cost is lower. The result does not contain singularities and we also have the flexibility to assign which of two boundaries comprise the outer and inner circles for the circular slit mapping or two outer boundaries for parallel slit mapping. Fig. 13 (a) shows a left hemisphere cortical surface with 5 landmarks: the Precentral Sulcus, Postcentral Sulcus, Superior Temporal Sulcus (Main Body), and linked Callosal Sulcus and Inferior Callosal Outline Segment. The resulting conformal parameterizations are shown by texture mapping of a checkerboard onto the surface. Fig. 13 (b) shows the parameterization result based on holomorphic flow (Wang et al., 2007) and (c) is the parallel slit map. In both pictures, the right angles are preserved but there are two zero points on the holomorphic flow result. However, there is no singularity on the parallel slit mapping result and the parameterization result is relatively uniform over the whole surface. This uniformity is likely to be beneficial for accurate assessment of brain morphometry.

Figure 13.

Comparison of slit mapping to holomorphic flow segmentation, as a method to parameterize the cortical surface. The first row shows a left cortical surface with 5 selected landmark curves. The second row shows results of holomorphic flow segmentation (Wang et al., 2007) and parallel slit mapping. Both algorithms work with surfaces that have boundaries. However the holomorphic flow segmentation method generates singularities in the parameterization results (large tiles in (b)).

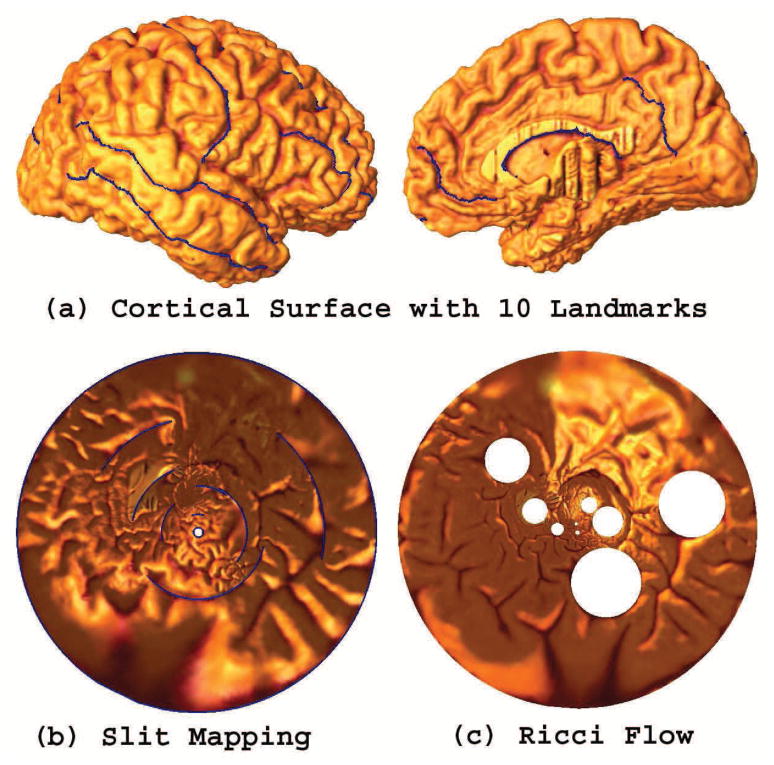
Fig. 14 compares the surface Ricci flow method (Wang et al., 2006; Wang et al., 2012b) and the circular slit mapping method, on a right cerebral cortical surface with 10 landmarks as described in Sec. 3. After cutting along these landmark curves, the cerebral cortical surface is turned into an open boundary surface with 10 boundaries. Ricci flow can also directly work on the multiply connected surface. However, it is a nonlinear optimization process, which is more time-consuming than slit mapping. Slit mapping involves solving a linear system so the computation is easier and stable. The surface with 10 landmarks overlaid is shown in Fig. 14 (a). The respective parameterization results are shown in (b) (circular slit map) and (c) (Ricci flow). Neither result has any singularities, and both of them offer a canonical space for cortical surface registration (Wang et al., 2008b). However, on the unit disk, the single empty hole in the circular slit map occupies 0.07% of the unit disk area while the 9 empty holes in the surface Ricci flow method result occupy 10.46% of the unit disk area. When we use the unit disk for surface parameterization and registration, intuitively, a parameter space without holes is better. When comparing these two unit disk parameterizations for surface mapping, the circular slit mapping result may be more practicable than using surface Ricci flow.

Figure 14.

Comparison of slit mapping with the Ricci flow, as methods to parameterize the cortical surface. The first row shows a right hemisphere cortical surface, with 10 selected landmark curves. The second row shows results of using the circular slit mapping and Ricci flow methods (Wang et al., 2006). Both algorithms work with a surface that has boundaries. However the Ricci flow is computed by solving a nonlinear system, so it is less efficient than the slit map conformal parameterization method.

Stability of Conformal Maps in Longitudinal Scans

The proposed slit map method is based on solving a linear system of differential forms. The differential forms can be easily represented as a vector associated with each edge in our current surface representation. So the method is stable and can be readily extended to a surface with multiple boundaries.

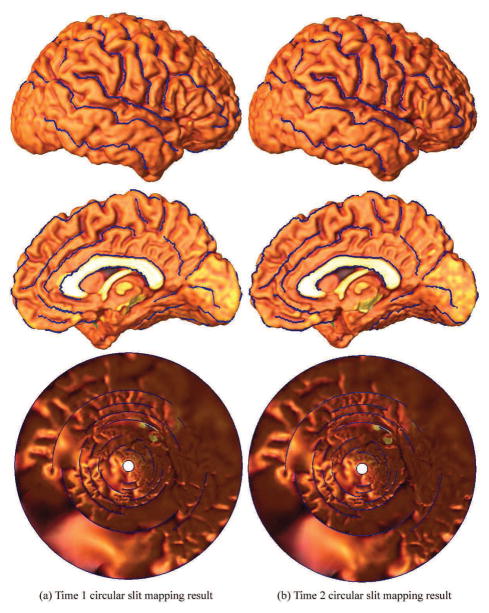
Fig. 15 shows (visually at least) that the parameterization is consistent on a pair of right hemisphere cortical surfaces from the same healthy control subject (Thompson et al., 2003) scanned twice, with a 3.1 years interval. Most of the surface shape was stable with slight differences due to development. In prior work (Thompson et al., 2003), 35 landmark curves were labeled on each cortical surface as detailed in (Sowell et al., 2002) and (Hayashi et al., 2002). The cortical surfaces are shown in Fig. 15, with landmark curves in blue. As an ongoing effort, we are studying the stability of the slit mapping method using different numbers of available landmark curves. Computational results are shown on the last row in Fig. 15. Each cortical surface is conformally mapped to an annulus with 33 concentric slits. We can see that the positions and lengths of the slits are very similar in the two situations. Although more data and computations are clearly necessary, this illustration suggests feasibility and stability of using our conformal slit mapping method, with different number of landmarks.

Figure 15.

Slit mapping on longitudinal cortical surfaces, from the same subject scanned twice. A right hemisphere cortical surface extracted from the same control subject at two different times in our prior study (Thompson et al., 2003). All available landmarks (35 in total) are used as cuts in the surface, allowing the entire surface to be mapped to a unit disk with 33 inner slits and 1 inner circle. The two parameterization results are very similar. Although more empirical data would be useful, this suggests the robustness of our proposed method if a person is re-scanned.

Sulcal landmark curve selection

In our dataset, there are 36 sulcal landmarks on each hemisphere cortical surface and a total of 72 sulcal landmark curves on the whole brain (Hayashi et al., 2002; Sowell et al., 2002). When we initially defined these protocols, 10 years ago, we labeled every possible sulcus from the Ono atlas that could be reliably defined on the brain surfaces of multiple people. A committee of several neurologists and anatomists came up with a protocol that would be feasible for trained anatomists to use reliably, with good inter-rater agreement, even for tracers who had worked independently. In the end, because the protocol was so time consuming to perform, not many investigators were willing to hand-landmark so many curves, even though we did so for this dataset. This motivated us to reduce the total number of sulcal curves used in the registration.

Different studies have historically used different choices of landmark curves. For example, in Pantazis et al. (2010), a set of 26 landmarks was defined per hemisphere while 28 landmark curves were used in Joshi et al. (2012b) and only 14 sulcal curves were used in Zhong and Qiu (2010). In this work, among 36 sulcal landmark curves per hemisphere, we used 10 landmark curves: the Central Sulcus, Superior Temporal Sulcus (Main Body), Inferior Frontal Sulcus, Middle Frontal Sulcus, Inferior Temporal Sulcus, Secondary Intermediate Sulcus, Transverse Occipital Sulcus, Inferior Callosal Outline Segment, Superior Rostral Sulcus, and Subparietal Sulcus. This set of landmarks includes many of the major features of the brain, including landmarks that are scattered across all lobes, especially including the longer sulci. Our experiments on both group difference and classification demonstrated reasonable effectiveness with this selected landmark set. We agree that the current empirical study does not prove that it is the best landmark subset for disease classification, and it would certainly be interesting in the future to optimize the chosen set of landmarks with respect to the classification performance. In the end, one would imagine that classification performance would increase with the number of landmarks chosen, so long as the additional landmarks were in areas that show differences between the groups being classified.

Two-stage Lasso

In our classification experiments, we employed a two-stage approach where Lasso is used to select features and a subsequent ridge regression for the classification. Lasso employs a convex regularization term (ℓ₁-norm) to approximate the combinatorial ℓ₀-norm to make the problem computationally tractable. However, Lasso is known to induce estimation bias due to the convex relaxation; Lasso not only shrinks the coefficients of the irrelevant variables to zero (these features are removed), but also shrinks the coefficients of the relevant variables. In the literature, many methods have been proposed to correct the unnecessary shrinkage, e.g., two-stage Lasso and multi-stage Lasso (Zou, 2006; Zhang, 2010). Since Lasso is reasonably good at identifying relevant features, it is natural to apply a two-stage approach like ours, in which the features are identified at the first stage and the coefficients are learnt at the second stage to reduce the shrinkage effect. It is also common to add a small ℓ₂-norm to the Lasso formulation, which follows the elastic nets formulation (Zou and Hastie, 2005) and overcomes the limitations of the Lasso method. For example, in our SLEP package (Liu et al., 2009), we add a ℓ₂-norm regularization to the Lasso formulation. Our experience showed that it generally improved Lasso performance (Ye et al., 2012).

Leave-N-out Experiments

Besides the leave-one-out experiments, we also performed leave-N-out experiments to help illustrate the mean classification accuracy and its standard deviation when varying the training and testing datasets by random re-sampling. As our current dataset had only 82 subjects, we initially focused on leave-one-out experiments, to maximize the size of the training set. For completeness, we also performed leave-N-out experiments, with mTBM and TBM features, to see how the mean accuracy in a larger test set depended on the test set chosen. In our experiments, for each round, we randomly selected 10 out of 82 images for testing and used the remaining 72 images for training. During training, a cross-validation scheme was adopted to set up the parameter values. The selected parameter values were then applied to test the classifier on the testing data. We further repeated this process 30 times. For each time, an accuracy rate was calculated on the testing dataset. After all rounds of experiments, we obtained a set of accuracy rates from the leave-N-out experiments. We further estimated the mean accuracy rates and their standard deviations. We note that the standard deviation here measures the accuracy on repeated random drawings of 10 subjects from the sample, which were left out from the training set to guarantee independence and avoid circularity. We performed experiments using both TBM and mTBM algorithms and their experimental results (mean accuracies and standard deviations) are summarized in Table 9.

Table 9.

Mean accuracy and standard deviation results for leave-N-out experiments with mTBM and TBM. Results are shown for two-sample t-tests that test whether the difference between the two average accuracy rates is statistically different. These results are shown as p-values in the last column of the table. Interestingly, the multivariate TBM method does not outperform the standard TBM method applied to surfaces.

	mTBM	TBM	p-value
Left hemisphere	0.66 ± 0.150	0.68 ± 0.161	0.62
Right hemisphere	0.76 ± 0.113	0.77 ± 0.123	0.66
Whole brain	0.68 ± 0.130	0.65 ± 0.125	0.32

In line with the leave-one-out experiments – right hemisphere features tended to perform better in discriminating the two classes (2 sample t-test, right vs. left, p=0.0051; right vs. whole, p=0.0136). As seen from the standard deviations, the classification accuracy rate did not have a wide range. We computed 30 accuracy rates using different training/testing partitions, but none of the comparisons was significant. Surprisingly perhaps, the multivariate TBM method did not outperform the standard method. This may be due to the relatively small size of the current dataset. It could be that the benefit of learning of the multivariate parameters in TBM is either minimal, or requires a very large sample size to detect.

Group Difference Performance vs. Classification Performance

Overall, these leave-one-out experiments correctly classified 67/82 cases for TBM and 65/82 cases for mTBM. A binomial proportion test can be performed on these two proportions, with the null hypothesis that these two accuracy rates are the same. The p-value from this test was 0.6935, which shows that no one method had statistically superior accuracy. While mTBM achieved the strongest group difference, when compared to three other TBM-based and volume features, it achieved classification accuracy comparable to univariate TBM.

Based on the results, we have demonstrated that MRI-based disease classification can benefit from surface parameterization with differential forms and tensor-based morphometry, in the log-Euclidean domain, on the resulting surface tensors. The similar classification performance of mTBM and TBM may be due to the limited sample size for the dataset used in our current experiments, although we know that 82 subjects is an adequately powered dataset to detect group differences, as we were able to detect them. It could be that multivariate surface descriptors require a larger sample size to show benefits over the scalar descriptors in classification accuracy, to more accurately learn their covariance structure. Or, it may be that multivariate TBM can outperform scalar TBM in some contexts but not others, or in some diseases but not others, depending on the type of surface differences there are. A strong group difference result does not always guarantee a better classification power; this is consistent with discoveries reported in some prior work (Lao et al., 2004; Chincarini et al., 2011; Cuingnet et al., 2011). Our longer-term goal is to investigate how to best apply surface tensor-based morphometry (Davatzikos et al., 1996; Thompson et al., 2000a; Woods, 2003; Chung et al., 2008; Wang et al., 2010c) in disease classification research.

Improvement of classification performance with spatial and anatomical regularization

Our current work proposed a surface-based framework which demonstrated that, by analyzing the full surface deformation tensors computed from a set of parametric surfaces, one may achieve improved group difference detection and group classification performance. In our experiments, with the ℓ₁-norm penalty (sparse learning) methods, we achieved reasonable classification results. However, there is a potential to further improve classification performance by considering spatial and anatomical regularization in medical imaging research. Pioneering work has demonstrated that spatial and anatomical information can enhance performance of typical classifiers, such as support vector machine (SVM) (Fung and Stoeckel, 2007; Cuingnet et al., 2010), Adaboost (Xiang et al., 2009) and Bayesian classifier (Sabuncu and Van Leemput, 2011), improve feature reduction efficiency (Batmanghelich et al., 2012) and behavior prediction accuracy (Michel et al., 2011). The key insight is that the underlying anatomical structures are smooth, i.e. features in biomedical applications exhibit certain intrinsic structures, such as groups, graphs, and trees (Jacob et al., 2009; Li and Li, 2010; Liu and Ye, 2010b; Liu et al., 2010a; Liu and Ye, 2010a); for example, if a surface point shows significant difference between two groups, most likely its neighboring surface points also have certain statistical discrimination power. More importantly, a single surface point may not carry strong statistical power of its own, but a set of such correlated points may do so. In other words, an association mapping approach may “borrow strength” from correlated phenotypes and can potentially yield higher statistical power (Ferreira and Purcell, 2009). Recently, we and other groups have developed structured sparse learning formulations which incorporate the complex feature structures into the sparse learning model; they have been applied successfully in many applications including computer vision, medical imaging and bioinformatics (Zou and Hastie, 2005; Yuan and Lin, 2006; Jacob et al., 2009; Zhao et al., 2009; Kim and Xing, 2010; Li and Li, 2010; Liu and Ye, 2010b; Liu et al., 2010a; Liu and Ye, 2010a; Wang et al., 2011a; Wang et al., 2012a). In future, we plan to develop advanced structured sparse learning strategies for surface-based disease marker identification with the potential of leading to major discoveries in neuroimaging.

Alternatives for full deformation tensor information processing

In our work, we analyzed full deformation tensor information by using log-Euclidean framework. However, there are other ways available to analyze the full tensor information. A simple strategy is to directly use a Euclidean structure on square matrices to define a metric on the tensor space. But the classical Euclidean framework has many defects, for example, null or negative eigenvalues appear during Euclidean computation. To fully circumvent these difficulties, affine-invariant Riemannian metrics have been proposed for tensors (Fletcher and Joshi, 2004; Moakher, 2005; Pennec et al., 2006) and a class of tensor interpolation paths, geodesic-loxodrome (Kindlmann et al., 2007), was proposed to explicitly preserve clinically important tensor attributes. While the log-Euclidean framework is the most computationally convenient, other approaches (Fletcher and Joshi, 2004; Moakher, 2005; Pennec et al., 2006; Kindlmann et al., 2007) also provide valid, theoretically rigorous alternatives for full anatomical deformation tensor analysis.

Beyond the current system

In this paper, we validated our proposed work in a dataset used in our prior work (Thompson et al., 2005). In Thompson et al. (2005), an operator who was blind to the subject’s pathological condition has normalized identified certain landmark points. In this scenario, when a new subject was given to the system, the operator identified a set of landmark points using the International Consortium for Brain Mapping-53 average brain (Mazziotta et al., 2001; Thompson et al., 2005). The identified landmark points were used to compute a rigid-body transformation that aligns brain volume images in a standard space for segmentation and cortical surface generation. The generated surfaces and 10 manually labeled landmark curves on the surfaces were the input to our method to apply multivariate statistics for analyzing the group difference and classification. However, our method is general enough to process landmark curves that are either manually traced or automatically detected by some other software tools. We are exploring the possibility to take the landmark curves detected by BrainSuite (Joshi et al., 2012a) as input for conformal slit map based surface registration. Our ongoing work (An et al., 2012) also tries to apply multivariate tensor-based morphometry on cortical surface built by FreeSurfer (Fischl et al., 1999).

5. CONCLUSION

We presented an MRI-based computer-assisted diagnostic classification system that finds vertices and local features on cortical surface models to best discriminate two groups of subjects. Our system was based on mTBM and sparse learning, with the ℓ₁-norm based penalty. The mTBM captured the full deformation tensor information and performed better than TBM (the determinant of Jacobian matrix) in both group difference and classification studies. The sparse learning method selected a smaller, biologically plausible feature set, consistent with prior knowledge of cortical anomalies features in WS. In leave-one-out tests, with the same parameter settings, our surface-based method achieved better classification results than those using the pair of eigenvalues of Jacobian matrix and the whole cortical volumes as features. Ongoing work is testing this framework for studying structural imaging biomarkers of other disorders, such as Alzheimer’s disease.

Table 6.

Classification performance with pair of eigenvalues of Jacobian matrix on right cortical hemisphere, left cortical hemisphere and both cortical hemispheres.

Pair EV of J on right cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	22	20
	CTL	3	37
Pair EV of J on left cortical hemisphere	True Class	Assigned Class
		WS	CTL
	WS	21	21
	CTL	5	35
Pair EV of J on both cortical hemispheres	True Class	Assigned Class
		WS	CTL
	WS	18	24
	CTL	4	36

APPENDIX

The following sections describe the mathematics underlying the slit mapping algorithm and how we measure features on the cortical surfaces. Some concepts come from exterior calculus and use the terminology of differential forms, which is useful for analyzing surfaces represented as parametric meshes.

A.1. Theoretic background on holomorphic 1-forms

Suppose S is a surface embedded in ℝ³, with induced Riemannian metric g. S is covered by an atlas {(U, φ)}. Let (x, y) be the local parameter on the chart (U, φ). If the metric g has the representation g = e^2λ(x,y) (dx² + dy²), we say (x, y) is isothermal. An atlas consisting of isothermal parameter charts is called a conformal structure.

The Laplace-Beltrami operator on a surface is defined as

$${\mathrm{\Delta }}_{\mathbf{g}}=\frac{1}{e^{2\lambda (x,y)}}\left(\frac{\partial }{\partial x^2}+\frac{\partial }{\partial y^2}\right).$$ (6)

A function defined on a surface f : S → ℝ is harmonic, if Δ_gf ≡ 0.

Mathematically, the differential form is a concept used in multivariable calculus that is independent of any chosen set of coordinates - it has many applications in geometry, topology and physics. The general setting for the study of differential forms is on a differential manifold. A differential 1-form in the local parameters (x, y) may be defined as

$$\omega =f(x,y)dx+g(x,y)dy.$$ (7)

where f, g are smooth functions. Differential 1-forms are naturally dual to vector fields on a manifold. The algebra of differential forms along with the exterior derivative defined on it is preserved under smooth functions between two manifolds. Specifically, ω is a closed 1-form, if in each local parameter (x, y), $\frac{\partial f}{\partial y}-\frac{\partial g}{\partial x}=0$. If ω is the gradient of another function defined on S, it can be called an exact 1-form. An exact 1-form is also a closed 1-form. If a closed 1-form ω satisfies $\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}=0$, then it is a harmonic 1-form. The gradient of a harmonic function is an exact harmonic 1-form.

The Hodge star operator acting on a differential 1-form gives the conjugate differential 1-form

$${}^{\ast }\omega =-g(x,y)dx+f(x,y)dy.$$ (8)

Intuitively, the conjugate 1-form *ω is obtained by rotating ω by a right angle everywhere. If ω is harmonic, so is its conjugate *ω.

Built upon the harmonic 1-form concept, the holomorphic 1-form is a differential form on a manifold which can have complex coefficients. It consists of a pair of conjugate harmonic 1-forms

$$\tau =\omega +{\sqrt{-1}}^{\ast }\omega .$$ (9)

If two harmonic fields are orthogonal everywhere, they form a holomorphic 1-form. An intrinsic way to compute conformal parameterization is to search for a holomorphic 1-form that satisfies certain properties. In conformal slit mapping, we shall find certain holomorphic 1-forms with special behavior on the boundaries of the surface.

Suppose S is an open surface with n boundaries γ₁, γ₂, … γ_n, we can uniquely find a holomorphic 1-form τ, such that (Ahlfors, 1953)

$${\int }_{{\gamma }_k}\tau =\{\begin{array}{ll}2\pi \hfill & k=1\hfill \\ -2\pi \hfill & k=2.\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (10)

Definition 1 (Circular Slit Mapping)

Fix a point p₀ on the surface S, for any point p ∈ S, let γ be an arbitrary path connecting p₀ and p, then the circular slit mapping is defined as φ(p) = e^∫_γτ.

Theorem 1

The function φ effects a one-to-one conformal mapping of surface S onto the annulus 1 < |z| < e^λ₀−n − 2 concentric arcs situated on the circles |z| = e^λ_i, i = 1,2, … n − 2.

The proof of the above theorem on slit mapping may be found in (Ahlfors, 1953). For a given choice of the inner and outer circle, the circular slit mapping is uniquely determined up to a rotation around the center. The parallel slit mapping can be defined in a similar way.

Definition 2 (Parallel Slit Mapping)

Let S̄ be the universal covering space of the surface S, π : S̄ → S be the projection and τ̄ = π*τ be the pull back of τ. Fix a point p̄₀ on S̄, for any point p̄ ∈ S, let γ̄ be an arbitrary path connecting p̄₀ and p̄, then the parallel slit mapping is defined as φ̄(p̄) = ∫_γ̄τ̄.

In our work, we employ the concepts of holomorphic 1-form and conformal slit mapping to compute a conformal parameterization of cortical surfaces. On the Euclidean parameter domain, the constrained harmonic map is computed to construct correspondences between cortical surfaces.

A.2. Computation of Surface Conformal Slit Mapping

In engineering fields, smooth surfaces are often approximated by simplicial complexes (triangle meshes). Major concepts in the continuous setting can be generalized to the discrete setting. In this section, we briefly describe the algorithm implementation to compute the 1-forms and slit mapping.

Suppose M is a triangle mesh with n +1 boundaries, denoted as ∂M = γ₀ – γ₁ –··· – γ_n. We use v_i to denote a vertex, which is also a 3D coordinate vector, [v_i, v_j] denote an edge connecting vertices v_i and v_j, [v_i, v_j, v_k] denote a triangle formed by vertices v_i, v_j, and v_k. The angle at vertex v_i in triangle [v_i, v_j, v_k] is denoted as ${\theta }_{jk}^i$. The discrete functions defined on vertices, edges, and faces are called discrete 0-forms, 1-forms, and 2-forms, respectively. The discrete divergence, discrete Laplace-Beltrami operator and discrete wedge operator can be defined as reported in our prior work (Wang et al., 2008a; Wang et al., 2010c).

The algorithm pipeline is as follows:

1. Compute the basis for all exact harmonic 1-forms;

2. Compute the basis for all harmonic 1-forms;

3. Compute the basis for all holomorphic 1-forms;

4. Construct the slit mapping.

The detailed algorithms to compute 1-forms are reported in our earlier work (Wang et al., 2008a; Wang et al., 2010c). Here we give a brief description of the pipeline implementation. Without loss of generality, we map the boundary γ₀ to the outer circle of the circular slit domain, γ₁ to the inner circle and all other boundaries to the concentric slits. Briefly, first, for each inner boundary γ₁, … γ_n, a harmonic function is computed by solving a Dirichlet problem (Wang et al., 2008a; Wang et al., 2010c). By definition, the exact harmonic 1-form ω_k can be computed as the gradient of the harmonic function on boundary γ_k, (k = 1, 2, …, n). We denote the exact harmonic 1-forms basis as {ω₁, ω₂, …, ω_n}. Second, we compute the closed but non-exact harmonic 1-form τ_k along the path connecting the inner boundary γ_k, (k = 1, 2, … n) to outer boundary γ₀ (Wang et al., 2008a; Wang et al., 2010c). The closed harmonic 1-form basis is the union of the exact harmonic 1-forms basis {ω₁, ω₂, …, ω_n} and the closed but non-exact harmonic 1-forms basis {τ₁, τ₂, …, τ_n}. The computed closed harmonic 1-forms basis is used to improve the computational accuracy of the conjugate 1-form *ω_k of the exact harmonic 1-form ω_k because of the inaccuracy of directly applying the brute-force Hodge star operator (Eq. 8). We denote the conjugate 1-forms basis as {*ω₁, *ω₂, …, *ω_n} (Wang et al., 2008a; Wang et al., 2010c). Then, the holomorphic 1-forms basis is { ${\omega }_1+{\sqrt{-1}}^{\ast }{\omega }_1,\dots ,{\omega }_n+{\sqrt{-1}}^{\ast }{\omega }_n$} (Eq. 9). Next, for surface conformal slit mapping, we need to find a special holomorphic 1-form $\omega ={\sum }_{i=1}^n{\lambda }_i({\omega }_i+{\sqrt{-1}}^{\ast }{\omega }_i)$, such that the imaginary part of its integral satisfies

$$Im\left({\int }_{{\gamma }_k}\omega \right)=\{\begin{array}{ll}-2\pi \hfill & k=1\hfill \\ 0\hfill & k>1\hfill \end{array}.$$ (11)

To get the coefficients λ_i, we solve the following linear system for λ_i, i = 1,2, …, n:

$$\left(\begin{array}{cccc}{\alpha }_{11}& {\alpha }_{12}& \cdots & {\alpha }_{1n}\\ {\alpha }_{21}& {\alpha }_{22}& \cdots & {\alpha }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\alpha }_{n1}& {\alpha }_{n2}& \cdots & {\alpha }_{nn}\end{array}\right)\left(\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ ⋮\\ {\lambda }_n\end{array}\right)=\left(\begin{array}{c}-2\pi \\ 0\\ ⋮\\ 0\end{array}\right).$$ (12)

where α_jk = ∫_γj*ω_k.7

It can be proved that this linear system has a unique solution, which reflects the fact that γ₁ is mapped to the inner circle of the circular slit domain. Further, the system implies λ₁α₀₁ + λ₂α₀₂ + … + λ_nα_0n = 2π, which means that γ₀ is mapped to the outer circle in the circular slit domain. The circular slit mapping is a complex-valued function φ : M → ℂ. Choosing a base vertex v₀ arbitrarily, and for each vertex v ∈ M choosing the shortest path γ from v₀ to v, the map can be computed as φ(v) = e^∫_γω. Based on the circular slit map φ, we can compute a parallel slit map φ : M → ℂ as φ(v) = lnφ(v).